基于数学核心素养的不等式教学探析

福建省龙岩一中 (364000) 方秦金

“数学核心素养”是当下的热词.何为数学核心素养，《普通高中数学课程标准》(征求意见稿)提出数学的核心素养是学生应具备的能够适应终身发展和社会发展需要的，与数学有关的关键能力和思维品质.提出数学教育的终极目标：用数学的眼光观察现实世界、用数学的思维分析现实世界、用数学的语言表达现实世界.具体为六大核心素养，即数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.

如何培养数学核心素养是新形势下教育教学的重要问题，本文以不等式的教学为例阐述培养数学核心素养的途径与方法，供参考.

1.突出基础与记忆

数学基础知识和基本技能是数学核心素养形成的基础.“万丈高楼平地起”， 数学核心素养是基础知识、基本技能、数学思考、数学态度等的综合体现，数学核心素养总是基于数学的知识与技能来实现的，没有扎实的基础就失去了继续前进的基石与动力.如何突出基础呢？

(1)重视基础知识的前后联系

在讲不等式性质时可复习已学过的不等式性质：

不等式两边加(或减)同一个数(或式子)，不等式的方向不变；

不等式两边乘(或除以)同一个正数，不等式的方向不变；

不等式两边乘(或除以)同一个负数，不等式的方向改变；

在讲一元二次不等式及其解法时可复习初中一元一次不等式的解法.

如此等等，在知识的前后联系中数学的系统性与逻辑性得以加强.

(2)重视定理与性质的推导及基本解题方法的记忆

数学是建立在定理与性质之上的一套逻辑系统.公式的推导、定理的证明，不仅有利于理解与掌握定理和公式、理解公式之间的相互关系，还有利于培养逻辑推理能力，从而培养数学核心素养.另外数学基本解题方法的记忆对数学核心素养的形成也极为重要，没有记忆就没有思维，也就无法生成素养！

例1a,b,c为实数，证明：a2+b2+c2≥ab+ac+bc.

法二：(综合法)∵a2+b2≥2ab,c2+b2≥2cb,a2+c2≥2ac,三式相加便得a2+b2+c2≥ab+ac+bc.

法三：(构造函数法)设f(x)=x2-(b+c)x+b2+c2-bc,可知判别式Δ≤0，故f(a)≥0，得证a2+b2+c2≥ab+ac+bc.

讲完这题后可叫学生做下面的练习.

a,b,c为正实数，证明：a3+b3+c3≥3abc.

面对题目不少优秀学生都眉头紧皱，事实上利用前面的三种方法均可.

法二：(综合法)a3+b3+c3+abc-abc≥

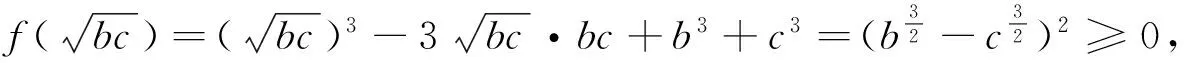
有了这些基本解题方法的记忆与训练，较难的题也会有思路了.

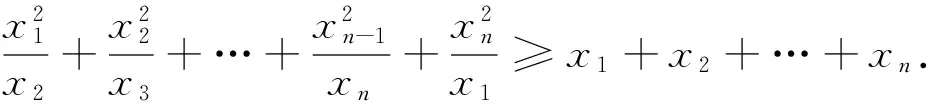
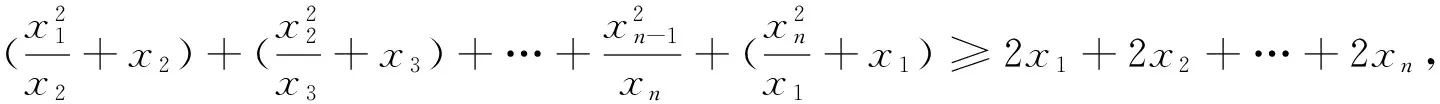
2.重视能力与思维

数学能力是指个体迅速、成功地完成数学活动(数学学习活动、数学研究活动)的一种稳定的个性特征.逻辑思维能力体现了数学能力的典型特征，在数学中它表现为用数和符号来进行思维活动的能力，具有较高的抽象水平和较高的心智活动标准.

《现代汉语词典》对“思维”的解释是：在表象、概念的基础上进行分析、综合、判断、推理等认识活动的过程，是人脑对客观事物的间接和概括的反映.如何提升能力与发展思维呢？

(1)在注重理解中提升能力

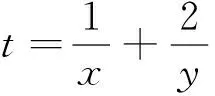
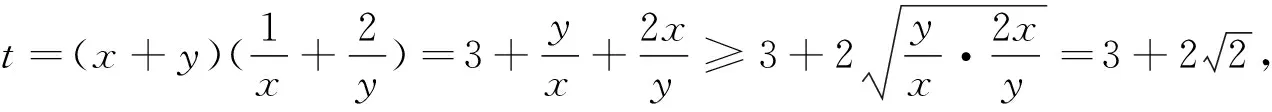
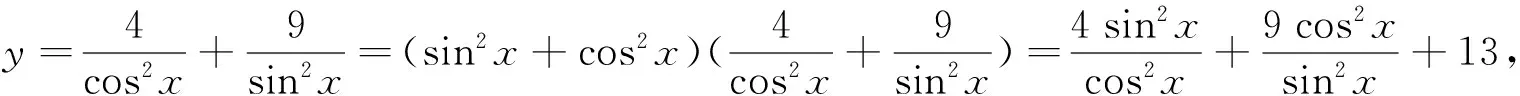
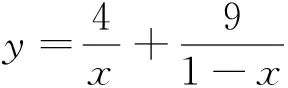
(2)在解题障碍突破中发展思维

数学学习离不开解题，解题也常常会碰到障碍.善于突破、敢于突破解题障碍是发展思维的有效途径.不等式问题的解题障碍常常源于不等式问题考查的交汇性与隐蔽性.

如2014年高考新课标全国卷Ⅱ理科第17题： 已知数列{an}满足a1=1，an+1=3an+1.

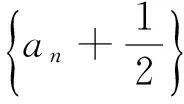
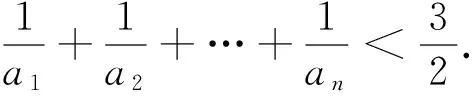
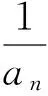
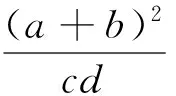
A.0B.1C.2D.4

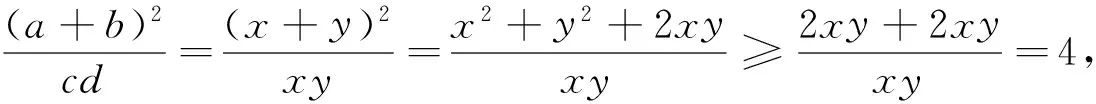
3.注重变式教学

变式教学是指在教学过程中通过变更概念非本质的特征、改变问题的条件或结论、转换问题的形式或内容，有意识、有目的地引导学生从“变”的现象中发现“不变”的本质，从“不变”的本质中探究 “变”的规律的一种教学方式.变式教学有利于揭示问题的本质，有利于思维灵活性的培养，从而培养数学核心素养.

(1)重视课本例题与习题的变式

变式不难，只要养成了变式的习惯可以说变式是无处不在、随心所欲的.如在讲了人教A版必修5P78的例：求不等式4x2-4x+1>0的解集后可作以下变式：

变式1 解不等式：4x2-x-3>0;

变式2 解不等式：4x2-|x|-3>0;

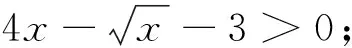
变式4 解不等式：4x2-x-3≥0;

变式5 解不等式：4x2-x-3<0;

变式6 解不等式:x2-(a+1)x+a>0;

变式7 解不等式：ax2-(a+1)x+1<0;

……

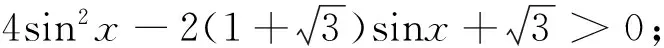
通过变式训练，一元二次不等式各类型的解法及其注意点都清楚了.

(2)重视学生自觉变式能力与意识的培养

老师课堂讲授中的变式有利于问题本质的揭示与把握，但学生解题思维灵活性与深刻性的培养最终还有赖于学生在解题中的自觉变式，如果把变式看成是折腾的话，学会自我折腾方能不受折腾，感受解题的乐趣、提高解题的能力.

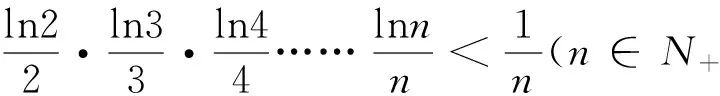
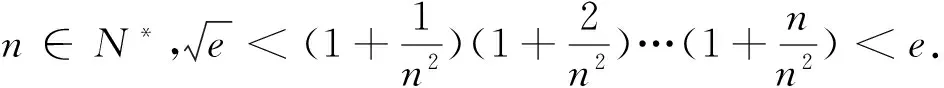
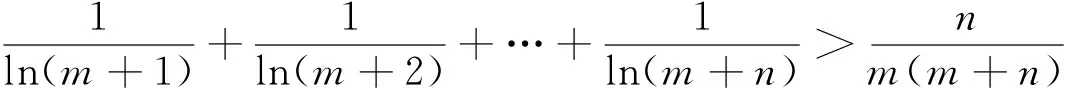
在老师引导下的变式与自觉变式的训练中，思维的灵活性及深刻性得到培养，对问题本质的把握得以不断实现.

4.尝试师生互动教学模式

在课堂教学中教师起主导作用，但课堂归根到底是学生的，只有学生在课堂中积极参与并获得发展才能保证教学的有效性，基于不等式内容的灵活性与综合性，可尝试以下两种互动教学模式.

(1)让学生讲

学生讲有利于生生互动、师生互动，有利于学生思维的严密性培养.

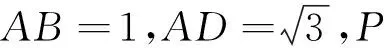
评析：这题答案是B，我校的得分率是44%，我让一同学讲解，他先讲了自己的思考，而后结合其他同学的思路从不同的角度得出了多种解法.

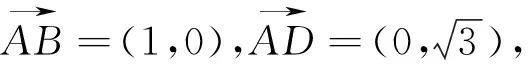
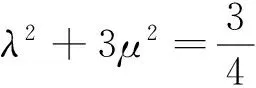
(2)让学生探究

探究是指学生在学习情境中通过阅读、观察，发现问题，搜集数据，形成解释，获得答案并进行交流、检验的学习过程.

在讲完求差比较法证不等式后可做如下练习.

例5 已知a,b∈R，求证a2+b2+1≥ab+a+b.

大部分同学都是用求差比较法证明的.

让学生探究有无其他证法？

有学生在用求差比较法时用不同的配方方法.

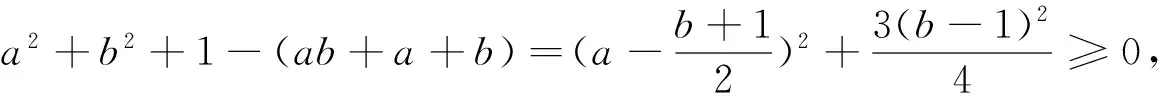
有学生用均值不等式证明.

法三：由均值不等式得a2+1≥2a,b2+1≥2b,a2+b2≥2ab,三式相加得a2+b2+1≥ab+a+b.

有学生从函数的角度考虑得到如下证法.

法四：令f(a)=a2-(b+1)a+b2-b+1,由于Δ=(b+1)2-4(b2-b+1)=-3(b-1)2≤0,故f(a)≥0，即a2+b2+1≥ab+a+b.

课堂的引导与思考激发了学生浓厚的探究欲望和兴趣，课后学生再相互交流与联想还得到了一种证法.

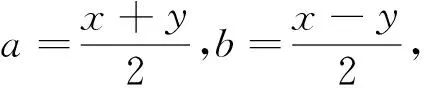
5.注重系统与渗透

(1)倡导结构教学

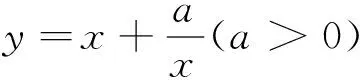
(2)立足全面渗透

“八方联系,浑然一体;漫江碧透,鱼翔浅底”,是已故著名数学特级教师孙维刚先生教学观的生动描述. 孙维刚先生认为,数学教学要站在系统的高度,每个数学概念、定理、公式等知识的教学,都要在见树木更见森林,见森林才见树木的联系状态下进行.在不等式的教学中要把不等式的知识与方法渗透在每一个章节中，贯穿于数学教学的全过程.必修1的第一章集合、第二章函数、第三章函数应用可渗透不等式的解法，必修2的直线与圆可在最值问题中渗透不等式的解法，必修3的第三章概率可结合不等式设计问题，必修4 的三角函数与三角恒等变换及平面向量中可自然结合不等式的解法与证明，必修5的数列与解三角形也自然的可与不等式联系在一起，……，总之，不等式可以说是无孔不入、无处不在.

总之，数学核心素养的培养要结合于每一个教学活动中，融合于教学的每一块具体内容当中.