教学实录与点评：直线的点斜式方程*

江苏省睢宁高级中学北校 (221200) 杜四趁 武瑞雪

《普通高中数学课程标准(实验)》[1]给出本节课的教学目标：掌握直线方程的点斜式、斜截式的特点与适用范围；能正确运用直线的点斜式、斜截式方程；感受“形”和“数”的对立和统一．教学重点：掌握直线的点斜式、斜截式方程及运用.教学难点：对直线的方程与方程的直线的对应关系的理解.

我校一位教师参加县级优质课比赛，课题名为《直线的点斜式方程》，获得较好名次.笔者有幸做为评委，现点评如下，以期与同行探讨“新授课”的有效教学模式.所用教材为现行苏教版.教学方法与手段主要为：导学案、先学后教、多学少教、问题引导、合作探究、当堂检测.

1.教学实录与点评

1.1 问题情境

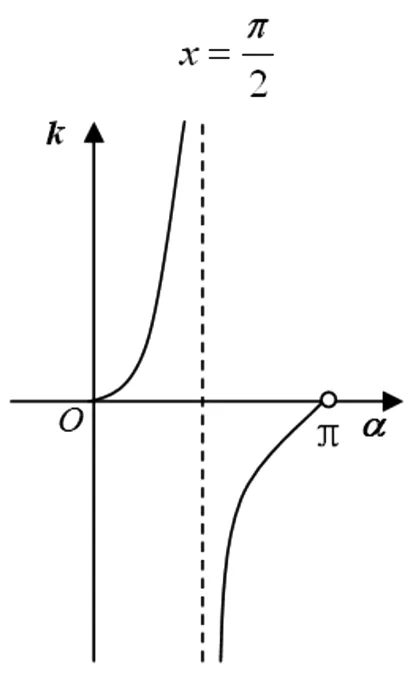
图1

问题1 斜率k与倾斜角α有什么关系？你能画出直线的斜率k与倾斜角α的关系图吗？

直线的斜率k与倾斜角α的关系图如图1所示：

问题2 若直线l经过两点P(x1，y1)，Q(x2，y2)，且x1≠x2，则直线PQ的斜率k=？

点评：通过问题1与问题2，巩固了上节所学知识，避免了遗忘，也为学生学习新知作准备，同时，还渗透了数形结合思想.

问题3 过点A(-1，3)的直线有多少条？斜率为-2的直线有多少条？过点A(-1，3)，且斜率为-2的直线有多少条？过点A(-1，3)与B(2，5)的直线有多少条？确定一条直线需要几个独立条件？

生3：无数条；无数条；一条；一条；两个.

点评：以学生熟悉的数学问题为背景，引导学生主动参与探索，通过师生共同对问题的分析和解决，使学生理解在直角坐标系中确定一条直线的独立条件有两个，即“一点一斜率”或者“两点”.

1.2 学生探究

探究1 如图2，若直线l经过点A(-1，3)，斜率为-2，点P是直线l上异于点A的任意一点，则点P的坐标(x，y)应满足什么样条件?

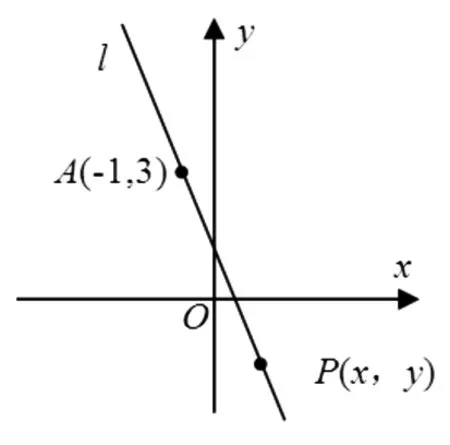
图2

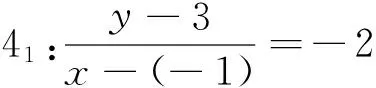
即y-3=-2[x-

(-1)]②

即2x+y-1=0③

师：点A(-1，3)的坐标满足上述各方程吗？

生5：点A(-1，3)的坐标满足方程②、③，但不满足方程①.

师：方程①出现“一个点”的残缺！

探究2 在上述问题中，直线l上任意一点的坐标都满足方程y-3=-2[x-(-1)]吗？以方程

y-3=-2[x-(-1)]的解为坐标的点都在直线l上吗？

生6：直线l上任意一点的坐标都满足方程y-3=-2[x-(-1)].反过来，以方程y-3=-2[x-(-1)]的解为坐标的点都在直线l上．

2x+y-1=0叫做直线l的方程，而直线l叫做方程2x+y-1=0的直线.

点评：(1)让学生自主地由直线的斜率公式，引出“直线的方程”概念，也为后面研究直线方程的点斜式做准备.

(2)通过具体实例，较易地突破了本节课的难点：对直线的方程与方程的直线的对应关系的理解.

探究3 若直线l经过点P1(x1，y1)，斜率为k，点P(x，y)是直线l上任意一点，那么点P的坐标(x，y)应满足哪些条件?

生7：点P的坐标(x，y)应满足y-y1=k(x-x1).

生7：不能，丢掉了点P1.

点评：由探究1到探究2，是由特殊到一般，将思考的方法、推理的过程进行类比迁移，并由此引入直线的点斜式方程.

1.3 数学理论

1.3.1 点斜式

一般地，若直线l经过点P1(x1，y1)，斜率为k，则直线l的方程为y-y1=k(x-x1)，此方程叫做直线的点斜式方程，简称点斜式．

点评：“点”和“斜”是两个独立条件的浓缩概括，是一个极为传神精准的命名，由此，让学生明白方程y-y1=k(x-x1)称为“点斜式”，是“顾名思义”.

探究4 写出下列各直线的方程.能用点斜式方程表示吗？

(1)直线l经过点P1(x1，y1)，且与x轴垂直；

(2)y轴所在的直线；

(3)直线l经过点P1(x1，y1)，且与y轴垂直；

(4)x轴所在的直线.

生8：(1)此直线斜率不存在，其方程不能表示为点斜式，方程为x=x1；

(2)y轴所在的直线斜率不存在，其方程不能表示为点斜式，其方程为x=0；

(3)此直线斜率为0，其方程能表示为点斜式

y-y1=0(x-x1)，即y=y1；

(4)x轴所在的直线斜率为0，其方程能表示为点斜式y-0=0(x-0)，即y=0.

师：用PPT展示此例中4道题目对应的图形.

点评：(1)此例中4道问题涉及的都是特殊直线，加深了学生对直线的点斜式方程的理解，了解到斜率不存在(即与x轴垂直)的直线不能用点斜式方程表示.(2)通过图形，让学生有个直观的感受，利于学生理解.

探究5 已知直线l的斜率为k，与y轴的交点是P(0，b)，求直线l的方程.

生9：由直线的点斜式方程，得所求直线的方程为y-b=k(x-0)，即y=kx+b.

点评：通过探究5，自然地引入直线的斜截式方程，让学生体会到知识的建构是水到渠成、合情合理的.

1.3.2 斜截式

方程y=kx+b由直线l的斜率k和它在y轴上的截距b确定，叫做直线方程的斜截式方程．

点评：“斜”和“截”又是两个独立条件的浓缩概括，又一个极为传神精准的命名.由此，让学生明白方程y=kx+b称为“斜截式”，也是“顾名思义”.

探究6 斜截式方程y=kx+b中的斜率k与截距b的取值范围分别是什么？

生10：R，R.

点评：(1)让学生了解到截距不同于距离，截距的本质是直线与y轴交点的纵坐标，所以它可正、可负、可零，它不同于“距离”这一概念，距离是恒为非负的，所以有“截距非距”之说．

(2)遗憾的是没有适时地将斜截式方程y=kx+b与初中所学一次函数解析式进行比较！

探究7 直线的斜截式方程与直线的点斜式方程有什么关系？两种形式的方程适用的范围？

生11：直线的斜截式方程是直线的点斜式方程的一种特殊情况.

两种形式的方程适用范围：直线的斜率存在.

点评：让学生谈对两种直线方程的认识，让学生体验特殊与一般，个性与共性的辩证关系.

1.4 数学应用

1.4.1 例题

例求下列各直线的方程：

(1)直线经过点P(-2，3)，且斜率为2；

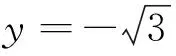
(生12、生13在黑板上板演)

点评：(1)教师表扬了做对的学生，让其享受到成功的喜悦；对做错的学生，进行了鼓励，并引导该生对其错因进行剖析，让该生不但知错，而且知其所以错．

(2)教师对求直线方程的结果进行了规范化要求，这是非常必要的：一般写成右边为0，左边按先x项，再y项，最后是常数项的顺序，且x项的系数为正，各项不含分母.

1.4.2 练习

练习1 根据下列条件，分别写出直线的方程：

(1)经过点(4，-2)，倾斜角为30°；(2)斜率为2，与x轴的交点的横坐标为-1.

点评：在生14、生15板演后，先让所有学生进行及时的反思，然后对照多媒体展示的正确解题过程进行自行订正，教师没有直接告知学生解法、答案，只是进行适当的点拔，而点拨之后，教师直接告知学生：第(2)题中直线与x轴交点的横坐标可称之“横截距”，相应地，直线与y轴交点的纵坐标称为“纵截距”，这时的直接告知应是允许的恰当的.

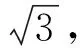
师：有不同意见吗？

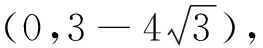
师：很好！此题第1、2两空答案唯一，但第3空答案不唯一，属于开放题.

点评：此题第3空利于培养学生的发散性思维.

练习3 在同一直角坐标系中作出直线y=2，y=x+2，y=-x+2，y=3x+2，y=-3x+2，…，这些方程表示的直线有什么共同特点？你能用一个方程表示出它们来吗？这组直线包括所有过点(0，2)的直线吗？

生19：这些方程表示的直线都过点(0，2)，能用一个方程y=kx+2表示，这组直线不包括过点(0，2)的直线x=0.

练习4 在同一直角坐标系中作出直线y=2x，y=2x+1，y=2x-1，y=2x+4，y=2x-4，…，这些方程表示的直线有什么共同特点？你能用一个方程表示出它们来吗？

生20：这些方程表示的直线是一组平行直线，它们的斜率相等，纵截距不等，能用一个方程y=2x+b表示.

1.5 当堂检测

(1)根据下列条件，分别写出直线的方程：

①经过点(4，-2)，斜率为3； ②斜率为-2，在y轴上的截距为-2.

(2)已知k∈R，则直线y=kx+5恒过点 ；直线y=k(x+5)恒过点 ；直线y=k(x-4)+2恒过点 .

(3)直线y=k(x+1)(k>0)的图像可能是( ).

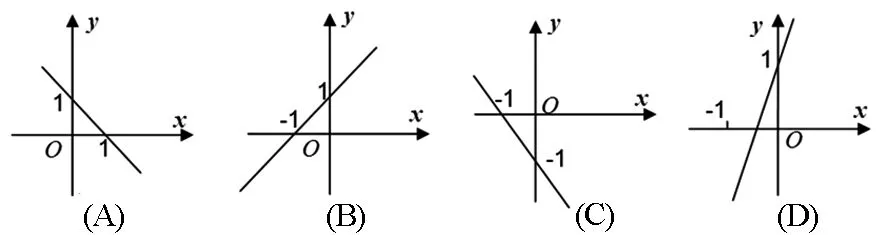
点评：练习的设置有梯度，有层次感，适合不同层次的学生学习，真正体现了新课程理念：以学生的发展为中心；让不同的学生在数学学习上得到不同的发展，实现了数学教学为所有学生服务，不同的人学不同的数学，人人学有用的数学．

1.6 回顾小结

(放手让学生小结)

点评：学生小结，教师补充，体现“学生为主体，教师为主导”的教学理念.

1.7 布置作业(反馈练习)

必做题：课本第82-83习题2.1 第1题(1)、(2)、(3)，第2题.

选做题：课本第83习题2.1 第7、8、9题.

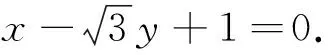
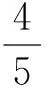
3.过点A(1，-2)、B(2，3)的直线的点斜式方程为 ，化为斜截式方程为 .

点评：分层布置作业，让不同程度的学生都有所获.另外，补充的第3题，让学生认识到直线的斜截式方程可由点斜式方程转化得到，且点斜式不唯一，斜截式唯一，同时为下节课作准备

2 总点评

2.1 优点

(1)教师的语言铿锵有力、富有激情，课堂气氛活跃.

(2)教师从容不迫地分析讲解，并给学生必要的思考、探究时间.

(3)学生在课前，在“导学案”引导下进行了预习，体现了“先学后教，以学定教”的教学理念，这让学生在课堂听讲更有目的性，对于课前有疑惑之处听得更加专注.

(4)能合理地利用问题引导、合作探究的教学手段和方法，构建知识，渗透思想、方法.

2.2 不足

(1)讲完斜截式方程之后，没有及时让学生了解直线的斜截式方程与初中所学的一次函数的区别与联系.事实上，直线的斜截式方程y=kx+b不完全等同于一次函数的解析式，因为一次函数的解析式是y=kx+b(k≠0)，而直线的斜截式方程y=kx+b中的k∈R，即{一次函数y=kx+b的图像}{斜截式方程y=kx+b表示的直线}.如课堂上能适时进行比较，则可深化学生对斜截式方程的理解，渗透“函数与方程思想”.

(2)对于“当堂检测”中学生出现的错误没有让学生先独立思考、纠错，而是由教师直接点拨、指正，这种处理方式是不恰当的.应该像处理学生在例题和练习中出现的错误一样，要放手让学生先自行纠错，而不是直接告知，因为教师的直接告知会造成学生对自己的错因剖析不透，可能下次再遇类似题目时，还会老错误重犯，导致“当时听懂，过后仍不会做题”的现象发生.(后来该教师告诉我们说，课前设计的时候，准备给学生时间自行订正的，后因时间紧迫，所以自己越俎代庖了，深感遗憾！)

[1]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京：人民教育出版社，2003，4：1.