内嵌凹槽对金属亚波长狭缝透射特性的影响

陈秀武

(兰州文理学院 传媒工程学院,甘肃 兰州 730000)

近年来，传统电磁衍射理论对周期性孔径和狭缝阵列金属薄膜结构具有远场透射增强特性效应[1]，然而无法解释的异常现象(Ebbesen效应)引起了研究者的广泛关注[2-4].包括各种亚波长金属结构的物理机理[5-10].最近，理论和实验研究表明，透射增强的主要原因有两方面：① 狭缝两端及金属表面入射光激发的表面等离子体激元(SPPs)[2]；② SPPs在狭缝中形成的类法布里-珀罗(F-P)共振[11-16].简而言之，二维孔径阵列透过增强是由表面等离子体模式谐振效应造成的，光照射在金属膜面产生的衰逝波经过端面近场增强效应的有效放大，沿着孔径传入出射端，经过放大，形成远场增强透过现象.

为了改善亚波长金属狭缝的透射特性，人们设计了不同类型的狭缝.例如锥形狭缝[17]、在狭缝入射和出射端面上加入凹槽[18]或者在狭缝内加入金属[19]等.其中，在金属狭缝内嵌入凹槽的方法具有结构简单、尺寸小、便于集成等优点，是一种调节系统的透射及反射特性的有效方法[23].基于内嵌凹槽亚波长金属狭缝可在微纳尺度上实现多路分配器[20]、滤波器[21]和反射器[22]等.

在之前的关于内嵌凹槽结构的研究中，人们对内嵌凹槽结构的透射特性进行了较深入的研究，运用不同的理论模型研究了各种特定结构参数对透射特性的影响[23-24].但是，并没有全面描述内嵌矩形凹槽结构参数的变化对透射特性的影响.文中利用有限元方法，研究了特定波长852 nm下内嵌凹槽结构对透射特性的影响.

1 结构模型

文中选择的改进二维金属Ag薄膜结构如图1所示.水平方向为半无限大，薄膜的厚度为u=1 μm，在薄膜的正中间沿y方向刻有一条通透的空气狭缝，狭缝的宽度为w=100 nm.同时在狭缝中垂直于狭缝方向，刻有一条对称的矩形凹槽，凹槽的宽度为w2，深度为h.凹槽中心到狭缝入口的距离为d.边界使用完美匹配层(PML)[25]，平面波从上向下垂直入射，调整w2，h和d来研究其对透射特性的影响.

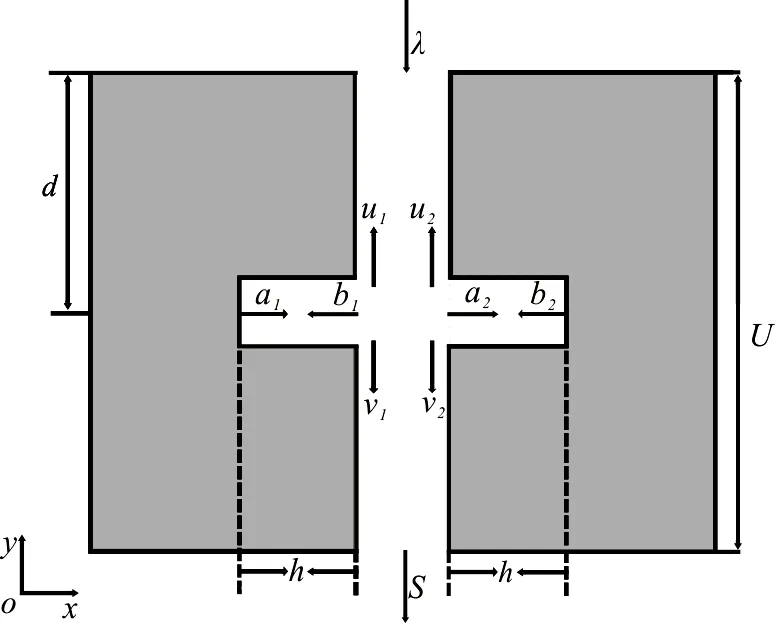
图1 亚波长内嵌凹槽纳米结构示意图

入射光源沿y方向且电场偏振方向垂直于入射方向的 TM波，波长λ=852 nm.金属Ag的介电常数ε与频率ω关系由Drude模型[26-27]给出

(1)

其中,ωp为电子等离子频率；γ为吸收系数；ω为入射光的角频率.Ag的介电常数由已知离散的介电常数拟合得出[28](εAg=-33.22+1.17i).

当TM偏振光正常入射到Ag膜上时，部分被局域在狭缝中，SPPs将在狭缝内被激发，整个狭缝可以看做SPPs的共振腔.空腔中的有效折射率neff由色散方程给出

(2)

其中，k0为入射光的波矢；β为空腔中的传播常数；εm(d)为金属和介质的介电常数.穿过狭缝的光线会在Ag膜表面发生衍射，衍射光的波矢可以表述为

(3)

当腔谐振条件满足时，出射口处的透射将增强

2k0neffL+φ=2mπ,m=1,2,3,…,

(4)

其中，m为整数；θ为SPPs在两个端口处的相位.由(4)式可知，可以通过调整狭缝宽度和膜厚调整干涉场强度,优化几何参数来改善干涉结果.

2 结果与讨论

为了定性地解释内嵌凹槽金属亚波长狭缝透射特性，研究了透射强度随w2，h和d的变化结果.归一化透射率表示为S=(T/T0)2，其中T0无凹槽时狭缝的透射强度；T为凹槽结构的透射强度，入射波波长为852 nm.

图2给出了凹槽深度h和透射率的关系，其中w2=100 nm保持不变并且凹槽位于狭缝的中心.从图2可以看出，归一化透过率S随凹槽深度h的增加出现周期性变化，周期T≈348 nm.在h为316和664 nm时，透射率显著增强.S=2.2时，比无凹槽的结构透射增强约1.5倍.h=146，494，842 nm时表现为明显的抑制效果，透射率很小.为了更好地说明这种现象的物理机制，给出了峰值处电磁场的稳态分布图，结果见图3.

图3(a-b)分别为电场在h为494和664 nm时电场的稳态分布.图3(c)为没有凹槽时的电场分布，可以看出，当h=664 nm时，有明显的透射增强.另外，无论是增强还是减弱，狭缝和凹槽内都形成了驻波模式，驻波波长在400 nm左右.在凹槽和狭缝入口和出口等有缺陷的位置，由于SPPs的激发呈现出很强的电场强度.

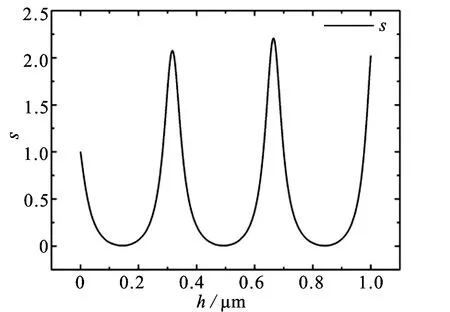
图2 归一化的透射率S随凹槽深度h变化的透射谱

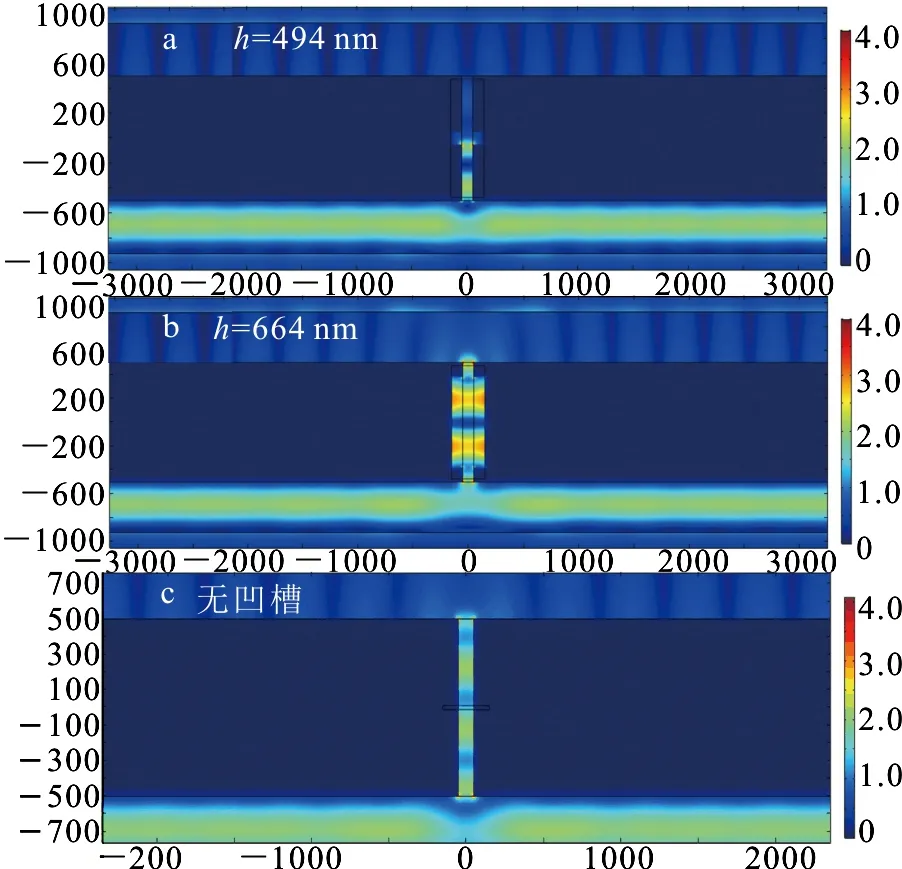
图3 稳态电场分布图

图4示给出了凹槽宽度w2变化时透射率的变化情况，其中h=100 nm保持不变，并且凹槽位于狭缝的中心d=0 nm处.从图4可以看出，当凹槽宽度改变时，归一化透过率S呈现出增强和减弱.在w2=460和758 nm时，有明显的透射增强，最大S=2.0，即与没有凹槽的结构相比，透射增强约1.4倍.h=632 nm时传输抑制明显，透射率很小.另外当w2非常小(<20 nm)时，也会出现一个透射峰.图5a-b分别为w=100 nm和758 nm时电场的稳态分布.

透射率随凹槽位置的变化如图6所示.h=100 nm保持不变，凹槽宽度w2=100 nm.从图6可以看出，归一化透过率S随着凹槽位置的变化呈现出不同程度而增强和减弱.对于对称结构，透射率同样也呈现出对称性.

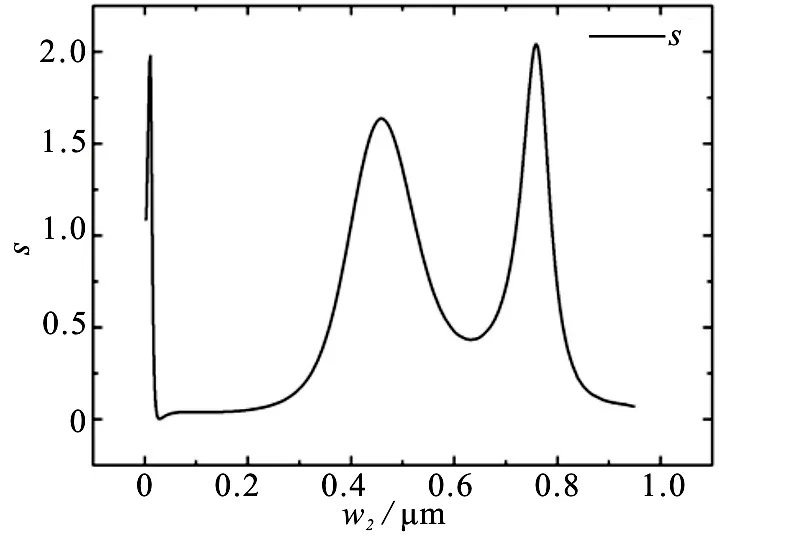
图4 归一化的透射率S随凹槽宽度变化的透射谱

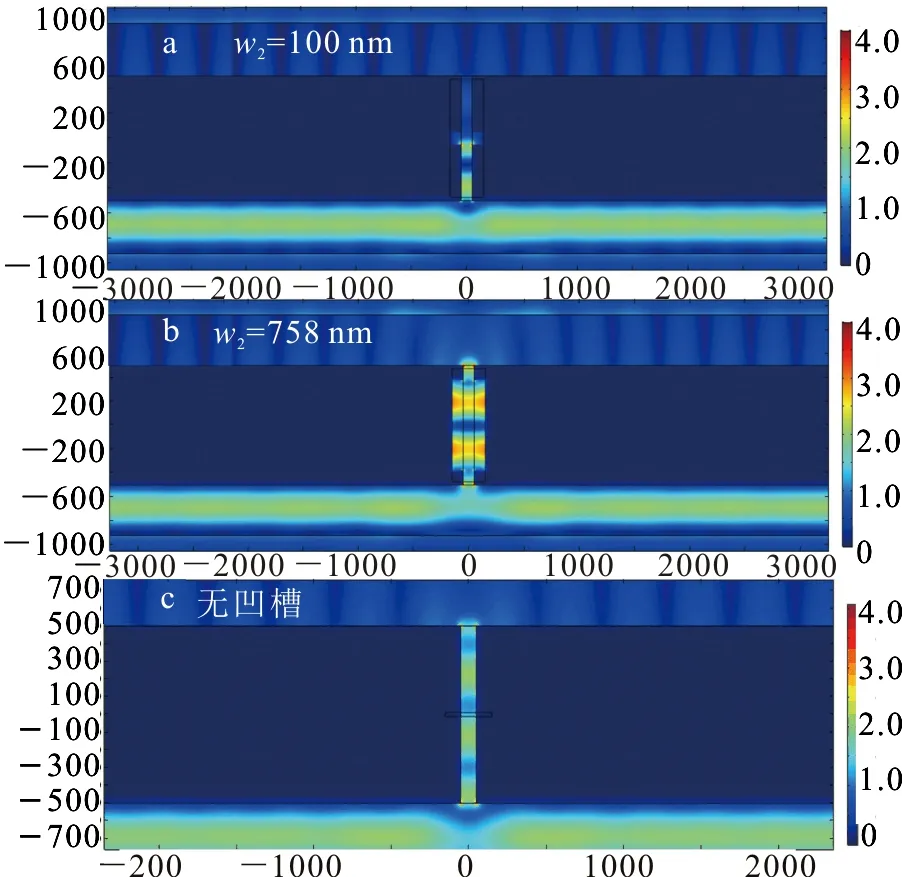
图5 稳态电场分布图

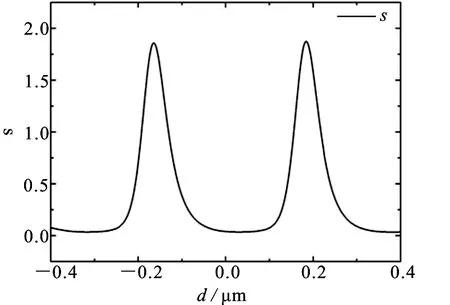
图6 归一化的透射率S随凹槽位置d变化的透射谱

图7a-b分别为d=0 nm和184 nm时电场的稳态分布. 图7c为没有凹槽时电场的分布.

对于对称结构，透射谱也呈现出对称性. 此时内嵌凹槽内的共振模式不变，凹槽位置的变化改变了SPPs的相位，从而改变了SPPs与入射波的耦合，导致不同程度的增强和减弱.

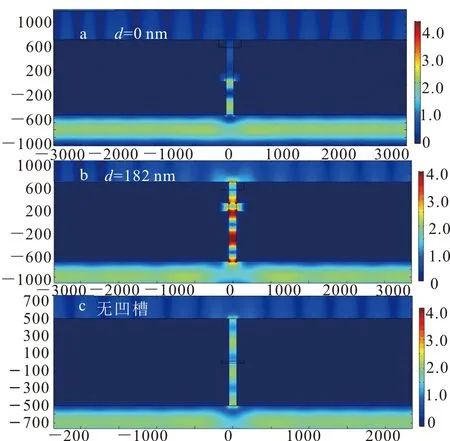
图7 稳态电场分布图

有内嵌凹槽的金属狭缝中，狭缝出口处产生了较强的电场，所以嵌入的矩形腔体结构不仅增加了金属狭缝的透射强度，而且增强了狭缝出口处的电场，包括增强表面增强拉曼散射和非线性光学效应.

缝槽和其他缺陷位置会激发出SPPs，SPPs和缝槽内的入射波进一步耦合，其结构参数的变化会影响耦合模式和传播常数，改变SPPs相位，从而出现增强和减弱.结合F-P共振效应，嵌入的矩形凹槽是另一个谐振腔.结构参数的变化同样影响了F-P共振效应.不管是增强还是减弱的结构，狭缝和凹槽等缺陷处均具有较强的电场分布.这说明有SPPs的激发，此外，狭缝的长度和宽度也会影响透射情况，当在狭缝中传播的SPPs满足一定的相位条件时，狭缝的透射率达到最大.与没有凹槽结构的狭缝相比，嵌入的矩形凹槽结构可以改变激发出的SPPs的相位和F-P腔的谐振特性，其中槽宽w2改变耦合系数，h，d改变SPPs的相位.在狭缝和凹槽的位置，SPP被激发，激发的SPP和入射波彼此耦合，并且增加了类似F-P腔的谐振效应，从而增强和衰减传输.H，w2，d和SPPs的相位因子与平面波中SPPs的耦合系数有关，引起周期性现象.

3 结论

研究了特定波长852 nm TM偏振电磁波垂直入射内嵌凹槽狭缝结构时透射特性和内嵌凹槽的形貌参数及位置的关系.研究表明，透射率随结构参数的变化表现出一定的周期性，入射波在凹槽狭缝等缺陷处会激发出SPPs，内嵌凹槽本身是一个F-P谐振腔，狭缝是另一个谐振腔.凹槽参数的变化改变了凹槽中的共振模式，从而影响到狭缝中的共振.对于对称结构，透射谱也呈现出对称性.此时，内嵌矩形的共振模式不变，凹槽位置的改变使得SPPs的相位发生变化，SPPs和入射波的耦合发生变化，从而出现不同程度的增强和削弱现象.另外，狭缝和凹槽中形成驻波模式，其波长和入射波的波长有关.

[1] EBBESEN T W,LEZEC H J,GHAEMI H F,et al.Extraordinary optical transmission through sub-wavelength hole arrays[J].Nature,1998,86(6):1114.

[2] WILLIAM L.BARNE S,ALAIN D,et al.Surface plasmon subwavelength optics.[J].Nature,2003,424(6950):824.

[3] MAIERA S A,ATWATER H A.Applied physics reviews-focused review[J].JournalofAppliedPhysics,2009,102(2):021101.

[4] EKMEL O.Plasmonics:merging photonics and electronics at nanoscale dimensions[J].Science,2006,311:189.

[5] XIE Y,ZAKHARIAN A R,MOLONEY J V,et al.Optical transmission at oblique incidence through a periodic array of sub-wavelength slits in a metallic host[J].OpticsExpress,2006,14(22):10220.

[6] LIU H,LALANNE P.Microscopic theory of the extraordinary optical transmission.[J].ChinaBasicScience,2008,452:728.

[7] YUAN G H,WANG P,ZHANG D G,et al.Extraordinary transmission through metallic grating with subwavelength slits fors-polarization illumination[J].ChinPhysLett,2007,24(6):1600.

[8] MIN C J,WANG P,JIAO X J,et al.Numerical investigation of surface plasmons associated subwavelength optical single-pass effect[J].ChinPhysLett,2007,24(10):2922.

[9] LU Y Q,CHENG X Y,MIN X,et al.Extraordinary transmission of light enhanced by exciting hybrid states of Tamm and surface plasmon polaritions in a single nano-slit[J].ActaPhysicaSinica,2016,65(20):1256.

[10] 周丽丹，栗敬钦，李平，等.高功率固体激光装置光学元件“缺陷”分布与光束近场质量的定量关系研究[J].物理学报，2011，60(2)：24202

[11] CAO Q,LALANNE P.Negative role of surface plasmons in the transmission of metallic gratings with very narrow slits[J].PhysicalReviewLetters,2002,88(5):057403.

[12] LEZEC H J,THIO T.Diffracted evanescent wave model for enhanced and suppressed optical transmission through subwavelength hole arrays[J].OpticsExpress,2004,12(16):3629.

[13] ASTILEAN S,LALANNE P,PALAMARU M.Light transmission through metallic channels much smaller than the wavelength[J].OpticsCommunications,2000,175(4):265.

[14] TAKAKURA Y.Optical resonance in a narrow slit in a thick metallic screen[J].PhysicalReviewLetters,2001,86(24):5601.

[15] HIBBINS A P,LOCKYEAR M J,SAMBLES J R.The resonant electromagnetic fields of an array of metallic slits acting as Fabry-Perot cavities[J].JournalofAppliedPhysics,2006,99(12):115.

[16] QI Y P.Characterization of extraordinary transmission for a single subwavelength slit:A Fabry-Pérot-Like formula model[J].IEEETransactionsonMicrowaveTheory&Techniques,58.12(2013):3657.

[17] RANCE H J,HAMILTON O K,SAMBLES J R,et al.Phase resonances on metal gratings of identical,equally spaced alternately tapered slits[J].AppliedPhysicsLetters,2009,95:041905.

[19] HE M D.Light transmission through metallic slit with a bar[J].SolidStateCommunications,2010,150:1283.

[20] MATSUZAKI Y,OKAMOTO T,HARAGUCHI M,et al.Characteristics of gap plasmon waveguide with stub structures[J].OpticsExpress,2008,16:16314.

[21] TAO J.A narrow-band subwavelength plasmonic waveguide filter with asymmetrical multiple-teeth-shaped structure[J].OpticsExpress,2009,17:13989.

[22] LIU J.Surface plasmon reflector based on serial stub structure[J].OpticsExpress,2009,17:20134.

[23] CHEN Z Q.Simulation of nanoscale multifunctional interferometric logic gates based on coupled metal gap waveguides[J].IEEEPhotonicsTechnologyLetters,2012,24:1366.

[24] SHEN H H,MAES B.Enhanced optical transmission through tapered metallic gratings[J].AppliedPhysicsLetters,2012,100:667.

[25] TAFLOVE A,HAGNESS S C.ComputationalElectrodynamics:TheFinite-DifferenceTime-DomainMethod[M].Boston:Artech House,2000.

[26] RAKIC A D,DJURISIC A B,ELAZAR J M,et al.Optical properties of metallic films for vertical-cavity optoelectronic devices[J].AppliedOptics,1998,37:5271.

[27] YOUNG J L,NELSON R O.A summary and systematic analysis of FDTD algorithmsforlinearly dispersive media[J].IEEEAntennas&PropagationMagazine,2001,43:61.

[28] PALIK E D.HandbookofOpticalConstantsofSolids[M].Orlando:Academic,1985.