基于移动锚节点的加权质心定位算法研究*

刘 洋，高美凤

(江南大学 物联网工程学院 轻工过程先进控制教育部重点实验室，江苏 无锡 214122)

0 引 言

在现有比较典型的基于非测距的定位算法[1]中，加权质心定位(weighted centroid localization，WCL)算法[2,3]易于实现，且计算较为简单，但缺陷是：为了达到较高的定位精度，往往需要在网络内布设大量的锚节点，造成硬件成本增加，限制了算法的应用。文献[4]提出了在加权因子中引入修正系数来提高定位精度。文献[5]根据节点间的不同距离，采用不同的权重系数，进一步提高了定位精度。文献[6]提出了对加权质心定位算法的接收信号强度指示(received signal strength indication，RSSI)距离值进行差分修正，从消除RSSI误差角度来减小累积误差。以上算法需要网络内部署较多数量的锚节点，导致了硬件成本增大。文献[7]利用少量真实锚节点的定位信息构造出虚拟静态锚节点参与定位，再结合加权质心定位算法对未知节点进行估计。文献[8]利用单个锚节点沿DOUBLE-SCAN路线飞行移动并与邻居节点进行通信，未知节点根据一定的筛选机制并结合简化的加权质心定位算法估计未知节点坐标。算法虽减少了硬件成本投入，但边界未知节点的共线问题未得到很好解决，导致节点的定位精度偏低。

针对以上问题，本文采用单个移动锚节点以既定路线遍历整个无线传感器网络的监测区域，在降低投入成本的情况下，对加权质心定位算法提出了相应的改进方案，设计了WCL-TRH(WCL-triangle RSSI hop)定位算法，并通过Matlab仿真实验对比分析了WCL-TRH,WCL,RR-WCL(WCL algorithm based on RSSI ratio)3种算法。

1 移动路径

采用单个移动锚节点，根据折线方式[9]移动路线的思想，设计了移动路径，如图1所示(“·”表示移动锚节点停留位置，即虚拟锚节点；“→”表示其移动方向和路径)。这种移动方式可以达到网络区域的尽可能覆盖，保证了网络中的未知节点可以接收到足够的移动锚节点位置信息。同时这种三角式移动广播方式，能够尽量保证网络内的未知节点处于至少3个移动位置所构成的多边形范围内部，有效地避免了边界节点共线问题，实现了更好的定位效果。

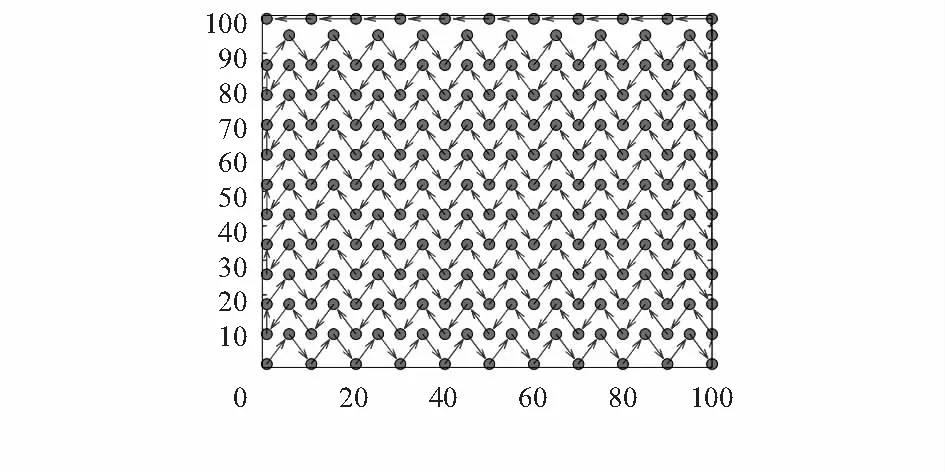
图1 移动锚节点路径规划

移动锚节点在移动过程中以时间间隔T或拐角处向未知节点广播当前位置，动态地与周围邻居未知节点建立连接关系，继续移动，直到遍历整个网络。

2 基于移动锚节点的加权质心定位算法

2.1 加权质心定位算法

加权质心定位算法的计算公式为

(1)

式中 (xi,yi)为第i个锚节点的坐标；(x,y)为未知节点M的坐标；N为未知节点的邻居锚节点个数；wi为第i个锚节点所对应的权值系数

(2)

式中di为未知节点M与第i个锚节点之间的距离，可通过式(3)无线信号传播衰减模型[10]求得

(3)

式中RSSI(d)为距离发射点d处的接收信号强度值；RSSI(d0)为距离d0处的接收信号强度值；λ为路径衰减因子，易受环境影响，一般取值范围在2～4之间；d为未知节点到锚节点间的距离，一般情况下取d0=1 m；ζo为正态随机变量，标准差为σ。

2.2 改进加权质心定位算法权重系数

为抑制环境对于RSSI值的差异影响[11]，文献[12]提出了RR-WCL算法，采用信号强度比值作为加权值，但仅采用信号强度比值作为权值，并未充分体现出不同位置处虚拟锚节点对质心位置的影响，定位效果不佳。

本文所提出的WCL-TRH算法在采用信号强度比值作为加权值的同时，根据网络中每个未知节点与邻居虚拟锚节点之间的最小跳数信息，对自身位置进行修正。若只采用最小跳数的倒数作为修正因子，虽然平均相对定位误差会降低1 %左右，但也会带来中心化效应，即定位结果不同程度地偏向于邻居虚拟锚节点位置的平均值。由于在小型网络区域，节点的最小跳数信息差别很小，所以，只采用跳数的倒数作为修正因子，降低定位误差效果不是很明显。为了扩大最小跳数对节点间实际位置的影响程度，结合指数函数y=ex，进行修正，扩大最小跳数的差异影响。

定义Rij为未知节点M分别从虚拟锚节点Bj,Bi接收到信号强度比值

(4)

根据个体差异修正后的权值系数为

(5)

式中hi为未知节点M到虚拟锚节点i的最小跳数。

由WCL-TRH算法所求得的未知节点坐标为

(6)

式中

(7)

2.3 改进的加权质心定位算法步骤

WCL-TRH算法步骤如下：

1)所有传感器节点随机分布在监测区域后，采用一个移动锚节点按照规定的路线移动。在移动的过程中，移动锚节点在每个三角形路径的拐点处停留时间T，感知周围邻近的未知节点并广播数据包Message_Loca。数据包需包含有自身移动位置坐标(xi,yi)、标号IDi、间隔跳数值Hops(始化为零)以及信息源标记(source=-1表示由移动锚节点发送的信息，source=0表示由未知节点发送的信息)

Message_Loca(IDi,(xi，yi),Hops,source)

2)未知节点根据接收的移动锚节点Message_Loca信息，首先测量获取该信息的接收功率ri，然后记录与移动位置i的间隔跳数值Hopsi=Hops+1。如果接收的信息源标记source=-1，一定是未知节点第一次接收到的信息，无需比较，只需将跳数加一并将信息源标记改为source=0，然后进行广播；如果未知节点接收到的广播信息是从其他未知节点转发，那么首先判断是否第一次接收到位置标记i的信息包，若是，则记录标号i，并将跳数进行加一处理；否则，比较曾记录的跳数值，保留较小跳数值对应的标号信息，处理后继续广播。

3)若移动锚节点在停留当前位置j时，接收到来自未知节点发送的数据包时，如果是第一次接收到标号为i的信息时，记录并处理标号为i的跳数值，同时记录位置i，j的连通关系；如果不是第一次接收到该标号信息，则与原记录值进行比较，保留较小跳数的信息。

4)移动锚节点沿既定路线移动结束后，监测区域内的未知节点根据记录的信号强度值、最小跳数及相关虚拟锚节点的位置坐标，进行定位。若接收的虚拟锚节点数至少3个，则直接利用式(6)计算未知节点的估计坐标；若接收到的虚拟锚节点数为1或2个，则利用式(8)估算未知节点坐标

(8)

式中RSSIi为未知节点接收到的移动锚节点位于位置i处所接收到的信号强度；(xi,yi)为移动锚节点处于该位置下的坐标。

3 WCL-TRH仿真与分析

利用MATLAB对算法进行仿真实验以验证改进算法WCL-TRH的性能。假设在100 m×100 m的正方形区域内，随机布设200个未知节点，节点通信半径为10 m的圆形区域。

3.1 定位精度分析

平均相对定位误差为

(9)

式中m,n分别为虚拟锚节点和节点数量，rest为未知节点的估计位置，rreal为未知节点的实际位置，R为节点的通信半径。当未知节点从50增加到300个，比较WCL，RR-WCL和WCL-TRH 3种算法的相对平均定位误差，如图2所示。

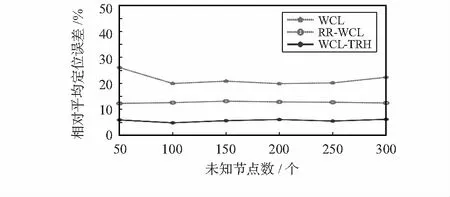
图2 相对平均定位误差

可以发现：WCL的相对平均定位误差在19.86 %～26.06 %波动；而RR-WCL和WCL-TRH的平均相对定位误差分别在12.25 %～13.11 %,4.77 %～6.11 %波动，且随未知节点数的增加，相对平均定位误差总体变化趋势较为平缓，即未知节点数量对RR-WCL和WCL-TRH算法基本无影响；WCL-TRH的定位精度较WCL算法提高了15.09 %～19.95 %，较RR-WCL算法提高了7.00 %～7.48 %。

3.2 稳定性分析

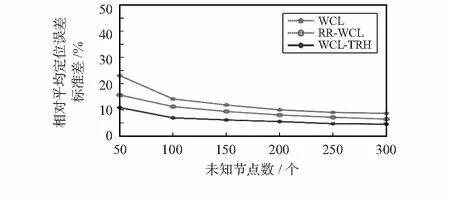
图3 节点相对平均定位误差标准差

可以看出：WCL，RR-WCL和WCL-TRH算法的标准差整体随未知节点数的增大先减小后趋于稳定；WCL-TRH算法的定位误差标准差明显低于WCL算法和RR-WCL算法的定位误差标准差，说明WCL-TRH的稳定性要优于WCL算法和RR-WCL算法。

3.3 广播间距影响分析

在相同的仿真环境下，改变移动锚节点的广播间距，从图4中可以发现，节点的相对平均定位误差随广播间距增大而增大。这是由于在网络区域内，移动锚节点的广播间距代表了虚拟锚节点的数量，广播间距越小，虚拟锚节点的数量越多，定位精度越高；反之则定位精度越低。另外，通过改变移动锚节点的通信半径大小，可以发现当移动锚节点的广播间距与其通信半径相同时，网络内未知节点的相对平均定位误差最小。因此，在考虑实际应用成本以及定位精度的情况下，选择移动锚节点广播间距与其通信半径相当时定位效果最好。

图4 移动锚节点广播间距对相对平均定位误差影响

3.4 通信半径影响分析

相同的仿真环境下，改变节点的通信半径后，节点的相对平均定位误差如图5所示。

图5 通信半径对相对平均定位误差影响

可以看出：当移动锚节点广播位置不变时，随着节点的通信半径增加，节点的相对平均定位误差逐渐减小。这是由于在一定范围内，节点通信半径的增大会提高网络的连通度，使得未知节点可以接收的移动锚节点数据包数量增多，其位置也可以越来越趋近于邻居移动锚节点位置所构成的多边形中心，从而使得未知节点的相对平均定位误差有所提高。

4 结束语

在不增加硬件资源的前提下，提出了WCL-TRH算法。采用了单个移动锚节点以既定的合理路径遍历整个定位区域，采用了一种改进的加权系数计算方法对未知节点进行定位。在充分考虑了邻居虚拟锚节点位置对未知节点的影响情况下，利用未知节点的接收信号强度比值以及邻居虚拟锚节点间的最小跳数等信息对未知节点的位置进行估计。仿真实验表明：WCL-TRH算法可以得到较小的定位误差和较高的稳定性，且节约了硬件成本。接下来的工作是移动锚节点根据网络内节点的不同分布情况采用动态路径的移动方式对未知节点进行定位。

[1] 彭 宇,王 丹.无线传感器网络定位技术综述[J].电子测量与仪器学报,2011,25(5):389-399.

[2] Blumenthal J,Grossmann R,Golatowski F,et al. Weighted centroid localization in ZigBee-based sensor networks[C]∥IEEE International Symposium on Intelligent Signal Processing,Spain:IEEE Instrumentation and Measurement Society,2007:1-6.

[3] 王 宇.基于灰度质心法的雷达干扰源定位方法研究[J].自动化技术与应用，2016，35(2)：63-66.

[4] 张先超,刘兴长，张春园.基于次锚节点的无线传感器网络改进加权质心定位算法[J].传感器与微系统,2015,34(2):143-146.

[5] Zhao Jijun,Zhao Qingwei,Li Zhihua,et al.An improved weighted centroid localization algorithm based on difference of estimated distances for wireless sensor networks[J].Telecommunication System,2013,5(1):25-31.

[6] 花 超,吉小军，蔡 萍，等.基于RSSI差分修正的加权质心定位算法[J].传感器与微系统,2012,31(5):139-141.

[7] 于海存,石为人,冉启可，等.基于虚拟静态锚节点的加权质心定位算法[J].传感技术学报,2013,26(9):1276-1283.

[8] 鲍金凤,游晓鹏.WSNs中移动信标辅助的加权质心定位算法[J].计算机技术与发展,2013,23(10):27-30.

[9] 李瑞雪,房至一,仪婷婷.基于可规律性移动锚节点和接收信号强度指示器的改进DV-Hop定位算法及其性能分析[J].吉林大学学报:工学版,2011,41(2):435-441.

[10] Alippi C,Vanini G.Wirsless sensor networks and radio localization:A metrological analysis of the MICA2 received signal strength indicator[C]∥Proceedings of the 29th Annual IEEE International Conference on Local Computer Networks,USA:IEEE Computer Society,2004:572-582.

[11] Rabaey J M,Ammer M J,Silva J L D,et al.Picorodio supports Ad Hoc ultra-low power wireless networking[J].Computer,2000,33(7):42-48.

[12] 杨新宇,孔庆茹,戴湘军.一种改进的加权质心定位算法[J].西安交通大学学报,2010,44(8):1-4.

[13] Rezazadeh J,Moradi M,Ismail A S,et al.Impact of static trajectories on localization in wireless sensor networks[J].Wireless Networks,2015(3):809-827.