基于FPGA的多通道心电信号实时滤波与压缩*

张光普，陈日清，付轶帆，吴 剑

(清华大学 深圳研究生院 深圳市无损监测与微创医学技术重点实验室，广东 深圳 518055)

0 引 言

心电(electrocardiography,ECG)信号是微弱的电生理信号，易受人体自身、外界环境及测量仪器的影响，产生如工频噪声、基线漂移、极化电压和肌电干扰等类型的干扰[1]。此外多通道(32导联及以上)心内ECG采集时单通道的采样率可达2 kHz，增加了数据传输和存储的难度。目前，ECG去噪有自适应滤波、有限长单位冲激响应(finite impulse response,FIR)滤波、模糊逻辑、经验模式分解和小波变换等方法[2]。其中离散小波变换(discret wavelet transform,DWT)因不需先验知识，能根据信号自身选取阈值的特性，近年来被广泛应用于ECG滤波中[3,4]。本文采用基于FIR低通与DWT相结合的方法，前者在滤波的同时缩短了信号的带宽，有利于DWT对频带进行更为精细的分解和滤波。ECG信号有直接压缩、变换域压缩和特征参数提取压缩等3种方法[5]。其中变换域压缩可以去除信号相关性并减小冗余，因而备受关注，有Karhunen-Loeve变换(KLT)，傅立叶变换(Fourier transform,FT)，余弦变换(cosine transform,CT)和小波变换(wavelet transform,WT)[6～10]等。其中小波变换具有良好的时频定位和能量集中特性，本文采用基于DWT的SPIHT算法对ECG信号进行压缩。SPIHT算法在图像压缩领域取得了巨大的成功[11]，经改造后对ECG的压缩也取得了良好的效果[12]，算法原理包括：用子集划分搜索算法对小波系数按幅值进行部分排列，利用小波系数层间的相关性假设和顺序输出系数的比特位[13]。

针对ECG去噪和压缩存在算法复杂、处理数据量大和计算时间长的问题，提出了一种基于现场可编程门阵列(field programmable gate array,FPGA)的方法来实现多通道ECG信号的实时滤波和压缩。

1 方 法

基于FPGA对ECG进行滤波和压缩的实现方法如图1所示，采用8个8-1多路开关配合8输入ADC完成64路ECG的分时采集，减少多通道采集对ADC芯片和FPGA管脚的用量。信号x(n)进入FPGA后，经1-64分解器分时传入64通道的FIR低通滤波、Coif1小波分解和阈值处理模块，完成64路信号的并行滤波。滤波系数由64-8多路开关并行送入8个SPIHT数据压缩模块进行压缩。压缩后由8-1多路开关经通用串行总线(universal serial bus,USB)传输模块送入上位机。

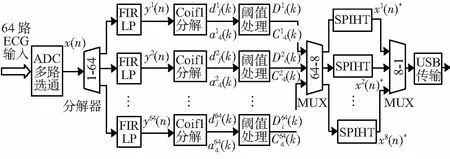
图1 实现方法框图

1.1 FPGA中的FIR低通滤波实现

设计采用31阶等波纹FIR低通滤波器去除100 Hz以上噪声，N阶FIR滤波实现的卷积公式为

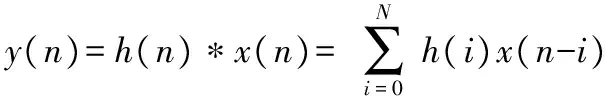
(1)

式中h(n)为滤波器系数；x(n)为输入信号；y(n)为输出信号；N为滤波器阶数。FIR滤波器在FPGA内由分布式算法(distributed algorithm,DA)[14]实现，利用查找表(look-up table,LUT)映射乘积项，代替通用乘法器的使用，广泛地应用在计算乘积和之中，是一项重要的FPGA技术。2个长度为N的向量c与x的内积

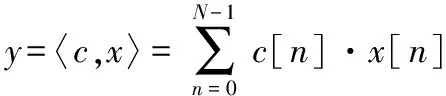
(2)

式中y为输出变量。如果系数c[n]为已知常数，x[n]为变量，则B+1位有符号DA系统的x[n]表达式

xb[n]∈[0,1]

(3)

式中xb[n]为x[n]的第b位；x[n]为x的第n次采样。结合式(2)和式(3)可得

(4)

即2N字宽、预先设定程序LUT接收N位输入向量xb=[xb[0],xb[1],…,xb[N-1]]后输出f(c[n],xB[n])或f(c[n],xb[n])。每个输出均由相应的二次幂加权并累加，在N次查询循环后即完成了内积y的计算[14]。由于滤波器系数h(n)为偶对称常数，并可用压栈来实现x(n-i)中的移位i，因此，卷积可由内积实现。Arria V FPGA采用8输入的LUT，因而31阶的滤波器仅需4个LUT即可，FIR低通滤波实现如图2。

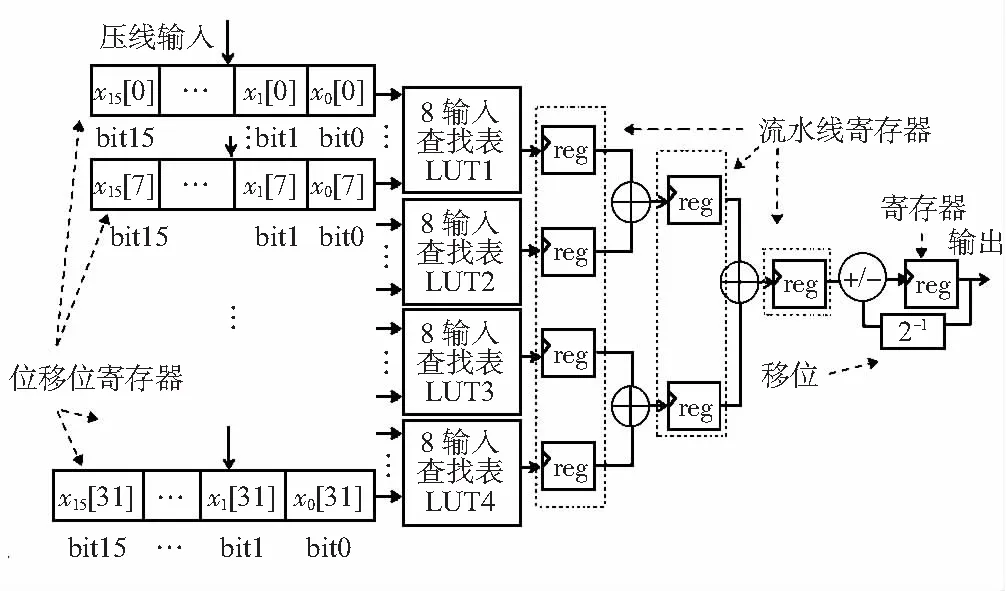
图2 FIR低通滤波在FPGA中的实现方法

1.2 FPGA中小波滤波实现方法

设计中，Coif小波基的分析滤波器由Mallat多分辨率实现[15]，既可以有效去除ECG噪声又有助于实现数据压缩[16]。分解的层数影响了滤波精度和压缩性能，设计采用4层Coif1小波分解，并选取各尺度下相应的阈值完成软阈值去噪，以期获得更好地滤波效果。方法实现分为2个部分：分解缓存和系数处理。分解缓存部分使用多相双信道滤波器组[14]来实现小波分解，其中多相滤波器由简化加法器图(reduced adder graph,RAG)实现，不但提高了运行速度同时减少了乘法器使用。Coif1小波的高频分析滤波器H(z)和低频分析滤波器G(z)的多相实现如式(5)

(5)

式中H0(z2),H1(z2),G0(z2)和G1(z2)为分解后的多相滤波器。低通滤波后，信号经过H(z)输出的第j层细节系数和G(z)输出的第四层概貌系数缓存至随机存取存储器(random access memory,RAM)中，j=1,2,3,4。当缓存达到预设值时，依次从第一至第四层RAM中读出32个小波系数，d1(k),k=0,1,…,15;d2(k),k=0,1,…,7;d3(k),k=0,1,2,3;d4(k)和a4(k),k=0,1，如图3。

图3 分解缓存在FPGA中的实现方法

读出的系数依次传入系数处理部分完成去噪，软阈值去噪如式(6)，当|ω|<λ时，令其为0；否则，令其减去阈值，即

(6)

式中ω与ωλ分别为处理前、后的小波系数；λ为该尺度下的阈值。

在实现时，小波系数分2路输入，一路作为待处理系数直接进入去噪环节，另一路则依次经过取绝对值、排序和求阈值环节来求取各层的阈值。其中，取绝对值环节将系数由补码转化为无符号源码。排序环节通过对绝对值|dj(k)|排序获取各层中位数，32个系数输入后，每层中相邻两个系数构成一个偶或奇数比较对，根据比较对的比较结果使能系数间的交换，根据总比较结果决定是否完成三层|dj(k)|的排序。流程如下：

1)对于第j层的系数，j=1∶3有

a.若|dj(2k+1)|>|dj(2k) |，则|dj(2k+1)|↔|dj(2k)|，k=0～24-j-1。即交换相邻系数；否则,不变。

b.若|dj(2k)|>|dj(2k-1) |，则|dj(2k)|↔|dj(2k-1)|，k=1～24-j-1；否则,不变。

2)如果|dj(0)|≤…≤|dj(25-j-1) |，j=1～3，则排序完成；否则，回到步骤(1)进行下一循环。如，当|d3(0)|～|d3(3)|为3,1,5和6时，本层的排序流程如图4，每轮对箭头所指的奇或偶数比较对比较交换，经过5轮后即可完成由小到大排序。

图4 第三层排序示意

每层的中位数进入求阈值环节后，通过移位加实现与噪声强度估计值的乘积，求取各尺度下的阈值。去噪环节利用各尺度下阈值，按照式(6)对系数进行处理，实现软阈值的施加。处理后的高频系数dj(k)由Di(k)表示,低频系数a4(k)用C4(k)表示，其中，i=1,2,3,4。

1.3 SPIHT压缩

设计利用FPGA的并行处理和可编程特性，对文献[13]中的算法进行了改造，大幅降低了原算法的复杂度并缩短了比较迭代等过程所用时间，提高了处理的实时性。

1.3.1 SPIHT数据压缩实现

处理后的小波系数从第一层D1(k)(k=0,1…15)至第四层D4(k),C4(k)(k=0,1)依次进入数据压缩模块。为满足层间相关性假设，系数先通过由RAM和地址计数器构成的排序环节将输入顺序变为C4(k)至D1(k)。为便于编码，转源码环节将排序后的系数从补码转化为源码。之后的取阈值环节则将源码中模最大值的最高二进制数筛选出来，作为初始阈值和源码系数一起传入编码环节。编码环节由寄存器、选通开关、计数器、比较器和逻辑门等组成，构成SPIHT算法的实现主体，如图5，图中的黑圆点表示两个子代总比较结果的逻辑或。

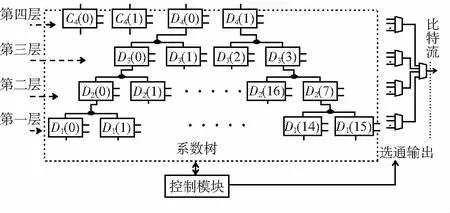
图5 编码环节结构

图5中系数树共有4层，每个方框代表一个以系数命名的系数单元。选通输出部分由两级多路开关组成，用于选通输出各系数单元的总比较结果、自身比较结果、自身符号位和子代比较结果。系数单元结构如图6，系数模块存储小波系数；阈值模块存储阈值；比较模块存储两者的比较结果，大于阈值时自身比较结果为1，称系数有意义；否则，为0，无意义。符号模块是系数符号位已输出标志，1表示已输出，0未输出；若系数为正，自身符号位为0；否则，为1。总比较结果是子代和自身比较结果的逻辑或，为1时表示自身与其两个子代中有大于阈值的系数；0,则没有。子代比较结果是其两个子代总比较结果的逻辑或。

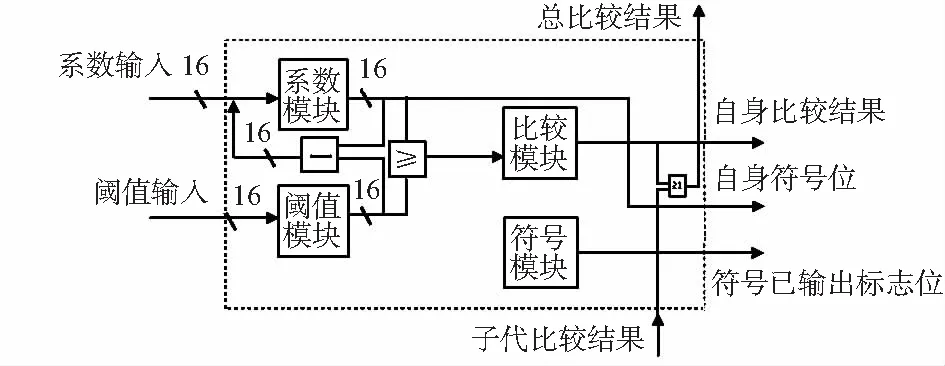
图6 系数单元结构

编码环节的SPIHT算法实现流程为：

1)将初始阈值T和小波系数C4(k)至D1(k)存入系数树中对应的系数单元，并将比较结果锁存至各自的比较模块，同时存储T到loop_cnt寄存器中作循环控制，之后执行步骤(2)。

2)判断loop_cnt是否为零，如果为零，则发出信号all_zero=1，表示输入系数全为零，执行步骤(6)；否则，转到步骤(3)。

3)系数比较输出。系数的比较输出流程伪代码如下，不同系数的流程有所区别。从第四层至第一层，由左向右依次对系数单元判断输出。

a.if(Di(k)T==1){

y=1;

b.if(Di(k)>=T){

y=1;Di(k)=Di(k)-T;

if(Di(k)S==0){

y=Di(k)Sgn;

Di(k)S=1;

}

c.y=Di(k)B;

d. }elsey=0;

e.}elsey=0;

其中，第i层k个系数用Di(k)表示；Di(k)T代表该系数的总比较结果；Di(k)S代表符号位已输出标志；Di(k)Sgn代表自身符号位；Di(k)B代表子代比较结果；T为阈值；y代表输出比特。

①对系数D4(k)，k=0,1和D1(k)，k=0～15,比较输出包括了上述步骤(b)和步骤(d)。

②对系数D4(k)，k=0,1和D3(k)，k=0～3，包括步骤(a)、步骤(b)、步骤(d)和步骤(e)。

③对系数D2(k)，k=0～7，包括步骤(a)～步骤(e)。

对Di(2k+1),k=0～24-i-1,i=1～4在比较输出后还有判断转移环节，如表1，表中第一行的数字代表判断的顺序，第一列为有此环节的系数。每个数字有2列，第一列为判断条件，第二列为当判断条件为真(1)时下个比较输出的系数，若为假(0)则检查下个判断条件，以此类推，若一行的判断条件均为假，则执行步骤④。例如对D4(1)，若D4(0)T为1则转移至系数D3(0)；若为0则检查D4(1)T，若为1则转移至D3(2)；否则，转到步骤④。

④loop_cnt右移一位，并判断是否为零。若为0则执行步骤⑥;否则,转到步骤⑤。

⑤将每个系数单元中的阈值右移一位，并锁存新的比较结果，回到步骤③。

⑥编码环节结束。

编码环节输出的位流经缓存整合为32 bits，与初始阈值一起由USB模块送入上位机。上位机则根据初始阈值和编码数据进行解压缩与信号重建。

表1 系数的判断转移环节

2 实验结果

设计使用MIT-BIH T-wave Alternans Challenge和Motion Artifact Contaminated ECG[17]的数据来验证提出的方法，选取的ECG数据采样率为500 Hz，采样精度为16 bits。FIR低通滤波器系数由MATLAB的Filter Design Analysis工具生成，采样率500 Hz，通带截止频率100 Hz的31阶等波纹滤波器。图7为加入白噪声的twa03m样本滤波前后的对比，图7(a)为加入白噪声的信号，图7(b)为软件滤波重建的信号，图7(c)为设计中硬件滤波重建后的信号。

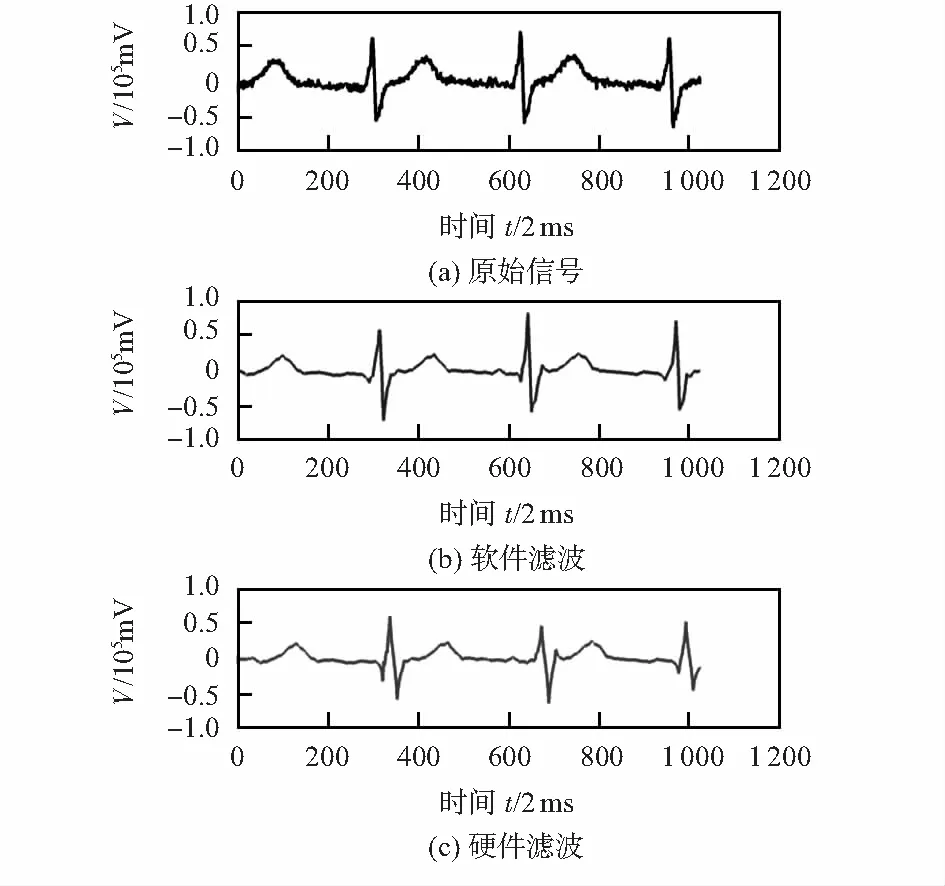
图7 twa03m的噪声信号和重建信号

表2为twa03m样本加入不同强度白噪声后滤波前后的信噪比(signal to noise ratio,SNR)。由图7和表2可知，本文方法对白噪声具有较强的抑制能力，在较强噪声环境下仍能恢复信号的整体形态并保留重要特征；相较于软件滤波，FPGA滤波的效果同样显著，两者去噪能力相当。滤波后SNR平均提高了6.4 dB最高达7.4 dB，达到了有效抑制噪声的目的。

表2 滤波前后信噪比 dB

表3为通道9的twa03m信号滤波后，分10段压缩的压缩比和压缩时间，其中，1为原始信号，2为幅值加倍后结果，每段压缩32个16 bits系数，输出为bit，压缩时间以FPGA的时钟周期数来衡量，设计使用50 MHz时钟。表4为10个不同通道的twa03m信号压缩比与压缩时间，每个通道输入320个16 bits系数，输出为bit。

表3 压缩比及压缩时间(f=50 MHz)

从表3和表4可知，压缩时间随着压缩比的降低而增加；压缩比及压缩时间和输入信号幅值有关，随着幅值增加压缩比有所降低，因为需要更多的比特位来表征信号；压缩时间也会相应增加，由于要进行更多轮的系数比较输出，但增加的时间有限，仍然能满足实时压缩的需求。信号的局部压缩比起伏较大，整体压缩比较高且稳定。

3 分析与讨论

ECG信号经过2次数字滤波，各频段噪声得到了有效地抑制，SNR有了较大提升；得益于流水线寄存器的使用，滤波可在100个时钟周期内完成，相对于采集速度完全可以实现实时滤波。由于FPGA实现时滤波器系数量化为整形，波形的光滑度有所下降，但并不影响信号的整体形态和特征参数的获取。改造后的SPIHT算法复杂度和压缩时间显著降低，并行性和实时性增强，取得了较高的压缩比，减轻了多通道ECG的传输量和存储量的负担；压缩时间通常在几百个时钟周期内，为实现多通道ECG的实时处理提供了可能。

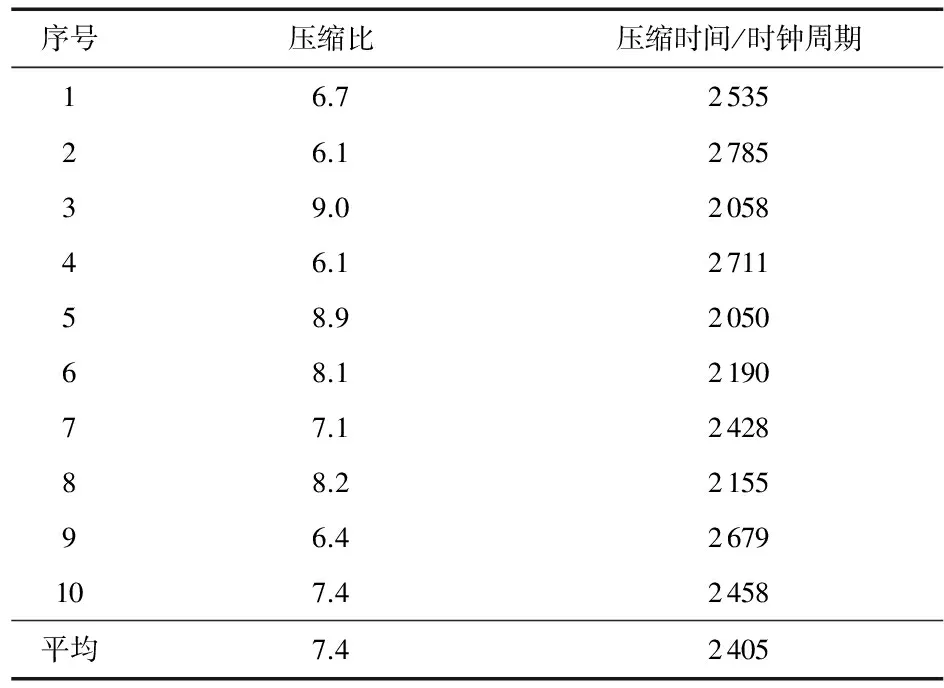
表4 twa03m的10个通道压缩比及压缩时间(f=50 MHz)

4 结 论

通过滤波有效地抑制了来自人体自身和外界环境的噪声干扰，提高了SNR；SPIHT压缩则减少了传输的数据量，保证了传输速率，提高了实时处理的能力。为进一步增强滤波与压缩性能，可以选取高阶的Coiflet小波基[18]或增加分解层数，若结合FPGA的硬核处理系统(hard-core processing system,HPS)部分，则可构成一个功能更为完善的ECG采集与处理系统。

[1] Bai Yingwen,Chu Wenyang,Chen Chienyu,et al. Adjustable 60 Hz noise reduction by a notch filter for ECG signal[C]∥International and Measurement Technology Conference,Italy:IEEE,2004:1091-5281.

[2] Sarang L Joshi,Rambabu A Vatti,Rupali V Tornekar.A survey on ECG signal denoising techniques[C]∥2013 International Confe-rence on Communication Systems and Network Technologies,Washington DC:IEEE Computer Society,2013:60-64.

[3] Chmelka L,Kozumplik J.Wavelet-based Wiener filter for electrocardiogram signal denoising[C]∥Computers in Cardiology,2005:771-774.

[4] Mithun P,Prem C Pandey,Sebastian T,et al.A wavelet-based technique for suppression of EMG noise and motion artifact in ambulatory ECG[C]∥2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society,Boston:IEEE,2011:7087-7090.

[5] Andrews C A,Davies J M,Schwarz G R. Adaptive data compression[J].Proceedings of the IEEE,1967,55(3):267-277.

[6] Ahmed S M,Al-Shrouf A,Abo-Zzahhad M.ECG data compression using optimal non-orthogonal wavelet transform[J].Medical Engineering Physics,2000,22(1):39-46.

[7] Miaou S G,Lin C L.A quality-on-demand algorithm for wavelet-based compression of electrocardiogram signals[J].IEEE Trans on Biomed Eng,2002,49(3):233-239.

[8] Al-Shrouf A,Abo-Zahhad M,Ahmed Sabah M.A novel compression algorithm for electrocardiogram signals based on the linear prediction of the wavelet coefficients[J].Digital Signal Process,2003,13(4):604-622.

[9] Ahmed S M.ECG data compression algorithm based on the combination of singular value decomposition and discrete wavelet transform[J].J Eng Sci,2005,33(6):2267-2280.

[10] Sabah M A.ECG signal compression using combined modified discrete-cosine and discrete-wavelet transforms[J].J Eng Sci,2006,34(1):215-226.

[11] Said A,Pearlman W A.A new,fast and efficient image CDEC based on set partitioning in hierarchical trees[J].IEEE Trans on Circuits and Systems for Video Technology,1996,6(3):243-250.

[12] Lu Zhitao,Pearlman W A.An efficient,low-complexity audio coder delivering multiple levels of quality for interactive applications[C]∥Proceedings of 1998 IEEE the Second Workshop on Multimedia Signal Processing,1998:529-534.

[13] Lu Zhitao,Kim Dongyoun,Pearlman W A.Wavelet compression of ECG signals by the set partitioning in hierarchical trees(SPIHT)algorithm[J].IEEE Transactions on Biomedical Engineering,2000,47(7):849-856.

[14] 贝 斯.数字信号处理的FPGA实现[M].刘 凌,胡永生,译.北京：清华大学出版社，2006:50-54.

[15] 胡广书.现代信号处理教程[M].北京：清华大学出版社，2004：246-375.

[16] Stephane Mallat.A wavelet tour of signal processing[M].3 ed.Manhattan:Academic Press,2008:191-444.

[17] PhysioNet.PhysioBank[DB/OL].(2016—10—17),http:∥www.physionet.org.

[18] Daubechies I,Lagarias J C.Tow-scale difference equations:IL.Local regularity,infinite products of matrices and fractals[J].SIAM J of Math Anal,1992,23(4):1031-1079.