超声探头外声场在测量管道上的仿真分析*

王月明，王 鹏，袁小健, 张瑶瑶

(内蒙古科技大学 信息工程学院，内蒙古 包头 014010)

0 引 言

超声法检测管道内的流体参数以无污染、非接触测量等优点，被国内外广泛关注[1]。薛明华对超声波在悬浊液中的传输进行了理论推导，求得声衰减系数、声速与介质参数的关系[2]。蔡小舒等人将近年来超声波测量混合物浓度的理论进行了总结，并通过改进反演算法从接收的声信号中求得混合物的粒径分布[3,4]。上述研究中，均以平面波入射为条件，忽略了探头本身对声场的影响，而实际测量中发现，探头外的声场具有一定分布规律，并非一个理想的平面波，在不同的接收位置，接收到的声信号不同。本文以常用的圆平面探头为研究对象，进行理论分析并利用有限元软件COMSOL管道中的声场分布进行仿真，通过改变声波频率和介质的衰减系数，观察频率和衰减系数对声场分布的影响，最终得到探头最佳的摆放位置。

1 声场分布理论

1.1 圆形平面探头外声场

当忽略流体介质的声衰减，声源发出的波为连续简谐波时，圆形平面探头声源外的声场分布如图1所示。声束分为主声束瓣和副声束瓣，超声波能量大部分集中在主声束内(区域A内)，图中右侧曲线为指向性函数曲线。

通过指向性函数可以求得指向角为θ0，半径为a的圆形活塞指向性函数如下

图1 圆形平面探头外声场分布

(1)

(2)

声源轴线上的声压分布为[5]

(3)

(4)

1.2 流体介质的声衰减

上述分析认为介质无衰减，而在实际流体介质中存在声衰减，衰减大致由粘滞损耗、热传导、散射等引起。对于衰减系数的计算，研究就不同性质的流体，考虑了不同的衰减机制，提出了很多计算衰减的理论模型，如ECAH模型、H&T模型、BLBL模型等[6～8]。ECAH模型适用于稀释的悬浊液，考虑了粘滞、热传导和散射等衰减机制，被广泛熟知和认可，其公式如下[9]

(5)

式中κ=ω/cs(ω)+jαs(ω)；kc为压缩波复波数；αs和cs分别为颗粒两相介质的声衰减系数和声速；φ为颗粒相体积浓度；3φ/4R3为单位体积中的颗粒数。通过这种表达方式可以将总的能量损失简单地设想为与单位体积内颗粒数目浓度成正比，An为压缩波散射系数[10]。

在声场中，声压随距离的增加成指数性减小，即

p=p0e-ax

(6)

因此，可以将式(4)中加入介质引起的声衰减量写为

(7)

2 仿真和分析

2.1 模型建立

为了分析探头在管道内声场分布情况，利用COMSOL建立管道的轴向几何模型，如图2所示，区域A为输送管道的内部，阴影区为完美匹配层，为声场边界的一种处理方式，当声波传到边界时，会被全部吸收而不产生反射，区域A的左侧为输送管道的入口，右侧为出口，上侧边界中间放置为超声发射探头，在A区下边界放置接收探头。

图2 管道轴向几何模型

模型选择“压力声学,频域”接口，主要的参数如表1所示。

表1 模型的主要参数

区域A材料选择为空气，探头的初始声压设置为1 Pa。设置网格尺寸为c/f/6，c为流体介质中的声速。求解器的研究类型设为稳态，采用直接线性求解器MUMPS。

2.2 仿真结果分析

2.2.1 频率对声场的影响

不同探头对应不同的声波频率，当频率不同时，管道内的声场分布不同，选取管道壁上的声压数据绘制曲线，如图3所示，可以发现：频率越大，声束聚集性越好，主声束范围越小，越靠近主轴声压值越大，从声压级,图4亦可看出:如频率为50 kHz时，两条声压级值极小值的线OA和OA′中间范围对应着主声束，主声束在管道壁上的范围AA′约为22 cm。

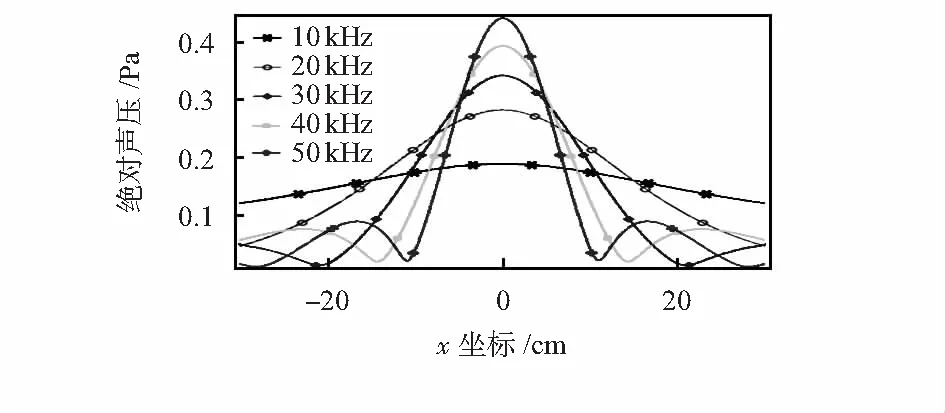
图3 管道壁上不同频率的声压分布

图4 声压级分布

2.2.2 衰减系数对声场的影响

在仿真中，确定其他条件，只改变声波的衰减系数，系数分别设为0，5，10 Np/m。仿真发现声衰减系数不同，声场的分布会发生一些变化，虽然近场距离、主声束范围不变，但接收端的声压值明显不同，如图5所示，声波频率设置为50 kHz时，衰减系数越大，接收的声压值越小,符合式(7)。

图5 不同衰减系数下的声压分布

由图4、图5看出：在一定声波频率下，如50 kHz时，探头的摆放位置不应置于-11，11 cm处，由于即使流体参数变化引起衰减系数改变，但此点的声压值一直为0 Pa，无法从中获取流体的有效信息，另外，声能量主要集中在主声束，为了获得更高的精确度，探头应尽量靠近主轴。而且在多探头测量时，在主声束范围无法容纳多个探头的情况下，可以将探头安置在副声束的峰值附近，以获得较好的声信号。

3 结 论

管道壁上的声压分布与声波频率和衰减系数有关，且非定值，具有一定分布规律。主声束范围内声压在中心处最高，越偏离中心声压值越小。偏离主轴声压成波浪形变化，且在某些点处声压值为零。因此，当用超声波探头接收信号时，应该尽量避开零点且选取信号较强的区域，以获得精确度比较高的信号。

[1] 张向珂,张世庆,闻凤连,等.高精度相位法超声测距系统研究[J].传感器与微系统,2010,29(2):45-47.

[2] 薛明华.超声法测量颗粒两相流粒径及浓度的理论及实验研究[D].上海：上海理工大学,2008.

[3] 蔡小舒,苏明旭,沈建琪，等.颗粒粒度测量技术及应用[M].北京：化学工业出版社,2010.

[4] 李永明,苏明旭,袁安利,等.基于超声的管道内粉体体积分数的测量[J].中国科学院大学学报,2016,33(2):277-282.

[5] 许肖梅.声学基础[M].北京:科学出版社,2003.

[6] 乔 榛.超声法一次风流速和煤粉浓度在线测量研究[D].南京：南京理工大学,2013.

[7] 严祯荣,罗晓明,侯怀书.气力输送小流量煤粉在线流量超声测量[J].洁净煤技术,2015(2):122-124.

[8] 邹 伟,李 丽,王 秀,等.超声波传感器测距实验平台设计与实验[J].传感器与微系统,2011,30(10):89-92.

[9] Khatchikian P,Riebel U,Kräuter U.Phase velocity of ultrasound in suspensions of large particles[J].Acta Acustica United with Acustica,1999,85(6):800-808.

[10] 东鑫渊,谷立臣,琚晓涛.超声谐振器在传感器测距中应用分析[J].传感器与微系统,2014,33(1):157-160.