裂纹参数和筋条布局对共振九宫板动态应力强度因子的影响

刘双燕，李玉龙，薛璞，石霄鹏

西北工业大学 航空学院 航空结构工程系 先进结构和材料研究所，西安 710072

由于质量限制，飞行器外壳一般设计为轻质的薄壁加筋结构。在服役过程中，这些结构会不可避免地受到气动载荷的激励而发生共振并出现疲劳破坏[1]。Pairs准则表明：线弹性范围内，裂尖应力强度因子(SIF)的幅值决定了该裂纹的扩展速率[2]。因此研究共振状态下典型薄壁加筋结构中裂纹参数对裂尖应力强度因子的影响，对预测裂纹的扩展行为和结构的疲劳寿命有显著的理论和工程应用意义。

九宫板由壁板和呈“井”字型分布的筋构成，作为一种典型的薄壁加筋结构在飞行器中被广泛采用。大量学者对九宫板的力学行为进行了研究，然而他们主要关注于该结构的屈曲行为[3-8]和承载能力[9-12]性能的分析，很少研究该结构在振动载荷下的力学行为。刘双燕等[13]在九宫板表面覆盖阻尼结构并进行相应优化，研究了该结构在振动载荷下的力学响应。由于没有考虑裂纹，上述文献中的结论不能完全适用于含裂纹的九宫板。因此，九宫板动态应力强度因子的计算方法、过程以及裂纹参数(偏转角度和裂纹长度)对其最大值的影响还需进一步的研究。

对于平板上的裂纹，如果包含理想边界条件，能计算出裂尖动态应力强度因子的理论解[14-15]；对于加筋薄壁结构上的裂纹，其动态应力强度因子很难用理论方法进行计算，通常采用有限元方法求解。振动载荷为持续载荷，其很长的作用时间导致求解结构中裂尖应力强度因子需要耗费大量机时。为了简化振动工程问题中的计算，Doyle和Rizzi[16]首次提出计算动态应力强度因子的模态叠加法：线弹性振动中，应力强度因子的响应类似于振幅的模态响应，为频率的函数。Galenne等[17]进一步表明：该模态方法可以快速精确地求解低频振动结构的Ⅰ型动态应力强度因子，并在蒸汽轮机叶片的振动分析中得到证实。Albuquerque等[18]将应力强度因子模态叠加法与子模型法结合，对简支梁的振动响应进行了计算，发现该方法既不损失计算精度又能显著提高计算效率。Tran等[19]将应力强度因子模态叠加法和扩展有限元方法结合，并应用于求解简单结构中三维裂纹的扩展，得到了精确的计算结果。以上文献表明结合有限元和模态叠加法能够准确、快速地求解复杂振动结构中裂纹的Ⅰ、Ⅱ和Ⅲ型动态应力强度因子。

本文用有限元分析软件ABAQUS®对九宫板在不同裂纹偏转角度(0°、30°、45°、60°和90°)及长度(30、60、90、120和150 mm)下进行模态分析，提取了裂纹面节点前8阶的模态位移并计算得到了Ⅰ、Ⅱ及Ⅲ型裂纹的模态应力强度因子，然后利用模态叠加法计算出裂纹在共振条件下的应力强度因子。分析了裂纹参数(偏转角度和长度)及筋条布局对应力强度因子和裂纹类型的影响。

1 基础理论

1.1 模态分析

经典黏性阻尼系统的n维自由度线性振动微分方程为

(1)

在简谐激励力f(t)=f0ejω t作用下，有简谐响应x(t)=x0ejω t，x0为响应幅值。则有[20]

(2)

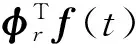
(3)

式中：mr、kr、ωn r和φr分别为r阶模态质量、模态刚度、模态频率和模态振型；cr和ξr分别为r阶模态阻尼和模态阻尼比。

对于线性系统而言，若系统的输入为单一正弦波，即

f(t)=f0sin(ωt)=f0Im(ejω t)

(4)

则系统的稳态输出为

x(t)=Im(x(t))=

(5)

那么相应的纯模态响应为

(6)

1.2 应力强度因子的快速求解算法

动态线性问题的位移x(s,t)可以近似地表示为

(7)

式中：φr(l)为模态变换矩阵(模态振型)，仅与结构的边界和几何条件l有关；ar(t)为模态坐标，即上文所说的模态响应，也称为模态参与系数；m为截断模态阶数，模态叠加法的计算精度取决于m的取值。

在线弹性断裂问题中，裂纹尖端位移场可以通过应力强度因子KⅠ、KⅡ和KⅢ来描述。在裂尖M点处建立(N，T，V)笛卡儿坐标系，其中N为裂纹切平面的法线方向，T为裂尖曲线的切向方向，V为裂纹前缘局部内法线方向。KⅠ、KⅡ和KⅢ的表达式[21]为

(8)

式中：E为板的弹性模量；υ为泊松比；R为在(N，T)平面上计算点到裂纹尖端的距离；s为沿着裂纹前缘的曲线横坐标；xN(R,s,t)、xT(R,s,t)和xV(R,s,t)分别为t时刻与裂纹尖端距离为R、沿裂纹前缘曲线横坐标s的节点位移分别在N、T和V方向上的投影值。

结合式(7)和式(8)，可得

(9)

(10)

需要注意的是，在实际应用中应忽略裂纹的闭合效应，当计算得到的KⅠ(s,t)<0时，人为设定其为0[17]。

（1）优化数据信息的获取方式是充分挖掘与利用数据价值的重要基础，能够逐步实现信息获取方式的智能化，不断提升数据质量、完善数据资源种类。随着科技水平的不断提高，无人机以及遥感等新型技术也日趋成熟。电网规划设计部门可以利用遥感技术直接获取数据，再根据具体的需求来绘制平面地图或3D地图，与直接获取卫星地图相比，这一方法可以提高原始数据的精确度并实现数据的充分利用。

对于给定载荷的结构线性动力学响应问题，选取前n阶特征模态，求解应力强度因子可以通过下面两步来进行：

步骤1对结构进行模态分析，根据式(10)识别前n阶模态应力强度因子，其为仅与结构几何参数和边界条件有关而与载荷无关的量，只需要计算一次。

步骤2根据式(3)求得结构的模态坐标，并结合式(9)，进一步求解与时间有关的应力强度因子。

1.3 准确性验证

Galenne等[17]采用该快速解算方法计算了含裂纹梁在弯曲振动时的应力强度因子，发现选取的模态数量超过8阶后应力强度因子的计算误差将小于1%。因此本文中九宫板振动时应力强度因子的计算也选取前8阶模态。

虽然该快速解算方法能准确求解梁弯曲振动时的应力强度因子，但是仍然不确定该方法能否准确求解板壳振动时的应力强度因子。为此，在商用有限元软件ABAQUS®中建立了和姜伟等[22]的研究中相同尺寸、材料和载荷的平板模型用于计算的验证。平板的长度、宽度和厚度分别为40、20和1 mm，并包含一条长度为4.8 mm的中心穿透裂纹。裂纹采用Seam建模，裂纹尖端附近区域内最小网格尺寸取0.1 mm，远离裂纹尖端的区域为边长为1.5 mm的四边形单元。板的弹性模量为200 GPa，泊松比为0.3,密度为5 000 kg/m3。在平板的宽度边上施加P(0)=10 MPa的阶跃动态拉伸载荷，载荷时长为14 μs。与姜伟等[22]的结果相比较，采用该快速解算方法计算得到的应力强度因子的最大误差为4.7%。

2 有限元模型及求解过程

2.1 有限元建模

含中心裂纹九宫板结构的示意图如图 1 所示。平板尺寸为900 mm×700 mm×1.6 mm，筋条间距d=204.5 mm，对称布放，筋条截面形状为Z型，筋厚度为3.5 mm，其平面尺寸如图1(b)所示；在筋交汇点处用L型角片(如图 1(a)中A处)连接，每个筋条的端部与2个条形角片(如图 1(a)中B处)固定连接，2种角片厚度均为2 mm。

九宫板结构的平板、筋条及角片均为2024-T3铝合金，其材料性能如表1所示。

图1 含中心裂纹九宫板示意图
Fig.1 Diagram of 3×3 grid stiffened panel with center crack

-
-

ParameterDensity/(kg·m-3)Elasticmod-ulus/GPaPoissonratioValue2780700.346

在有限元模拟中，裂纹长度为2a、偏转角度为φ的九宫板中的平板四边采用固支的边界条件，九宫板中突出的方形角片部分采用简支的边界条件。

图2 九宫板模型网格
Fig.2 Mesh of 3×3 grid stiffened panel model

在网格划分中，中心裂纹尖端采用三角形壳单元，其余部分结构(面板、筋条和角片)均采用4节点缩减积分壳单元。研究表明，当裂纹尖端附近区域节点的最小间距小于0.04a时，裂纹尖端应力场的奇异性对计算结果的影响[21, 23-25]可以忽略。在本文的计算中，九宫板裂纹长度2a=30 mm，裂纹尖端区域节点的间距小于0.6 mm，奇异性影响可以忽略。裂纹采用Seam建模，裂纹尖端附近区域内网格尺寸取0.2 mm。模型的全局网格尺寸为5 mm，总节点数为36 745，单元数为35 231，网格无畸变。模型全局网格如图2所示，其中内插图为裂纹尖端区域T的局部放大图。另外，就网格尺寸的无关性也进行了比较分析，2、5 和10 mm的计算结果表明，其误差小于1%。

2.2 应力强度因子的求解过程

本节以裂纹长度2a=30 mm、偏转角度φ=0°的九宫板模型为例来描述采用1.2节所述的快速求解算法的计算过程。该九宫板结构的前8阶模态频率和振型如图3所示。

从图3可以看出，九宫板中心区域的2、4、5和7阶模态位移为0，而1、3、6和8阶模态振型均关于面板的轴线对称。由式(10)可知，面板中心裂纹的前8阶Ⅱ、Ⅲ型模态应力强度因子应该为0，I型模态应力强度因子结果如图4所示。

在九宫板表面施加垂直于面板的面压载荷P=sin(ωt)，幅值为1 Pa，ω为结构的1阶模态圆频率；t为共振作用时间，文中取为1 s。结构的振动形式为垂直于面板的定常强迫振动，与其1阶模态振型类似。结构的模态阻尼系数取为0.005[26]。根据式(3)可求得前8阶模态的参与系数ar，图5给出了结构1阶模态参与系数a1随时间的变化曲线。

然后，将求得的各阶模态应力强度因子及其参与系数代入式(9)，可以得出对应的KⅠ(t)，如图6所示。可以看出，在共振条件下，当阻尼很小时，裂纹尖端的应力强度因子波动幅值逐渐增大至恒定值Kmax。

在动态断裂问题中，应力强度因子的幅值是要关注的问题，因此，在第3节的讨论中，关注裂纹尖端的应力强度因子的最大值Kmax。

图3 前8阶模态频率和模态振型(2a=30 mm, φ=0°)
Fig.3 The first eight mode frequencies and mode shapes (2a=30 mm, φ=0°)

图4 前8阶Ⅰ型模态应力强度因子(2a=30 mm, φ=0°)
Fig.4 The first eight mode stress intensity factors of Mode Ⅰ(2a=30 mm,φ=0°)

图5 1阶模态参与系数随时间的变化曲线 (2a=30 mm,φ=0°)
Fig.5 Variation curve of the first mode contribution factors with time (2a=30 mm,φ=0°)

图6 Ⅰ型应力强度因子随时间的变化曲线 (2a=30 mm,φ=0°)
Fig.6 Variation curve of stress intensity factor of Mode Ⅰ vs time (2a=30 mm,φ=0°)

3 裂纹参数对应力强度因子的影响

通常地，裂纹参数会影响结构的刚度和固有频率。对于本文所研究的九宫板结构，中心穿透裂纹对其刚度和固有频率的影响较小，但对模态振型影响很大。裂纹参数(偏转角度和长度)不同时，裂纹尖端位移场及其应力强度因子差别很大。因而本节利用1.2节所介绍的快速算法考虑不同的裂纹偏转角度(φ=0°、30°、45°、60°和90°)和裂纹长度(2a=30，60，90，120，150 mm)对九宫板应力强度因子最大值Kmax的影响。

3.1 裂纹偏转角度的影响

当裂纹长度为30和150 mm时，九宫板的Kmax随裂纹偏转角度的变化曲线如图7所示。

从图7(a)可以看出，当裂纹长度为30 mm时，KⅠ,max随着偏转角度的增大而增大。图8给出了裂纹长度为30 mm、偏转角度为45°时，九宫板结构的1阶模态振型图。由图8可知，裂纹周边的位移近似为椭圆形分布，且其长轴平行于0°方向。当裂纹偏转角度为0°和90°时，其KⅡ和KⅢ为0。当偏转角度为30°、45°和60°时，结构不再关于面板轴线对称。共振时，裂纹尖端面板法向位移必然不同步，沿面板法向出现位移差(撕裂位移)，因而存在Ⅲ型裂纹，如图7(a)所示。当偏转角度为45°时，其撕裂位移最大，故其KⅢ,max最大。KⅢ,max随着偏转角度的增大先增大再减小。

由不同类型的Kmax可以看出，当裂纹偏转角度从0°增大到90°时，KⅠ,max均远大于KⅡ,max和KⅢ,max，裂纹类型以Ⅰ型为主。

图7 2a=30，150 mm时应力强度因子最大值 随偏转角度的变化曲线
Fig.7 Variation curves of maximum values of stress intensity factor vs inclined angles for 2a=30,150 mm

类似地，当裂纹长度为150 mm时，如图7(b)所示，不同类型的应力强度因子随着偏转角度的增大变化趋势不变。当裂纹偏转角度为0°～90°时，KⅠ,max显著增大，当偏转角度为30°、45°和60°时，KⅢ,max也显著增大。当裂纹偏转角度为0°和90°时，裂纹以Ⅰ型为主。当偏转角度为30°、45°和60°时，裂纹类型以Ⅰ和Ⅲ混合型为主。图9给出了裂纹长度为150 mm、裂纹偏转角度为45°时，九宫板结构的1阶模态振型图，内插图为裂纹尖端T处的局部振型放大图。比较图8和图9(两图的标尺相同)，可以明显看出当裂纹长度2a=150 mm时，沿面板法向出现的位移差较大，即Ⅲ型裂纹存在且其Kmax较大。

图8 九宫板的1阶模态振型(2a=30 mm, φ=45°)
Fig.8 The first mode shape of 3×3 grid stiffened (2a=30 mm, φ=45°)

图9 九宫板的1阶模态振型(2a=150 mm,φ=45°)
Fig.9 The first mode shape of 3×3 grid stiffened panel (2a=150 mm, φ=45°)

由此可见，对于同样的裂纹偏转角度，当裂纹长度不同时，其裂纹类型也可能不同。因此很有必要进一步讨论裂纹长度对其应力强度因子的影响。

3.2 裂纹长度的影响

图10给出了裂纹偏转角度为0°～90°时，应力强度因子最大值Kmax随裂纹长度的变化曲线。

从图10 可以看出，当裂纹偏转角度不变时，KⅠ,max随着裂纹长度的增大而增大。当裂纹偏转角度为30°、45°和60°时，KⅢ,max随着裂纹长度的增大而增大。当裂纹长度从0 mm增大到90 mm时，裂纹类型以Ⅰ型为主；当裂纹长度为120和150 mm时，裂纹类型为Ⅰ、Ⅲ混合型。其原因在于在共振条件下，当阻尼很小时，随着裂纹长度的增大，裂纹面两侧的非对称性撕裂位移迅速增大。

图10 不同偏转角度时应力强度因子最大值 随裂纹长度的变化曲线
Fig.10 Variation curves of maximum values of stress intensity factor vs crack length at various inclined angles

4 筋条布局对应力强度因子的影响

为了研究筋条布局对含中心裂纹九宫板结构应力强度因子的影响，改变图 1(a)中纵向筋条的间距d，使得筋条间距比r分别为0.33、0.67和1.00。取裂纹长度为30 mm，偏转角度为30°、45°和60°。图11给出了九宫板Kmax随裂纹偏转角度的变化曲线，不同筋条布局下的1阶振型如图12所示。

当r=1.00时，裂纹偏转角度从30°增加到60°，裂纹附近区域1阶模态振型位移分布均近似为圆形，如图12(c)所示，其KⅠ,max基本不变，KⅢ,max基本为0(如图11所示)，因此裂纹类型为Ⅰ型。

当r=0.33时，KⅠ,max随偏转角度的增大而增大，KⅢ,max相对KⅠ,max不可忽略，裂纹类型为Ⅰ、Ⅲ混合型。

当r=0.67时，KⅠ,max随偏转角度的增大而增大，KⅢ,max相对较小，裂纹类型以Ⅰ型为主。当r=0.67时，同样的裂纹偏转角度下，KⅠ,max远大于r=0.33时的值。这是由于当r=0.67时结构刚度较大，在同样载荷作用下，其在裂纹表面释放的能量较大。随着裂纹偏转角度增大，r=0.67时结构的KⅠ,max大于r=1.00时的值。这是由于当r=1.00时，其局部振动位移峰值主要分布在横向筋条间的3个区域，如图12(c)所示，导致在同样的共振载荷作用下，其裂纹表面释放的能量较小。

图11 不同筋条布局下应力强度因子最大值 随裂纹偏转角度的变化曲线
Fig.11 Variation curves of maximum values of stress intensity factor vs inclined angles with different stiffener layouts

图12 当筋条布局为r=0.33，0.67，1.00时的1阶振型(2a=30 mm, φ=45°)
Fig.12 The first mode shape with stiffener layout of r=0.33, 0.67, 1.00 (2a=30 mm, φ=45°)

5 结 论

采用所提出的求解方法能快速准确地计算包含中心穿透裂纹九宫板的动态应力强度因子。讨论了筋条间距、裂纹角度和长度对动态应力强度因子的影响，得到如下结论：

1) 当裂纹九宫板为不对称结构时，即裂纹偏转角度不等于0°和90°时，对于不同的筋条间距、裂纹偏转角度和长度，中心穿透裂纹类型均为Ⅰ、Ⅱ和Ⅲ混合型，但以Ⅰ型裂纹为主导。

2) Ⅰ型应力强度因子随着裂纹偏转角度或长度的增加几乎线性地增加，但是对裂纹长度更加敏感。

3) 九宫板的筋条间距能显著影响其振动模态，从而导致应力强度因子的变化。筋条间距比r=1.00(九宫板中心区域为正方形)时，其应力强度因子最小。

致 谢

感谢李涛博士和于霞博士对本论文的精心修改。

[1] 姚起杭, 姚军. 工程结构的振动疲劳问题[J]. 应用力学学报, 2006, 23(1): 12-15.

YAO Q H, YAO J. Vibration fatigue in engineering structures[J]. Chinese Journal of Applied Mechanics, 2006, 23(1): 12-15 (in Chinese).

[2] PAIRS P C, GOMEZ M P, ANDERSON M E. A rational analytical theory of fatigue[J]. Trends in Enginneering, 1961, 13: 9-14.

[3] 张浩宇, 何宇廷, 冯宇, 等. 先进复合材料薄壁加筋板轴压屈曲特性及后屈曲承载性能[J]. 航空材料学报, 2016, 36(4): 55-63.

ZHANG H Y, HE Y T, FENG Y, et al. Buckling and post-buckling performance of advanced composite stiffened panel under compression[J]. Journal of Aeronacutical Materials, 2016, 36(4): 55-63 (in Chinese).

[4] 王燕, 李书, 许秋怡, 等. 复合材料加筋板剪切后屈曲分析与优化设计[J]. 航空学报, 2016, 37(5): 1512-1525.

WANG Y, LI S, XU Q Y, et al. Optimization design and analysis of stiffened composite panels in post-buckling under shear[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(5): 1512-1525 (in Chinese).

[5] KUMAR Y V S, PAIK J K. Buckling analysis of cracked plates using hierarchical trigonometric functions[J]. Thin-Walled Structures, 2004, 42(5): 687-700.

[6] LEI Z, BAI R, TAO W, et al. Optical measurement on dynamic buckling behavior of stiffened composite panels under in-plane shear[J]. Optics and Lasers in Engineering, 2016, 87: 111-119.

[7] MOUHAT O, ABDELLATIF K. Dynamic buckling of stiffened panels[J]. Procedia Engineering, 2015, 125: 1001-1007.

[8] 王博, 田阔, 郑岩冰, 等. 超大直径网格加筋筒壳快速屈曲分析方法[J]. 航空学报, 2017, 38(2): 220379.

WANG B, TIAN K, ZHENG Y B, et al. A rapid buckling analysis method for large-scale grid-stiffened cylindrical shells[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(2): 220379 (in Chinese).

[9] PAIK J K, SATISH KUMAR Y V, LEE J M. Ultimate strength of cracked plate elements under axial compression or tension[J]. Thin-Walled Structures, 2005, 43(2): 237-272.

[10] CUI C, YANG P, LI C, et al. Ultimate strength characteristics of cracked stiffened plates subjected to uniaxial compression[J]. Thin-Walled Structures, 2017, 113: 27-38.

[11] SHI X H, ZHANG J, GUEDES SOARES C. Experimental study on collapse of cracked stiffened plate with initial imperfections under compression[J]. Thin-Walled Structures, 2017, 114: 39-51.

[12] 陈安, 魏玉龙, 廖江海, 等. 机身加筋壁板复合加载损伤容限性能试验[J]. 航空学报, 2017, 38(1): 420093.

CHEN A, WEI Y L, LIAO J H, et al. Damage tolerance test of stiffened fuselage panel under complex load[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 420093 (in Chinese).

[13] 刘双燕， 李玉龙， 邓琼, 等. 基于ESO法的九宫板阻尼结构的优化设计方法[J]. 振动与冲击, 2016, 35(22): 197-203.

LIU S Y, LI Y L, DENG Q, et al. Topological optimization design of 3×3 grid stiffened panel with additional damping layers based on evolutionary structural optimization[J]. Journal of Vibration and Shock, 2016, 35(22): 197-203 (in Chinese).

[14] 中国航空研究院. 应力强度因子手册[M]. 北京: 科学出版社, 1981: 1-30.

Chinese Aeronacutical Establishment. Stress intensity factor handbook[M]. Beijing: Science Press, 1981： 1-30 (in Chinese).

[15] 程靳， 赵树山. 断裂力学[M]. 北京: 科学出版社, 2014: 57-82.

CHENG J, ZHAO S S. Fracture mechanics[M]. Beijing: Science Press, 2014: 57-82 (in Chinese).

[16] DOYLE J F, RIZZI S A. Frequency domain stress intensity calibration of damped cracked panels[J]. International Journal of Fracture, 1993, 61(2): 123-130.

[17] GALENNE E, ANDRIEUX S, RATIER L. A modal approach to linear fracture mechanics for dynamic loading at low frequency[J]. Journal of Sound and Vibration, 2007, 299(1-2): 283-297.

[18] ALBUQUERQUE C, CASTRO P, CALCADA R. Efficient crack analysis of dynamically loaded structures using a modal superposition of stress intensity factors[J]. Engineering Fracture Mechanics, 2012, 93: 75-91.

[19] TRAN V X, GENIAUT S, GALENNE E, et al. A modal analysis for computation of stress intensity factors under dynamic loading conditions at low frequency using eXtended finite element method[J]. Engineering Fracture Mechanics, 2013, 98: 122-136.

[20] 邱吉宝， 向树红， 张正平. 计算结构动力学[M]. 合肥: 中国科学技术大学出版社, 2009： 181-182.

QIU J B, XIANG S H, ZHANG Z P. Computational structural dynamics[M]. Hefei: University of Science and Technology of China Press, 2009: 181-182 (in Chinese).

[21] HAN Q, WANG Y, YIN Y, et al. Determination of stress intensity factor for mode I fatigue crack based on finite element analysis[J]. Engineering Fracture Mechanics, 2015, 138: 118-126.

[22] 姜伟, 杨平, 董琴. 平板穿透裂纹尖端动态应力强度因子研究[J]. 武汉理工大学学报(交通科学与工程版), 2016, 40(5): 820-825.

JIANG W, YANG P, DONG Q. Research on dynamic stress intensity factors for through-cracked plates[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering),2016, 40(5): 820-825 (in Chinese).

[23] ZHU W X, SMITH D J. On the use of displacement extrapolation to obtain crack tip singular stresses and stress intensity factors[J]. Engineering Fracture Mechanics, 1995, 51(3): 391-400.

[24] GUINEA G V, PLANAS J, ELICES M.KIevaluation by the displacement extrapolation technique[J]. Engineering Fracture Mechanics, 2000, 66(3): 243-255.

[25] QIAN G, GONZLEZ-ALBUIXECH V F, NIFFENEGGER M, et al. Comparison ofKIcalculation methods[J]. Engineering Fracture Mechanics, 2016, 156: 52-67.

[26] 戴德沛. 阻尼减振降噪技术[M]. 西安: 西安交通大学出版社, 1986: 16.

DAI D P. Damping technology in vibration and noise reduction[M]. Xi’an: Xi’an Jiaotong University Press, 1986: 16 (in Chinese).