简谐力激励下多组件结构系统的整体优化设计

朱继宏，赵华，刘涛，张卫红

1.西北工业大学 航宇材料结构一体化设计与增材制造装备技术国际联合研究中心，西安 710072 2.西北工业大学 金属高性能增材制造与创新设计工信部重点实验室，西安 710072 3.西北工业大学 无人系统技术研究院-智能材料与结构研究所，西安 710072

自从Bendsøe和Kikuchi[1]在1988年首次提出均匀化方法以来，拓扑优化就一直被认为是结构概念设计阶段非常有效的方法。目前，拓扑优化在理论研究和实际应用中都获得了显著的进步[2-4]。尤其是在航空航天领域，拓扑优化对于提高结构性能，减轻结构重量具有十分重要的意义。然而，在实际结构中常见的多组件结构系统的优化设计仍然是一个充满挑战的问题。

典型的多组件结构系统主要包括支撑结构及其上面具有特定功能的组件。其中，组件通过铆钉或螺栓等连接件与支撑结构连接成为一个整体。这类结构广泛存在于机械、汽车以及航空航天等领域。

最初，多组件结构系统的优化设计是在固定组件位置的情况下，只对支撑结构进行优化[5-6]。为了克服组件无法移动的问题，朱继宏等[7]提出一种对支撑结构构型和组件位置同时优化的方法。同时，这也带来组件间的位置干涉和支撑结构与组件间的有限元模型连接问题。针对这类问题，Qian和Ananthasuresh[8]提出过一种通过指数函数描述组件几何形状来实现多组件系统布局优化的方法。亢战等[9]发展了基于水平集的非干涉约束方法，并将其应用到结构拓扑和可移动空洞的协同优化中。张维生等[10]提出基于结构骨架的水平集方法去控制嵌入式组件间的最小和最大距离。朱继宏等[11]提出的有限包络圆法(FCM)和多点约束(MPC)方法，由于可靠和易实现而被本文所采用。目前多组件结构系统整体优化的研究主要针对结构的静力学性能，而忽视了考虑结构的动力学性能。

在结构动力学优化设计中，相关研究主要关注结构动态特性和动响应两类问题。Pedersen[12]、Du[13]和Tsai[14]等学者在提高结构动态特性方面做了有效的研究工作，比如最大化结构的特征频率或使特征频率远离激励频率等。事实上，相较于提高结构的动态特性，优化结构的动响应能够更加直接地提高结构的动力学性能。Ma[15]、Jog[16]和Shu[17]等通过不同的方法在结构简谐激励下的动柔顺度和位移响应优化方面作了富有成效的研究。在结构动响应求解方面，Yoon[18]、Besselink[19]和Liu[20]等分析比较了不同方法的优缺点。其中，模态加速度法(MAM)对于大规模自由度优化问题在求解精度和效率方面有很好的表现。

在结构整体设计和动力学拓扑优化两个方面尽管已经分别有相应的研究[21-22]，但结构在动力学激励下的整体优化方面仅有很少一部分研究内容。张桥等[23]对静力和随机激励下的多组件结构系统的整体优化问题进行了研究，由于采用密度点和网格嵌入技术而无法模拟螺栓等常用连接形式。

实际工程中多组件结构系统往往会由于结构不平衡产生简谐激励和各种周期性载荷，而这些周期性载荷可以通过傅里叶变换转化为不同频率下简谐激励的叠加。因此，研究结构简谐载荷下的整体优化问题将变得很有意义。

1 整体优化的基础公式

1.1 几何约束

为了避免优化过程中组件与组件之间产生重叠，并且保证组件始终位于支撑结构区域内，本文中引入FCM作为几何约束。所谓FCM就是利用一系列圆去近似组件的轮廓和设计域的边界(如图1)。这样，将模型的几何约束转化为包络圆间的非干涉约束，而非干涉约束可以通过式(1)获得，同时其灵敏度也能够轻松求解得到。

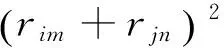
(1)

式中：(xim,yim)和rim为第i个组件的第m个包络圆的圆心坐标和半径；(xjn,yjn)和rjn为第j个组件的第n个包络圆的圆心坐标和半径；gk为第k个非干涉约束值。

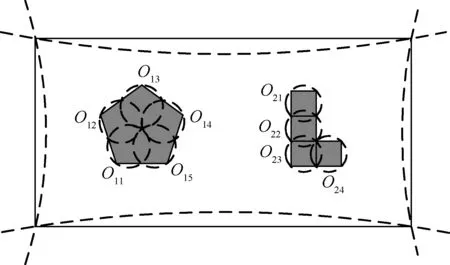
图1 有限包络圆近似组件和设计域边界Fig.1 FCM approximation for components and design domain boundary

1.2 MPC方法

MPC方法广泛应用在模拟连接、对称边界条件以及网格强制兼容方面[24]。本文采用的MPC方法不同于传统组件节点与支撑结构节点间直接连接的形式，而是通过单元形状函数建立组件节点与支撑结构单元上某处的位移约束，具体描述如图2所示。

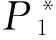
(2)

实际上，MPC方程节点是位移的线性组合。当有多个MPC连接节点时，MPC方程可以写为

Hu=0

(3)

图2 多点约束方法的定义Fig.2 Definition of MPC method

式中：H为由参与构成MPC连接的节点坐标和单元形状函数决定的系数矩阵；u为多组件结构系统的总体位移矢量。

1.3 多组件结构系统的简谐响应分析

考虑到多点约束，通过引入拉格朗日乘子建立修正的线性系统动平衡方程[25]为

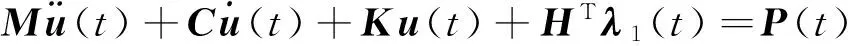
Hu(t)=0

(4)

式中：M、C和K分别为结构系统的整体质量矩阵、阻尼矩阵和刚度矩阵；u(t)为结构整体位移向量；P(t)为外部简谐载荷，且P(t)=Pejωpt(j2=-1)，P和ωp分别为载荷幅值和频率；λ1(t)为拉格朗日乘子。

在采用模态叠加法求解简谐响应时，可以通过求解自由振动下的平衡方程式(5)获得结构的特征值和特征频率。

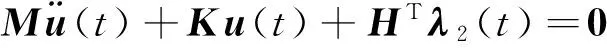
Hu(t)=0

(5)

式中：λ2(t)为拉格朗日乘子。结构的第i阶圆频率ωi和特征向量Φi可以通过求解自由振动系统的参数方程式(6)得到。

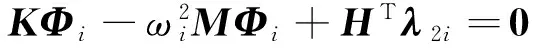
HΦi=0

(6)

式(6)可以写成块矩阵的形式，即

(7)

假设

(8)

因此，式(7)可以写为

(9)

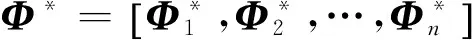
{Φ*TM*Φ*=I

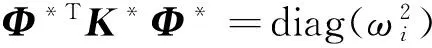
(10)

假设系统的瑞利阻尼矩阵是质量矩阵和刚度矩阵的线性组合，即

C=αM+βK

(11)

式中：α和β为瑞利阻尼系数，本文中取α=10-2，β=10-5。将式(10)展开，可以得到

(12)

式中：ξi为第i阶阻尼系数，可以通过式(13)求解得到。

(13)

通过引入广义坐标，位移响应可以写为

u(t)=Φy(t)

(14)

(15)

(16)

因此

(17)

通过模态位移法(MDM)可以求得

(18)

考虑到计算效率，求解中只取结构前l阶模态叠加，即

(19)

对于大规模自由度问题的求解，MDM由于只考虑了低阶模态，使得求解精度无法满足要求。而MAM在求解精度和效率之间取得很好的平衡，下面对MAM进行推导。

解耦的运动方程式(16)可以写为

(20)

将式(20)代入式(19)可得

(21)

通过使式(18)中ωp=0,可以得到结构的静力分析结果为

联合收割机的使用季节性强，闲置时间长。要保持收割机良好的技术状态，有效地延长其使用寿命，闲置阶段的优质保养非常重要。

(22)

式中：usd可以直接通过式(23)求解。

{Kusd+HTλ3=P

Husd=0

(23)

综合式(20)～式(22)可以得到通过MAM求解的结构位移响应为

(24)

并且，将式(22)代入式(24)可以得到

(25)

式(25)右边第2项相当于对MDM求解结果的修正。

假设a是除s项为1其余项均为0的列向量。那么，目标自由度的位移可以表示为

us(t)=aTu(t)

(26)

进而，目标自由度的位移幅值可以表示为

(27)

式中：Xs为目标自由度位移的复数形式;Re(Xs)和Im(Xs)分别为Xs的实部和虚部。

2 整体优化问题数学模型

在多组件结构系统整体优化设计中，以目标自由度的位移响应幅值最小为优化目标。另外，包含两类设计变量，即控制组件位置的几何设计变量和控制支撑结构构型的拓扑设计变量，以及3个约束条件：控制结构优化后质量的体积约束、实现组件与支撑结构间连接的MPC约束和FCM的非干涉约束，以数学模型形式可以表示为

(28)

式中：ηh为单元h的伪密度设计变量；Nd为设计单元的个数；ζjx、ζjy、ζjθ为第j个组件位置和转角的几何设计变量；Nc为组件的个数；Ng为非干涉约束的个数；V和V0分别为设计域的体积分数及其上限值。为了防止结构质量矩阵、刚度矩阵和阻尼矩阵出现奇异，给伪密度设置一个下限值η0=0.001。

2.1 材料插值模型

实体各向同性微结构惩罚(SIMP)模型是经典的材料插值模型，由Bendsøe和Sigmund[26]提出。但在动力学分析中，SIMP模型会导致局部模态问题[27]。针对这种问题，Sotlpe[28]和笔者团队[29]分别采用了材料属性有理近似(RAMP)模型和多项式插值(PIS)模型。在本文中，采用PIS模型,即

(29)

式中：mh和kh分别为单元h的质量矩阵和刚度矩阵；mh0和kh0为单元h在实体材料下的质量矩阵和刚度矩阵。

2.2 灵敏度分析

将式(17)代入式(24)可得

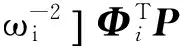
(30)

假设

(31)

那么，式(30)可以简化为

(32)

进而，结构的位移响应关于设计变量的偏导数可以表示为

(33)

通过伴随法[30]求解得到目标自由度静力分析位移us(sd)对设计变量的偏导为

(34)

式中：λa为拉格朗日乘子；Λ为伴随矢量，且满足a=KΛ。

由于H与伪密度设计变量ηh无关，因此

(35)

另外，当组件在支撑结构上移动时，系统的刚度矩阵和质量矩阵不发生改变，因此

{∂K/∂ρ=0

∂M/∂ρ=0ρ=ζjxorζjy

(36)

但是，当组件在支撑结构上转动时，系统的刚度矩阵和质量矩阵将发生改变，并且与初始的刚度矩阵和质量矩阵满足

(37)

式中：Kd、Kcj、Md和Mcj分别为支撑结构和第j个组件初始的刚度矩阵和质量矩阵；Aj为第j个组件的刚度和质量变换矩阵。

经过进一步推导，us(sd)关于不同设计变量的偏导可以表示为

(38)

针对式(33)剩余部分偏导的求解，需要用到特征值和特征向量关于设计变量的偏导。因此，通过求解式(6)关于设计变量的偏导，可以求得

(39)

(40)

(41)

联合式(6)、式(40)和式(41)可得

(42)

进一步求解和化简后可以得到

(43)

相应的特征向量关于设计变量的偏导数可以表示为[21]

(44)

式中：

当i≠r时

βi r=

(45)

当i=r时

(46)

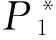
(47)

而

{xglobal=ζjx+xlocalcosζjθ-ylocalsinζjθ

yglobal=ζjy+xlocalsinζjθ+ylocalcosζjθ

(48)

式中：(xlocal,ylocal)为P1在组件局部坐标系下的坐标。

由于矩阵Aj由与ζjθ相关的坐标变换矩阵组装而成，因此，Aj对设计变量ζjθ的偏导数实际是矩阵各分量中三角函数对ζjθ的导数。

最后，可以通过下面的链式法则求解目标自由度位移幅值关于设计变量的灵敏度。

(49)

3 数值算例

3.1 带组件的悬臂梁结构

3.1.1 给定频率下的简谐力激励

如图3(a)所示，大小为1.2 m×0.6 m的矩形支撑结构,左端固定，上面有3个不同组件，每个组件的尺寸和MPC节点位置如图3(b)所示。将支撑结构划分为80×40的壳单元网格，并在其右下角节点处施加幅值为5 kN的简谐力，支撑结构和组件采用相同的材料参数，具体见表1。

以载荷施加节点处竖直方向的位移响应幅值最小为优化目标，并对优化模型施加非干涉约束和40%的体积分数上限约束。采用移动渐近线全局收敛算法(GCMMA)来求解该优化问题。

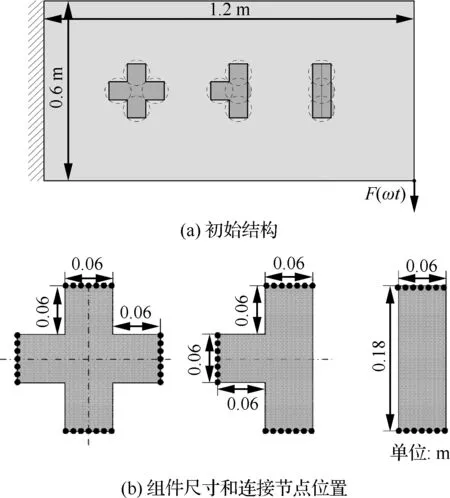
图3 简谐力激励下的优化问题Fig.3 Optimization under harmonic force excitation

表1 支撑结构和组件的材料参数Table 1 Material properties of supporting and components

材料编号弹性模量E/GPa泊松比μ密度ρ/(kg·m-3)Ⅰ2100.37800

将支撑结构内所有单元的伪密度初值赋为0.4。为了研究初始结构的动态特性，首先对其进行模态和简谐响应分析。由图4可知，在结构的前4阶模态中，只有第4阶模态沿载荷方向振动，对目标自由度的位移响应幅值贡献最大，因此第4阶模态频率是初始结构的1阶共振频率。

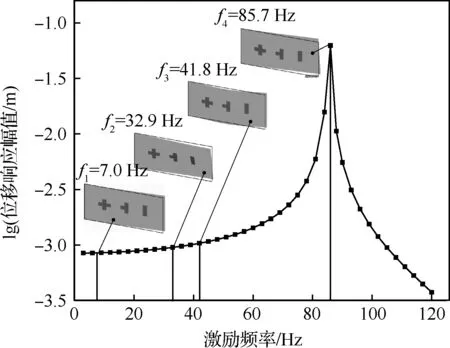
图4 初始结构的位移响应幅值和低阶模态振型Fig.4 Displacement response amplitude and low order mode shapes of initial structure

给定简谐力的激励频率ωp=70 Hz，低于初始结构的1阶共振频率。作为比较，假设组件固定在初始位置，仅对支撑结构进行拓扑优化，优化过程和最终优化构型如图5所示。结果显示，目标自由度的位移响应幅值由2.05 mm减小为0.055 4 mm，且支撑结构和组件共同起到降低结构振动响应的作用。

在组件可以移动的情况下，对支撑结构和组件进行整体优化，优化过程和最终优化构型如图6 所示。结果显示，目标自由度的位移响应幅值由2.05 mm减小为0.052 4 mm。在优化过程中，组件首先移动到合适的位置，然后在支撑结构上逐渐形成一个包含组件的清晰传力路径。由于组件可以自由移动，因此更能获得最优的结构构型。

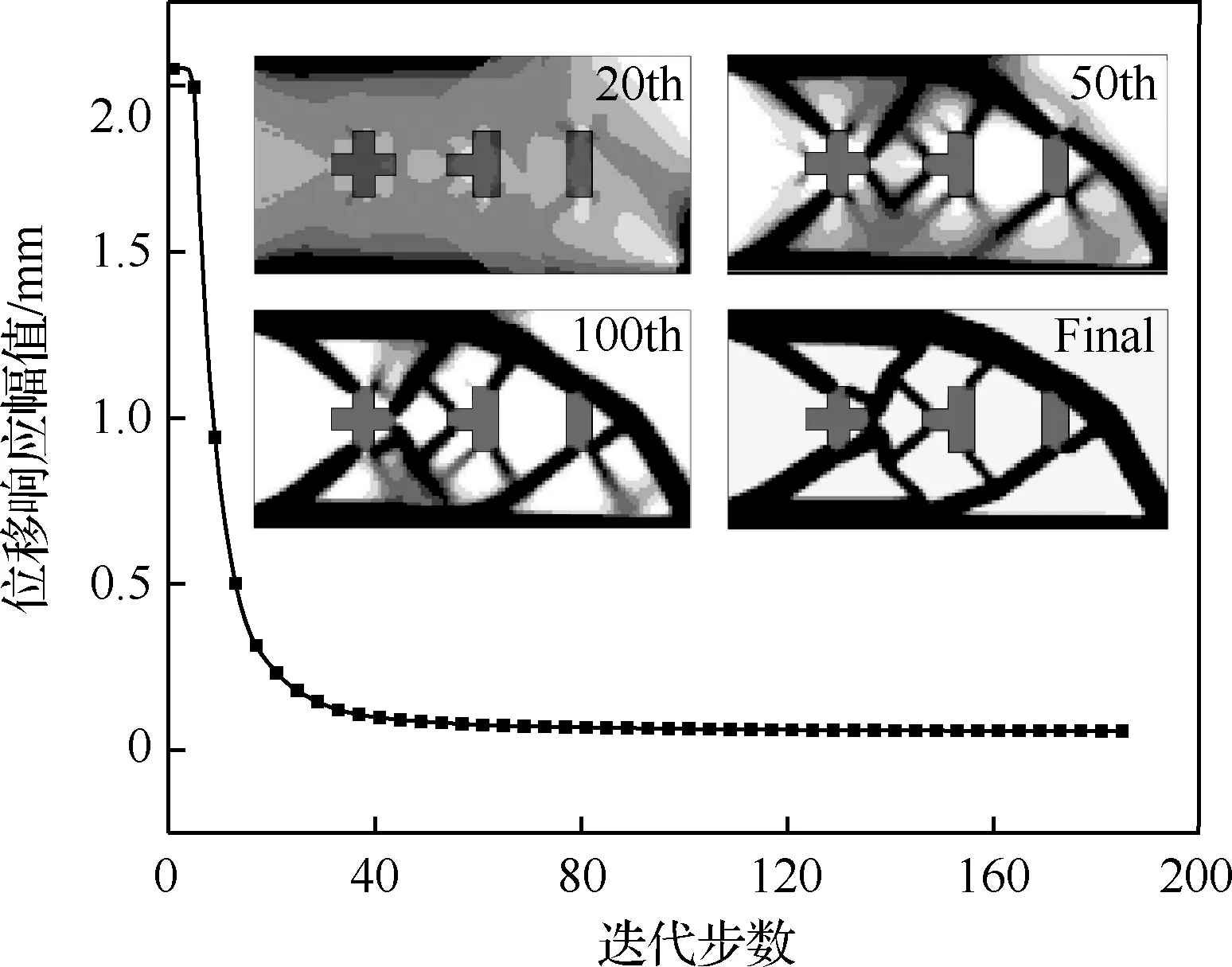
图5 组件固定下的收敛过程Fig.5 Convergence history with fixed components

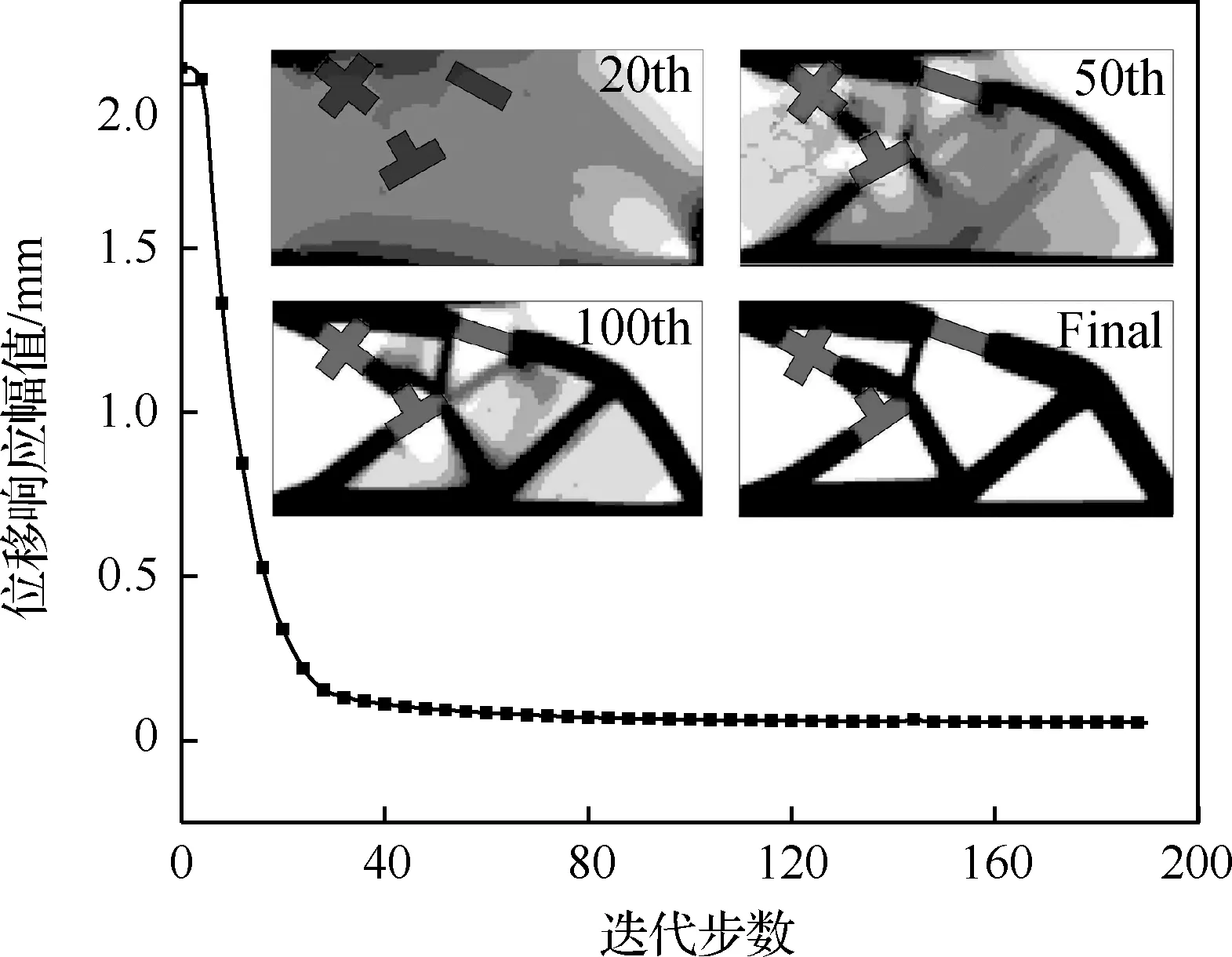
图6 组件移动下的收敛过程Fig.6 Convergence history with moveable components

当简谐力的激励频率ωp=100 Hz，高于结构的1阶共振频率时。经过优化，目标自由度的位移响应幅值由1.41 mm减小为0.004 29 mm。但在最终的优化构型中存在大量中间伪密度单元，结构的固定端和加载点处非常薄弱，使得结构的静力学性能很差(如图7所示),并且，这种优化构型由于没有清晰的材料分布，因此在结构设计中也不具有参考性。

为了深入理解外部激励频率对优化结果的影响，分别对初始结构和前面3个优化后的结构进行简谐响应分析，结果如图8所示。在简谐激励下的优化问题中，一个重要的目标就是使结构的共振频率尽可能远离激励频率。因此，当激励频率低于初始结构共振频率时，只有通过逐步提高结构共振频率才能够避免产生共振。相反，当激励频率高于初始结构共振频率时，在优化过程中，结构的共振频率值会逐渐降低。

由图8可知，当激励频率为70 Hz时，2种优化后结构的共振频率分别由85.7 Hz提高到317.3 Hz和328.8 Hz。但当激励频率为100 Hz时，优化后结构的共振频率反而降低为68.2 Hz。

图7 激励频率ωp=100 Hz时的优化构型Fig.7 Optimized configuration with given excitation frequency ωp=100 Hz

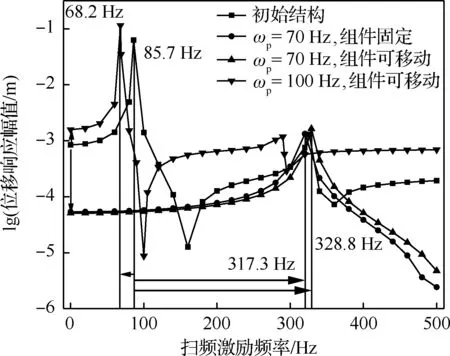
图8 频点激励下初始和3种优化结构的位移响应幅值 Fig.8 Displacement response amplitudes of initial and three optimized structures under certain frequency excitation

针对高于共振频率下简谐激励存在的问题，Olhoff和Du[31]曾提出一种施加静柔顺度约束的方法。最近Olhoff和Du[32]又提出一种广义增量频率法用于解决无阻尼连续结构在简谐力激励下的拓扑优化问题。

3.1.2 频段简谐力激励

在实际问题中，结构通常受到的简谐载荷频率是在[ωA,ωB]范围内。针对这种载荷下的结构优化问题，是以该频段内位移响应幅值的积分最小为目标，如式(50)所示，具体详见文献[20]。

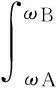
(50)

在图3带组件的悬臂梁结构上分别施加频段为[0,100]、[0,200]和[0,400] Hz的简谐力激励，并允许组件在支撑结构上移动。3种不同频段下优化后的结构构型如图9所示，可以看出，3种优化构型中，组件都能移动到合适位置，并参与降低结构的振动响应。图10表示目标函数的迭代过程，可以看出，优化过程中目标函数值均逐渐降低，并趋于收敛。

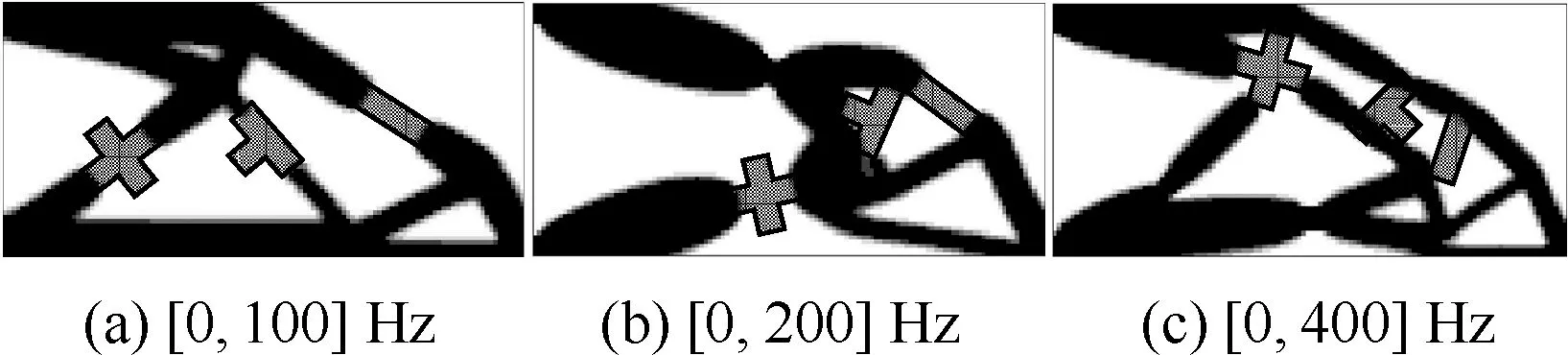
图9 3种不同频段激励下的优化构型Fig.9 Optimized configurations at three different multi-frequency excitation

图10 频段激励下目标函数迭代过程Fig.10 Iteration history of objective function under multi-frequency excitation

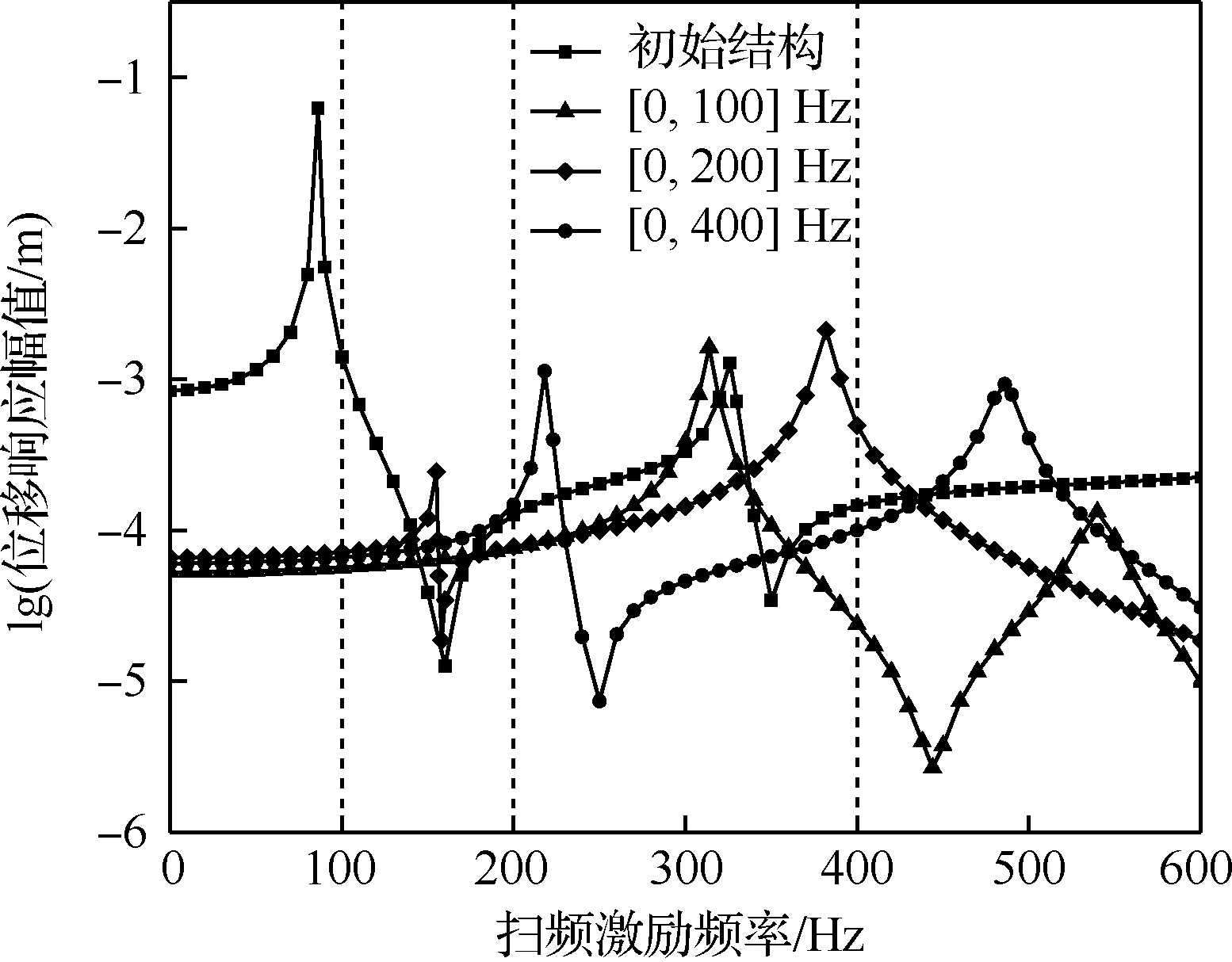
图11 频段激励下初始和3种优化结构的位移响应幅值Fig.11 Displacement response amplitudes of initial and three optimized structures under multi-frequency excitation

同样，对初始结构和3种优化后的结构分别进行简谐响应分析，结果如图11所示。相比于初始结构，3种优化后的结构在低频处的位移响应幅值都有所降低。另外，当频段范围较小时，例如本例中的[0,100]和[0,200] Hz，优化后结构的1阶共振频率明显提高，甚至超出了相应激励频段上限值。但是结构1阶共振频率的提高也是有限的，当频段范围较大时，优化将很难使其超出激励频段的上限值。

3.2 锥形圆柱舱结构系统

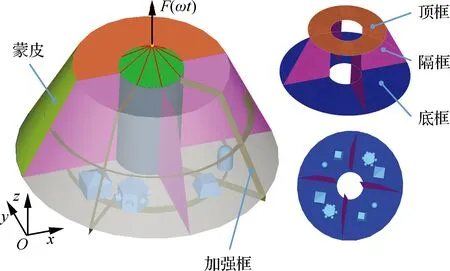
图12 锥形圆柱舱结构系统Fig.12 Conic cylindrical cabin structure system

锥形圆柱舱结构系统如图12所示。结构通过底框处均匀分布的8个节点进行固定，简谐力施加在一个等效的集中质量点上，质量点通过刚性单元与主体结构连接，8个组件对称分布在底框上。其中，框架、隔板、蒙皮及加强筋结构的厚度分别为0.01, 0.012, 0.001 5和0.012 m，底框、顶框和隔板作为设计域，具体结构尺寸如图13所示。组件的有限元模型及MPC节点位置如图14所示。所有结构的材料属性赋为表1中的材料Ⅰ。

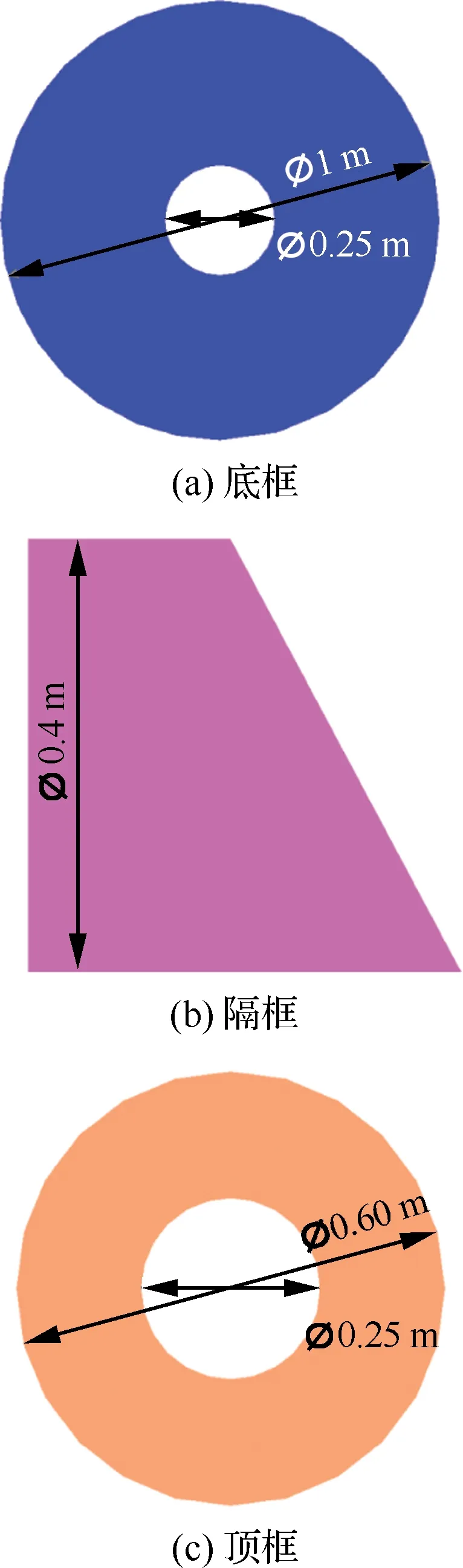
图13 设计域的详细尺寸Fig.13 Detailed sizes of design domain

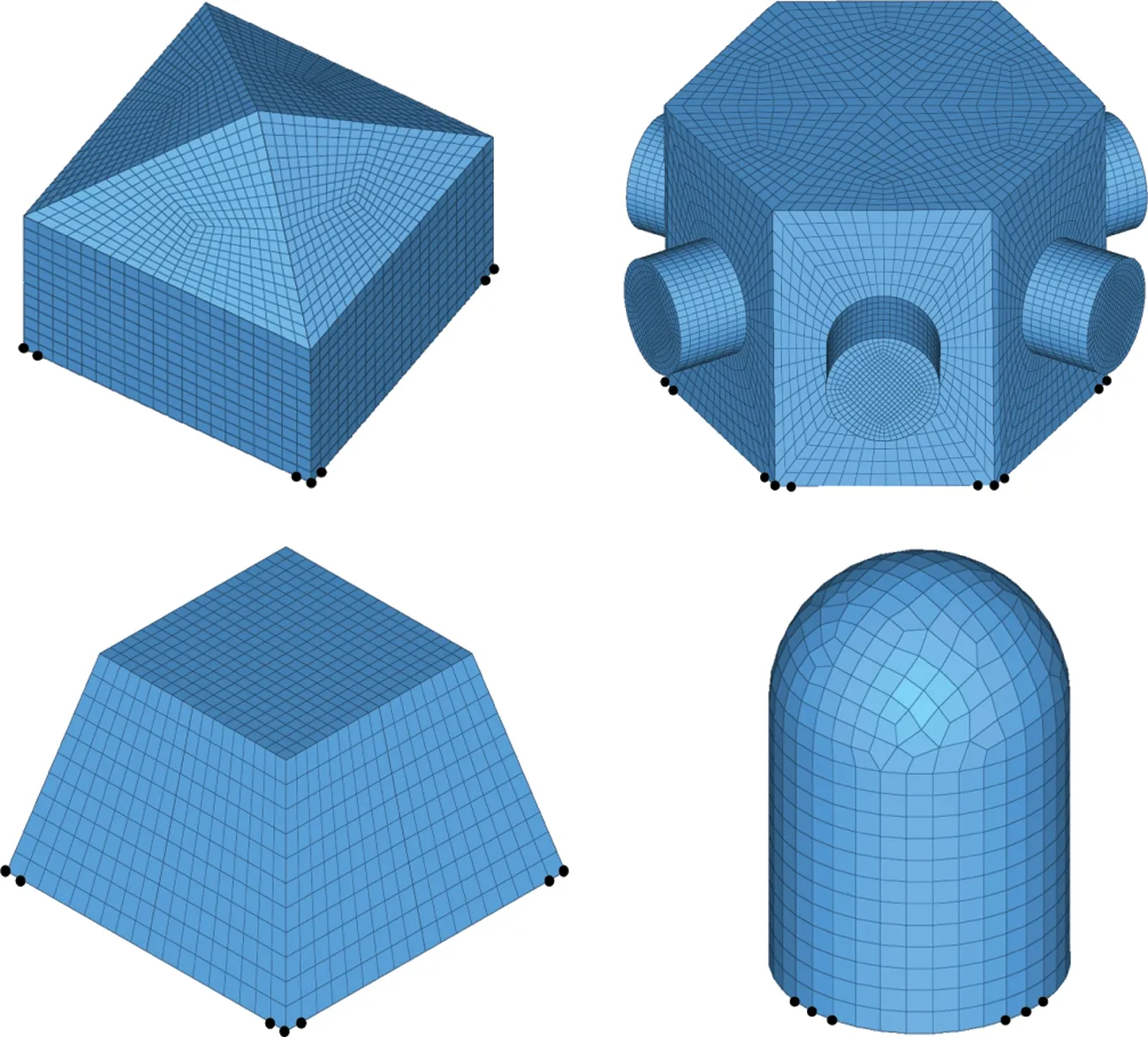
图14 组件的有限元模型和连接节点Fig.14 Finite element models and connection nodes of components

每个组件的位置通过3个参数控制:① 组件局部坐标系与系统整体坐标系原点间的距离R，称为极径；② 极径与整体坐标系中坐标轴的夹角θ，称为极角；③ 组件局部坐标系下的旋转参数γ。其中，R和θ的变化可以通过坐标变换转化为组件在x和y方向坐标的变化，具体如图15所示。

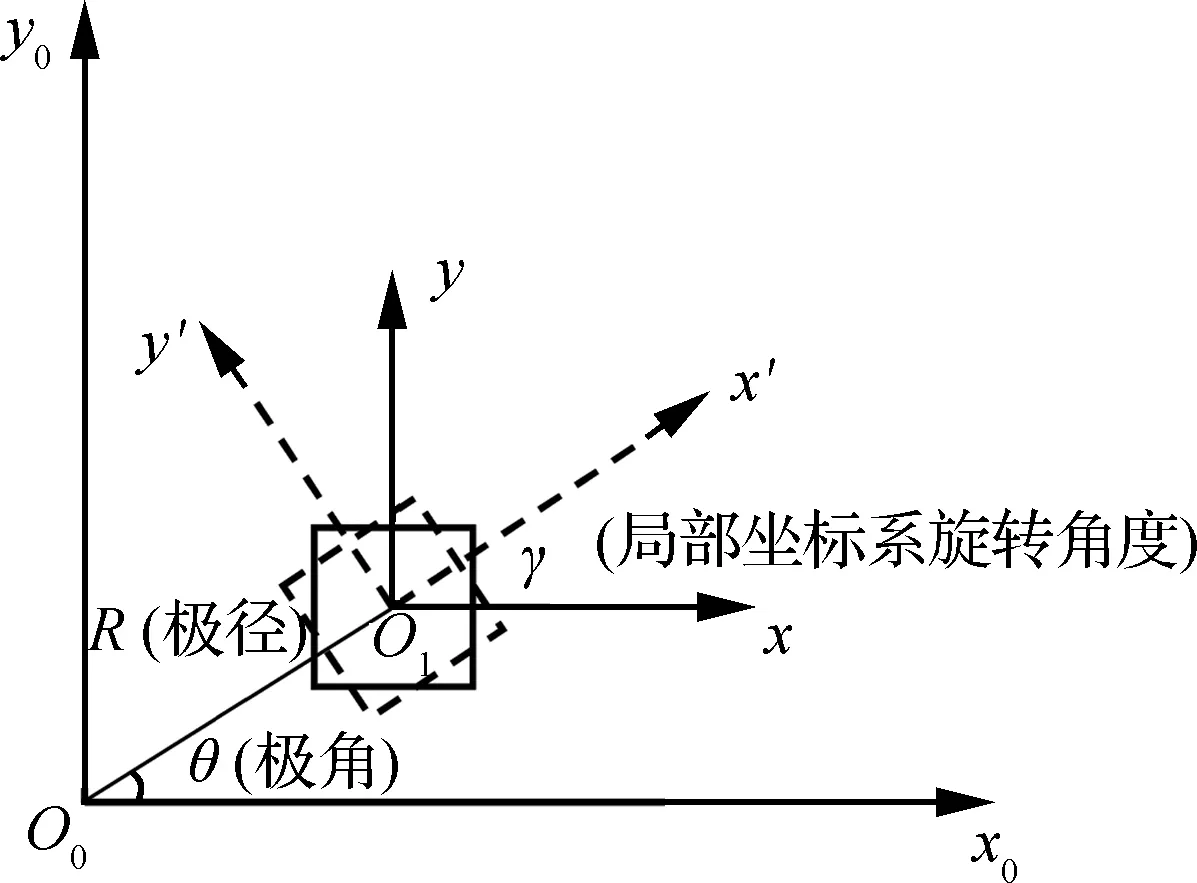
图15 3个控制参数的示意图Fig.15 Schematic of three control parameters

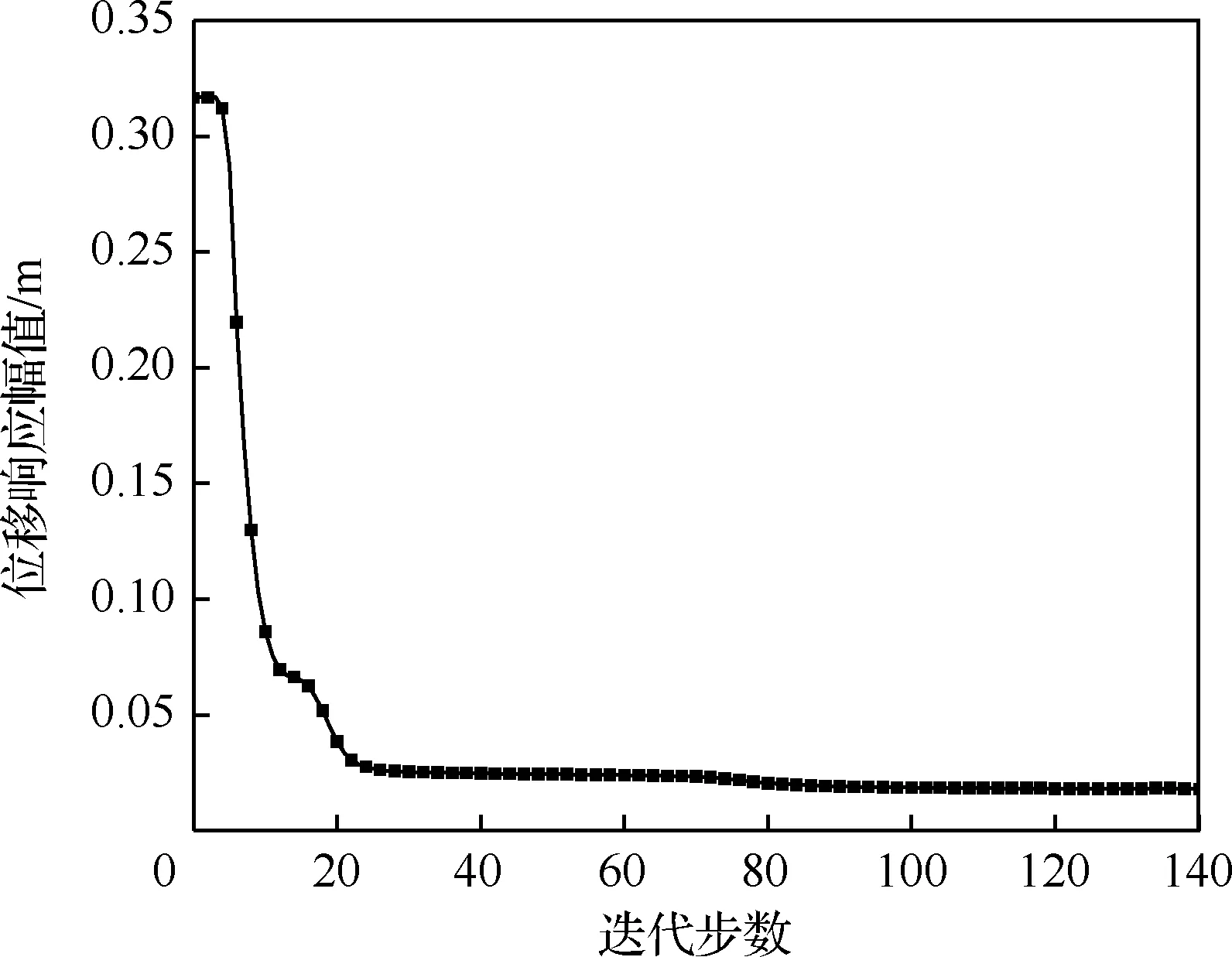
图16 位移响应幅值迭代曲线Fig.16 Iteration curves of displacement response amplitude

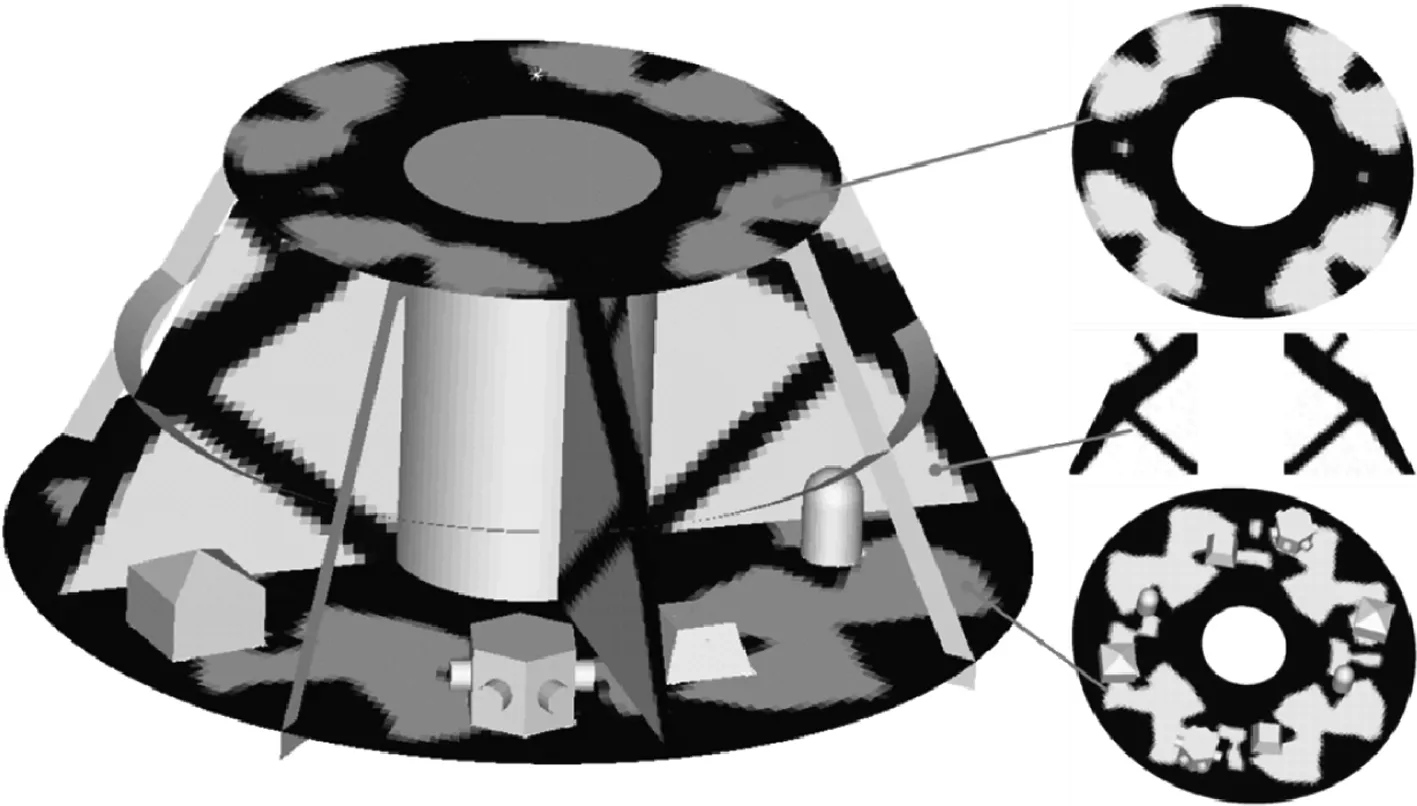
图17 优化构型和组件布局Fig.17 Optimized configurations and layout of components

在加载点处施加频率为80 Hz的简谐力激励(低于初始结构1阶共振频率)，并以加载方向的位移响应幅值最小作为优化目标，设计域中框架和隔板的体积分数分别约束为60%和40%。经过140步迭代，目标函数最终收敛。图16表示目标函数迭代曲线，其中，位移响应幅值由0.317 m下降为0.017 4 m。从图17中可以看出，不仅组件移动到了合适的位置，同时设计域也获得了清晰的拓扑构型。在该优化问题中，隔板作为主要的承力构件，其拓扑构型几乎沿旋转轴对称分布。

对初始结构和优化结构分别进行频率响应分析，获得的位移响应幅值曲线如图18所示。可以看出，不仅结构的1阶共振频率由88.7 Hz提高到179.9 Hz，且位移响应的峰值也有所降低。

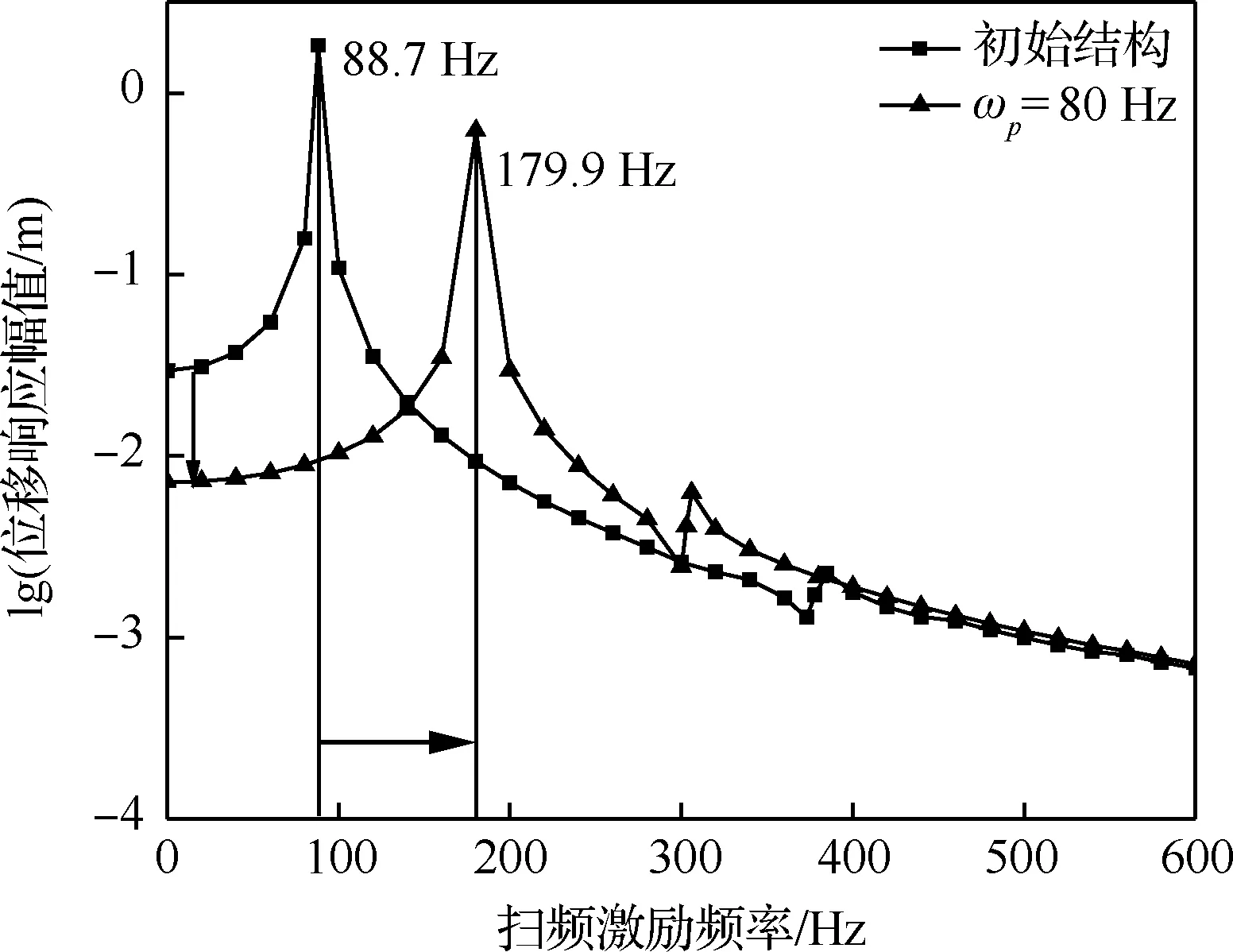
图18 初始结构和优化结构的位移响应幅值Fig.18 Displacement response amplitudes of initial and optimized structures

4 结 论

1) 本文建立了简谐力激励下多组件结构系统整体优化问题的数学模型，并对目标函数关于设计变量的灵敏度进行了推导。

2) 当简谐力激励的频率低于初始结构的1阶共振频率时，经过整体优化可以获得清晰的结构构型，优化后结构不仅1阶共振频率提高，且位移响应峰值也有所下降；当激励频率在某一频率范围内时，通过引入频段优化方法，经过优化同样可以获得清晰的结构构型并提高结构的静力性能。

3) 该整体优化方法不仅针对带组件的简单二维悬臂梁结构有效，同时对于与实际结构接近的锥形圆柱舱结构同样可以优化得到合理的构型。

[1] BENDSØE M P, KIKUCHI N. Generating optimal topologies in structural design using a homogenization method[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224.

[2] HOU J, ZHU J, HE F, et al. Stiffeners layout design of thin-walled structures with constraints on multi-fastener joint loads[J]. Chinese Journal of Aeronautics, 2017,30(4): 1441-1450.

[3] GUO X, CHENG G D. Recent development in structural design and optimization[J]. Acta Mechanica Sinica, 2010, 26(6): 807-823.

[4] ZHU J H, ZHANG W H, XIA L. Topology optimization in aircraft and aerospace structures design[J]. Archives of Computational Methods in Engineering, 2016, 23(4): 595-622.

[5] JIANG T, CHIREHDAST M. A systems approach to structural topology optimization: Designing optimal connections[J]. Journal of Mechanical Design, 1997, 119(1): 40-47.

[6] LI Q, STEVEN G P, XIE Y M. Evolutionary structural optimization for connection topology design of, multi-component systems[J]. Engineering Computations, 2001, 18(3/4): 460-479.

[7] ZHU J H, ZHANG W H, BECKERS P. Integrated layout design of multi-component system[J]. International Journal for Numerical Methods in Engineering, 2009, 78(6): 631-651.

[8] QIAN Z, ANANTHASURESH G K. Optimal embedding of rigid objects in the topology design of structures[J]. Mechanics Based Design of Structures and Machines, 2004, 32(2): 165-193.

[9] KANG Z, WANG Y. Integrated topology optimization with embedded movable holes based on combined description by material density and level sets[J]. Computer Methods in Applied Mechanics & Engineering, 2013, 255: 1-13.

[10] ZHANG W, ZHONG W, GUO X. Explicit layout control in optimal design of structural systems with multiple embedding components[J]. Computer Methods in Applied Mechanics & Engineering, 2015, 290: 290-313.

[11] ZHU J H, GAO H H, ZHANG W H, et al. A multi-point constraints based integrated layout and topology optimization design of multi-component systems[J]. Structural & Multidisciplinary Optimization, 2015, 51(2): 397-407.

[12] PEDERSEN N L. Maximization of eigenvalues using topology optimization[J]. Structural & Multidisciplinary Optimization, 2000, 20(1): 2-11.

[13] DU J, OLHOFF N. Topological design of freely vibrating continuum structures for maximum values of simple and multiple eigenfrequencies and frequency gaps[J]. Structural & Multidisciplinary Optimization, 2007, 34(2): 91-110.

[14] TSAI T D, CHENG C C. Structural design for desired eigenfrequencies and mode shapes using topology optimization[J]. Structural & Multidisciplinary Optimization, 2013, 47(5): 673-686.

[15] MA Z D, KIKUCHI N, CHENG H C. Topological design for vibrating structures[J]. Computer Methods in Applied Mechanics & Engineering, 1995, 121(1-4): 259-280.

[16] JOG C S. Topology design of structures subjected to periodic loading[J]. Journal of Sound & Vibration, 2002, 253(3): 687-709.

[17] SHU L, WANG M Y, FANG Z, et al. Level set based structural topology optimization for minimizing frequency response[J]. Journal of Sound & Vibration, 2011, 330(24): 5820-5834.

[18] YOON G H. Structural topology optimization for frequency response problem using model reduction schemes[J]. Computer Methods in Applied Mechanics & Engineering, 2010, 199(25-28): 1744-1763.

[19] BESSELINK B, TABAK U, LUTOWSKA A, et al. A comparison of model reduction techniques from structural dynamics, numerical mathematics and systems and control[J]. Journal of Sound & Vibration, 2013, 332(19): 4403-4422.

[20] LIU H, ZHANG W H, GAO T. A comparative study of dynamic analysis methods for structural topology optimization under harmonic force excitations[J]. Structural & Multidisciplinary Optimization, 2015, 51(6): 1321-1333.

[21] 刘虎, 朱继宏, 张卫红. 简谐载荷作用下连续体结构位移响应拓扑优化[J]. 机械制造, 2012, 50(7): 27-30.

LIU H, ZHU J H, ZHANG W H. Topological optimization of continuue structures with displacement response under harmonic load[J]. Machinary, 2012, 50(7): 27-30 (in Chinese).

[22] 张卫红, 郭文杰, 朱继宏. 部件级多组件结构系统的整体式拓扑布局优化[J]. 航空学报, 2015, 36(8): 2662-2669.

ZHANG W H, GUO W J, ZHU J H. Integrated layout and topology optimization design of multi-component systems with assembly units[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2662-2669 (in Chinese).

[23] ZHANG Q, ZHANG W H, ZHU J H, et al. Layout optimization of multi-component structures under static loads and random excitations[J]. Engineering Structures, 2012, 43(43): 120-128.

[24] LIU G R, QUEK S S. The finite element method: A practical course[M]. Oxford: Butterworth-Heinemann, 2003: 271-277.

[25] CLOUGH R W, PENZIEN J, GRIFFIN D S. 结构动力学[M]. 陈嘉炜, 译. 台北： 科技图书股份有限公司, 1981: 271-284.

CLOUGH R W, PENZIEN J, GRIFFIN D S. Dynamics of structures[M]. CHEN J W, translated. Taipei: Technology Books Co. Ltd., 1981: 271-284 (in Chinese).

[26] BENDSØE M P, SIGMUND O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69(9): 635-654.

[27] 朱继宏, 张卫红, 邱克鹏. 结构动力学拓扑优化局部模态现象分析[J]. 航空学报, 2006, 27(4): 619-623.

ZHU J H, ZHANG W H, QIU K P. Investigation of localized modes in topology optimization of dynamic structures[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(4): 619-623 (in Chinese).

[28] STOLPE M, SVANBERG K. An alternative interpolation scheme for minimum compliance topology optimization[J]. Structural & Multidisciplinary Optimization, 2001, 22(2): 116-124.

[29] ZHU J H, BECKERS P, ZHANG W H. On the multi-component layout design with inertial force[J]. Journal of Computational & Applied Mathematics, 2010, 234(7): 2222-2230.

[30] BENDSOE M P, SIGMUND O. Topology optimization: Theory, methods, and applications[M]. Berlin: Springer Science & Business Media, 2013: 16-17.

[31] OLHOFF N, DU J. Topological design of continuum structures subjected to forced vibration[C]∥Proceedings of 6th World Congresses of Structural and Multidisciplinary Optimization. Rio de Janeiro: Engopt Orgnization, 2005: 1-8.

[32] OLHOFF N, DU J. Generalized incremental frequency method for topological design of continuum structures for minimum dynamic compliance subject to forced vibration at a prescribed low or high value of the excitation frequency[J]. Structural and Multidisciplinary Optimization, 2016, 5(54): 1113-1141.