正态型有寿件的备件方案确定方法

邵松世，张志华，李华，刘任洋

1.海军工程大学 科研部，武汉 430033 2.海军工程大学 兵器工程系，武汉 430033 3.海军装备研究院，北京 100161

有寿件是规定了预防性维修更换或报废期限及可以预计使用寿命的一类备件[1]，亦称限寿件。使用有寿件能有效地预防故障发生，最大限度的保持装备的战备完好状态。因此，在航空领域，对于故障后可能造成严重后果的飞机部件，有寿件的使用及保障问题事关重大。

对于有寿件保障方案的确定，主要包括备件需求量的确定以及更换周期的确定。目前对于有寿件备件需求的研究并不多，计算备件需求量的方法主要是基于实际平均消耗数量再乘以一个大于1的加权系数的统计方法，如GJB4355-2002[1]。该方法仅是经验上的近似方法，无法对实际保障效果进行有效评估。文献[2]提出了一种基于指数等效的有寿件备件满足率评估模型，但其仅针对指数型有寿件，且存在不小的误差。更换周期是有寿件的一项重要参数，如何科学、合理地确定部件更换周期，是使用有寿件的关键问题。国外在这方面开展的研究较多。文献[3]研究了免维修费用下可修产品定期更换策略的优化问题。文献[4]研究了单部件系统在执行不间断任务时的更换策略问题。但包括以上文献在内的绝大部分研究均针对商业需求[5-8]，通过使费用最低化，寻找最佳更换策略，而对于飞机部件，经济效益显然不是最重要的，部件的未到寿故障可能直接导致灾难性后果，因此安全效益是航空领域需要考虑的主要因素。此外，现有研究基本仅限于讨论定期更换的策略问题，而少有将定期更换与备件数量结合起来进行综合考虑。

本文针对上述问题，以寿命服从正态分布的部件为例，采用寿命等效思想，提出了一种确定有寿件备件需求量和更换周期的方法，能够为有寿件保障方案的制定提供决策支持。

1 正态有寿件需求量的确定方法

1.1 有寿件的寿命等效原理

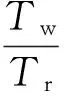
通过分析：有寿件的到寿更换意味着其工作寿命在某个时刻戛然而止。这与正态分布的“集中”故障(99.73%的正态变量落在(μ-3σ,μ+3σ)范围内，μ为正态分布的均值，σ为标准差)在现象上有相似之处，可以尝试以正态分布来近似描述有寿件的工作寿命分布，再利用正态型备件需求量计算方法计算有寿件的备件需求量。

对于正态有寿件而言，通常其更换周期应定于部件寿命均值μ以内，否则在更换周期内发生故障的概率将很大。图1所示为参数(μ,σ)=(600,200)的正态有寿件在更换周期分别为400、500 和600 h下与所等效正态单元的可靠度曲线对比,t为备件工作时间，从图中可以看出两者具有较好的相似性，这在一定程度上验证了用正态分布来近似描述有寿件工作寿命分布的可行性。

1.2 备件需求量确定流程

步骤1正态等效。即将有寿件的工作寿命分布等效为正态分布，采用贝叶斯理论[9]，具体步骤为

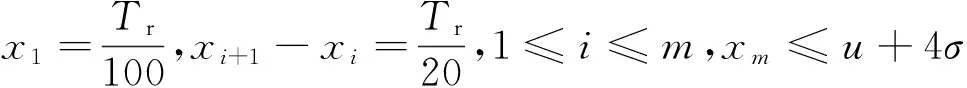
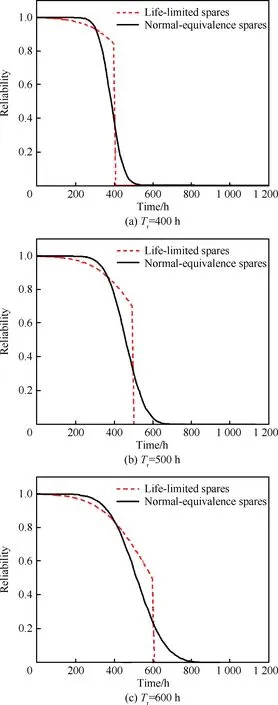
图1 不同更换周期下有寿件与等效正态 单元的可靠度对比 Fig.1 Comparison of reliability of life-limited item and equivalent normal distribution ones at different replacement cycle

4) 在数组{x1,x2,…,xm}中找到最接近Tr的数xp，即xp≤Tr且xp+1>Tr。

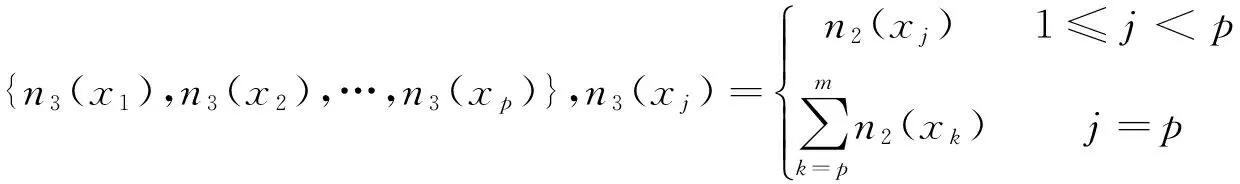
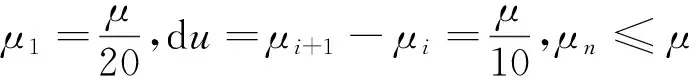
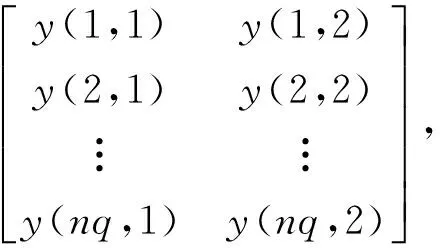
令k=0

fori=1:n

forj=1:q

k=k+1;y(k,1)=μi;y(k,2)=σj;

end

end

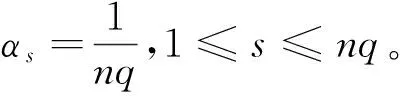
9) 对权重系数组{α1,α2,…,αnq}进行循环更新，具体为

A) 令i1=1

B) 令x2=xi1,i2=1

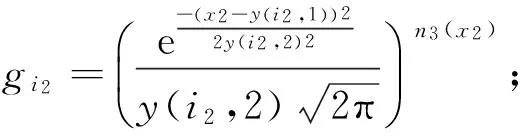
D) 更新i2，令i2=i2+1。如果i2≤nq,则执行C)，否则执行E)

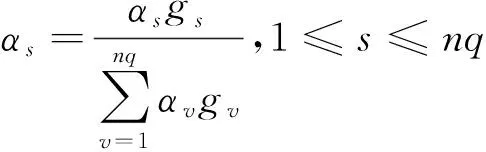
F) 更新i1，令i1=i1+1。如果i1≤m,则执行B)，否则执行10)。

(1)

(2)

步骤2计算备件保障概率P或使用可用度A:

(3)

(4)

式中：S为备件数量。

步骤3根据给定的备件保障概率指标P0或使用可用度指标A0,迭代求解备件需求量S。

2 正态有寿件更换周期的确定方法

在确定有寿件的更换周期时，通常应考虑以下2个问题：

1) 有寿件在更换周期内能可靠工作的程度能否满足指标要求？

2) 在满足战备完好性或备件保障概率等指标要求下，能否尽可能少地配置备件？

对于问题1)，有寿件工作到期限而更换是喜闻乐见的，因故障而更换则是不希望的、后果可能是很严重的。显然，当更换周期越短，期限内发生故障的可能性就越低。问题1)从更换周期内能否不发生故障的角度描述了选定某更换周期的安全收益。对于问题2)，当更换周期越短时，直觉上会觉得需要更多的备件。问题2)从备件采购费用的角度描述了选定某更换周期的经济成本。

为了回答问题1)，提出有寿件的到寿更换概率这一概念，将其定义为有寿件在更换周期Tr内可靠工作、不发生故障的概率。对于寿命服从正态分布N(μ,σ2)的单元而言，其到寿更换概率为

(5)

对于问题2)，其本质是一个保障效果评估问题，即：当已知单元的寿命分布规律、更换周期、备件数量和保障任务周期时，能否定量计算备件保障概率或使用可用度等保障效果。该问题已在第1节中得到解决。

通过以上对更换周期安全收益和经济成本的量化考量和综合权衡，就可以确定合理的更换周期。

3 算例验证与分析

为了验证上述方法的有效性，建立如下有寿件的备件保障仿真模型，开展仿真验证。该仿真模型模拟了一次保障任务过程。仿真模型的具体流程如下：

1) 模拟寿命

产生1+S个随机数ti,ti服从正态分布N(μ,σ2)。

2) 模拟工作寿命

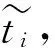
(6)

3) 输出模拟结果

模拟结果有2项：保障任务成功标志Flag和保障期内正常到寿更换的比例simR。simR定义为：在保障期内，到寿更换的次数与总更换次数之间的比例。simT为仿真模型中有寿件的实际工作时间。

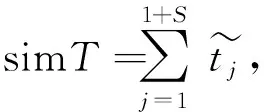
(7)

在多次运行该仿真模型后，对Flag进行统计，其均值simP既为保障任务成功率的仿真结果，也是备件保障概率的仿真结果[10]。

算例1假设寿命服从参数(μ,σ)=(600,130)的正态分布有寿件，保障周期Tw=2 000 h,更换周期Tr的取值范围为200～500 h，规定整个任务期的备件保障概率指标值为0.85，在更换周期内不发生故障的概率不低于0.85，现要求制定该正态有寿件的备件方案，包括确定备件需求数量和更换周期。分别利用本文正态等效法与仿真方法对不同更换周期下的备件需求量和到寿更换概率进行计算，结果如表1所示。从表中可以看出：正态等效法的精度较高，绝对误差均在2%以内，说明了方法的有效性。当更换周期Tr分别为400 h和450 h时，备件需求量均为5，此时两者的备件保障概率均极为接近1，而Tr=400 h的到寿更换概率为0.938，明显高于Tr=450 h时的0.876，因此400 h的更换周期无疑是更好的选择。

算例2将算例1中的正态分布寿命参数改为(μ,σ)=(600,230),其他参数不变，所得结果如表2所示。此算例主要验证和讨论正态有寿件寿命根方差σ相对其均值μ较大的情况。从表2的结果同样可以看出正态等效法的有效性。通过分析，300 h和350 h是较佳的更换周期候选方案，此时两者的备件需求量均为7，虽然后者比前者的到寿更换概率降低了4.76%，但备件保障概率大幅度提高了15.36%。因此，Tr=350 h可能是更好的选择。

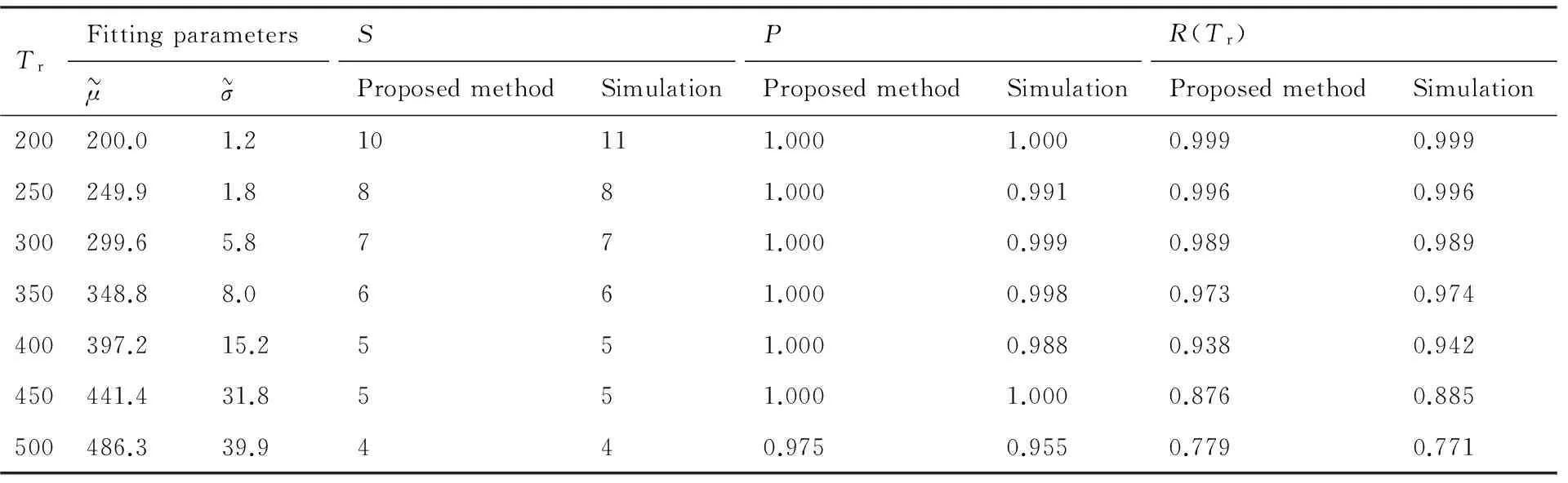
表1 算例1中本文方法与仿真方法的结果对比Table 1 Comparison of results of our method and simulation in Example 1

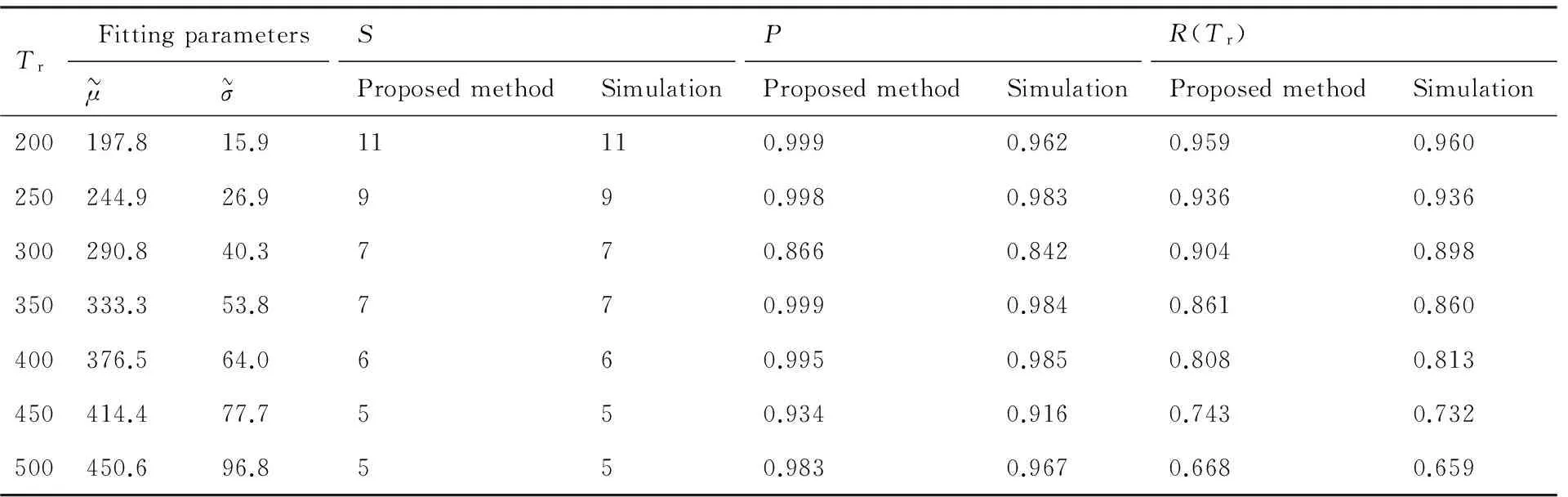
表2 算例2中本文方法与仿真方法的结果对比Table 2 Comparison of results of our method and simulation in Example 2

算例1和算例2分别代表了部件寿命的根方差较小和较大这两种情况。大量仿真验证结果表明：利用本文方法计算得到的结果(备件需求量、备件保障概率和到寿更换概率)与仿真结果都极为接近。本文方法能使备件保障人员在准确了解各种更换周期的备件采购成本与安全收益的情况下，辅助确定有寿件的备件需求量和更换周期。

4 结 论

1) 提出了基于正态等效的有寿件备件需求量计算方法，解决了有寿件备件需求预测难、精度不高的问题。

2) 通过引入到寿更换概率作为度量安全收益的指标，提出了有寿件最佳更换周期的确定方法。

[1] 中国人民解放军总装备部. 备件供应规划要求: GJB4355-2002[S]. 北京：国防工业出版社，2003: 21-22.

The PLA General Armament Department. Spares provisioning requirements: GJB4355-2002[S]. Beijing:National Defense Industry Press,2003: 21-22 (in Chinese).

[2] 金正, 张志华, 应新雅. 舰船装备限寿备件满足率评估模型[J]. 指挥控制与仿真,2015,37(4): 130-133.

JIN Z, ZHANG Z H, YING X Y. Evaluation and model of ship life limited items sufficiency[J]. Command Control & Simulation, 2015,37(4): 130-133(in Chinese).

[3] RUEY H Y, CHEN M Y, LI C Y. Optimal periodic replacement policy for repairable products under free-repair warranty[J]. European Journal of Operational Research, 2007, 176(3): 1678-1686.

[4] LI Y, MA X B, ZHAI Q Q, et al. A delay time model for a mission-based system subject to periodic and random inspection and postponed replacement[J]. Reliability Engineering and System Safety, 2016, 150: 96-104.

[5] GOLMAKANI H, MOAKEDI H. Periodic inspection optimization model for a two-component repairable system with failure interaction[J]. Quality and Reliability Engineering International, 2012, 63(3): 540-549.

[6] NAKAGAWA T, MIZUTANI S. A summary of maintenance policies for a finite interval[J]. Reliability Engineering and System Safety, 2009, 94: 89-96.

[7] SCARF P, CAVALCANTE C. Modeling quality in replacement and inspection maintenance[J]. International Journal of Production Economics, 2012,135(1): 372-381.

[8] TAGHIPOUR S, BANJEVIC D, JARDINE A. Periodic inspection optimization model for a complex repairable system[J]. Reliability Engineering and System Safety, 2010, 95: 944-952.

[9] 韦来生, 张伟平. 贝叶斯分析[M]. 合肥：中国科学技术大学出版社, 2013: 99-103.

WEI L S, ZHANG W P. Bayesian analysis[M]. Hefei: University of Science & Technology China Press, 2013: 99-103(in Chinese).

[10] 李华, 邵松世, 阮旻智,等.备件保障的工程实践[M].北京: 科学出版社, 2016: 5-11.

LI H, SHAO S S, RUAN M Z, et al. The engineering practice of spare parts support[M]. Beijing: Science Press, 2016: 5-11(in Chinese).