多机构比对融合的分布式InSAR编队星间基线确定

易彬，秦显平，谷德峰,*，鞠冰

1.国防科技大学 文理学院，长沙 410073 2.西安测绘研究所, 西安 710054

低轨卫星编队被广泛应用于多种测量任务，如地球重力场测量、合成孔径雷达(Synthetic Aperture Radar, SAR) 成像和气象侦察等领域[1-2]，如重力反演与气候实验(Gravity Recovery and Climate Experiment，GRACE)[3]、TerraSAR-X add-on for Digital Elevation Measurement (TanDEM-X)[4]、Constellation Observing System for Meteorology, Ionosphere, and Climate (COSMIC)[5]、Prototype Research Instruments and Space Mission technology Advancement (PRISMA)[6]、实践9号编队任务(Shi Jian-9 formation flight mission，SJ-9)[7]等。分布式干涉合成孔径雷达(Interferometric Synthetic Aperture Radar, InSAR)是近年来提出的一种新概念天基雷达系统，通过将SAR天线固定在编队飞行的卫星上，把低轨卫星的编队飞行技术和InSAR技术相结合，极大地拓展了SAR卫星系统的总体性能，可完成地面目标三维定位、地表形变监测等任务，有着广泛的应用前景[8]。星间基线高精度确定是其任务实现的前提和关键，为了获得高质量的地理信息产品，分布式InSAR对星间基线测量精度的要求极其苛刻。以TanDEM-X为例，该任务是由德国宇航中心(DLR)提出的分布式InSAR系统，在TSX卫星基础上，再发射一颗基本相同的TDX卫星组成双星HELIX(螺旋式)编队，两颗星上均搭载主动式X波段相控阵SAR天线以及跟踪、掩星和测距(Tracking, Occultation and Ranging，TOR)装置。TOR装置由与GRACE卫星类型相同的星载双频GPS(Global Positioning System)接收机和激光后向反射镜组成，用于获取干涉处理所需要的绝对轨道和高精度星间基线测量信息[9]。TanDEM-X用于地面高程测量时，数字高程模型产品精度指标满足高分辨率地面信息第三等级精度要求，但前提是星间基线的确定精度为1～2 mm[9-10]。

TanDEM-X任务与GRACE任务的星间测量设备均采用TOR。GRACE是由德国DLR和美国航空航天局(National Aeronautics and Space Administration，NASA)合作开发的重力场测量卫星系统，两颗卫星运行轨道的倾角为90°，轨道高度大约为500 km，星间距离大约为220 km。GRACE 系统的有效载荷主要有KBR(K/Ka-Band Ranging)系统、TOR、加速度计等[8]。其中KBR可提供精度为1 μm/s 的星间距离变化量，主要用于反演地球重力场的变化，还能作为外部手段校核星间基线的测量精度[11]。TanDEM-X任务自身没有安装KBR系统，目前文献上关于其星间基线测量精度的证明大多是通过GRACE系统间接给出的。

星载双频GPS具有全天候、连续性、高精度、低成本、时空覆盖广等优点，通过在编队飞行的低轨卫星上安装双频GPS接收机，采用载波相位差分GPS(Carrier-phase Differential GPS，CDGPS)、双差整周模糊度固定和简化动力学技术，可以提供毫米级的编队卫星相对定位精度[11]。2005年，Kroes等利用基于简化动力学的序贯广义卡尔曼滤波 (Extended Kalman Filter，EKF)方法确定GRACE卫星相对位置，KBR检核基线精度达到1 mm，模糊度固定成功率达到83%[12]。2007年，Jäggi等提出批处理最小二乘方法来确定GRACE卫星相对位置，KBR检核基线精度为0.88 mm，模糊度固定成功率为89.8%[13]。受大气阻力、非球形引力等摄动力影响，分布式InSAR编队几何构型会随时间推移而逐渐被破坏，因此需要通过频繁的轨道机动控制来维持特定的编队构型[14]，2015年，Ju等通过对机动力合理建模以及机动附近数值积分方法的改进，消除机动对GRACE精密轨道和基线确定的影响，机动条件下的KBR检核基线精度为0.7 mm，模糊度固定成功率为87%[15]。随着基线确定精度不断提高，基线确定的可靠性受到越来越多的关注。2016年，Allende-Alba和Montenbruck研究了分布式低轨编队基线确定的稳健方法，指出基线确定不可靠的主要原因来自卫星的高速运动，导致接收机载波相位连续跟踪弧段变短，模糊度正确解算难度增加，为此优化了整周模糊度固定策略，将GRACE基线的KBR检核精度由0.95 mm提高到0.72 mm，同时基线天解精度优于2.5 mm的天数也由95.2%提高到99.4%[16]。

一方面，受GPS连续跟踪弧段共视卫星个数、模糊度固定成功率以及频繁轨道机动等因素的影响，分布式InSAR高精度基线确定仍存在一定的不可靠风险；另一方面，大多分布式InSAR采用相互绕飞的编队模式，与采用同轨道前后跟飞模式的GRACE双星编队不同，难以通过窄波束的KBR手段实现基线精度校核。分布式InSAR任务每轨的成像时间较短，只有几分钟，并不要求所有时间的基线解都一定是高精度的，但要避免低精度时间段内的基线解参与InSAR处理，污染最终地理定位产品的精度。在缺少外部KBR检核手段条件下，如何获得基线确定的精度信息成为关键。单个机构难以提供可靠的基线确定精度信息，本文通过多机构产品互比来识别基线精度较差的时间段，降低单个机构基线确定中的不可靠风险，并通过多机构产品融合进一步提高基线精度。首先，举例分析了影响基线高精度确定的不可靠因素；其次，比较了不同机构NDT和CHS基线软件的处理方法差异；然后，互比对分析了不同机构基线产品的一致性；最后，进行基线融合，得到更高精度且可靠的基线融合产品。为方便研究过程中对不同机构以及融合后的基线产品进行KBR精度检核，本文在研究中仍选用GRACE编队数据，尽管如此，所得到的研究结果可应用到其他分布式InSAR编队星间基线高精度确定。

1 星间基线确定的不可靠性因素分析

星间基线确定采用CDGPS技术，利用差分消除或削弱公共误差(如卫星钟差，GPS星历误差)的影响，双差载波相位观测方程为

(1)

虽然利用CDGPS技术可获得毫米级的相对定位精度，但是受星载GPS接收机连续跟踪弧段较短、个别弧段的共视GPS卫星个数偏少或模糊度固定成功率偏低、频繁轨道机动等不利因素的影响，分布式InSAR高精度基线确定仍存在一定的不可靠风险。

低轨卫星的高速运动会导致星载接收机对GPS卫星的连续跟踪时间相对于地面观测条件明显变短，单次连续跟踪时间不足一个小时。以GRACE卫星为例，卫星轨道周期约为90 min，飞行速度约为7.6 km/s，卫星绕地球飞行过程会频繁进出GPS卫星发射信号的视场范围，此时接收机对某颗GPS卫星的单次连续跟踪时间长短与二者相互几何位置关系有关，最长时间约为47 min，平均仅为23 min左右。星载GPS接收机连续跟踪弧段较短，导致在编队基线确定CDGPS双差相位模糊度解算时会面临参考GPS卫星i频繁更换的问题，给模糊度固定带来一定的困难。一种解决参考GPS卫星更换问题的主要策略是采用模糊度分段解算，通常选择连续跟踪时间较长的GPS卫星作为参考卫星，保证在每个分段区间内共视GPS卫星不发生更换。在地面条件下，模糊度分段解算区间的时间长度往往可以达到数小时，但在星载条件下，由于GPS卫星频繁更换，该处理方法模糊度分段解算区间的时间长度较小。

图1为2007年05月09日约2个轨道周期内GRACE A和GRACE B的共视GPS卫星跟踪和模糊度分段区间情况，虚线代表分段区间，模糊度分段解算区间的平均长度仅为30 min左右。

GPS双差相位模糊度具有整数特性，如果模糊度被准确固定，则双差观测模型中的模糊度参数会被消除，此时相位观测数据会被转换成高精度相对距离，可实现高精度的相对定位，因此，每个分段区间的双差模糊度能否被高成功率的固定是实现高精度星间基线确定的关键。模糊度求解可转换为式(2)所示的最小化问题:

(2)

图1 2007-05-09 GRACE A和GRACE B的 共视GPS可用卫星
Fig.1 Visible GPS satellites from GRACE A and B on 9 May 2007

图2 2007-05-09模糊度数与基线KBR校准残差
Fig.2 Number of ambiguities and KBR residuals on 9 May 2007

特别地，如果某个分段区间的模糊度无法固定或固定个数偏少，则会影响该时间段附近的基线确定精度。图2为2007年05月09日GRACE基线确定的模糊度固定个数和KBR检准残差情况，可见24小时观测数据被大致分成了44个模糊度分段解算区间，双差模糊度的总数321，成功固定283，固定成功率88.16%，在大部分时间里，KBR检核残差均在3 mm以内，但在3：20至4:53 时间段附近，KBR检核残差明显超差，量级达到了14 mm左右，主要原因是这段时间内模糊度成功固定的个数明显偏少，严重影响了其附近的基线产品精度。

如果个别弧段共视GPS卫星个数偏少，会直接导致相应时间段的模糊度固定个数偏少。共视GPS卫星个数与导航星座几何分布、低轨卫星轨道高度和接收机多通道连续跟踪能力相关，其中接收机多通道连续跟踪能力的偶然下降是导致个别弧段共视GPS卫星个数偏少的主要原因。以GRACE卫星为例，统计了2007年1月份至4月份GRACE A和GRACE B大约一百万个历元时刻的数据，图3给出了共视GPS卫星个数分布情况，图中数字代表相应的共视卫星数的历元数，共视GPS卫星个数最多10颗，平均6.37颗，大多时刻在5～8颗左右，其中小于等于3的情况仍占1.6%，不可忽略。而且，这种由于接收机自身性能下降所导致的共视GPS卫星个数偏少现象的出现大多是偶然的，难以避免。这种由于数据质量所导致的模糊度固定个数偶然偏少现象很难通过改进模糊度固定方法来克服，成为影响分布式InSAR高精度基线确定的主要不可靠因素。

再者，与地面运动目标不同，卫星轨道运动具有较强的动力学规律，高精度星间基线确定可利用轨道力学模型约束，采用简化动力学技术来平滑观测误差。卫星轨道力学加速度表达式为

图3 GRACE A和GRACE B的共视GPS卫星数
Fig.3 Visible GPS satellites from GRACE A and B

aRL+aRTN+aMAN

(3)

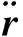
机动力为非保守力，它的存在会破坏原有的轨道力学规律，在星间基线确定中需要被精确的校准和补偿[15]，频繁的机动会增加基线确定的不可靠性。分布式InSAR卫星在编队飞行过程中需要定期通过机动力控制来保持特定的编队构型。在TanDEM-X任务中，TSX卫星每周都要执行一次机动使其在预定的轨道上飞行，为了维持双星HELIX编队，TDX卫星每天需执行两次机动[15]。Jäggi在2012年针对TanDEM-X, 分别在包含机动时段和去掉机动时段两种情况下，统计了AIUB (Astronomical Institute of the University of Bern)和DLR的基线产品互比对精度，机动的加入使得R、T、N方向基线产品互比对标准差分别由机动前的0.5、0.8、1.0 mm增大到机动后的0.8、1.2、1.1 mm[17]，可见，频繁的轨道机动也可能会部分降低基线确定精度，增加基线确定的不可靠性。

受模糊度固定个数偶然偏少、频繁机动等因素的影响，单个机构的分布式InSAR基线产品难以保证在所有时间段内的都是高精度的。加上缺少外部KBR检核手段，单个机构难以提供可靠的基线精度信息。如果低精度时间段内的基线产品参与InSAR处理，将严重污染最终地理定位产品的精度。此时如何获得分布式InSAR基线确定精度和可靠性信息成为关心的问题。为此，本文研究通过多机构产品互比来识别基线精度较差的时间段，降低单个机构基线确定中的不可靠风险，并通过多机构产品融合进一步提高基线精度。

2 星间基线确定方法

星间基线确定通过星上高精度GPS相位观测和地面事后精密轨道确定技术来实现，包括GPS数据预处理、单星绝对轨道确定、双星相对轨道确定、简化轨道动力学模型、双差模糊度固定、天线相位中心变化估计等。以双星编队为例，卫星A的轨道可通过单星GPS绝对定轨技术来实现，卫星B的轨道则主要通过双星GNSS相对定轨来完成。二者的主要区别是双星GPS相对定轨中采用CDGPS技术，对两颗近距离编队飞行卫星的GPS载波相位测量数据进行差分，可以减弱或消除各种公共误差影响，提高观测精度，同时双星GPS相对定轨中采用了双差模糊度固定技术，模型的约束更强，参数估计精度更高。此外，卫星轨道运动较强的动力学规律，可以精确建模，然而地面的运动往往是不可预测的，这是星载条件的一个优点，通常采用简化轨道动力学技术，引入大量经验加速度参数来吸收未模型化的轨道摄动力影响，抑制测量随机误差，提高绝对定轨和相对定轨精度。

本文开展多机构比对融合研究所需的基线产品主要来自NDT和CHS，尽管使用相同的GRACE观测数据，但两家机构所使用的基线处理软件均是自主研制、相互独立的[18-19]。NDT和CHS的基线处理软件的策略描述见表1，由于两个软件在力学模型、模糊度固定、实现方法等方面都有明显差异(见表1)，因此保证了得到的基线产品具有一定的独立性，进行后续的比对融合研究是有意义的。

表1 NDT和CHS基线处理软件的策略Table 1 Strategy of NDT and CHS software packages for baseline determination

3 基线产品比对融合

3.1 互比对

选取2006年01月01日至01月07日一周GRACE双星编队在轨数据作为实验对象，利用两家机构的基线处理软件分别进行独立解算，得到NDT基线产品和CHS基线产品。首先，利用KBR数据分别校核NDT基线产品和CHS基线产品精度，结果如表2所示，NDT和CHS基线产品的KBR校验标准差平均值分别为0.591 mm和0.760 mm，均明显优于1 mm，与目前文献上的GRACE基线处理精度量级相当。其中NDT精度略优，主要原因是考虑了接收天线相位中心变化估计[20-21]。由于KBR 数据自身存在模糊均值未知的问题，其校核的GRACE基线产品精度是在标准差意义下给出的[22]，因此KBR数据无法检核出基线产品中仍可能存在的潜在均值偏移风险。进一步，将NDT与CHS基线产品进行互比对分析(见图4)，发现二者互比对残差的均方根(RMS)在R、T、N以及三维方向分别为0.7、0.9、0.7和1.3 mm，而且二者之间并没发现明显的系统偏差，同时NDT和CHS一周的基线产品互比对分析发现，大约97.86%的基线产品三维互比对残差量级都在2 mm以内(见图5)，该结果表明两个机构的基线产品具有很好的一致性。而且，通过不同机构的基线产品互比对残差大小，很容易识别标记出那些互比对残差较大的时段，便于提醒用户该弧段基线产品可能不可靠，尽量避免使用。对于大多采用相互绕飞的编队模式的分布式InSAR系统，难以通过窄波束的KBR手段实现基线精度校核，此时多机构基线产品互比对分析是获得其基线产品精度和可靠性信息的有效手段。

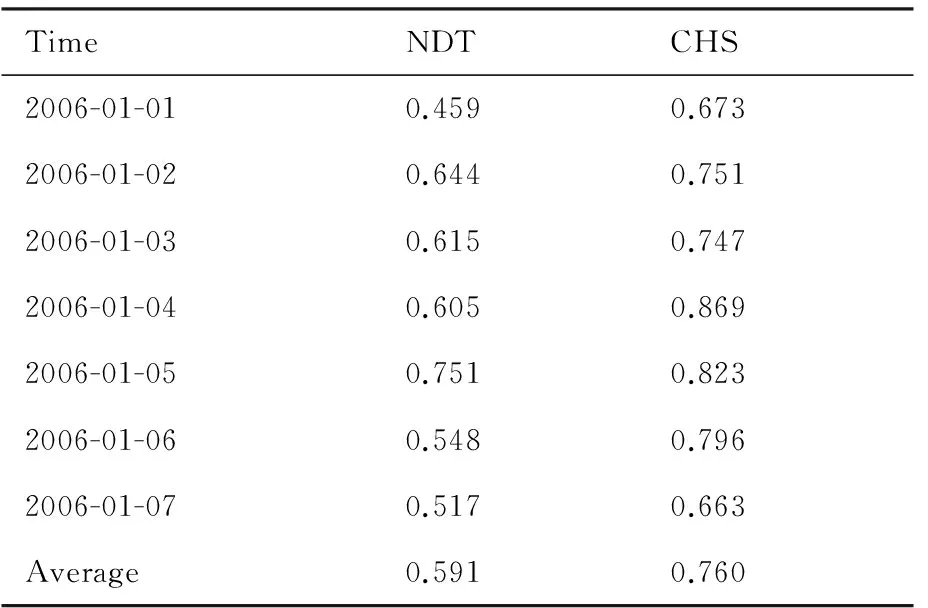
表2 KBR校验标准差Table 2 KBR standard deviation Unit: mm

图4 NDT与CHS的相对定位互比对结果
Fig.4 Comparision between relative position obtained from NDT and CHS

图5 NDT和CHS在3维上的差异
Fig.5 Differences in 3D between NDT and CHS

3.2 融 合

基线互比对分析可有效检测出误差较大的时间段，在此基础上，文中采取的融合策略为对互比对残差超差的时间段不做融合，仅将其标定为超差时间段，不参与 InSAR地理定位产品的解算；对互比对残差未超差的时间段进行加权融合。

将基线产品误差分解为系统误差(均值)和随机误差两部分，NDT、CHS基线产品在R、T、N方向的分量均可表示为

BNDT(t)=B(t)+m1+ε1(t)

(4)

BCHS(t)=B(t)+m2+ε2(t)

(5)

式中：BNDT(t)、BCHS(t)分别为t时刻NDT、CHS的基线产品；B(t)为基线产品的真值部分；m1、m2为基线产品误差的均值部分；ε1、ε2为基线产品随机误差。

将NDT、CHS基线产品进一步加权融合获得融合后的基线产品，简记为“FUSE”。

BFUSE(t)=BNDT(t)×ω+BCHS(t)×(1-ω)=

B(t)+m1×ω+m2×(1-ω)+

ε1(t)×ω+ε2(t)×(1-ω)

(6)

式中：BFUSE(t)为融合后基线产品；ω为融合权值。

从式(6)可见，融合后基线产品的系统偏差仍然为单个机构基线产品系统偏差的线性组合m1·ω+m2(1-ω),并不会被减小。但3.1节NDT、CHS基线产品互比对结果一致性很好，二者之间并没发现明显的系统偏差，这里融合的目的主要是为了进一步抑制单个机构基线产品的随机误差部分。

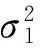
(7)

融合后基线产品的理论方差为

(8)

这里用KBR校验得到的标准差作为单个系统基线产品标准差σ1和σ2的估计，即取σ1=0.591 mm，σ2=0.760 mm(见表2)，代入式(7)得到融合权值ω=0.623。

通过KBR校验FUSE基线产品的精度，其标准差为0.538 mm(见图6)，可见融合基线产品较NDT基线产品精度提高了8.97%，较CHS基线产品提高了29.21%。由于NDT和CHS采用不同的基线处理软件和简化动力学策略，保证了基线产品具有一定的独立性，这使得融合后的基线产品有可能进一步降低原来单个机构基线产品中的随机波动误差。

图7为2006年1月2日三类基线产品的KBR检核残差随时间波动曲线，可见FUSE基线产品KBR检核残差的波动量级相对于单机构产品进一步减小，标准差仅为0.535 mm，该实验表明通过多机构基线产品融合适当提高基线产品精度是可行的。

图6 NDT、CHS和FUSE的KBR校验标准差
Fig.6 KBR standard deviation of NDT, CHS and FUSE

下面进一步分析融合权值选取的合理性。将ω在0～1区间内以0.1为间隔进行遍历，得到不同权值对应的融合基线产品KBR检核标准差(STD)如图8所示。可见，当ω在0.5～0.8区间内时融合基线产品的KBR检核标准差(STD)基本相等，因此ω取0.623是合理的。

图7 2006-01-02 NDT、 CHS和FUSE的 KBR校核残差
Fig.7 KBR residuals of NDT, CHS and FUSE on 2 January 2006

图8 融合基线产品KBR检核标准差随 融合权值的变化
Fig.8 Change of KBR standard deviations of FUSE with change of weight

图9 2007-05-09 NDT与CHS的基线产品 互比对的结果
Fig.9 Differences between GRACE relative position obtained from NDT and CHS on 9 May 2007

图9给出了2007年05月09日NDT与CHS求解的GRACE星间基线3D的互比对结果，图中阴影区域的时间段刚好对应第2节中KBR检核残差超差部分(见图2)，可以看出该阴影区域时间段内的多机构基线互比对结果也同样明显超差。这表明，在缺少外部KBR检核手段的条件下，通过多机构互比对也可以有效识别基线精度较差的时间段，降低单个机构基线产品的不可靠风险。此外，选择阴影区域时间段之外未超差部分的基线产品进行融合(权值不变)，融合后的基线产品KBR检核标准差为0.526 mm，相比同时段的NDT和CHS单机构基线产品，精度分别提高了7.56%和28.53%。

4 结 论

本文研究多机构产品比对融合方法，以提高分布式InSAR编队基线高精度确定的精度和可靠性。

1) 分析了影响基线高精度确定的不可靠因素，星载GPS接收机连续跟踪弧段较短、个别弧段共视GPS卫星个数偏少或模糊度固定成功率偏低、频繁轨道机动等都会造成高精度基线确定的不可靠。

2) NDT和CHS基线产品互比对结果表明，对于缺少KBR校核手段的分布式InSAR系统，可通过不同机构基线产品的互比对分析获得基线产品的精度和可靠性信息，且可准确识别出基线精度较差的时段，避免使用不可靠的基线产品从而提高InSAR地理定位产品的整体可靠性。

同时结果表明NDT和CHS的基线产品具有很好的一致性，互比对残差的均方根在R、T、N方向分别为0.7、0.9、0.7 mm具有很好的一致性，二者之间没有明显系统偏差，大约97.86%的基线三维互比对残差量级在2 mm以内。

3) 使用不同的基线处理软件和简化动力学策略保证了NDT和CHS基线产品具有一定的独立性，融合后的基线产品可进一步降低基线产品中的随机波动误差。KBR校核结果表明融合后基线产品的精度得到了适当提高，分别较NDT基线产品提高8.97%，较CHS基线产品提高29.21%。

[1] DAVID A. Gravity measurement: Amazing GRACE[J]. Nature, 2002, 416(6876): 10-11.

[2] MASSONNET D, ROSSI M, CARMONA C, et al. The displacement field of the landers earthquake mapped by radar interferometry[J]. Nature, 1993, 364: 138-142.

[3] TAPLEY B D, BETTADPUR S, RIES J C, et al. GRACE measurements of mass variability in the earth system[J]. Science, 2004, 305(5683): 503-505.

[4] MOREIRA A, KRIEGER G, HAJNSEK I, et al. TanDEM-X: A terraSAR-X add-on satellite for single-pass SAR interferometry[C]∥2004 IEEE International Geoscience and Remote Sensing Symposium. Piscataway, NJ: IEEE Press, 2004: 1000-1003.

[5] ANTHES R A, BERNHARDT P A, CHEN Y, et al. The COSMIC/FORMOSAT-3 mission: Early results[J]. Bulletin of the American Meteorological Society, 2008, 89(3): 313-333.

[6] AMICO S D, ARDAENS J S, FLORIO S D. Autonomous formation flying based on GPS-PRISMA flight results[J]. Acta Astronautica, 2013, 82(1): 69-79.

[7] CHEN P, SHU L Z, DING R, et al. Kinematic single-frequency relative positioning for LEO formation flying mission[J]. GPS Solutions, 2015, 19(4): 525-535.

[8] 谷德峰. 分布式 InSAR卫星系统空间状态的测量与估计[D]. 长沙： 国防科学技术大学， 2009: 89-114.

GU D F. The spatial states measurement and estimation of distributed InSAR satellite system[D]. Changsha: National University of Defense Technology, 2009: 89-114 (in Chinese).

[9] MONTENBRUCK O, WERMUTH M, KAHLE R. GPS based relative navigation for the TanDEM-X mission-first flight results[J]. Navigation, 2011, 58(4): 293-304.

[10] ANTONY J W, GONZALEZ J H, SCHWERDT M, et al. Results of the TanDEM-X baseline calibration[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(3): 1495-1501.

[11] KROES R. Precise relative positioning of formation flying spacecraft using GPS[D]. Netherlands: Delft University of Technology, 2006: 79-135.

[12] KROES R, MONTENBRUCK O, BERTIGER W, et al. Precise GRACE baseline determination using GPS[J]. GPS Solutions, 2005, 9(1): 21-31.

[14] YOON Y, MONTENBRUCK O, KIRSCHNER M. Precise maneuver calibration for remote sensing satellites[C]∥19th International Symposium on Space Flight Dynamics, 2006.

[15] JU B, GU D F, HERRING T A, et al. Precise orbit and baseline determination for maneuvering low earth orbiters [J]. GPS Solutions, 2015, 21(1): 1-12.

[16] ALLENDE-ALBA G, MONTENBRUCK O. Robust and precise baseline determination of distributed spacecraft in LEO [J]. Advances in Space Research, 2015, 57(1): 46-63.

[18] LIU J H, GU D F, JU B, et al. Basic performance of BeiDou-2 navigation satellite system used in LEO satellites precise orbit determination[J]. Chinese Journal of Aeronautics, 2014, 27(5): 1251-1258.

[19] 秦显平. 星载GPS低轨卫星定轨理论及方法研究[D]. 郑州： 解放军信息工程大学， 2009: 125-135.

QIN X P. Research on precision orbit determination theory and method of low earth orbiter based on GPS technique[J]. Zhengzhou: PLA Information Engineering University, 2009: 125-135 (in Chinese).

[20] MAO X, VISSER P N A M, VAN DEN IJSSEL J. Impact of GPS antenna phase center and code residual variation maps on orbit and baseline determination of GRACE[J]. Advances in Space Research, 2017, 59(12): 2987-3002.

[21] GU D F, JU B, LIU J H, et al. Enhanced GPS-based GRACE baseline determination by using a new strategy for ambiguity resolution and relative phase center variation corrections[J]. Acta Astronautica, 2017, 138: 176-184.

[22] WERMUTH M, MONTENBRUCK O, WENDLEDER A. Relative navigation for the TanDEM-X mission and evaluation with DEM calibration results[C]∥22nd International Symposium on Spaceflight Dynamics, 2011.