多元函数条件极值的一种较精确的充分条件

张 驰，胡 博，秦 琴，钟海全

（1.广东省华立技师学院建筑与经济学部，广州 511300；2.卡斯柯信号有限公司平台软件部，上海 200071；3.广州大学松田学院，广州 511370；4.西南石油大学油气藏地质与开发工程国家重点实验室，成都 610500）

对于无条件极值问题，应采用目标函数的Hesse矩阵作为判别其充分条件的依据，许多教材都有详细的阐述；但对于用拉格朗日乘数法解多元函数条件极值时充分条件的判别矩阵，因其比Hesse矩阵复杂许多，少有教材〔1-3〕详细论述。两种充分条件的判别矩阵具有差别的原因在于：条件极值问题带有等式约束，其驻点处的自变量增量不全为独立变量，即自变量增量间存在约束关系；而无条件极值的自变量增量之间没有约束关系，因而可直接采用Hesse矩阵判定。所以要寻找精确的条件极值的充分条件的判别矩阵，就应求出自变量增量中非独立变量关于独立变量的解析表达式或数值表达式。本文分析了两种充分条件的关联及差别，详细推导了条件极值的充分条件的判别方法；在满足隐函数存在定理的条件下，于驻点处对约束条件作一阶泰勒展开，进而求出非独立变量关于独立变量的解析表达式。本文有助于理解无条件极值和条件极值的充分条件的关联及差别，在此理解上，给出了一种寻找更精确的条件极值的充分条件的判别矩阵的方法。

1 无条件极值充分条件的判别法与条件极值充分条件的判别矩阵

为方便与后文中条件极值的充分条件的判别法作对比，此处先回顾无条件极值的充分条件。设R为实数域，n维欧几里得空间为Rn，即Rn={(x1,x2,…,xn)|x1,x2,…,xn∈R1}，则Rn具有实线性空间的代数结 构 和 距 离 结 构 ：∀x=(x1,x2,…,xn)，y=(y1,y2,…,yn)∈Rn，λ∈R1，有x+y=(x1+y1,x2+y2,…,xn+yn)，λx=(λx1,λx2,…,λxn)，欧氏距离

设目标函数f(x)是定义在Rn中区域Ω上的函数，X0=()是Ω的内点，f(x)在X0的一个邻域内具有二阶连续偏导数，且X0是f(x)的驻点，即∇f(X0)=0；记Hn为f(x)在X0的Hesse矩阵，则有：若Hn正定，则X0是f(x)的极小值点；若Hn负定，则X0是f(x)的极大值点；若Hn的特征值有正有负，则X0是f(x)的鞍点；其余情况，则不能判定X0的状态。

对于求解等式约束条件极值的问题，可转化为求解无条件极值，即拉格朗日乘数法，便可应用求解无条件极值的方法得到驻点，这实际上是一种降维思想〔4〕。虽然乘数法解出的是拉格朗日函数的驻点，但因为可行域内的点均满足等式约束，所以拉格朗日函数的驻点也是f(x)的驻点。

现设n,m∈N+，m＜n，且本文中的f(x)在定义域内对每个自变量xi具有二阶连续偏导数，等式约束有m个：

在驻点及其某一邻域内满足条件Jacobi矩阵行满秩，即式（2），以及满足式（3）

作Lagrange函数：

解这n+m个方程可得驻点。在任一驻点处，显然满足m个等式约束，即；又因为是条件极值问题，所以任一驻点处的任一改变量均应在可行域内，则该驻点处的微小改变量也应满足这m个等式约束，即，则有，则该驻点X0为极小值点；若，则X0为极大值点；若Δf()X有正有负，则X0为鞍点。

对L函数（4）在驻点X0作关于的二阶泰勒展开，此时需将L函数中的看作常量，可得：

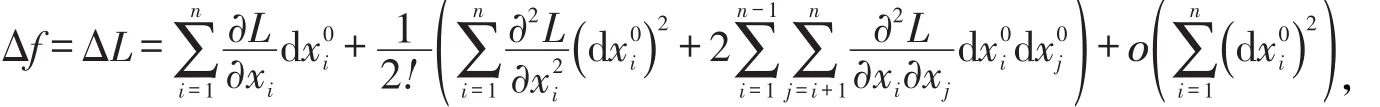
由条件极值的必要性条件〔1，5〕可得：

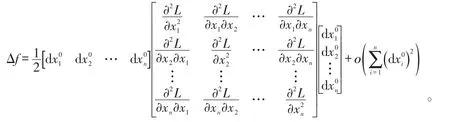
此时Hesse矩阵若仍采用无条件极值的充分条件〔1〕判别，则有：若在该驻点X0处Hn正定，则该驻点为极小值点；若Hn负定，则X0为极大值点；若Hn的特征值有正有负，则X0为鞍点；其余情况，则不能判定X0的状态。无条件极值的充分条件判别法是将n个dx0i均作为独立变量，但对于条件极值，由于存在m个等式约束，则独立变量其实只有n-m个，另外m个变量为这n-m个独立变量的隐函数〔6〕，即为非独立变量，所以需求出非独立变量关于独立变量的表达式才能更精确地判别极值，这是条件极值充分条件判别法与无条件极值充分条件判别法不同的关键。

现在继续讨论条件极值的充分条件的判别方法。对等式约束（1）在满足式（2）及式（3）（即满足隐函数存在定理〔7〕）的驻点X0处作一阶泰勒展开，可得：

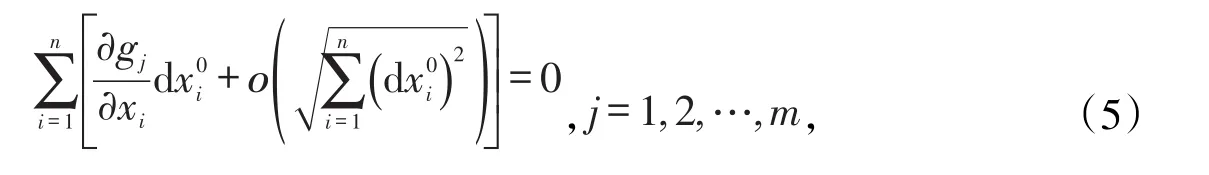
当dxi0足够小，假设，于是解这m个线性方程可得：此时是将作为独立变量，其中记系数矩阵Am×()n-m为：

记单位矩阵In-m为：

记Hesse变形矩阵H∗n-m为：

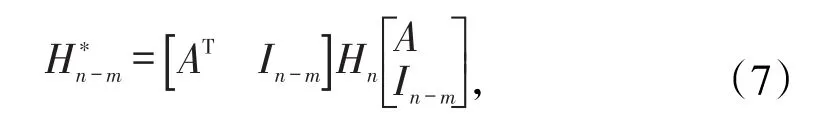
在驻点X0处，当足够小时是二次型的高阶无穷小，则Δf与同号〔8〕；此时若正定的特征值全为正，则所有二次型取极小值，该驻点X0为极小值点；若负定，的特征值全为负，则所有二次型取极大值，X0为极大值点〔9-10〕；若的特征值有正有负，则二次型有正有负，Δf(X)有正有负，X0为鞍点；其余情况，则不能判定X0的状态。

2 条件极值的充分条件的判别矩阵中系数ajk的确定

既然无条件极值采用的判别矩阵Hn与条件极值采用的判别矩阵有所差别，则需求出中系数矩阵Am×(n-m)，即找到ajk的表达式，才能更精确地判别极值。

当n=3,m=2时，目标函数为：f(x1,x2,x3)，等式约束（1）变为式（8），

且L函数（4）在驻点X0处均满足式（2）及式（3）。设此时Jacobi行列式为即以x3作为独立变量，此时i=1,2,3;j=1,2，则对等式约束（8）在驻点处作一阶泰勒展开可得

当n=4,m=2时，目标函数为：f( )x1,x2,x3,x4，等式约束（1）变为式（9），

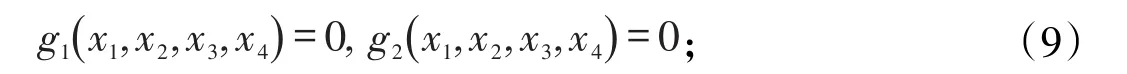
且L函数（4）在驻点X0处均满足式（2）及式（3）。此时设Jacobi行列式为即以x3,x4作为独立变量，此时i=1,2,3,4;j=1,2，则对等式约束（9）在驻点处作一阶泰勒展开可得：

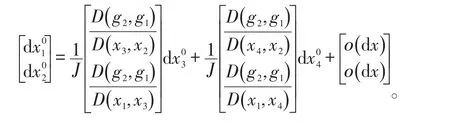
继续求解高维多约束的情形，并由数学归纳法可推知，∀n,m∈N+,m＜n，k=1,2,…n-m，当目标函数为f(x)，等式约束为（1），且L函数（4）在驻点处均满足式（2）及式（3）时，则对等式约束（1）在驻点处作一阶泰勒展开可得如下关系式：

当j=1，即求系数矩阵Am×(n-m)的第一行系数a1k时

例如：

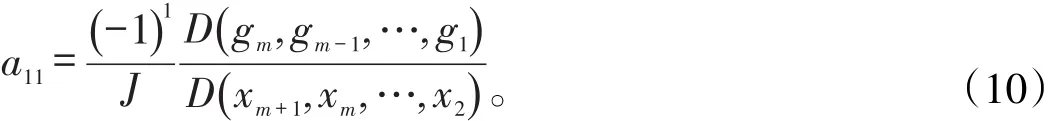
当j=m，即求系数矩阵Am×(n-m)的最后一行系数amk时

例如：

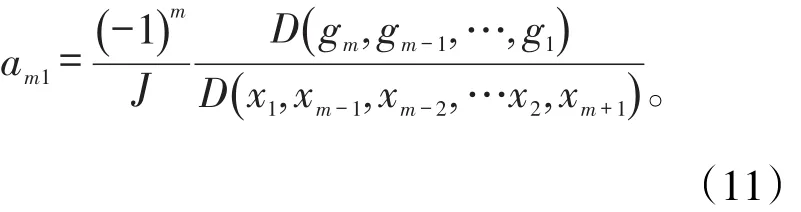
当j=2,3,…m-1，即求系数矩阵Am×(n-m)的中间行系数ajk时，

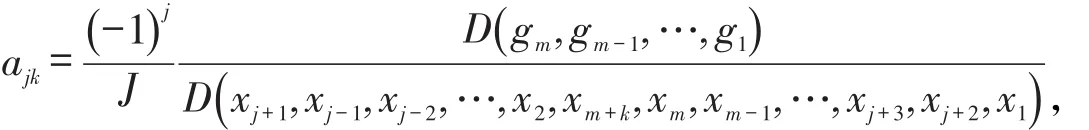
例如，当j=2，即求系数矩阵Am×(n-m)的第2行系数a2k时

系数ajk中分母部分乘积右侧各元素的变化规律为：x共有m个元素：x1,x2,…,xm，其中xj不存在，被xm+k在第j列取代，其余的元素从xm,xm-1,…,xj+3,xj+2,x1依次排列在xm+k右侧，xj+1,xj-1,xj-2,…,x2依次排列在xm+k左侧。需要注意的是，若ajk中各元素排列顺序发生变化，则ajk的正负符号可能发生变化：当变动奇数次时，符号改变；当变动偶数次时，符号不变；其中变动次数指各元素按相邻顺序依次变动的次数。

3 应用举例：采用Hn与判别条件极值的差别

此处应用与文献〔6〕中相似的例子来验证条件极值的充分条件应采用Hn∗-m而不是Hn来判别极值。设笛卡尔坐标系中有椭圆方程，

求该椭圆上的点到坐标原点距离的极大值和极小值。由题可知，式（12）是以坐标原点为顶点，y轴为转轴的旋转抛物面；式（13）是过（1，0，0），（0，1，0），（0，0，1）三点并以（1，1，1）为一法向的平面；二者交线为一椭圆，其上点到原点的距离必存在极大值和极小值。或者可采用文献〔6〕中初等数学的方法证明极大值和极小值的存在。

解：原题等价于求目标函数f(x,y,z)=x2+y2+z2在等式约束g1(x,y,z)=y-x2-z2=0，g2(x,y,z)=x+y+z-1=0下的极大值和极小值。作L函数L(x,y,z,λ1,λ2)=f+λ1g1+λ2g2，由条件极值的必要性条件〔5，7〕可得L函数的两个驻点分别为：

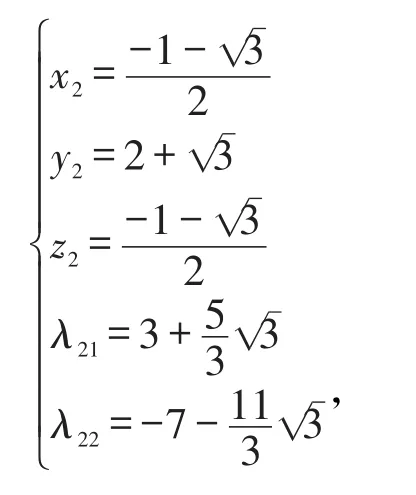
4 结论

第一，对于无条件极值的充分条件，应采用Hesse矩阵Hn作为判别矩阵；对于条件极值的充分条件，应采用Hesse变形矩阵作为判别矩阵，可判别出一部分本身是极值点但被Hn错误判定的驻点。产生该差别的原因是条件极值问题的自变量增量dxi均需满足m个等式约束，所以n个dxi中只有n-m个是独立变量，另外m个非独立变量为这n-m个独立变量的隐函数；而无条件极值中n个自变量增量均是独立变量。

第二，对于条件极值问题，虽然采用判别驻点比Hn更精确，但本文给出的解析表达式仍不能判别出任一条件极值问题的所有驻点的信息。原因在于式（5）是对等式约束在驻点处作一阶泰勒展开得到的关系式，舍弃了二阶及其以上的高阶无穷小，所求解出的非独立变量关于独立变量的表达式并不是最精确的。随着目标函数维数增加，等式约束数目增多、复杂程度增大，求解式（5）已经很困难；如果再对等式约束作高阶泰勒展开，解析表达式将更难或者无法解出。若想找到自变量增量间更精确的关系式，需对式（5）作高阶泰勒展开直至高阶无穷小量为零或近似为零，然后使用数值计算软件求解出它们间的数值关系式，从而找到更精确的Hesse变形矩阵，方能更精确地判别出驻点的信息。虽然得不到自变量增量间最准确的解析表达式，但该判别法仍具有理论价值：指明了条件极值与无条件极值的充分条件的判别矩阵的关联及差别，在此基础上，给出了高维多约束状态下一种寻找更精确的条件极值的充分条件的判别矩阵的方法。