基于学校满意度的院系两级排课问题数学模型

杨子兰，李 睿，杨慧娟

（1.云南大学旅游文化学院信息科学与技术系，云南丽江 674199；2.昭通学院数学与统计系，云南昭通 657000）

随着教育的不断改革，高校的不断扩招，排课问题变得越来越复杂。排课的主要任务就是根据学校每学期的开课计划，针对全校不同类型学生的所有课程的时间、地点以及授课教师进行合理安排，确保不发生冲突。早在20世纪50年代末，国外就有人开始研究课表编排问题。到1975年S.Even和Cooper等人将排课问题理论化，证明了排课问题是NP-完全问题〔1〕，当问题的规模增大时，其复杂度呈指数增长，在一般的实际情况中不可能准确地求出最优解。我国对于排课问题的研究始于20世纪80年代。1984年，林章希和林尧瑞发表了在排课问题上的实验性研究成果〔2〕。由于每个学校的实际情况不同，目前还没有一个可以通用的排课算法。近年来排课问题备受关注〔3-9〕，越来越多的学者采用了捆绑式排课的方法〔5，9〕。随着高校的不断发展，目前，很多高校具有多校区、多教学楼等特点，为适应高校的发展需求，越来越多的学校采用院系两级共同排课的模式。鉴于此，根据院系两级教务共同排课的特点，将教师、教学班级、课程捆绑成一个教学任务单元，拟建立基于学校满意度的院系两级排课问题数学模型。

1 问题描述

基于院系两级任务的排课问题实质上是指由学校教务处和系部相关工作人员共同完成的排课问题：由各个系完成教学计划，开课系部指定任课教师；公共类课程由教务处统一安排授课时间及地点，专业类课程由学生所在系部安排授课时间及地点。院系两级共同排课模式比传统排课模式更灵活、高效。由于每个学校某学期的开课计划中已经安排好某教师上某班的某门课程的信息，故排课过程中可以直接利用这些数据资源。利用捆绑式排课的方法，即将教师集合、教学班级集合、课程集合捆绑成一个教学任务计划单元，教室集合为一个单元，时间集合为一个单元。由此，排课问题就变成在时间和空间资源上合理安排教学任务单元的问题。故可对传统的排课问题的硬约束条件进行简化，得：（1）同一个时间点，同一个教学任务单元最多安排在同一个教室上课；（2）同一个教学任务单元中的教学班人数不超过其授课教室的最大容量；（3）同一个教学任务单元中的教学课程的课时数必须等于该门课程的课时要求。

2 时间段编号

为得到较好的数学模型，根据学校的教学时间段，对时间段进行编号，具体如下：将一周分为5个工作日，每天设为5个时间段，分别为上午8：30～10：10为1～2节课；上午10：30～12：10为3～4节课；下午2：00～3：40为5～6节课；下午4：00～5：40为7～8节课；下午7：00～8：40为9～10节课。这样，每周5天，且周五下午不安排课，则5天工作日共有23个时间段。为了方便，特将23个时间段划分为5种类型，并进行编号，见表1。

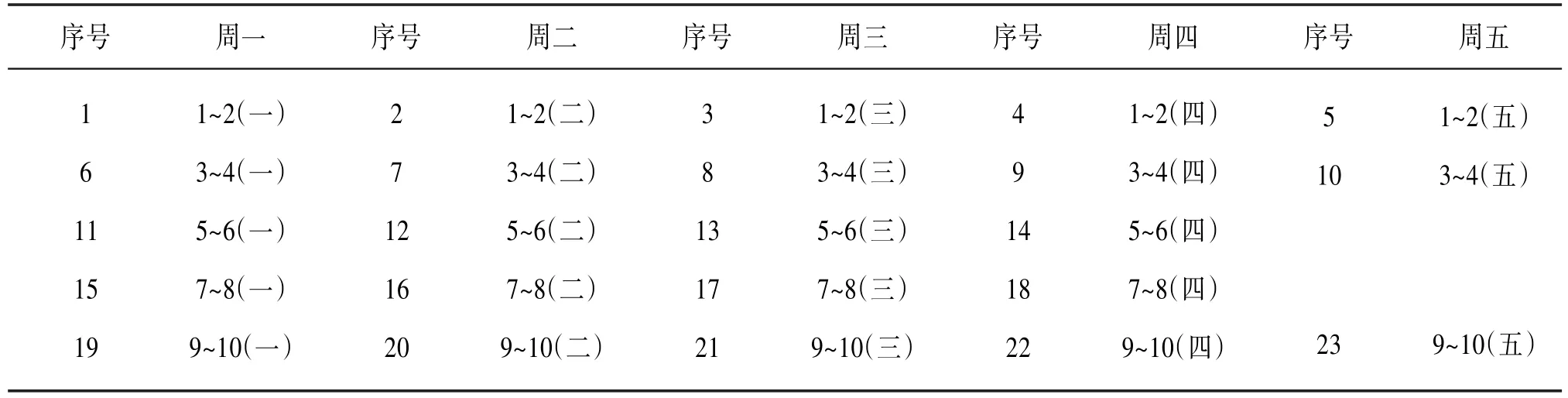
表1 时间段编号

3 变量说明

假设某高校属于院系设置，目前有m个系，n个授课教师。根据院系两级共同排课的特点，将教室资源划分到各个系（即每个系都有专用教学教室），且已经对教室进行编号，则变量说明如下：

设教师集合表示为T={T1,T2,…,Ti,…,Tn}（n个教师）；教室集合表示为（其 中Ri=表示第i个系的教室集合，表示第i个系的第|Ri|个教室 ，且对应的教室容量为） ；课程集合表示为C={C1,C2,…,Cq（}q门课程，且与C对应的q门课程的周学时数依次为l1,l2,…,lq）；时间段集合表示为π={1,2,…,23（}23个时间段）；自然班级集合表示为（其中表示第i个系的第j个自然班级，对应的人数为sij）。

4 建立0-1整数规划数学模型

一般情况下，在排课工作开始前，院系两级教务已经制定好教学计划，根据教学计划，已将教师和学生分配给课程，因此可利用捆绑式排课的方法，即将教师集合T、教学班级集合S（假设不存在合班上课的情况）、课程集合C捆绑成一个教学任务计划单元TSC（假设TSC中的教学任务计划单元已按课程重要程度划分为专业核心课程、专业基础课程、专业选修、公共必修课、公共选修课等，且教学任务单元的总数为|TSC|，针对|TSC|个教学任务计划单元对应的教学班级集合表示为其中表示第i个系的第j个教学班级，对应的人数为sij），教室集合R为一个单元，时间集合π为一个单元。因此，排课的主要问题变成了如何安排时间段和教室，实现某时间段某教学任务单元最多对应一个符合需求的教室，即遵守上述约束条件。设TSC中有N1个教学任务计划单元包含公共必修课，有N2个教学任务计划单元包含公共选修课，|TSC|-N1-N2个教学任|TSC|-N1-N2＜i≤|TSC|时，取yijt=0）。

针对包含公共课的N1+N2个教学任务计划单元而言，同一个时间段，同一个教室至多安排一个务计划单元中包含mi′个第i个系的教学任务计划单元。因此，排课的主要问题变成了如何安排时间段和教室，实现某时间段某教学任务单元最多对应一个符合需求的教室，即遵守上述约束条件。为方便建立数学模型，针对包含公共课的N1+N2个教学任务单元而言，引入三维0-1决策变量xijt，当第i个教学任务计划单元在第t个时间段在第j个教室上课时xijt=1，否则xijt=0（且规定当N1+N2＜i≤| |TSC时，取xijt=0）。针对不包含公共课的| |TSC-N1-N2个教学任务计划单元而言，引入三维0-1决策变量yijt，当第i个教学任务计划单元在第t个时间段在第j个教室上课时yijt=1，否则yijt=0（且规定当教学任务单元授课，用数学式子表示为

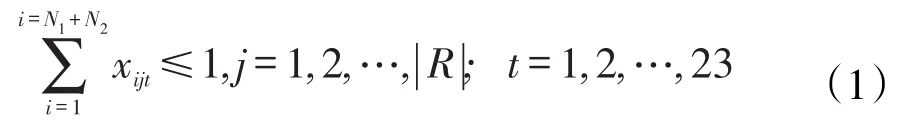
针对不包含公共课的第i个系的mi′个教学任务计划单元而言，同一个时间段，同一个教室至多安排一个教学任务单元授课，则用数学式子表示为

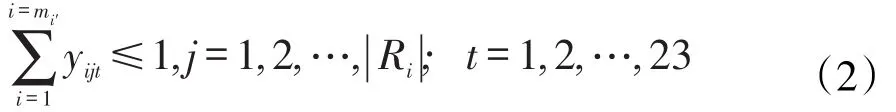
则针对m个系而言，同一个时间段，同一个教室至多安排一个教学任务单元授课，则用数学式子表示为

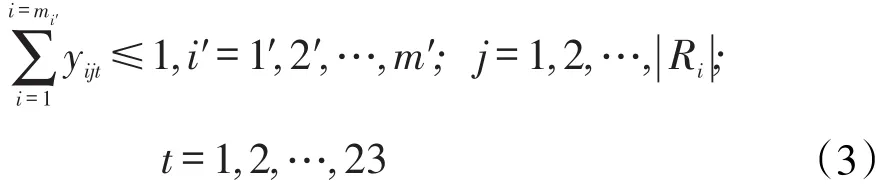
要使（1）、（3）式中的教学任务单元及教室资源不发生冲突，即教学任务单元授课时间不发生冲突，则必须满足

每周内每个教学任务计划单元对应的课程授课时间要等于该门课的周课时，因此，包含公共课的N1+N2个教学任务单元中，每周内每个教学任务计划单元对应的课程授课时间等于该门课的周课时的数学式子表示为

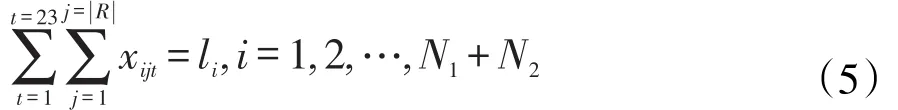
不包含公共课的第i个系的mi′个教学任务单元中，每周内每个教学任务单元对应的课程授课时间等于该门课的周课时的数学式子表示为

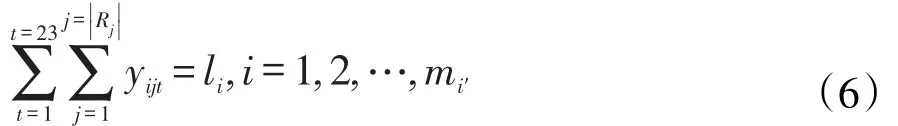
故针对m个系而言，每周内每个教学任务单元对应的课程授课时间等于该门课的周课时的数学式子表示为

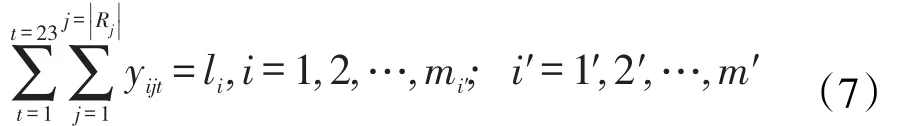
针对包含公共课的N1+N2个教学任务单元而言，第i个教学任务单元在第j个教室授课时需满足该教学班级人数ci不超出教室j的容量rj可用数学式子表示为

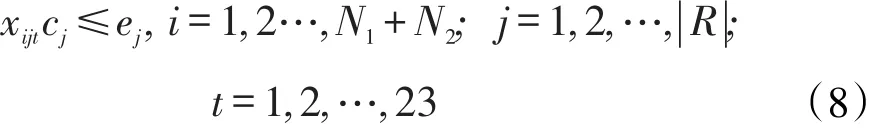
针对不包含公共课的m个系而言，第i个教学任务单元在第j个教室上课时需满足该教学班级人数ci不超出教室j的容量rj可用数学式子表示为

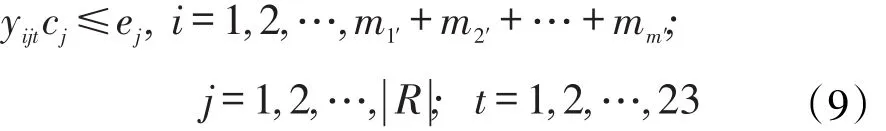
从学校的角度考虑排课问题，在院系两级共同排课下，既要考虑开课计划得以实现，又要考虑把课程安排在学生学习效果较好的节次中，甚至还要考虑减少教学支出等因素。减少教学支出，意味着要充分合理地利用教学资源。

〔4〕中的方法，用Bj′(j′=1′,2′,3′,4′,5′)表示课程的重要程度，也称为权重，把课程划分为专业核心课程、专业基础课程、专业选修、公共必修课、公共选修课。为了体现出重要程度，假设其权重依次赋值为 4、3、0.6、2、0.4。用wt′(t′=1′,2′,3′,4′,5′)表示一天中的5个时间段的课时质量，其中当t′=1′时w1′=1表示第一个时间段（ 即第1、2节）的教学质量，故当1≤i≤5时有wi=1；当t′=2′时，有w2′=0.8表示第二个时间段（即第3、4节）的教学质量，故当6≤i≤10时，有wi=0.8；当t′=3′时，有w3′=0.6表示第三个时间段（ 即第5、6节）的教学质量，故当11≤i≤14时，有wi=0.6；当t′=4′时，有w4′=0.3表示第四个时间段（ 即第7、8节）的教学质量，故当15 ≤i≤ 18时，有wi=0.3；当t′=5′时，有w5′=0.1表示第五个时间段（ 即第9、10节）的教学质量，故当19≤i≤23时，有wi=0.1。对第i个教学任务单元分配教室j时，教室利用率为对应的教学班级人数si除以教室j的容量ej，即

设用Bi表示与第i个教学任务单元相对应的课程的权重。以比较重要的课程最大程度地安排在授课效果较好的节次中且教室资源利用率尽可能地大为目标函数作为学校对排课满意度的衡量指标，得出三维的0-1整数规划模型如下：

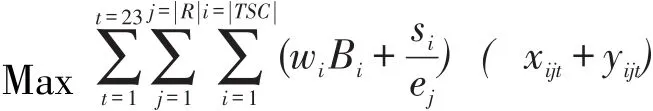
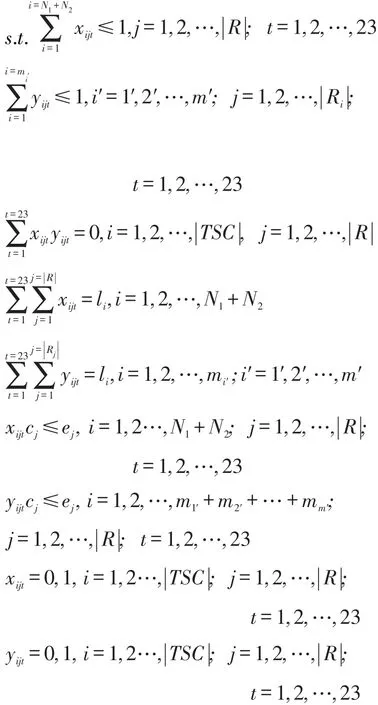
5 结束语

排课问题是NP-完全类问题，很难找到多项式时间算法。通过深入分析院系两级共同排课的特点，将教师、班级、课程捆绑成一个教学任务单元集合，简化了排课问题的硬约束条件。在建立模型的过程中，引入两个三维的0-1变量，并将比较重要的课程尽可能地安排在授课效果较好的节次中且教室资源利用率尽可能地大为目标函数作为学校对排课满意度的衡量指标，建立基于学校满意度的0-1整数规划数学模型，可为研究院系两级共同排课问题的学者提供一定的理论参考。如何设计求解该0-1整数规划数学模型的算法是今后将要开展的进一步工作。

［参考文献］

〔1〕 EVEN S，ITAI A，SHAMIR A.On the complexity of time table and multi-commodity flow problems〔J〕.Symposium on Foundations of Computer Science，2008，5（5）：184-193.

〔2〕林漳希，林尧瑞.人工智能技术在课表编程中的应用〔J〕.清华大学学报（自然版），1984，24（12）：1-8.

〔3〕宗薇，赵光甫.高校智能排课系统算法的研究与实现〔J〕.计算机仿真，2011，28（12）：389-392.

〔4〕杨彦明，岳翠翠，李其申.军队任职院校排课问题的数学建模〔J〕.计算机与现代化，2012（11）：14-17.

〔5〕张丽丽，许峰，胡娟.基于三维立体遗传编码设计的排课系统〔J〕.重庆工商大学学报（自然科学版），2014，31（7）：9-13.

〔6〕叶碧虾.遗传算法在排课系统中的优化研究〔J〕.吉林师范大学学报（自然科学版），2014，35（2）：185-187.

〔7〕 LIMKAR S，KHALWADEKAR A，TEKALE A，et al.Genetic Algorithm：Paradigm Shift over a Traditional Approach of Timetable Scheduling〔C〕∕∕Proceedings of the 3rd International Conference on Frontiers of Intelli⁃gent Computing：Theory and Applications（FICTA）2014.Springer International Publishing，2015：771-780.

〔8〕王璐，杨亚伟.一种改进的遗传算法在年度排课问题中的应用〔J〕.计算机与数字工程，2016，44（8）：1619-1624.