利用石油产品调合关系设计能力验证方案

李 怿，吕大伟，白正伟

（国家燃料油质量监督检验中心，洛阳471003）

能力验证是国际通行的实验室及其监管者实现质量控制的有效方法，串通现象的存在使能力验证计划实施的结果存疑，严重困扰着组织者、参加者以及实验室的客户。本文利用石油产品调合规律，设计了一种能够尽可能多的向能力验证计划参加者分发不同样品的方案以避免串通现象。验证结果表明：依据两组分调合的数学关系，利用稳健回归技术等手段能够有效表征实验室的检测能力，避免串通。

1 能力验证的意义

能力验证是利用实验室间比对，按照预先制定的准则评价参加者能力的活动［1］。其源于实验室管理者因担心实验室检测的准确性，自发进行的多个实验室间的比对活动，目前已成为国际通行的实验室质量控制方法之一，是提高实验室能力建设的有效手段以及保证实验室质量控制的有效方法，同时也是各国及组织广泛采用的评价实验室检测能力的重要技术手段，是实验室认可活动不可或缺的一部分。

2 能力验证活动中的串通

虽然实验室在参加能力验证时均做出了诚实守信的书面承诺，但经常发现有参加者出于提高实验室声誉或由于其内部奖惩机制等原因，存在串通或伪造数据的情况。

目前实验室串通的方式有两类：一类是参考或采用另一个实验室的数据；另一类是收集尽可能多的参试实验室的“原始”检测数据，按照常规的统计评价方法进行计算后将得到的统计量作为实验室结果上报组织者，这种方式常见于小样本量的能力验证活动中，主要表现为能力评定标准差大大小于标准方法规定的再现性限的要求。

依据串通结果得到的统计量必然是不科学的，尤其在小样本量的能力验证活动中，这种影响尤为显著。而依据不科学的统计量进行评价会对能力验证计划的实施造成严重的伤害：它可能使有问题的实验室得到了一个虚假的可信度和影响力，从而不恰当地引导了消费者；它还可能使一个运转正常的实验室受到不应该的名誉损失，且被迫投入大量的质量成本去寻找本不存在的“问题”。

3 处理问题的基本思路

串通的存在对能力验证计划的实施造成了严重的影响，能力验证计划的组织者应采取合理的措施保证从根本上杜绝串通现象的发生。这些措施应该能让想串通或者想伪造数据的实验室感觉其通过串通得到满意结果的可能性比自己的结果更小从而抑制其进行串通的心理。为此有人提出了制备2个浓度相近的样品，并将其随机分发的办法，并从概率的角度进行了证明［2］。但是这并不能有效防止第二类串通方法，且在小样本量的能力验证活动中，会因样本数量的减少而使统计结果的稳健性下降。

本文尝试了一种在能力验证计划中尽可能多地制备、分发不同的样品，使不同实验室得到的样品尽可能不同，从而彻底避免串通的方法。

4 能力验证方案的设计

石油产品的调合，调合产物（X）的某一理化性质（CX）可以用两个调合原料的相关性质（CA，CB）及其各自的质量（mA，mB）或体积分量通过适宜的函数进行描述［3］，对两个固定的调合原料，因为CA，CB是常数，且mA与mB的和为1，则调合后油品的性质（Cx）仅由mA或mB一个自变量决定，即Cx＝f（mB）。

这就给出一个提示：在能力验证方案设计时可利用调合规律，即用两个原料按照不同的配比调配出多个样品，随机编码后发给不同的实验室，收集数据后按照既定的调合规律进行回归分析，得到回归方程，进而得出不同调合比例样品对应的合理估值，将其与实验室报告值比较，从而判断实验室的检测能力。由于实验室得到不同样品的可能大大增加，甚至每个实验室得到的样品都有可能不同，实验室进行串通的可能基本杜绝。

燃料油中心受主管业务部门的委派，于2016年组织了由30多个实验室参加的石油产品部分检测项目的能力验证活动。在该活动中，组织方以干扰样的方式按上述思路向各实验室分派了相应的样品，并回收了数据。基础样（A样）为市售汽油，其作为常规方案的能力验证测试样向实验室分发，并按照相应标准进行统计评价［4］，干扰样为基础样加入不同比例的调合组分（化学纯甲苯，B样），按照上述思路进行了验证。

调合实践中有两种情况：一种是f（mB）可以明确推导得出，如硫含量、苯含量等；另外一种是f（mB）不是明确推导得出，而是由统计分析或以往的经验得出，如馏程、冷滤点、辛烷值等。以下分别以硫含量和辛烷值为代表进行讨论。

4．1 f（mB）可以明确推导得出的情况

4．1．1 硫含量与调合比例的数学关系

2个油品A和B，其中硫的质量浓度分别为ρA和ρB，不同质量分数（wA，wB）的样品配制为新样品X的质量浓度ρX见公式（1）：

因为是两组分调配，所以wA＋wB＝1，ρA和ρB是参与调合油品的固有性质，化简上式，得公式（2）：

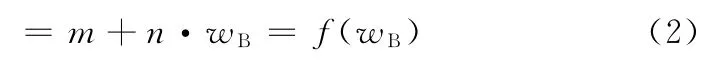
式中：m，n为常数。

调配所得样品的待测参数为样品质量分数的一元一次函数，其中，质量分数wB是一个可以准确得到的参数，m和n是只与参与配制样品有关的常数，且与两个原料的硫含量相关。

4．1．2 结果及影响估值不确定度的因素

影响调合样品估值不确定度的因素有：① 影响检测标准再现性限的相关因素；② 异常值；③ 待测量与B样调入量的数学关系的假设是否有效。

其中因素①与参加能力验证活动的实验室整体能否正确实施检测标准有关，是所有能力验证活动的假设前提，本文不做进一步的讨论，认为前提成立。

对异常值（因素②）的识别和处理是统计技术的一个重要命题，采用建立在最小二乘法基础上的传统线性回归分析。当实际观测值包含异常值时，误差将不再服从正态分布，对这样的数据进行回归分析时，回归直线可能与真实的回归线相差较远，这时估计出的参数是不准确的。解决这一问题的方法有两个：一是运用合适的算法将数据中离群值识别并加以处理，之后再用传统的统计方法来处理；二是采用对离群值不敏感的稳健回归方法［5－6］。本文采用Matlab软件提供的Robustfit函数进行迭代最小二乘法的稳健计算，权重函数和调节参数选用系统默认值。

A样的稳健平均值、稳健标准差、极差依次为33．9，1．86，7．7。调合样品中硫检测的结果汇总见表1。表1中：SR为检测标准规定的再现性要求（以标准偏差形式表示）；Z′为测试结果的评定指标；W为权重。回归方程为ρ预测＝32．29－11．76×wB，回归标准差为0．720 4，常数项p检验值为9．84×10－45，系数p检验值为1．12×10－4。

表1 硫检测项目的结果汇总Tab．1 Summary of sulfur detection item

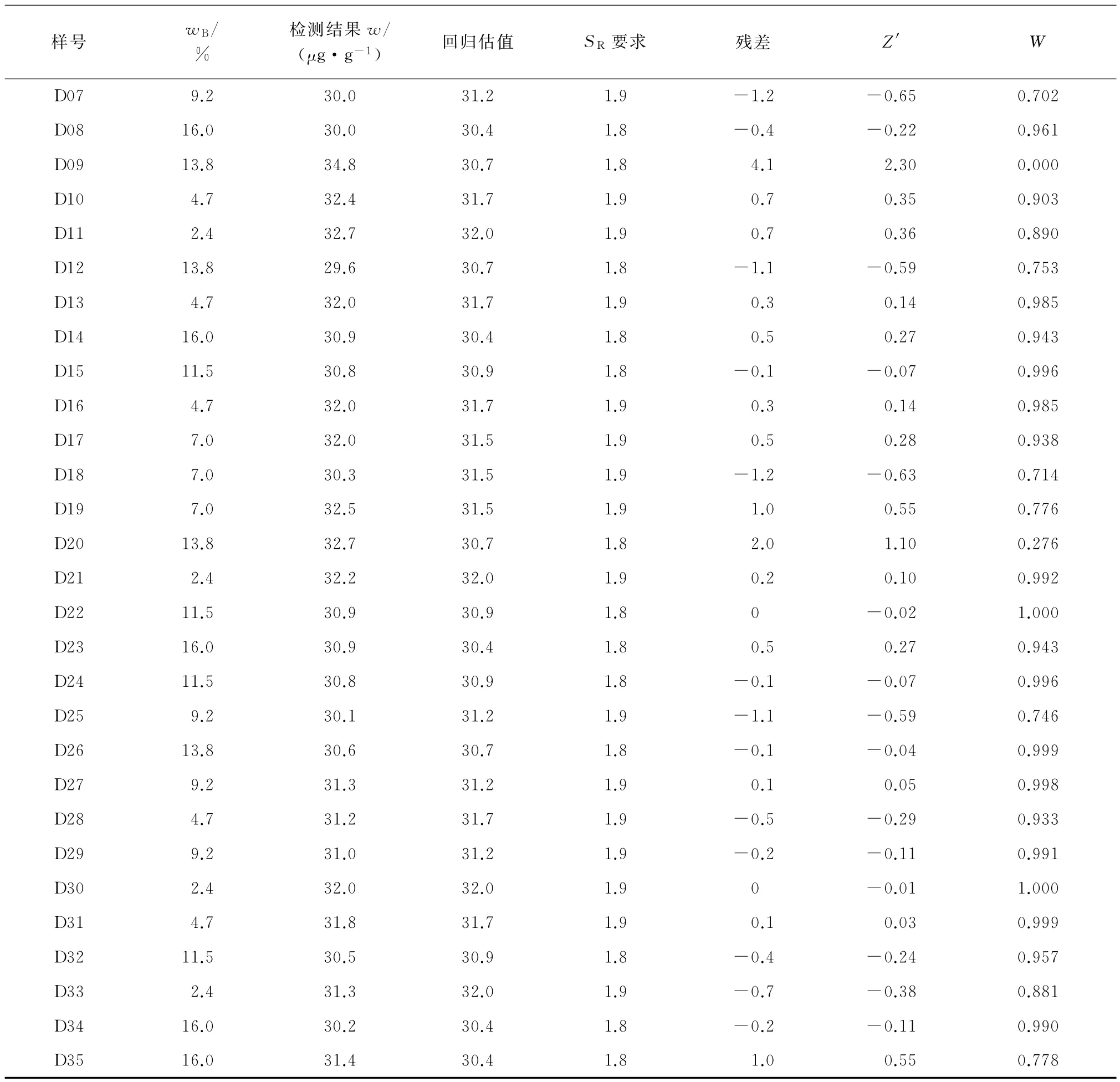
表1（续）

由表1中残差和权重数据发现：选择的函数很好地处理了极端值的问题，部分极端值被赋予了较低的权重，甚至权重为零，结合其他统计分析结果，说明稳健回归结果充分可信，且在抵御离群值影响方面有相当的优势。

线性调合（因素③）是硫含量等标准自身的前提，同时还可用回归分析的结果以及A样的稳健分析结果进行验证：①回归方程的p检验值远低于0．001，即回归方程总体代表性犯错的概率很低，显示回归方程可靠，与线性关系的假设前提吻合；② 回归方程的常数项与A样结果的差在一个标准差范围内，基本可以认为在试验条件下两者一致，与之前的推导吻合；③ 回归标准差小于检测标准规定的再现性标准差，说明回归过程未引入不可接受的不确定度因素。

4．1．3 实验室数据质量的评判

通常，能力验证活动中实验室数据质量的评判由公式（3）决定：

即评定指标Z比分数等于参加者结果减去指定值后除以能力评定标准差，其中能力评定标准差可以由规定值、经验预期值、一般模型、精密度试验结果、一轮能力验证计划所得数据等确定，本文选用精密度试验结果确定能力评定标准差。

图1是参加者A样Z值（常规方案）和调合样Z′值（本方案）的关系图。

图1 硫检测项目中Z值和Z′值的关系图Fig．1 Relationship between Zand Z′in sulfur detection item

由图1可知：两者在评价实验室检测能力上有明显的一致性，说明新设计的能力验证方案同样能够有效地表征实验室的检测能力。

4．2 由统计分析得出待测量的调合关系

4．2．1 辛烷值与调合比例的数学关系

当调合样品的待测量与调合比例的数学关系不能由理论推导得出时，需要根据前人经验或试验数据得出。图2是调合样品的研究法辛烷值与调合样品中B样体积分数（φB）的关系图，其中横坐标是B样在调合样品中的体积分数，纵坐标是实验室报告的相应的调合样品的研究法辛烷值（RON）。

图2 研究法辛烷值与B样体积分数的关系图Fig．2 Relationship between RON and volume fraction of sample B

由图2可知：虽然有一定的分散，但是用一元线性模型描述调合关系是恰当的，即RONX＝f（φB）＝m＋n·φB。

4．2．2 结果及讨论

影响调合样品估值不确定度的因素有3点，与4．1．2节相同。其中因素①、②的讨论内容与4．1．2节相同，不再做讨论。

A样的稳健平均值、稳健标准差、极差依次为94．2，0．12，0．5。调合样品研究法辛烷值项目的结果汇总见表2。表2中：回归方程为 RON预测＝94．34＋0．139 5×φB，回归标准差为0．267 1，常数项p检验值为1．47×10－74，系数p检验值为6．25×10－14。

表2 研究法辛烷值项目的结果汇总Tab．2 Summary of RON item

表2（续）

对表2中数据进行分析发现：① 回归预测方程的p检验值远远低于0．001，即回归方程总体代表性犯错的概率很低，显示假设的数学关系可靠；②本例中回归方程的常数项与A样统计结果一致，两者之差为再现性标准偏差的一半，可以认为在试验条件下，两者基本一致，暗示A样和调合样在试验范围内的调合符合线性调合规律；③ 回归标准差与检测标准规定的再现性标准差相当，说明回归过程未引入不可接受的不确定度因素。以上3点说明：在试验条件下，选择一元线性模型描述研究法辛烷值的调合关系是恰当的。

与4．1．3节一样，选用精密度试验结果作为能力验证标准差的来源。图3是参加者A样Z值和调合样Z′值的关系图。

图3 研究法辛烷值项目中Z值和Z′值的关系图Fig．3 Relationship between Zand Z′in RON item

由图3可知，两者一致性不佳。但是分析后发现：① 在常规方案实施中提交了可疑结果的某实验室在本方案中被评定为满意，不过考虑到常规方案中能力评定标准差为0．12，调合方案中能力评定标准差为0．25，两者偏离指定值的程度基本一致；②在常规方案中性能统计量为0的多个实验室，在本方案中显示出较大的差异，表明本方案能够较好地区分实验室的检测能力；③ 部分在常规方案中提交了满意结果的实验室在本方案中表现为可疑或不满意，不满意和可疑实验室为8．6%，进一步表明，本方案能够较好地区分实验室的检测能力。

本文尝试利用石油产品的调合特性，设计了一种尽可能多地制备、分发不同样品的能力验证方案，使参加活动的实验室得到的样品不同，以彻底避免串通。

本文所用方法属于新方法，还需要积极地积累数据，以便进一步提高其有效性和适用性。

［1］ CNAS－RL 02：2016 能力验证规则［S］．

［2］ 柳乃奎．统计方法在抑制能力验证计划的数据串通问题中的应用［J］．理化检验－化学分册，2013，49（8）：988－990．

［3］ 侯祥麟．中国炼油技术［M］．北京：中国石化出版社，1991．

［4］ GB／T 28043－2011 利用实验室间比对进行能力验证的统计方法［S］．

［5］ 谢玉珑，王继红，梁逸曾，等．化学计量学中的稳健估计方法［J］．分析化学，1994，22（3）：294－300．

［6］ 梁逸曾，周声劢，崔卉．多元分析的稳健方法［J］．化学通报，1996（6）：26－31．