果蔬气调库快速降氧时间的影响因素

周 博， 南晓红

（西安建筑科技大学 环境与市政工程学院，陕西 西安710055）

气调贮藏是目前最先进的果蔬保鲜贮藏方式，它在冷藏的基础上增加气体成分调节，采用专门的降氧设备，使库内的氧气浓度迅速降低至规定的指标，有效抑制果蔬的呼吸作用，达到尽量延长果蔬贮藏时间的目的。为了使果蔬的贮藏环境尽快达到气调指标，作者对气调库快速降氧时间的影响因素进行了研究。

影响气调库降氧时间的因素有：制氮机制氮能力和工作参数、贮藏果蔬的多少、果蔬的品种以及气调库的气密性等。由于影响降氧时间的因素较多，而且降氧过程持续时间长，如果采用实验研究将会消耗大量的财力、物力以及人力。计算流体力学（CFD）是基于计算机技术的一种数值计算工具，克服了传统理论分析法在对象简化和计算求解方面的不足，突破了试验过程人力物力消耗以及试验周期长等诸多限制[1]。因此，关于冷库内气流组织的研究多采用CFD的方法。目前，国内外利用CFD软件关于冷库内气流组织的研究多集中于普通冷库内气流速度场和温度场[2-11]，关于气调库的研究则较少。文献[12-14]运用CFD软件对影响气调库内气流组织的多个设计参数进行数值分析，为合理设计气调库内的气流组织和优化气调库设计提供了参考依据。但是对气调库降氧过程的研究不够深入，而且研究成果难以推广到其它气调库。

作者利用CFD软件建立了通用的气调库内气体组分浓度数值计算模型，该计算模型适用于求解气调库不同阶段的气体组分浓度分布和变化情况。为了使模型尽量与实际情况相一致，作者通过编译User-Defined Function（UDF）程序来解决冷风机送风口边界的各气体组分质量分数和苹果的呼吸强度随库内气体组分浓度的变化而改变这两个问题，并将计算结果与文献 [15]（其实验气调库与本研究对象为同一气调库）的实验结果进行对比。

1 物理模型

主要研究气调库内快速降氧过程，这一过程是通过充入高纯度的氮气置换库内气体使氧气浓度降至所需要的值来实现的。作者以西安某苹果气调库为研究对象，气调库模型见图1。库体尺寸（长宽高）为8.0 m×4.6 m×6.5 m，货物堆放方式为一堆，尺寸（长宽高）为6.0 m×3.6 m×5.5 m。该气调库氮气充注管道和库内气体出口管道直径均为0.15 m。

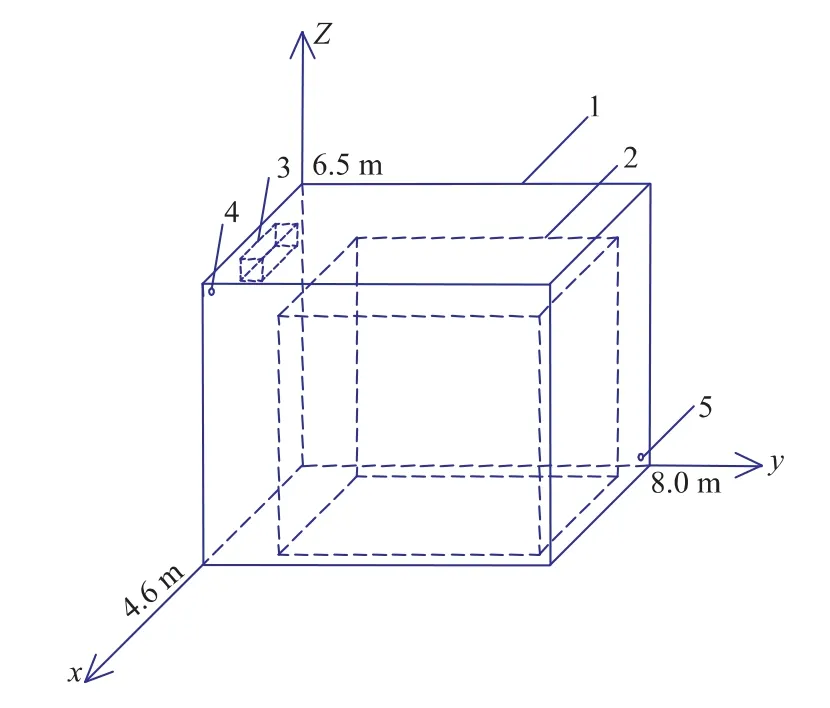
图1 气调库物理模型Fig.1 Physicalmodel of CA room

2数学模型的建立

2.1 紊流模型的选择

采用k-ε湍流模型和组分输运模型，该模型的控制方程包括连续性方程、动量方程、能量方程、组分浓度方程、k方程及ε方程。模型控制方程的通用形式如下：

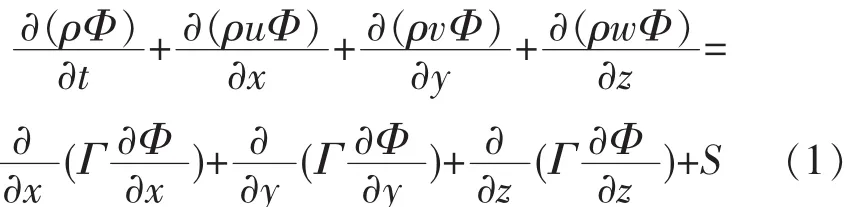
式中，Φ为通用变量，Γ为广义扩散系数，S为广义源项。

2.2 气体区数学模型的建立

进行计算时，对气调库内气体区作出如下假设：气调库内气体为牛顿流体；气体在流动过程中是不可压缩的；库内气体不参与辐射；气体物性参数为常数。

k-ε湍流模型求解气体区控制方程用到的参数见表1。的建立

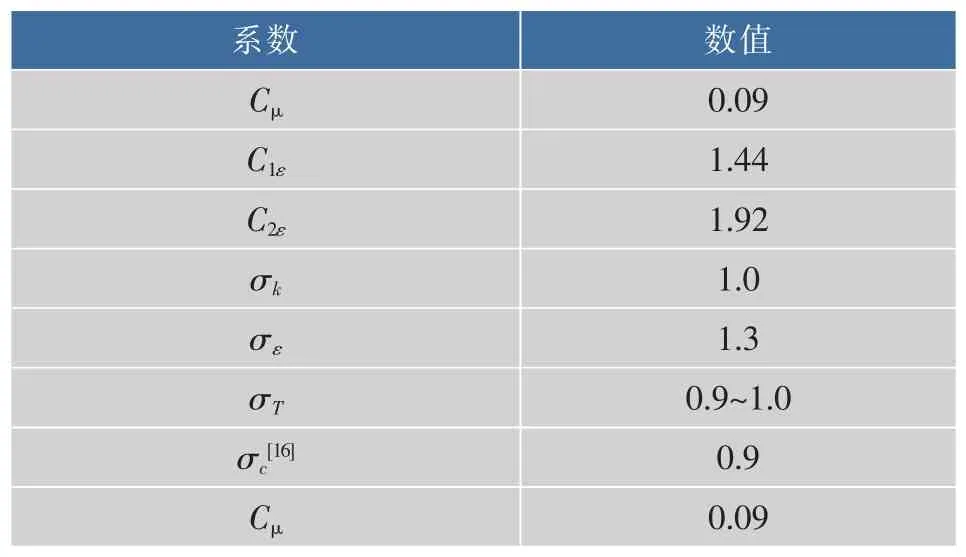
表1 k－ε模型中的参数Table 1 Coefficients of the k－ε model

2.3 货物区数学模型的建立

气调库内货物堆放方式与普通冷藏库不同，通常采用高堆满放方式，这样使库内气体所占容积相对较小，有助于缩短降氧时间。针对货物的特点，将苹果视为球形固体颗粒，苹果间存在间隙，因此将货物区视为多孔介质处理。

2.3.1 动量方程 由于货物箱壁的阻碍以及货物区多孔结构造成极大的流动阻力，货物区中的气体流动极其微弱，对气调库内主流区的影响可以忽略，因此对货物区中气体流速进行修正为u=v=w=0。

2.3.2 能量方程 本文研究的苹果堆满足文献[17]中多孔介质的假设，因此货物区的能量传递控制方程为：

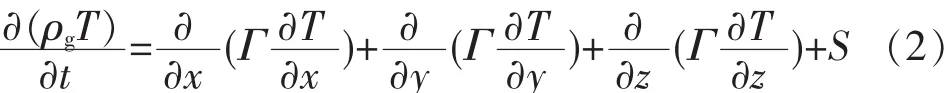
式中，Γ为热扩散系数，S为果蔬呼吸引起的源项，计算公式如下：

式（3）中：

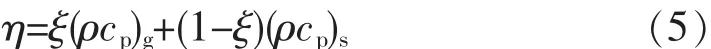
式（3）～（5）中，下标 g 和 s分别代表气体、固体；Qr为呼吸热，W/kg，ξ为多孔介质的孔隙率，可以取为 ξ=0.35[16]，λe为货物区的当量导热系数。Qr数值是由呼吸强度的大小确定。呼吸强度是指单位质量的果蔬在单位时间内释放出的二氧化碳摩尔数或者吸收的氧气摩尔数，用WCO2或WO2表示，单位为mol/(kg·h)。在贮藏过程中，果蔬的呼吸强度是贮藏温度T、贮藏环境中氧气和二氧化碳组分浓度的函数。在本研究中，苹果进入气调库时已经进行预冷处理，温度为苹果适宜的贮藏温度0℃。根据文献[18]，经过实验数据回归后得到的苹果呼吸强度计算公式（当时t=0℃）如下：

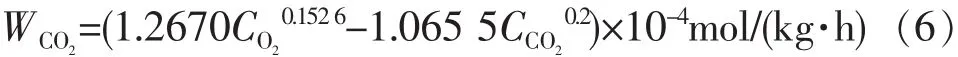
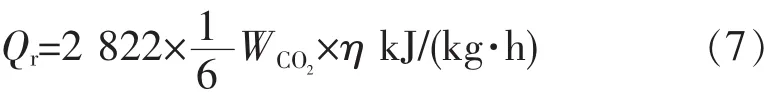
式中η表示呼吸能量转换成热量的转换系数，一般认为呼吸能量转换为热量的部分约为55%[19]。

2.3.3 气体组分浓度方程 货物区的气体组分浓度方程可以用以下控制方程描述：

根据果蔬有氧呼吸原理，则呼吸作用产生的呼吸热为：

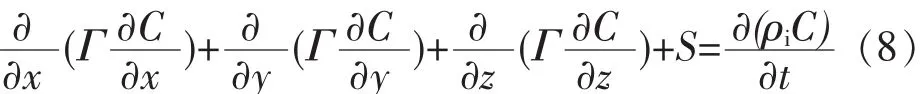
式中Γ为多孔介质中的质量扩散系数，S为果蔬的呼吸作用所引起的源项。

果蔬呼吸作用消耗氧气产生二氧化碳，这样就导致了氧气组分浓度方程和二氧化碳组分浓度方程源项的产生。根据文献[18]，苹果在健康呼吸条件下，吸收的氧气摩尔数和释放的二氧化碳摩尔数比值是十分接近于1的。因此，根据式子（6）确定氧气组分浓度方程的源项SO2：

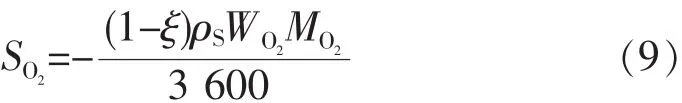
式子（9）中，ρS为苹果密度，取 790 kg/m3；WO2为氧气的摩尔质量，为0.032 kg/mol，MO2为二氧化碳的摩尔质量，为 0.044 kg/mol。

2.4 边界条件的设定

将冷风机送风口和氮气进口均设置为速度入口，参数设置根据冷风机型号和制氮机型号以及氮气管径确定，出口边界均设置为 outflow。壁面采用无滑移边界，温度按第三类边界条件处理，各气体组分在壁面无通量。

2.5 UDF程序功能

编译的UDF程序主要包含两个方面：一是冷风机送风口边界的各气体组分的质量分数赋值，二是货物区的氧气、二氧化碳组分方程的源项以及能量方程的源项。

冷风机送风口边界赋值UDF程序的功能为：每次计算时将冷风机回风口边界各组分的平均质量分数计算后赋值给冷风机送风口边界。这种处理方法是因为：充氮降氧阶段气调库内的氧气、二氧化碳和氮气组分的体积分数是时刻变化的，而库内气体通过冷风机进行强制对流时，经过冷风机的各组分质量分数并不会改变，因此该UDF程序的处理方法符合冷风机处真实的传质情况。该UDF程序为循环流动问题中入口边界条件的确定提供了一种解决方法。

货物区的源项UDF程序主要是描述苹果呼吸强度的变化引起的货物区气体组分浓度方程和能量方程源项的变化。充氮降氧阶段库内的O2和CO2体积分数是时刻变化的，而苹果的呼吸强度随着周围环境中O2和CO2体积分数变化而改变，这样就导致了苹果吸收的O2量、释放的CO2量以及产生的呼吸热都在时刻变化。根据文献[18]的苹果呼吸强度拟合公式编写的货物区源项UDF程序可以真实的描述苹果在气体调节过程中的生理活动对周围环境的影响。

3 结果与分析

3.1 充氮降氧过程氧气体积分数计算值与实验值对比

苹果的最佳气调贮藏参数为O2体积分数3%，而文献[20]指出库内O2体积分数降至比规定值高出2～3个百分点时，即可停止降氧。作者对一实际气调库的降氧过程进行了数值计算，其制氮机工作参数是制氮量为30 m3/h，氮气纯度为95%。库内气体组分测点坐标为X=3.2 m，Y=0.4 m，Z=5.0 m，为了进行对比，在计算过程中在货物区中心位置设置测点坐标为X=2.3 m，Y=4.5 m，Z=2.85 m。为了验证气调库内气体流动与传热传质数学模型及数值计算结果的正确性和可靠性，作者以相关文献[15]的实验数据进行验证，得到了充氮降氧阶段库内气体组分浓度测点处的氧组分浓度计算值与实验值的对比，结果见图2。计算值与实验值的相对偏差最大值为0.068，最小值为0.005 6，平均值为0.027，数值计算结果与实验值有较好的一致性。

3.2 充氮降氧过程结束时O2体积分数分布规律

图3为充氮降氧阶段结束后，x=2.3 m截面O2体积分数场分布。图中可以看出气体区的O2的组分由于风机的强制对流作用使其分布比较均匀，货物区O2体积分数分布则呈现出明显的梯度，这是由于货物区的O2体积分数变化主要是由于扩散作用，根据文献[21]高体积分数侧与低体积分数侧的组分在空间上的分布是均匀递减的，从而导致了这种体积分数分层现象。

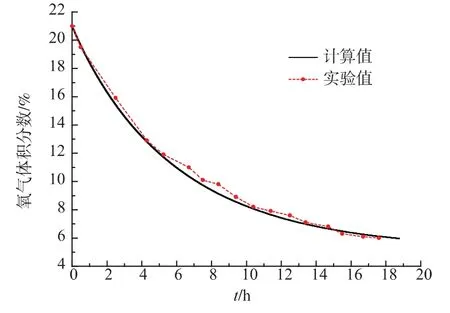
图2 气调库内测点处氧气体积分数变化计算值与实验值的对比Fig.2 Comparison of simulated values and experimental values of oxygen specie concentration at measuring point

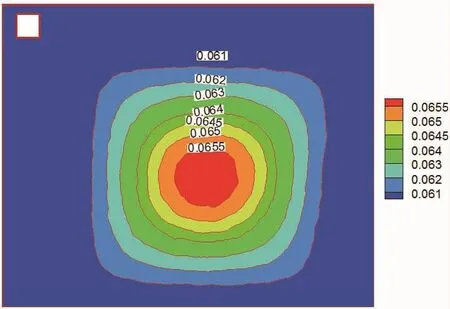
图3 x=2.3 m截面O2组分浓度分布Fig.3 Distribution of O2specie concentration at the plane of x=2.3 m

通过上述分析可知：果蔬气调库内氧气体积分数受制氮机工作参数和果蔬呼吸作用的综合影响，并且库内氧气分布并不均匀，因此难以通过简单的数学计算获得准确的降氧时间，运用CFD软件建立三维数值计算模型进行求解是必要且可行的。

3.3 氮气纯度对降氧时间的影响

由于降低库内氧气浓度是通过向库内充入高纯度氮气实现的，那么氮气纯度就会影响降氧速度。

对于任何已经选定型号的制氮机或制氮系统，其流量和纯度是呈反比的，即提高氮气纯度则氮气流量会下降。本研究中制氮机工作参数见表2。

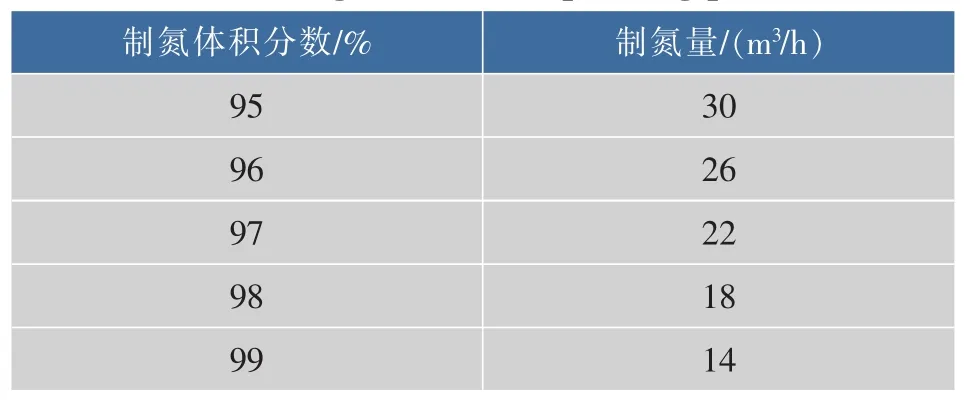
表2 制氮机工作参数Table 2 Nitrogen machine operating parameters

图4为不同氮气纯度下得到的气体区测点位置的降氧曲线。可以看出，不同的氮气纯度对应着最快的降氧区间，当氧气体积分数从21%降至8.8%之间任意一点时，95%纯度的氮气所需时间最短；而降至8.8%～6%之间任意一点时，96%纯度的氮气所需时间最短；而降至6%～4.4%之间任意一点时，97%纯度的氮气所需时间最短；而降至4.4%～2.9%之间任意一点时，98%纯度的氮气所需时间最短；而降至2.9%～1%之间任意一点时，99%纯度的氮气所需时间最短。

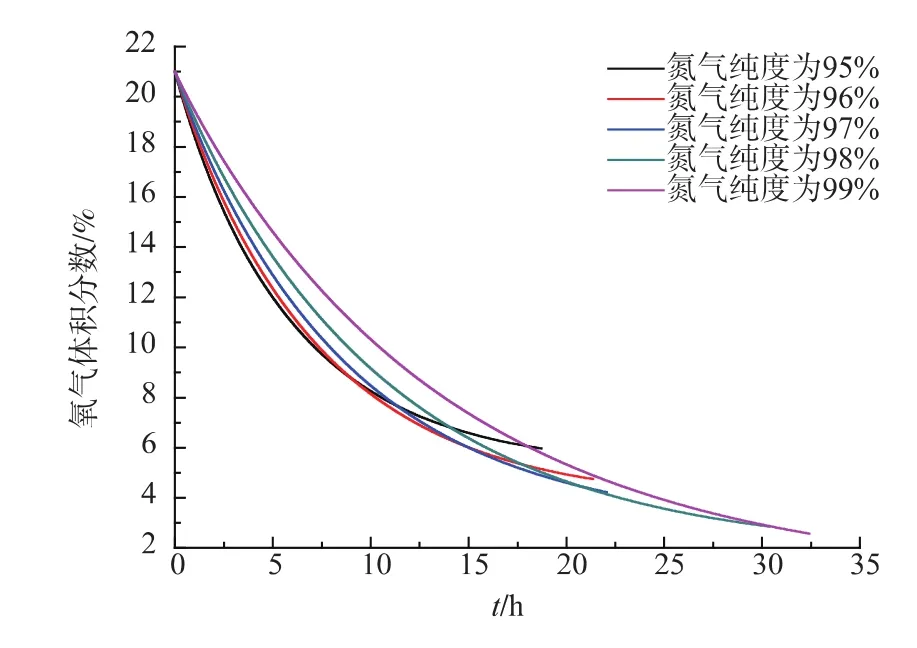
图4 不同氮气纯度充注情况的O2体积分数变化Fig.4 Changing value of O2concentration of different purity nitrogen filled cases

3.4 不同种类果蔬对降氧时间的影响

不同种类或品种的果蔬呼吸强度相差很大，呼吸强度影响着果蔬的生理变化，同样也影响着贮藏环境的变化。作者在已有的果蔬呼吸强度相关研究基础上，选择了与苹果贮藏指标接近但呼吸强度却相差较大的黄桃作为对比，研究了苹果和黄桃的呼吸作用对充氮降氧过程中降氧时间的影响，其中黄桃呼吸速率拟合公式由文献[16]得到。

图5为贮藏货物分别为黄桃和苹果时，库内气体区测点位置的氧气浓度变化对比。货物堆体积相同，采用纯度为96%、流量为26 m3/h的氮气充入。

根据相关研究的成果分别计算苹果和黄桃的呼吸速率，得到温度为0℃时，处于空气中黄桃的呼吸速率为 11.8 mL/（kg·h）， 苹果为 1.77 mL/（kg·h），3%氧气、3%二氧化碳的气体条件下黄桃的呼吸速率 6.4 mL/（kg·h），苹果为 0.65 mL/（kg·h）。 根据计算结果可以看出，黄桃在同样贮藏条件下呼吸速率是远大于苹果的。从图4可以看出，在同样的氮气纯度和流量下，由于黄桃的呼吸强度比苹果大，降氧时间有明显缩短，苹果需要15 h，黄桃只需要11.5 h。由于呼吸强度大的果蔬氧气消耗速度和二氧化碳生成速度都较快，因此制氮设备和二氧化碳洗涤装置进行选型时，应该根据果蔬呼吸强度的大小匹配合适的型号。

图5 同样条件下黄桃和苹果的降氧时间对比Fig.5 Comparison of the reducing oxygen time of peaches and apples under the same conditions

4 结语

作者以西安某苹果气调库为研究对象，建立了气调库内气体流动、传热与传质的三维耦合数学求解模型，对气调库的快速降氧过程进行了数值计算，并对数学模型及数值计算结果的正确性、可靠性进行了验证。经过验证，本研究得到的数值计算结果与实验值有较好的一致性，因此建立的数学模型可以较真实地反映气调库内氧气组分浓度的变化情况。

不同的氮气纯度对应着不同的最快降氧区间，对于苹果气调而言，制氮机的制氮纯度为96%时可以在最短时间内把氧气体积分数降至6%，不仅可以使果蔬快速进入气调效果，还可以节约降氧动力的消耗。呼吸强度差别较大的果蔬降氧时间有明显差异，根据果蔬呼吸强度的大小匹配合适型号的制氮设备和二氧化碳洗涤装置不仅可以使果蔬达到更好的贮藏效果，还可以使设备投资更加合理。本研究对于获取实际气调库降氧时间及选择合理的制氮机、改进气调工艺具有重要参考价值。

[1]ZHAO Changqing，FU Zetian，LIU Xue，et al.Temperature monitoring and warming system in cool food chain transportation[J].Microcomputer Information，2010，26（6）：27-28.（in Chinese）

[2]DELELE M A，SCHENK A，RAMON H，et al.Evaluation of a chicory root cold store humidification system using computational fluid dynamics[J].Journal of Food Engineering，2009，94（1）：110-121.

[3]PAULL R.Effect of temperature and relative humidity on fresh commodity quality[J].Postharvest Biology and Technology，1999，15（3）：263-277.

[4]LOPEZ A，PIQUE M，ROMERO A，et al.Influence of cold-storage conditions on the quality of unshelled walnuts[J].International Journal of Refrigeration，1995，18（8）：544-549.

[5]TASHTOUSH B.Natural losses from vegetable and fruit products in cold storage[J].Food Control，2000，11（6）：465-470.

[6]DEVRES Y，BISHOP C.Computer model for weight loss and energy conservation in a fresh-produce refrigerated store[J].Applied Energy，1995，50（2）：97-117.

[7]CHOURASIA M，GOSWAMI T.Steady state CFD modeling of airflow，heat transfer and moisture loss in a commercial potato cold store[J].International Journal of Refrigeration，2007，30（4）：672-689.

[8]CHOURASIA M，GOSWAMI T.Simulation of effect of stack dimensions and stacking arrangement on cool-down characteristics of potato in a cold store by computational fluid dynamics[J].Biosystems Engineering，2007，96（4）：503-515.

[9]JI Amin.Numerical simulation and experimental Verification of temperature Variation tluring controlled atomospherecold storage offruitsandVegetables[J].Transactions of the Chinese Society of Agricultural Engineering，2006，22（5）：24-27.（inChinese）

[10]WANG Yizhong，HU Chunyuan，CHEN Shaohui，et al.Study on numerical simulation of temperature and humidity fields in a refrigerated vehicle[J].Storage and Process，2010，10（3）：26-29.（in Chinese）

[11]LIU Bin，YANG Zhao，LI Xihong，et al.Experiment on air disrtibution and storage effects in mini-cold storage[J].Journal of Tianjin University，2005，38（10）：897-900.（in Chinese）

[12]李敏华.气调库制氮系统的改进设计及其气流组织的数值模拟[D].广州：华南理工大学，2004.

[13]瞿晓华.果蔬气调库的气体流场分析及优化设计[D].上海：上海水产大学，2004.

[14]李勇祁.装配式气调库浓度分布及CAD研究[D].上海：上海水产大学，2001.

[15]HU Hao，YUAN Xiuling，SUN Dawei，et al.Three dimensional dynamic simulation and experiment investigation about temperature and oxygen density variationprocess of the fruit CA storage[J].Journal of Refrigeration，2009，94：110-122.（in Chinese）

[16]刘颖.果蔬快速降氧气调贮藏环境的热动力学研究[D].上海：上海交通大学，2004.

[17]林瑞泰.多孔介质传热传质引论[M].北京：科学出版社，1995.

[18]LIANG Dawei，ZENG Danling，AO Yue，et al.The mathematical model of the storage of fruits and vegetables by adjusting the atmosphere inside the system[J].Journal of Engineering Thermophysics，1990，11（1）：5-8.（in Chinese）

[19]赵家禄，黄清华.小型果蔬气调库[M].北京：科学出版社，2000.

[20]张祉祐.冷藏与空气调节[M].北京：机械工业出版社，1995.

[21]连之伟.热质交换原理与设备[M].北京：中国建筑工业出版社，2006.