p型多晶硅薄膜应变因子与掺杂浓度关系理论研究∗

王健 揣荣岩

1)(沈阳化工大学信息工程学院,沈阳 110142)2)(沈阳工业大学信息科学与工程学院,沈阳 110870)

(2017年8月7日收到;2017年9月1日收到修改稿)

1 引 言

多晶硅薄膜作为力敏电阻在半导体压力传感器上应用较多[1−8].与单晶硅比较,应用和工作温度范围广,但压阻系数小.为了提高多晶硅薄膜的性能,人们在薄膜的制备方法和压阻理论上探索研究.制备方法上主要是设计晶粒结构和掺杂浓度,压阻理论主要是求取基础压阻系数和应变因子理论公式[9−14].

多晶硅薄膜按膜厚分为普通多晶硅薄膜和多晶硅纳米薄膜两种.普通多晶硅薄膜(薄膜厚度≥0.3µm)温度特性好但压阻系数小,而多晶硅纳米薄膜(薄膜厚度≤0.1µm)不仅温度特性好,而且压阻系数高[15].

20世纪末期,提出了普通多晶硅薄膜压阻理论,并在实验和应用中得到了验证[16,17].但是,p型多晶硅纳米薄膜在掺杂浓度高于1020cm−3时,应变因子随掺杂浓度的增加而增大,而且应变因子随晶粒减小而增大[15].普通多晶硅薄膜压阻理论无法解释该现象.2006年多晶硅隧道压阻模型[15,18−20]被提出,给出了薄膜的纵向应变因子表达式,与测试数据比较一致.由于该方法计算的晶粒中性区(单晶硅)的π44比测试结果低,故采用p型单晶硅与掺杂浓度测试数据拟合曲线,而且只给出了压阻系数π44理论公式,而没有π11和π12.

在T=4 K时,p型单晶硅多数空穴在波矢k=0处且价带简并,在应力作用下,简并的重空穴和轻空穴能级分裂,导致空穴重新分布,产生压阻效应[21,22].基于该机理推导的压阻系数π44在重掺杂时比测试结果低,原因是在典型压力传感器的工作条件(温度:73–373 K,压力＜100 MPa)下,多数空穴不在k=0处,且能带没有完全去简并[23].在2002年,Toriyama和Sugiyama[23]提出了一种近似的价带方程,基于该方程,在典型压力传感器工作条件,应力作用下,空穴在价带中分布和电导质量改变,产生压阻效应.基于该机理计算的压阻系数π44与掺杂浓度关系曲线与测试结果一致性好.

本文基于多晶硅隧道压阻模型,依据Toriyama和Sugiyama[23]提出的p型单晶硅压阻效应机理,建立了一种p型多晶硅薄膜压阻系数算法,给出了基础压阻系数π11,π12和π44,并依此求取择优晶向排列的多晶硅应变因子.

2 理 论

多晶硅是由许多小晶粒构成,图1为p型多晶硅结构图.晶粒中性区是一块单晶体,各自具有不同的晶向,连接各个小单晶体颗粒的为晶粒边际(边界),它的原子呈无序排列,其厚度通常有几个原子层[15].w是耗尽区宽度,L是晶粒长度,δ是晶粒边界宽度.

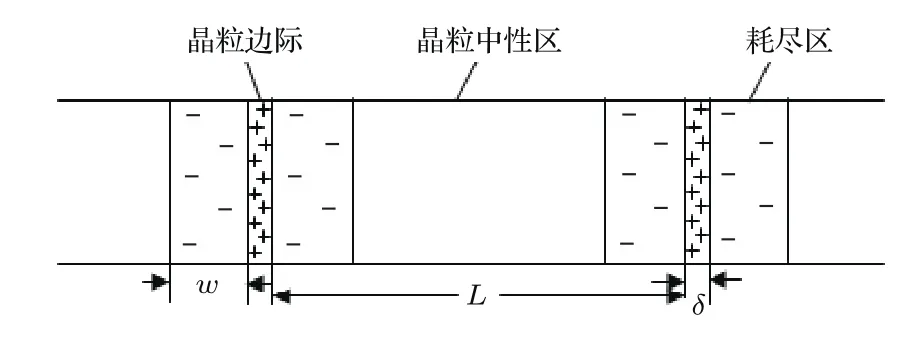
图1 p型多晶硅结构[15]Fig.1.p-type polysilicon structure[15].

多晶硅隧道压阻模型认为应力的作用使价带顶简并能带分裂,各能带空穴浓度改变,导致晶粒中性区的电导率、耗尽区(势垒区)的热发射载流子电流和晶粒边界(晶界)隧道电流改变,产生压阻效应[15,18−20].

在一般工作温度下,多晶硅应变因子Gp的表达式为[15]

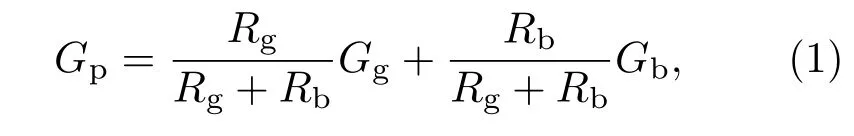
式中,Rb为复合晶界电阻,Rb=Rd+Rδ,其中Rd是热发射电流决定的发射电阻,Rδ是隧道电流决定的隧道电阻;Rg是晶粒中性区的电阻;Gg和Gb为Rb和Rg的应变因子,分别由对应区的压阻系数和弹性参数决定.

该模型只考虑应力作用下价带中空穴浓度的变化,忽略了电导质量的改变,导致计算的π44与测试数据偏差大.为此,本文采用Toriyama和Sugiyama[23]给出的p型硅价带能级和电导质量与应力的关系表(下面简记为关系表),对p型多晶硅纳米薄膜的压阻系数进行推导,并应用于普通多晶硅薄膜.

2.1 晶粒中性区压阻系数

p型多晶硅薄膜每个晶粒中性区是由一定晶向的单晶硅构成,因此,晶粒中性区压阻系数就是p型单晶硅的压阻系数[15].

由于Toriyama和Sugiyama[23]没有给出完整压阻系数理论公式,本文给出p型单晶硅压阻系数.

空穴电导率σ表达式为[23]

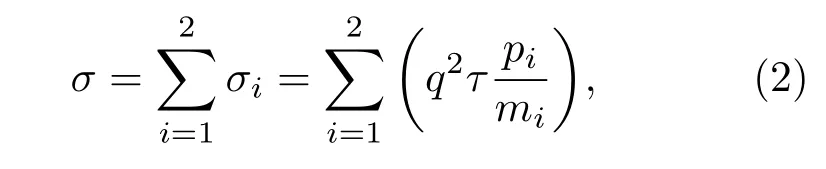
式中,τ为弛豫时间;mi为空穴电导质量;i=1,2分别对应重空穴和轻空穴;pi为空穴浓度;q为单位电荷电量.

空穴浓度pi表达式为

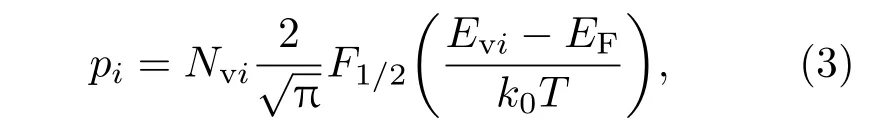
式中,Nvi为价带的有效状态密度,Fj[(Evi−EF)/(k0T)]为j阶费米积分,k0是玻尔兹曼常数,T为绝对温度,Evi是价带顶能量,EF是费米能级.

假设弛豫时间τ各向同性且不随应力作用而变化,并受自旋-轨道耦合能带影响很小,则应力X作用下,p型单晶硅压阻系数πg为[23]

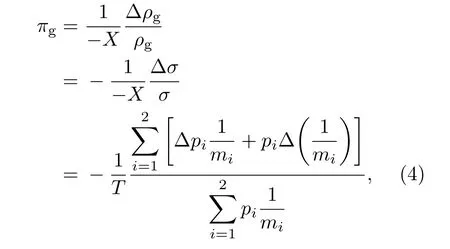
式中,πg为晶粒中性区电阻率,Δ为应力作用下参数变化量.

将关系表[23]代入(4)式中,得到在X‖[001]且J‖[001],X‖[001]且J‖[010]和X‖[110]且J‖[110]三种情况下的压阻系数πl[001],πt[001]和πl[110].这里,X是应力,J为电流密度.

根据

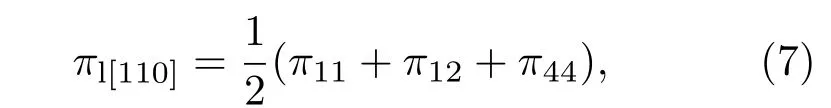
得晶粒中性区基础压阻系数πg11,πg12和πg44分别为

式中,π11,π12和π44为基础压阻系数.

从(3)式计算不同掺杂浓度下的费米积分,代入(8),(9)和(10)式可得掺杂浓度与压阻系数关系曲线.

2.2 晶界势垒区的压阻系数

当晶界势垒区和晶粒中性区受到应力作用时,晶粒中性区价带顶不再简并,重空穴和轻空穴能带中空穴重新分布,而且空穴电导质量也变化,因此改变了晶界势垒区的热发射电流.

设Vgb是晶界上的偏压,VL和VR分别为晶界左侧和右侧势垒区上的偏压,则外加电压V0的表达式为[15]

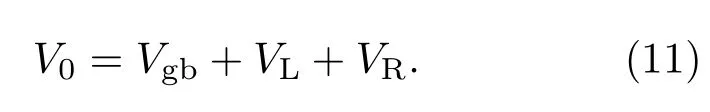
在外电压V0作用下势垒区热发射电流Jd的表达式为[15]

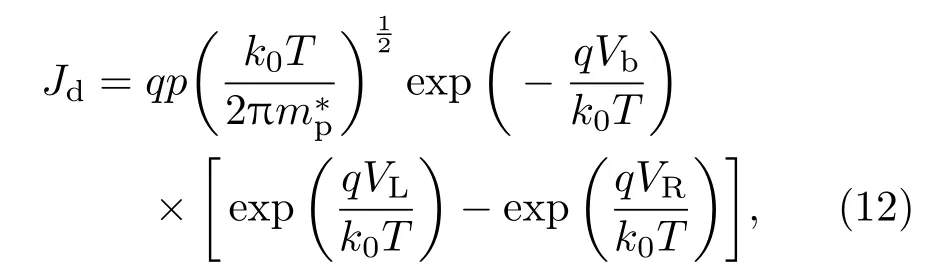
式中,Vb为势垒电势,为空穴有效质量.

为了等效价带中能带相互作用,将(12)式的空穴浓度表达式中有效质量设为状态密度有效质量,其他有效质量设为电导质量,则重空穴热发射电流密度Jd1表达式为

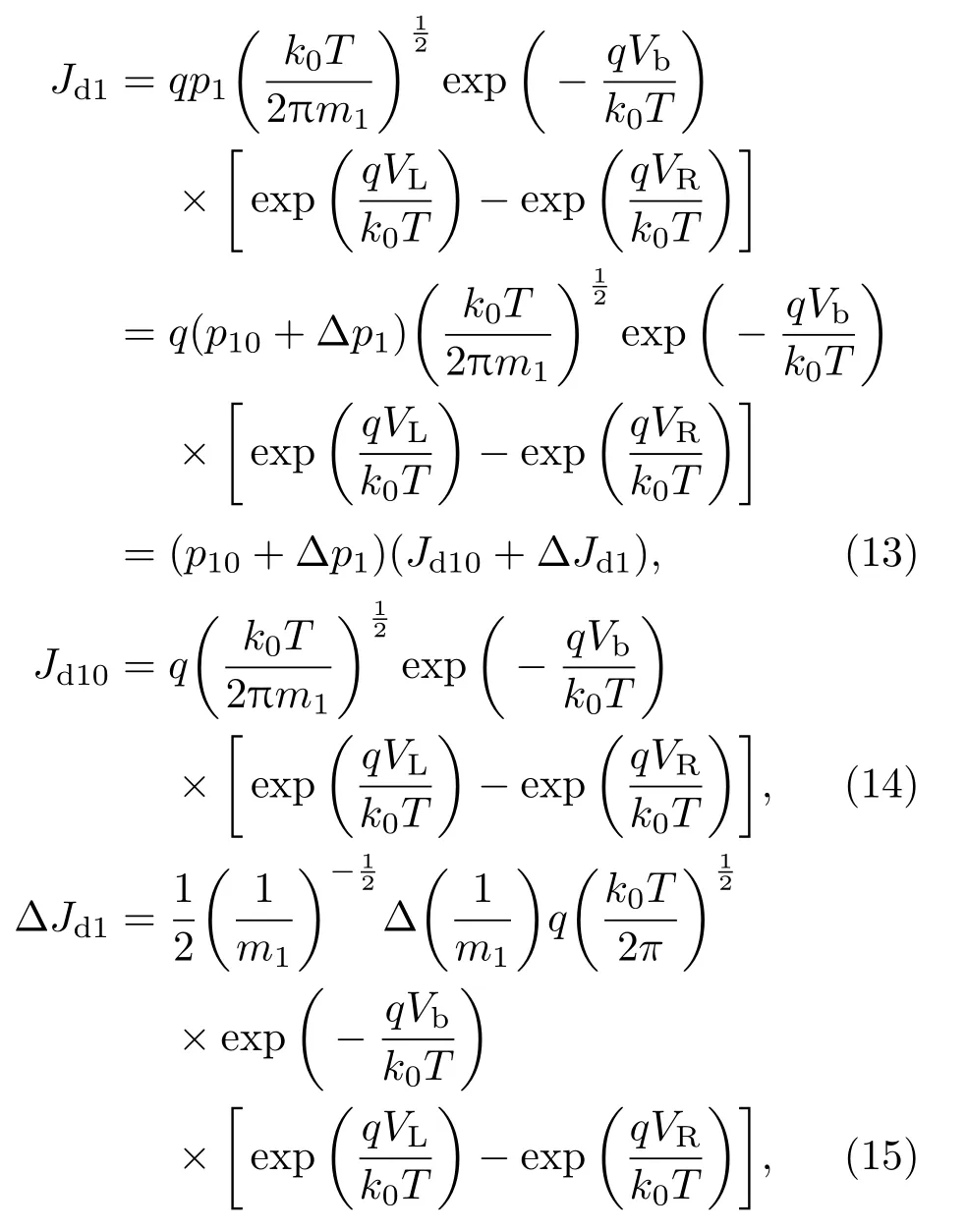
式中,p10为无应力时重空穴浓度,Δp1为有应力时重空穴浓度改变量,Jd10为势垒区无应力时一个重空穴热发射电流密度,ΔJd1为势垒区有应力时一个重空穴热发射电流密度改变量.

同理,可以求得轻空穴热发射电流密度Jd2.

由欧姆定律,晶界势垒区电阻率ρd的表达式为[15]

晶界势垒区压阻系数πd为

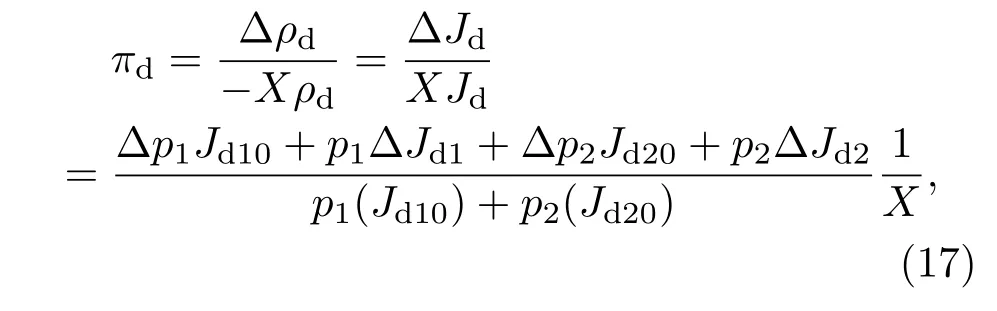
式中,Δp2为有应力时轻空穴浓度改变量,Jd20为无应力时一个轻空穴热发射电流密度,ΔJd2为有应力时一个轻空穴热发射电流密度改变量.

采用晶粒中性区相同方法得到晶界势垒区基础压阻系数πd11,πd12和πd44的表达式为

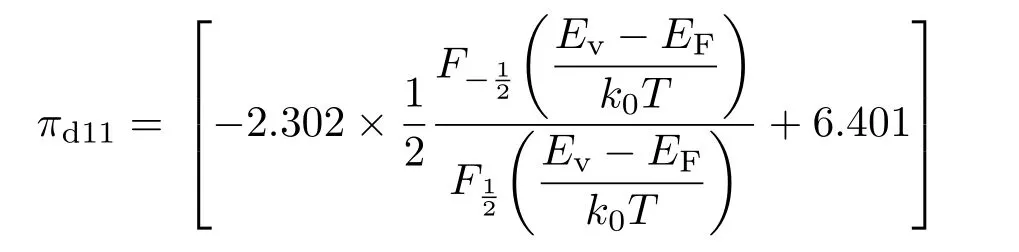
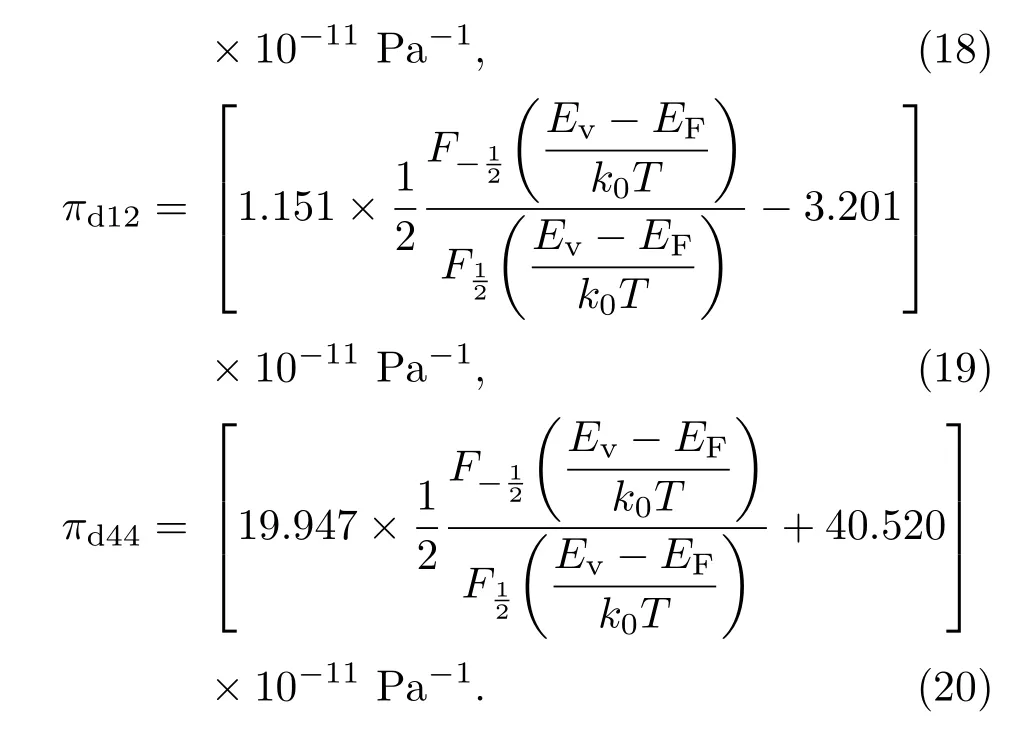
2.3 等效隧道电阻的压阻系数

为了等效价带中能带相互作用,有效质量设置同2.2节.应力作用下,能带改变使空穴浓度重新分布,并且电导质量的改变也使空穴的电流密度改变,则总隧道电流密度Jδ和一个空穴隧道电流密度Jδ0分别为

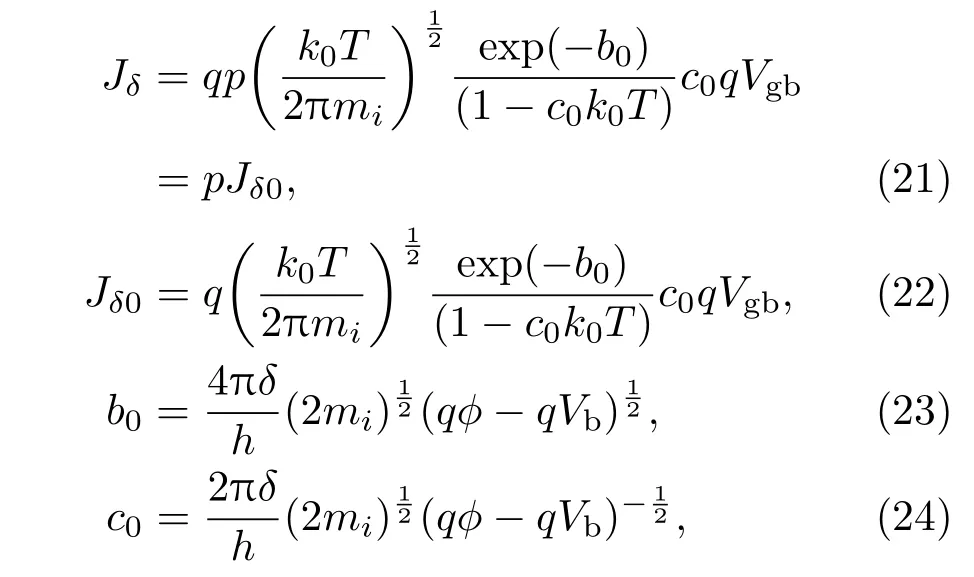
式中,ϕ是晶粒边界势垒高度.

实际上Jδ是由价带顶的两个简并能带中的空穴形成的,重空穴和轻空穴能带的隧道电流密度分别用J1δ和J2δ表示,则隧道压阻系数πδ的表达式为

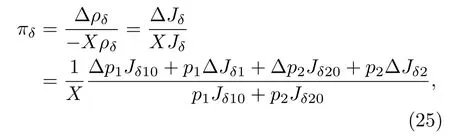
式中,ρδ为晶粒边界区电阻率,Jδ10和Jδ20为晶粒边界区无应力时一个重空穴和轻空穴隧道电流密度,ΔJδ1和ΔJδ2为有应力时一个重空穴和轻空穴隧道电流密度改变量.

采用晶粒中性区相同的计算方法得晶粒边界区等效隧道基础电阻压阻系数πδ11,πδ12和πδ44为

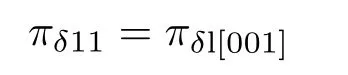
2.4 复合晶界的压阻系数

多晶硅的复合晶界是晶粒边界与其两侧势垒区共同构成的区域.通常其压阻特性由等效发射电阻和等效隧道电阻共同决定.复合晶界的压阻系数πb的表达式为[15]

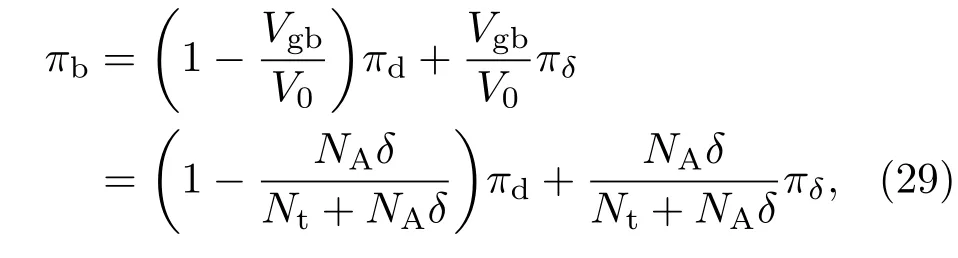
式中,NA是掺杂浓度,Nt是晶粒边界陷阱密度.

多晶硅薄膜的应变因子可表示为[15]

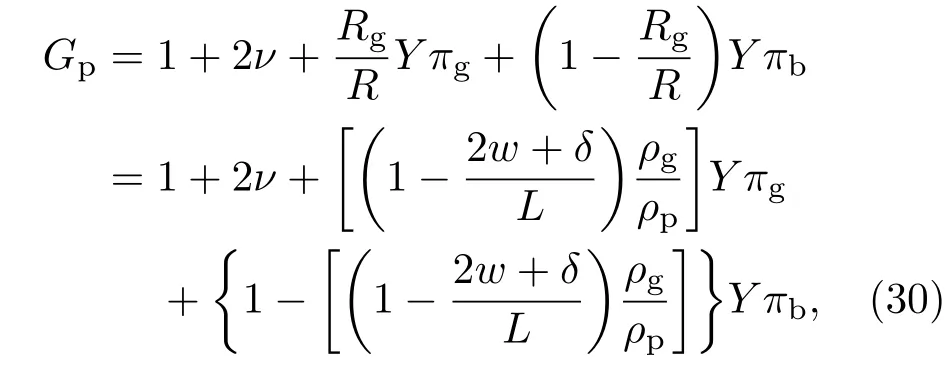
式中,Y为弹性膜片的杨氏弹性模量,ν为弹性膜片的泊松比,ρg为单晶硅电阻率,ρp为多晶硅电阻率.

3 结果与讨论

3.1 多晶硅纳米薄膜应变因子

多晶硅应变因子测量通常为悬臂梁和压力传感器两种方法[15,24,25],本文采用悬臂梁法[15].根据多晶硅纳米薄膜测试结果,取晶粒度L=30 nm,多晶硅薄膜的晶粒取向呈随机分布状态.晶粒边界势垒宽度δ=1 nm,qϕ−qVb=0.66 eV,晶界陷阱密度Nt=1013cm−2[15],取泊松比ν=0.062和杨氏弹性模量Y=1.69×1011Pa,对于80 nm厚的多晶硅纳米薄膜,给出室温时多晶硅电阻率ρp与掺杂浓度的关系为[15]

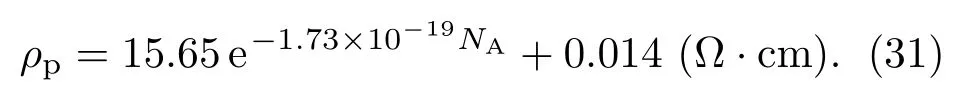
根据p型单晶硅电阻率与掺杂浓度关系曲线[26],给出室温下单晶硅电阻率ρg与掺杂浓度关系为

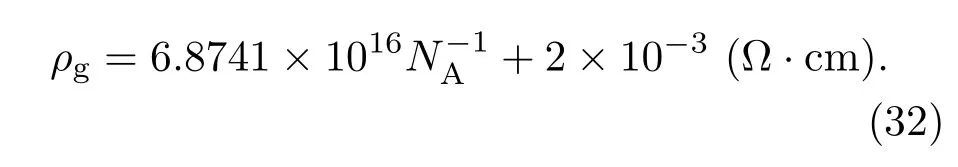
由于膜厚小于100 nm的多晶硅薄膜的晶粒取向呈随机分布状态,纵向和横向压阻系数为[27]

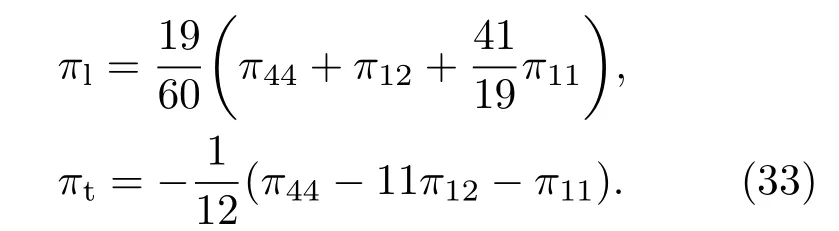
将晶粒中性区和复合晶界区压阻系数代入(33)式得到纵向和横向压阻系数,再与(31)和(32)式一起代入(30)式中,获得多晶硅纳米薄膜纵向和横向应变因子与掺杂浓度的关系式,并与测试结果比较,如图2所示.应变因子计算与测试均值的误差小于相同掺杂浓度下的测试数据的最大和最小差值的1/2,因此,测试与计算结果一致性较好.

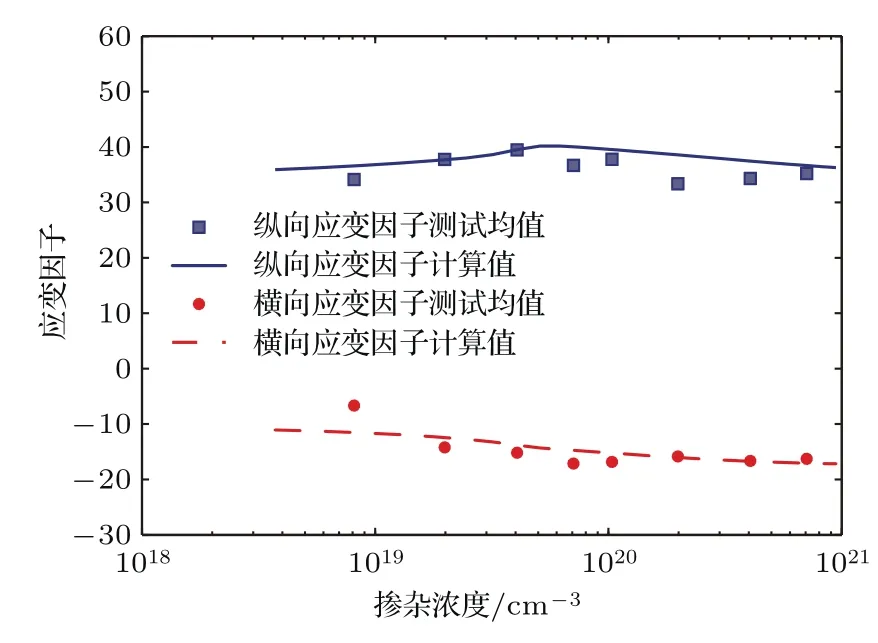
图2 多晶硅纳米薄膜应变因子与掺杂浓度关系的计算值与测试值比较Fig.2.Comparion of calculated results with experimental values of the polysilicon nano fi lm gauge factors as a function of doping concentration.

3.2 普通多晶硅薄膜应变因子

采用该算法计算普通多晶硅薄膜应变因子与掺杂浓度的关系曲线,并与French和Evans[28]测试数据对比.其中,晶粒度L=135 nm,薄膜厚度为0.4 µm,晶粒中性区取向为:〈311〉:〈111〉:〈110〉=49:31:20[28],其他参数与上述多晶硅纳米薄膜相同.普通多晶硅薄膜电阻率与浓度关系为[28]

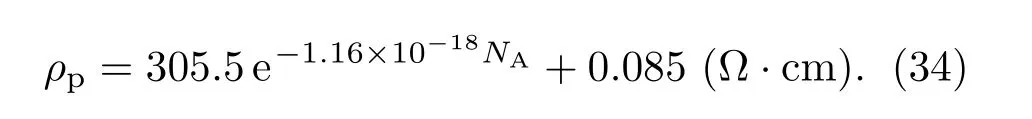
采用与多晶硅纳米薄膜相同方法,获得普通多晶硅薄膜的纵向和横向应变因子与掺杂浓度关系式,普通多晶硅薄膜应变因子的计算结果与测试结果对比如图3所示.从结果可以看出一致性很好.说明该算法也适用于普通多晶硅薄膜.

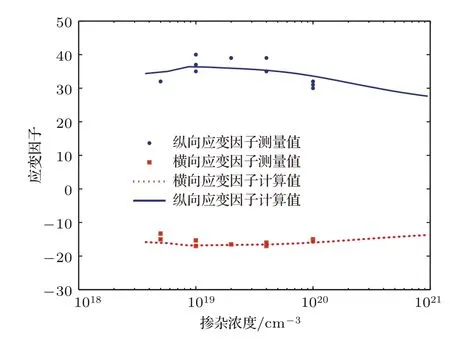
图3 普通多晶硅薄膜应变因子与掺杂浓度关系的计算值与测试值比较Fig.3.Comparison of calculated values with experimental values of the common polysilicon fi lms gauge factors as a function of doping concentration.

4 结 论

基于多晶硅隧道压阻模型,采用应力作用下p型单晶硅的价带和电导质量改变的压阻效应机理,提出了p型多晶硅薄膜压阻系数算法.该算法给出了基础压阻系数π11,π12和π44的表达式,从而可以依此求取任意比例晶向排列的多晶硅压阻系数.提出了p型多晶硅薄膜的横向和纵向应变因子的理论公式.

本文给出了p型多晶硅纳米薄膜和普通多晶硅薄膜应变因子与掺杂浓度理论曲线,与测试数据对比,计算与测试结果一致性较好,表明本文提出的压阻系数算法合理地解释了p型多晶硅纳米薄膜和普通多晶硅薄膜压阻特性.

[1]Niu D F,Wen W P,Ma L Z 1994Inst.Tech.Sens.6 13(in Chinese)[牛德芳,闫卫平,马灵芝1994仪表技术与传感器6 13]

[2]Zhang W X,Mao G R,Yao S Y,Qu H W 1996J.Tianjin Univ.29 466(in Chinese)[张维新,毛赣如,姚素英,曲宏伟1996天津大学学报29 466]

[3]Mao G R,Yao S Y,Qu H W,Li Y S 1997J.Tianjin Univ.30 767(in Chinese)[毛赣如,姚素英,曲宏伟,李永生1997天津大学学报30 767]

[4]Zao X F,Wen D Z 2008Chin.J.Semicond.29 45(in Chinese)[赵晓锋,温殿忠 2008半导体学报 29 45]

[5]Zhang D Z,Hu G Q,Chen C W 2009Inst.Tech.Sens.11 55(in Chinese)[张冬至,胡国清,陈昌伟 2009仪表技术与传感器11 55]

[6]Wang J,Chuai R Y,Yang L J,Dai Q 2015Sens.Actuators A:Phys.228 75

[7]Chuai R Y,Wang J,Yi C,Dai Q,Yang L J 2015IEEE Sens.J.15 1414

[8]Wu Z Z,Ahn C H 201719th International Conference on Solid-State Sensors,Actuators and Microsystems(TRANSDUCERS)Kaohsiung Taiwan,China,June 18–22,2017 p256

[9]Smith C S 1954Phys.Rev.94 42

[10]Erskine J C 1983IEEE Trans.Magn.30 796

[11]French P J,Evens A G R 1984Electron.Lett.20 999

[12]Schubert D,Jenschke W,Uhlig T,Schmidt F M 1987Sens.Actuators A:Phys.11 145

[13]Gridchin V A,Lubimsky V M,Sarina M P 1995Sens.Actuators A:Phys.49 67

[14]French P J,Evens A G R 1985Sens.Actuators A:Phys.8 219

[15]Chuai R Y 2007Ph.D.Dissertation(Harbin:Harbin Institute Technology)(in Chinese)[揣荣岩 2007博士学位论文(哈尔滨:哈尔滨工业大学)]

[16]Suzuki K,Hasegawa H,Kanda Y 1984Jpn.J.Appl.Phys.23 L871

[17]Kleimann P,Semmache B,Le Berre M,Barbier D 1998Phys.Rev.B57 8966

[18]Chuai R Y,Wang J,Wu M L,Liu X W,Jin X S,Yang L J 2012Chin.J.Semicond.33 092003(in Chinese)[揣荣岩,王健,吴美乐,刘晓为,靳晓诗,杨理践 2012半导体学报33 092003]

[19]Chuai R Y,Liu X W,Huo M X,Song M H,Wang X L,Pan H Y 2006Chin.J.Semicond.27 1230(in Chinese)[揣荣岩,刘晓为,霍明学,宋明浩,王喜莲,潘慧艳2006半导体学报27 1230]

[20]Chuai R Y,Liu B,Liu X W 2010Chin.J.Semicond.31 032002(in Chinese)[揣荣岩,刘斌,刘晓为 2010半导体学报31 032002]

[21]Pikus G E,Bir G L 1974Symmetry and Strain-Induced Effects in Semiconductors(New York:John Wiley&Son,Inc.)pp110–150

[22]Ma J L,Zhang H M,Song J J,Wang G Y,Wang X Y 2011Acta Phys.Sin.60 027101(in Chinese)[马建立,张鹤鸣,宋建军,王冠宇,王晓艳2011物理学报60 027101]

[23]Toriyama T,Sugiyama S 2002J.Microelectromech.S.11 598

[24]Hong Y P,Liang T,Ge B E,Wang W,Zheng T L,Li S N,Xiong J J 2014Chin.J.Semicond.35 054009(in Chinese)[洪应平,梁庭,葛冰儿,王伟,郑庭丽,李赛男,熊继军2014半导体学报35 054009]

[25]Li S N,Liang T,Wang W,Hong Y P,Zheng T L,Xiong J J 2015Chin.J.Semicond.36 014014(in Chinese)[李赛男,梁庭,王伟,洪应平,郑庭丽,熊继军 2015半导体学报36 014014]

[26]Warner R M,Grung B L(translated by Lü C Z,Feng S W,Zhang W R)2005Semiconductor-Device Electronics(Beijing:Publishing House of Electronics Industry)p141(in Chinese)[沃纳R M,格兰B L著 (吕长志,冯士维,张万荣译)2005半导体器件电子学(北京:电子工业出版社)第141页]

[27]Shun Y C,Liu Y L,Meng Q H 2000Design and Manufacture of Pressure Sensor and its Application(Beijing:Metallurgical Industry Press)p62(in Chinese)[孙以材,刘玉岭,孟庆浩 2000压力传感器的设计制造与应用(北京:冶金工业出版社)第62页]

[28]French P J,Evans A G R 1989Solid-State Electron.32 1