任意存在总相伴 转化化归两相宜*
2018-01-17
●
(杭州第二中学,浙江 杭州 310053)
任意性和存在性问题是高考的热点题型之一,常常出现在压轴题和把关题中.由于涉及到双变量甚至多变量的运算,是学生最难掌握的考点之一,也是高中数学教学中的一个难点.任意性和存在性问题常常在函数知识点中考查,但也会在不等式、数列、立体几何、解析几何等各知识点中出现,源于课本,又高于课本,既能考查学生基础知识的掌握,又能考查学生分析问题、解决问题的能力.在新一轮的高中数学教改中,数学教学应从培养学生的四基四能向提升核心素养转移,而任意性和存在性问题的课堂教学,正是融入核心素养教学目标的优良载体,对学生的数学抽象、逻辑推理、运算能力等核心素养的培养有积极而明显的促进作用.
任意性和存在性问题常用的思想方法是转化化归、数形结合和分类讨论,常用的解题思路是参变分离法和主参函数法.在解题中,首先需要辨识题目是单一的任意性或存在性问题,还是混合的任意性和存在性问题;其次是相应的解题思路的优先顺序选择,这就需要一个多角度的针对性解题策略.
1 单一任意性或存在性问题
在单一的任意性或存在性问题中,解题的关键在于清楚二者的区别.在大多数题设中,关键词“任意”“恒成立”考查任意性问题,“存在”“有解”考查存在性问题,辨识度较高.
1.1 解题思路
任意性和存在性问题解题思路主要是参变分离法和主参函数法.
参变分离法就是通过对条件变形,使得双元变量分离在等式或不等式的两边,转化为求解单元函数的最值或值域问题.参变分离后,转化化归为如下的结论:
1)对∀x∈D,f(x)>m恒成立,等价于在区间x∈D上f(x)min>m;
2)对∀x∈D,f(x) 3)∃x0∈D使不等式f(x)>m成立,等价于在区间D上f(x)max>m; 4)∃x0∈D使不等式f(x) 主参函数法就是通过对条件变形,使得双元变量集中在等式或不等式的一边,另外一边为常数(多为0),以已知范围变量为主变量,所求范围变量为参变量,转化为求解区间上含参函数的最值或值域问题,多运用分类讨论的方法. 例1已知函数f(x)=ax+bx(其中a>0,b>0,a≠1,b≠1). ①求方程f(x)=2的根; ②若对任意的x∈R,不等式f(2x)≥mf(x)-6恒成立,求实数m的最大值. 2)略. (2016年江苏省数学高考试题第19题) 分析关键词“恒成立”的出现、含有两个变量的不等式(其中一个变量已知范围,求另一变量范围),这些特征的出现,就是一个典型的任意性问题. f(x)=2x+2-x. f(x)=2可化为(2x)2-2×2x+1=0,即 (2x-1)2=0, 解得x=0. ②解法1(参变分离法)由题意得 22x+2-2x≥m(2x+2-x)-6 恒成立.令t=2x+2-x,由于x∈R,2x>0,从而 此时t2-2≥mt-6恒成立,即 当且仅当t=2时取到等号,故m≤4,即m的最大值为4. 解法2(主参函数法)由题意得 22x+2-2x≥m(2x+2-x)-6 恒成立.令t=2x+2-x,由于x∈R,2x>0,从而 此时t2-2≥mt-6恒成立,即 t2-mt+4≥0 恒成立.令g(t)=t2-mt+4,则g(t)是关于t的二次函数,只需当t≥2时,g(t)≥0恒成立,根据二次函数g(t)的图像,可得 或 解得m≤4,故m的最大值为4. 评注参变分离法与主参函数法在大多数题中都可以使用,因此在解题时两者都可以尝试,具体问题具体分析,最终视解法的难易程度择优即可. 在解题策略上,“把握本质,多手准备”:1)双元变量若能分离,参变分离法是首选的方法,因为主参函数法多会涉及含参分类讨论,相对难度较大;2)双元变量在分离过程中若需要分类讨论,则需注意最后各类是取交集还是并集;3)双元变量若分离后,已知范围变量函数的最值求解难度过大,也可转而考虑主参函数法;4)双元变量若不能分离,则只能选择主参函数法. 例21)当x∈R时,x2+mx-m2+5≥0恒成立,求实数m的取值范围. 2)当x∈[-2,2]时,x2+mx+1≥0恒成立,求实数m的取值范围. 3)当m∈[-3,3]时,x2+mx+2≥0恒成立,求实数x的取值范围. 1)解设f(x)=x2+mx-m2+5,则由二次函数的图像可知,只需判别式Δ≤0即可,即 m2-4(-m2+5)≤0, 解得-2≤m≤2. 2)解条件x2+mx+1≥0可变形为 mx≥-1-x2, 要分离变量,需分类讨论: ①当x=0时,0≥-1恒成立,故此时的m∈R. 综上所述,当x∈[-2,2]时,x2+mx+1≥0恒成立,则需取三者的交集,即-2≤m≤2. 3)解法1(参变分离法)条件x2+mx+2≥0可变形为 mx≥-2-x2, 需分类讨论: ①当x=0时,0≥-2恒成立,故满足题意. 解不等式得x≤1或x≥2,即0 解不等式得x≤-2或x≥-1,即x≤-2或-1≤x<0. 综上所述,当m∈[-3,3]时,x2+mx+2≥0恒成立,则需取三者的并集,即x≤-2或-1≤x≤1或x≥2. 解法2(主参函数法)设g(m)=xm+x2+2,其中m∈[-3,3],则g(m)为一次函数,其函数图像为线段.由题意可知,g(m)≥0在m∈[-3,3]上恒成立的充要条件是 解得x≤-2或-1≤x≤1或x≥2. 评注第1)小题中的变量不能分离,只能选择以已知范围的x为主元、以m为参数的主参函数法.第2)小题中变量可以分离,但需对已知范围的x进行分类讨论,最后由于恒成立需对所有分类的x成立,因此分类结果应求交集.第3)小题中参变分离法也需讨论,但由于是对求解范围中的x进行分类讨论,恒成立只需每个分类的x成立即可,因此分类结果应求并集;第3)小题中主参函数法,由于已知范围的变量是m,因此g(m)以m为函数变量、以x为参数,又g(m)的图像是线段,故只需两个端点满足题意即可.题中所给条件不同,解题策略也应择优而选. 有些不等式或等式的题设中并没有任意性和存在性的关键词提示,需要通过数学抽象和逻辑推理来分析、转化为任意性或存在性问题.如在区间D上证明f(x) 1)略. 2)证明:f(x)>1. (2014年全国数学高考新课标卷Ⅰ理科试题第21题) 分析这道题实际上是恒成立问题,一般优先考虑f(x)min>1,通过求导,进而得到单调区间,求得函数的最小值.而 要判断正负比较困难,即使二次求导也非常复杂,因此应考虑通过变形,拆解成两个易求最值的函数,而拆解的原则是把复杂的exlnx中的ex与lnx分离. 证明要证当x>0时,f(x)>1,即证 可化为 xexlnx+2ex-1>x, 即 xlnx>xe-x-2e-1. 分别设g(x)=xlnx,h(x)=xe-x-2e-1, 则g′(x)=lnx+1,h′(x)=e-x(1-x). 当x=1时,h′(x)=0;当x∈(0,1)时,h′(x)>0;当x∈(1,+∞)时,h′(x)<0,因此 由于g(x)min与h(x)max相等,但又不能同时取到,因此g(x)>h(x)对于x>0恒成立,即f(x)>1. 评注在单元函数的任意性问题中,若不等式f(x)>g(x)在区间x∈D上恒成立,则一般先考虑其充要条件:在区间x∈D上, F(x)=f(x)-g(x)>0, 即 F(x)min>0, 但F(x)min并不一定易于求解,因此也可以考虑其充分条件:在区间x∈D上,f(x)min>g(x)max,分别计算两个函数的最值,同时视最值计算的难易,可以考虑对f(x)>g(x)变形,重新拆分成易于求最值的两个函数. (2017年浙江省数学高考试题第17题) 等价于 而由g′(x)=0,解得x=±2,则当x∈[1,2)时,g′(x)<0,即g(x)单调递减;当x∈(2,4]时,g′(x)>0,即g(x)单调递增,从而 g(x)min=g(2)=4, g(x)max=max{g(1),g(4)}=max{5,5}=5, 于是 故 2a-5≤4, 即 f(1)=f(4)=|5-a|+a=5-a+a=5. 评注恒成立问题可转化为函数的最值问题,但其实函数的最值问题也可以转化为恒成立问题.本题的常规解法是通过分类讨论求函数在区间上的最值,显然对于很多学生来说过于复杂.我们要让学生知道,函数最值问题本质上只需同时保证一个任意性问题和一个存在性问题:1)f(x)≤m(≥m)在x∈D上恒成立;2)f(x)=m在x∈D上有解,则m就是f(x)在x∈D上的最值. 在双元变量函数问题中,若任意性和存在性问题同时出现时,由于两个变量的变化不同步,多采用分离变量,使得问题分离,进而分清两个函数的最值或值域关系是关键. 在不等式中,分离变量后,任意性和存在性混合问题可转化化归为如下的结论: 1)若∀x1∈D1,∀x2∈D2,则f(x1)≤g(x2)成立的充要条件是f(x)max≤g(x)min; 2)若∀x1∈D1,∃x2∈D2,则f(x1)≤g(x2)成立的充要条件是f(x)max≤g(x)max; 3)若∃x1∈D1,∀x2∈D2,则f(x1)≤g(x2)成立的充要条件是f(x)min≤g(x)min; 4)若∃x1∈D1,∃x2∈D2,则f(x1)≤g(x2)成立的充要条件是f(x)min≤g(x)max. 1)略. (2010年山东省数学高考理科试题第22题) 分析原题条件可转化为:f(x)在(0,2)上的最小值大于等于g(x)在[1,2]上的最小值,但由于g(x)在[1,2]上的最小值需要分类讨论,因此不妨先求出f(x)在(0,2)上的最小值,进而把问题转化为单一的存在性问题,用参变分离法更加简便. 当x∈(0,1)时,f′(x)<0,即f(x)单调递减;当x∈(1,2)时,f′(x)>0,即f(x)单调递增,因此f(x)在(0,2)上的最小值为 亦即 则 从而h(x)在x∈[1,2]上单调递减,于是 故 评注不等式任意性和存在性的混合问题,既可以按照上文结论分别求最值,也可优先解决其中一个问题,进而转化为单一的任意性或存在性问题,更加易于学生把握. 在等式中,分离变量后,任意性和存在性混合问题可转化化归为如下的结论:设{f(x1)|x1∈D1}=A,{g(x2)|x2∈D2}=B,则 1)∀x1∈D1,∀x2∈D2,f(x1)=g(x2)成立的充要条件是A=B; 2)∀x1∈D1,∃x2∈D2,f(x1)=g(x2)成立的充要条件是A⊆B; 3)∃x1∈D1,∃x2∈D2,f(x1)=g(x2)成立的充要条件是A∩B≠φ. (2009年浙江省数学高考理科试题第22题改编) 解当x>0时, q′(x)=g′(x)=2k2x+k; 当x<0时, q′(x)=f′(x)=3x2-2(k2-k+1)x+5. 若k=0,则当x>0时,q′(x)=0;当x<0时, 显然不满足题意,故k≠0. 当x>0时,q′(x)在(0,+∞)上单调递增,其值域为(k,+∞),记作A,即A=(k,+∞); 当x<0时,q(x)的图像为开口向上的抛物线,由于其对称轴 故q′(x)在(-∞,0)上单调递减,其值域为(5,+∞),记作B,即B=(5,+∞). 综上所述,对任意给定的正实数x1,存在唯一的负实数x2,使得q′(x1)=q′(x2)成立,则A⊆B,即k≥5. 评注等式任意性和存在性的混合问题,可以转化为两个函数在各自定义域下的值域包含问题,思路清晰,知识点熟悉. 任意性和存在性问题考查形式多样,对学生的数学思维能力、转化化归能力和创新思维能力要求较高,符合新教改关于培养学生数学核心素养的要求.学生只要把握其数学本质,通过合理的转化化归为函数最值、值域等函数性质问题,进而运用分类讨论、数形结合和函数方程思想,就能找到此类问题的突破口. 浙江省数学高考一直以来都有“重思维,重本质”的特点,而任意性和存在性问题的解题策略强调重视思维过程,重视数学本质,符合文理合卷后的新教改精神,有助于提升学生的数学核心素养,值得我们在教学中重点研究和关注.
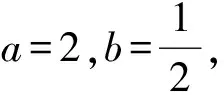
1.2 解题策略




1.3 可转化任意性和存在性的问题







2 任意性和存在性混合问题
2.1 转化为独立的最值问题





2.2 转化为值域包含问题