汲取 应用 启示*——对一道教师竞赛题的探究

●

(东庐初级中学,江苏 南京 211200)

近期，笔者有幸参加了江苏省南京市第九届优秀青年教师的笔试，遇到一道几何证明题.由于试卷容量大、试题难度大，即使教师解答出此题，限于时间的原因，无法发现此题蕴含的价值．笔试后笔者发现其实此题所蕴含的解题方法，正符合波利亚的解题步骤．波利亚的解题步骤是：1)理解题目;2)拟定方案;3)执行方案;4)回顾[1]．在这4个步骤中，“理解题目”是解题的前提；“拟定方案”是解题的关键，往往是在不断深入理解题目中进行的；“执行方案”是解题的具体操作呈现，较前两个步骤容易一些；“回顾”是解题的必要步骤，检查结果的同时，更应关注解题的回顾、提炼与拓展[2]．汲取波利亚的解题方法，下面我们来看看波利亚的解题方法在解题时的应用．

1 试题呈现

题目证明：对角线互相垂直的圆内接四边形的对边平方和是一个定值．

2 试题解法

2.1 理解题目

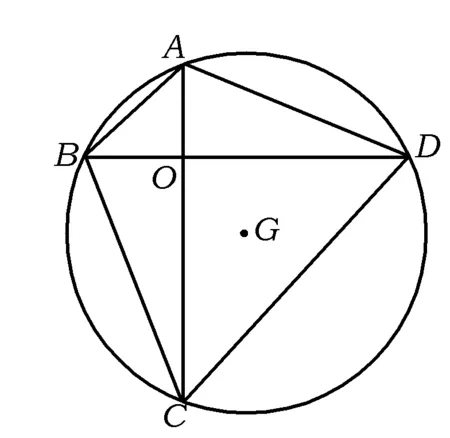
图1

理解题目是指首先要弄清题目中的已知量是什么、未知量是什么.对于文字命题的证明，首先要根据题意，画出图形(如图1)，然后结合图形写出已知、求证以及它们分别对应的已知量、未知量．已知：在⊙G中，四边形ABCD为圆内接四边形，AC⊥BD．求证：

AB2+CD2=BC2+AD2．此时题目审清了吗？答案是否定的，因为原命题的结论要求的是一个定值，AB2+CD2=BC2+AD2会等于怎样的定值？这是一个难点，笔者想到和圆有关的定值，无外乎圆的直径(不妨设为d)或者圆的半径(不妨设为r)，而AB2+CD2与BC2+AD2均是以平方的形式存在的，故笔者猜想

AB2+CD2=BC2+AD2=d2.

而d=2r，因此也可证明

AB2+CD2=BC2+AD2=4r2，

因此已知、求证可以完善为：

已知：在⊙G中，四边形ABCD为圆内接四边形，AC⊥BD，设圆的直径为d．求证：AB2+CD2=BC2+AD2=d2．

2.2 拟定方案

拟定方案就是分析问题的已知量、未知量以及它们之间的联系，以寻求解决问题的可能途径．从所要证明的结论来看，要证明的结论AB2+CD2=BC2+AD2=d2(或者AB2+CD2=BC2+AD2=4r2)是一个连等式，于是拟定以下方案：

方案1证明AB2+CD2=BC2+AD2和BC2+AD2=d2；

方案2证明AB2+CD2=BC2+AD2和AB2+CD2=d2；

方案3证明BC2+AD2=d2和AB2+CD2=d2；

方案4证明AB2+CD2=BC2+AD2和BC2+AD2=4r2；

方案5证明AB2+CD2=BC2+AD2和AB2+CD2=4r2；

方案6证明AB2+CD2=4r2和BC2+AD2=4r2．

以上方案均与圆的直径、半径联系密切，因此在证明过程中，要先将圆的直径、半径构造出来.有了直径后通常要构造直径所对的圆周角及圆周角对应的直角三角形，从而就可以用勾股定理.而结论中的AB2+CD2=d2虽然与勾股定理的形式很接近，但是线段AB，CD，d并不在同一个直角三角形中，这时还需通过线段相等把线段AB，CD，d转化在同一个直角三角形中，这样就找到了条件和结论的联系．构造出半径后，想到把半径以及圆内接四边形的边密切联系在一起的勾股定理、垂径定理，然后求证．

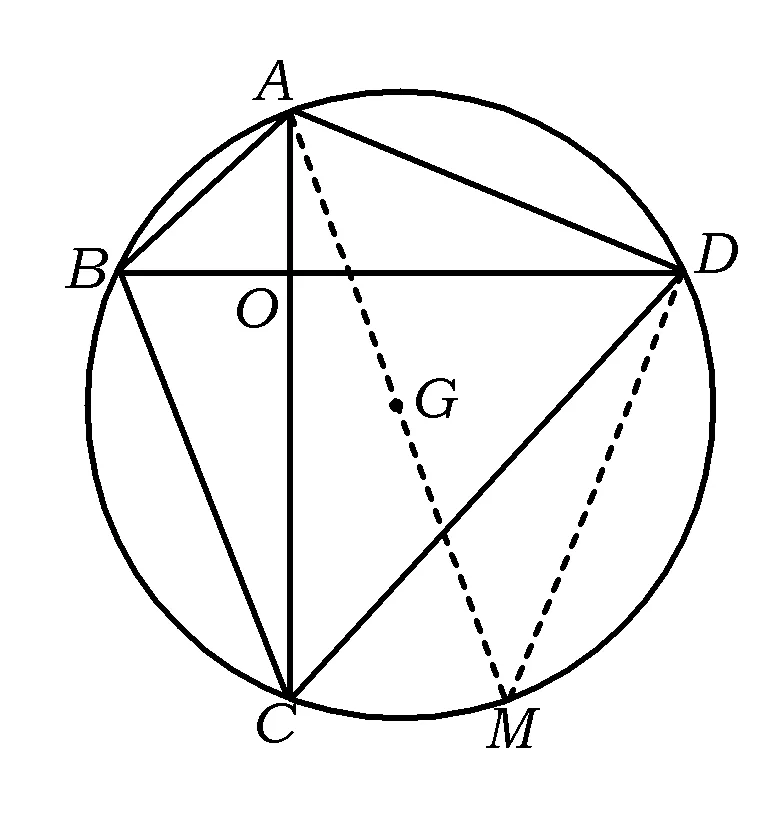
图2

2.3 执行方案

执行方案就是根据拟定的方案进行解题．

对于方案1：首先证明AB2+CD2=BC2+AD2．

如图2，由AC⊥BD，知△DOC,△BOC,△AOB,△DOA是直角三角形.由勾股定理可得

AB2=OB2+OA2，AD2=AO2+OD2，

BC2=BO2+OC2，CD2=OC2+OD2,

从而

AB2+CD2=OB2+OA2+OC2+OD2，

BC2+AD2=BO2+OC2+OA2+OD2,

于是

AB2+CD2=BC2+AD2．

再证BC2+AD2=d2．如图2，作直径AM，联结DM．在⊙G中，

∠ADM=90°， ∠AMD=∠ABD，

又因为∠BAC=90°-∠ABD，∠DAM=90°-∠AMD，所以

∠BAC=∠DAM，

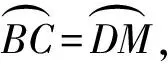
即

BC=DM，

于是

BC2+AD2=DM2+AD2=AM2=d2，

方案1得证．

对于方案2中AB2+CD2=BC2+AD2的证明同方案1．

对于AB2+CD2=d2，可采用以下证法： 如图3，作直径DN，联结CN．在⊙G中，

∠NCD=90°， ∠CAD=∠CND，

又因为∠CDN=90°-∠CND，∠ADB=90°-∠CAD，所以

∠CDN=∠ADB，

即

AB=CN，

于是

AB2+CD2=CN2+CD2=DN2=d2，

方案2得证．

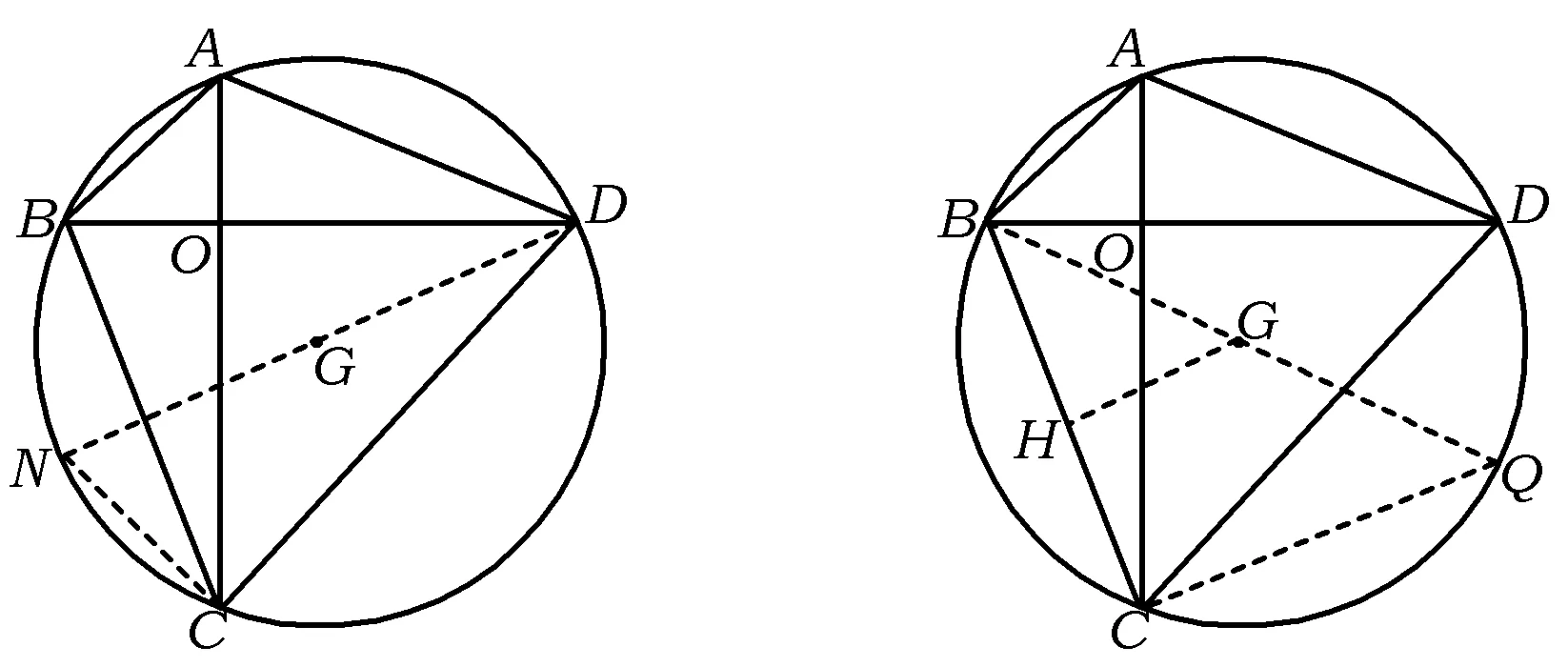
图3 图4

对于方案3：BC2+AD2=d2和AB2+CD2=d2的证明，只要把方案1和方案2证明中的第二部分，整合到一起即可得证．

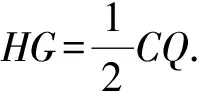
∠BCQ=90°， ∠AOB=90°， ∠BAC=∠BQC,

又因为∠CBQ=90°-∠BQC，∠ABD=90°-∠BAC，所以

∠CBQ=∠ABD，

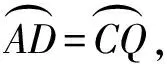
即

AD=CQ，

于是

在Rt△BHG中，

即

BC2+AD2=4r2，

方案4得证．

对于方案5：AB2+CD2=BC2+AD2的证明过程仍同方案1．对于AB2+CD2=4r2的证明如下：

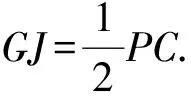
∠DCP=90°， ∠AOD=90°， ∠DAC=∠DPC,

又因为∠CDP=90°-∠DPC，∠ADB=90°-∠DAC，所以

∠CDP=∠ADB，

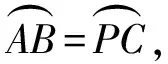
即

AB=PC，

于是

在Rt△DGJ中，

即

AB2+CD2=4r2，

方案5得证．

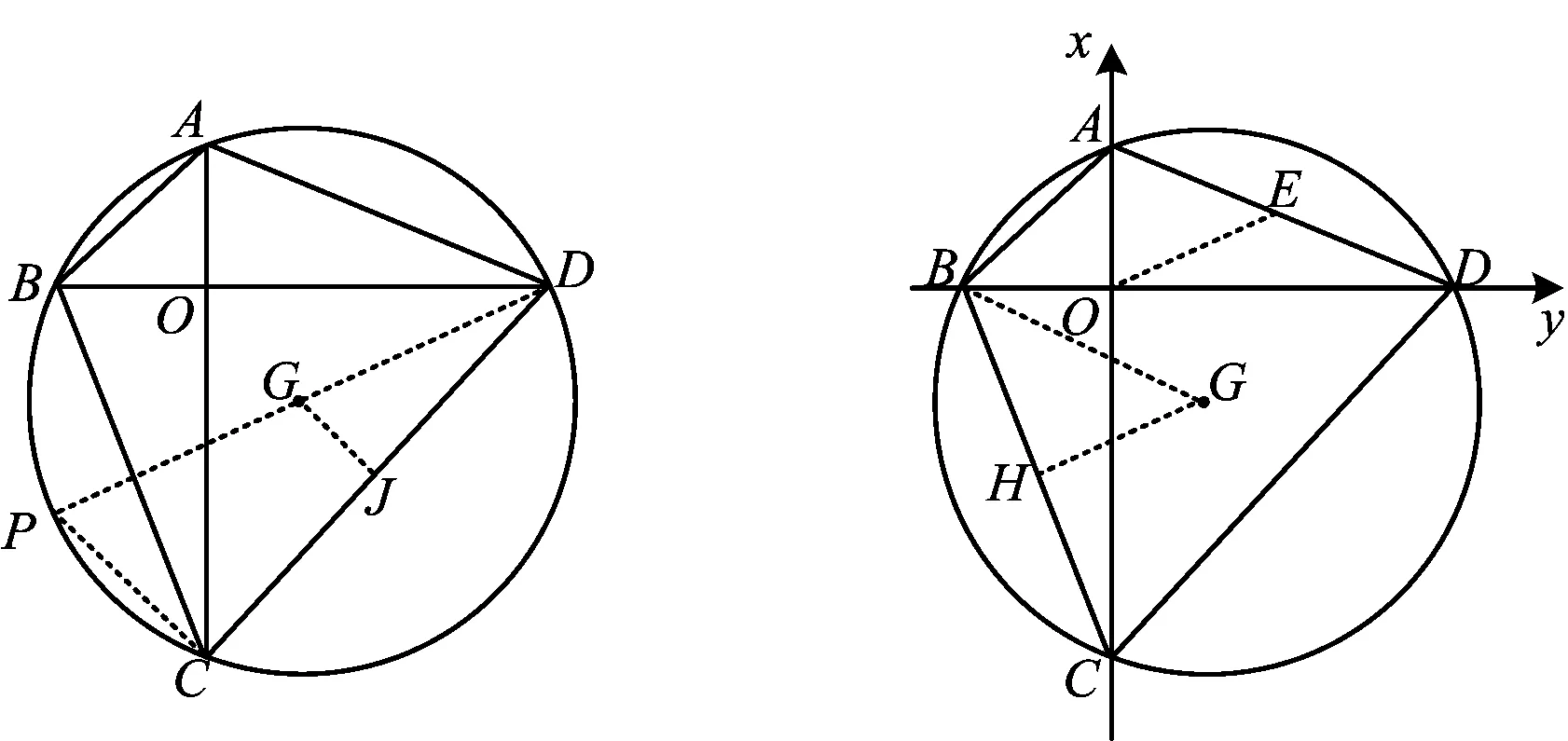
图5 图6

对于方案6：

方法1将方案4中BC2+AD2=4r2的证明和方案5中AB2+CD2=4r2的证明整合到一起即可得证．

方法2以两条对角线的交点为原点、对角线所在直线为坐标轴建立直角坐标系(如图6所示)， 取AD的中点E，联结OE，作GH⊥BC于点H，由垂径定理可知BH=CH．

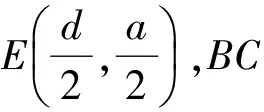
得

OE=HG．

因为△DOA是直角三角形，E为AD的中点，所以

从而

在Rt△BGH中，

从而

即

BC2+AD2=4r2，

同理可得

AB2+CD2=4r2，

于是

AB2+CD2=BC2+AD2=4r2．

当然利用图5坐标系的方法，也可以证明

AB2+CD2=BC2+AD2，

因为A(0，a)，B(-b，0)，C(0，-c)，D(d，0)，所以

AB2=a2+b2，CD2=c2+d2，

AD2=a2+d2,BC2=b2+c2，

从而

AB2+CD2=a2+b2+c2+d2，

BC2+AD2=b2+c2+a2+d2，

即

AB2+CD2=BC2+AD2．

2.4 回顾

回顾此题的解题过程，发现上述解法中构造直径的方法，其实是圆的证明题中常用的方法，这种方法的巧妙之处是能够构造直角三角形，便于与勾股定理联系起来．而方案6的证法，则是巧用坐标系，把几何证明转化为代数证明，体现了数形结合的思想方法，对很多比较难的几何题，构造坐标系是一种行之有效的方法．在证明方案2中结论AB2+CD2=d2时，通过构造Rt△DCN及证明线段相等AB=CN，把不在同一直角三角形中的3条线段AB,CD,d转化在同一直角三角形中，这其实就是转化思想方法．

3 对教学的启示

3.1 解题探究应注重思路探索

解题探究的过程其实就是一种观察、猜想、探索、证明、发现的过程．本题在理解题目时就是通过合情推理猜想出本题的结论，再利用合情推理拟定方案，得出本题的解题思路．在探索思路的过程中，可以让学生思考：是否见过与此题相类似的题目？要解决的问题与以前的类似题有何联系？需要添加辅助线建立联系吗？添加辅助线，可以引申出哪些新的结论？这些新的结论可以成为新题和旧题的桥梁吗？通过这些问题，寻找解题思路，打破思维障碍，从而成功解题．思路的探索其实就是拟定方案的过程，因此教学中应引导学生凭借经验和直觉，通过归纳、类比等推断某些结果，这其实是推理能力中的合情推理，也就是说用合情推理探索思路，发现结论，再用演绎推理证明结论．总之，一道几何证明题应注重探索解题思路，即注重拟定方案的过程，有了解题思路，可谓是成功了一半．

3.2 解题探究应关注思想方法

《义务教育数学课程标准(2011年版)》将“双基”变为“四基”，其中增加的一条就是“基本思想”．数学思想方法是将数学知识转化为数学能力的内在动力，它是数学知识和方法在更高层次上的抽象与概括．传统的数学教学只重视单纯的数学知识的教学，殊不知这样的教学仅仅是学生知识的积累，是会遗忘甚至于消失的，而方法的掌握、思想的形成，才能使学生受益终生，正所谓“授之以鱼，不如授之以渔”．也就是说，学生需要学习的不仅是孤立的一个题目的解法，还有知识的理性内涵与本质意蕴、过程中的关键方法与核心思想[3]．其实波利亚解题步骤的拟定方案的过程，最终是将不熟悉的问题转化为熟悉的问题来探究，这个过程就是一种转化的思想方法.例如：方案1在证明BC2+AD2=d2时，就用了转化的思想方法，将要证明的式子BC2+AD2=d2，转化为与勾股定理相关的式子；方案6中构造坐标系的方法即利用数形结合的思想方法，将几何问题转化为代数问题．

3.3 解题探究应做到解题回顾

解题探究后要重视解题后的反思，教师要引导学生对整个解题过程和涉及到的知识点、辅助线的添加方法进行回顾反思;对解题中发生的错误思路或者是卡壳思路进行分析，对解题的技巧、思想方法进行思考和总结;另外，还可看看解题的过程中是否产生新的结论，新结论可以作为一种经验总结，以备在以后的解题中作为解题的突破口，解题反思可以使学生的解题思路得到开拓，分析问题和解决问题的水平得到进一步的升华．另外，通过引导学生归纳解题方法、技巧、规律和思想方法，能够促进知识向能力的转变，实现自我完善，争取做一题通一法、会一类通一片的效果[4].

在解题教学中，教师应该引导学生借助波利亚解题的4个步骤来思考和解决问题，重在引导学生得到分析问题、解决问题的方案和策略，也就是说根据波利亚解题步骤拟定方案，是解决问题的关键，同时也能培养学生的思维习惯．

[1] 波利亚．怎样解题[M]．涂泓，冯承天，译．上海：上海科技教育出版社，2010．

[2] 杭秉全．从“怎样解题”到“学会解题”[J]．中学数学教学参考：中旬，2015(12)：25．

[3] 章建跃．数学学习与智慧发展[J]．中学数学教学参考：中旬，2015(7)：4-10 ．

[4] 李学军．用本促真 贴地而行——一道高二试题的思考历程[J]．中学教研(数学)，2016(4):27-30．