空间向量的正交分解及坐标表示的教学设计*
2018-01-17
●
(内江师范学院数学与信息科学学院,四川 内江 641112)
2016年9月24—26日,全国首届全日制教育硕士学科教学(数学)专业教学技能大赛(决赛)在山东烟台鲁东大学举行,笔者有幸参加了这次大赛,并荣获二等奖.此次比赛共有4个课题,“空间向量的正交分解及坐标表示”即为其中之一.选用的教材是人教社A版普通高中课程标准试验教科书《数学(选修2-1)》[1].下面是笔者备赛期间,着眼于“平面向量的基本定理及坐标表示”与“空间向量的正交分解及坐标表示”前后教学内容的联系与衔接,对教材中的课题“空间向量的正交分解及坐标表示”作了二次开发和加工,对“空间向量的正交分解及坐标表示”的教学内容进行了补充和调整,对向量符号的含义及表示进行了改动,对该课题的教学过程作了新的设计.
1 教材分析
“空间向量的正交分解及其坐标表示”安排在人教A版《数学(选修2-1)》中,教学内容的顺序是:空间向量正交分解→(特殊到一般)空间向量基本定理→单位正交基底→空间向量的坐标表示,见图1.

图1
本节课的核心基础是“平面向量的基本定理及坐标表示”,此内容安排在人教A版《数学(必修4)》中,其教学内容的顺序为:平面向量基本定理→(受力分析)向量的正交分解→平面向量的坐标表示,见图2.

图2
基于“用教材教”和“创造性地使用教材”等理念,对“平面向量的基本定理及坐标表示”与“空间向量的正交分解及坐标表示”等教材内容进行了认真研读,在准确理解教材编写意图的情况下,对本课题教材内容作了补充和调整如下:根据化归与转化的思想,将空间向量分解为2个平面向量,运用平面向量基本定理→空间向量的正交分解→(通过联想和类比)空间向量坐标表示得到“初定义”→(通过类比)空间向量基本定理→单位正交基底→空间向量坐标表示得到“定义”→范例与练习(练习运用空间向量基本定理解决问题),如图3.

图3
2 教学设计说明
数学教学应以“重数学本质的揭示与思维过程的暴露、重知识的形成过程与知识间的逻辑关系、重数学概念的理解与内化、重数学思想方法的总结与提炼”[2]为理念.据此,首先是整体把握高一和高二教材,弄清楚各个知识单元板块之间的内在联系;其次是准确把握所教内容与学生已有的知识水平和数学学习经验的关系,使教学内容、知识顺序更加符合学生的认知逻辑.
基于理解教材、尊重教材,但也不拘泥于教材的二次开发、加工与改动,在“空间向量的正交分解及坐标表示”的教学设计中,调整教学内容的呈现顺序.为了学生能够在高一学习经验基础上积极主动地建构高二新知识,一些向量的符号仍用高一的符号(详见教学过程设计),这样做的好处在于:学生能够充分利用已有知识经验同化新知识,否则,高一的符号系统对高二新学内容不仅没有正面帮助反而有负迁移,这显然不符合认知逻辑.
3 教学过程设计
3.1 复习旧知
1)平面向量基本定理:平面内任意一个向量a,都可以用两个不共线的向量表示,即有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2,其中e1,e2是同一平面内两个不共线的向量.
2)平面向量的坐标表示:设i,j是与x轴、y轴方向相同的单位向量,对于平面内任意一个向量a,若a=xi+yj,则有序数对(x,y)叫做向量a的坐标,记作a=(x,y).
设计意图将已学过的知识不断提取和再现,对旧知进行归纳整理、巩固提高、融会贯通,这样做的目的是为了恢复或强化头脑里已形成的知识经验,从而对其进行组块的再加工,以期将新知识与学习者认知结构中已有的适当观念建立起实质性的联系.
问题1平面向量的坐标能否推广到空间?
设计意图布鲁纳发现学习理论认为:认识是一个过程而不是一种结果,因此让学生依据所获得的“感性材料”(如平面向量的坐标表示),借助推理和直觉思维提出试探性的假设(如平面向量坐标的推广),无疑是培养学生发现能力的重要环节.
3.2 探究新知
3.2.1 空间向量的正交分解

图4


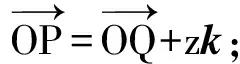
在i,j所确定的平面上,存在有序实数对(x,y),使得

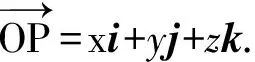
设计意图1)此处向量i,j,k与教材中采用的符号不同,我们采用的i,j,k不仅两两垂直,而且都是单位向量.追本溯源,向量i,j曾以“与x轴、y轴方向相同的两个单位向量i,j作为基底”首次出现在人教A版《数学(必修4)》“平面向量的正交分解及其坐标表示”中[3].为避免引起学生混乱,以及预防学生对新知识的学习产生负迁移,故仍沿用向量i,j,k是两两垂直的单位向量.
2)将空间中任意一个向量分解为两个向量:一个是xOy平面上的向量,一个是与z轴共线的向量(或是与k所确定的平面上的向量);再由平面向量基本定理,将空间中的任意一个向量分解为3个互相垂直的向量,叫做空间向量的正交分解.
3)让学生充分体会蕴涵在问题解决过程中的化归与转化、符号化、数形结合等数学思想,以及欣赏演绎推理、逻辑证明的数学魅力,养成言之有理、论证有据的习惯.
3.2.2 空间向量坐标表示的定义(此定义称为“初定义”)



3)这里所给的定义是基于联想和类比得到的,属于直觉性的定义.
3.2.3 空间向量基本定理
问题3平面向量基本定理能否推广到空间?
定理1如果3个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc.其中,{a,b,c}叫做空间的一个基底,a,b,c叫做基向量.
设计意图开普勒说:我珍视类比胜过任何别的东西,它是我最可信赖的老师,它能揭示自然界的秘密[4].类比作为一般的科学方法,是人们探索问题、寻求和发现真理的重要方法.学生认为新的数学问题情境与先前的问题情境类似或相仿,就可能产生类比[5].通过类比平面向量基本定理,进而推广得到空间向量基本定理.注意:空间任何3个不共面的向量都可作为一个基底.
3.2.4 空间向量坐标表示的“定义”
问题4能否直接用空间向量基本定理推出空间向量的坐标表示?
1)单位正交基底.
“定义” 设i,j,k为有公共起点O的3个两两垂直的单位向量,则i,j,k称为单位正交基底.
设计意图此处将教材中“设e1,e2,e3为有公共起点O的3个两两垂直的单位向量,称为单位正交基底[1]”中的“e1,e2,e3”更改为学生已经学过的i,j,再添上新符号k,就构成“i,j,k”.这样做的原因是:若在40分钟的同一节课中,“e1,e2,e3”中的“e1,e2”就以“两两垂直的单位向量”出现,则违背逻辑学中的同一律,即同一个词语、同一个符号它们的意义(含义)必须保持同一性,即同一词语意义的同一性,相同符号含义的一致性[6].
为遵循同一性,避免学生引起混乱,以学生原有的认知结构、知识经验为基础,将“e1,e2,e3”更改为“i,j,k”.需要说明的是,符号这样更改,高一的符号系统对高二新学内容能够产生正迁移,符合认知逻辑.
2)空间向量的坐标表示.

因为点P的位置由空间向量p唯一确定,所以向量p的坐标恰是点P在空间直角坐标系Oxyz中的坐标(x,y,z),这样便有了从正交基底到直角坐标系的转换.
设计意图联想一些形式相同、思考方法接近、结构特征相似的熟悉问题或常规问题,通过迁移将会顿悟出解决问题的思路和方法[6].联想空间向量基本定理与平面向量的坐标表示等“熟悉问题”,通过从一般到特殊的演绎推理,得到空间向量坐标表示的再定义.需要特别强调的是,虽然与前面引出空间向量坐标定义的方式不同,但其本质是相同的.
思考由空间向量基本定理知p=xi+yj+zk,及空间向量的坐标表示知p=(x,y,z),是否有xi+yj+zk=(x,y,z)?
设计意图解题的灵活性来源于概念的实质性联系,因此从概念的联系中寻找解决问题的思路[7].如上恒等式,在解题过程中经常反复互用,将其单独提取出来,一是为了培养学生从概念间建立联系的意识,二是为了在已知和未知的多元表征中建立直观刺激.
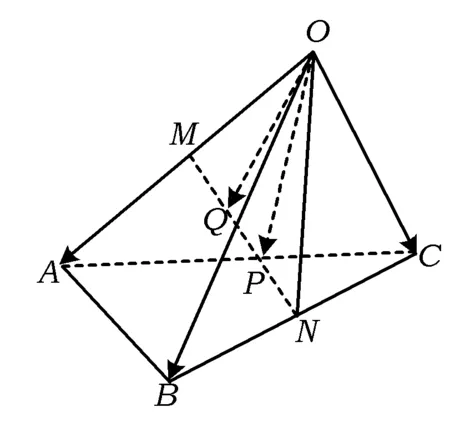
图5
3.3 范例与练习
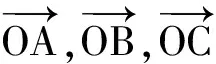
设计意图空间任意一个向量都可以用3个不共面的向量表示出来,这能为解决问题带来方便.范例与练习是理解数学概念的必要步骤.
3.4 总结提炼
1)归纳“空间向量正交分解—坐标表示初定义—空间向量基本定理—单位正交基底及坐标表示再定义”的研究过程,使学生头脑中形成关于本课内容的一个清晰的知识结构,包括相关知识的联系.
2)以空间与平面之间的相互关联为载体,概括用猜想法、联想法、类比法、归纳法、演绎法等研究空间问题的基本方法,以及数形结合、化归转化、符号化等基本思想,让学生体会数学思想和方法蕴含在数学知识发生、发展和应用的过程中.
设计意图围绕本课的内容及其反映的数学思想方法,以知识的发生、发展过程为线索展开,以期及时归纳本课内容,提炼思想方法,总结学习经验,方能维持其时效性和鲜活性.
3.5 课后作业
1)复习本节课所学内容.
2)作业:教材第97页习题A组第1~3题.

4)预习:空间向量运算的坐标表示.
设计意图复习是记忆之母,复习是理解之父,充分理解和记忆所学知识后,能提高应用该知识解决新问题的效率;数学教材中的习题是精挑细选的,且难度循序渐进递增,适量练习是检验所学知识运用和实践情况的有效途径;思考题将思考延伸到课外,培养学生更深层次的学习,体现了分层教学理念,且具有探究意味;预习的主要任务是初步感知新知识,并找出疑难点,为学习新知识埋下伏笔,以达到更好的学习效果.
[1] 刘绍学,王申怀.普通高中课程标准实验教科书·数学(选修2-1)[M].北京:人民教育出版社,2007.
[2] 赵思林.一道公式推导试题引发的争论与思考[J].数学通报,2011,50(9):16-18.
[3] 刘绍学,章建跃.普通高中课程标准实验教科书·数学(必修4)[M].北京:人民教育出版社,2007:93-96.
[4] 钱珮玲,章建跃.普通高中课程标准实验教科书·数学(选修2-2)[M].北京:人民教育出版社,2007.
[5] 赵思林,朱德全.试论数学直觉思维的培养策略[J].数学教育学报,2010,19(1):23-26.
[6] 赵思林,王佩,徐小琴.高中函数定义存在的问题和修订建议[J].教学与管理,2017(1):41-43.
[7] 章建跃.“卡西欧杯”第五届全国高中青年数学教师优秀课观摩与评比活动总结暨大会报告——理解数学理解学生理解教学[J].中国数学教育,2010(12):3-7;15.
