利率调整条件下高频金融时间序列的风险度量

武 东,李 琼

(1.安徽农业大学理学院，安徽合肥230036；2.徽商职业学院 电子信息系，安徽合肥 230022)

一、引言

目前，对月、周、日等低频数据的分析还是国内研究股价变动的主流，主要从股市交易行为、制度因素上和基本面上考虑证券的波动。相较于国外学者对于高频数据较为全面的了解，国内高频模型的建立还并不完善，对于波动剧烈的国内市场也并不能很好把握。鉴于此，研究高频金融时间序列[1]具有十分重要的意义，主要体现在3个方面，主要如下: 第一，在研究过程中可以很好地观察到我国金融市场所具有的一些独特的方面；第二，通过模型的拟合，对于股市的微观结构可以有一个更透彻的了解；第三，可以以此为例指导我国市场投资者投资，避免盲从。

高频金融时间序列除了具有尖峰厚尾特征还具有弱相关性、易变性聚类和杠杆效应等诸多特征。而GARCH类模型有助于刻画这些特征[2,3]。Bollerslev所提出的GARCH模型是将过去的条件方差引入条件方差模型得到的[5]，该模型能较好地计算股票收益率序列的波动率。然而，GARCH模型的条件方差均为过去新息平方的函数, 因此价格的升降变化对条件方差的影响是对称的。但实践中，人们发现当好消息出现时，证券市场波动变化不大，而坏消息出现时，证券市场波动变化增大。Ding等所提出的APARCH模型[6]是一种归纳性很强的非对称模型，它能刻画新息的不对称影响。考虑到我国股市相较于欧美等成熟市场而言变动比较剧烈，影响因素也更加丰富。特别是政府宏观经济政策对股票价格涨跌的作用最为明显。其中包括：利率、税收和货币政策等。本文将广义误差分布融入到APARCH模型，得到基于广义误差分布的APARCH模型，并对沪深指数的高频时间序列建立波动性模型并进行VaR计算。

二、APARCH-GED模型

假设股票的收益率序列{rt},t=1,2,…,T满足以下方程为：

rt=μ+εt,εt=ztσt,

(1)

其中新息zt的分布是零均值单位方差的标准化分布，APARCH模型[7]的数学形式为：

(2)

其中ω>0,αi≥0,βj≥0,i=1,2,…,q,j=1,2,…,p,q≥0,p>0，d(>0)用于对σt进行Box

-Cox变换，γi(-1<γi<1),i=1,2,…,p反映波动变化的杠杆作用。

若条件方差模型中的新息分布为广义误差分布，其概率密度的表达式为：

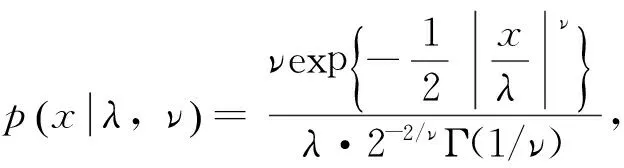
由此可以构建出基于广义误差分布的APARCH模型，记为APGARCH-GED模型。若新息分布分别取为正态分布，则得到基于正态分布的APARCH模型，记为APARCH-N模型。下面利用这两个模型对沪深证券市场的收益率序列进行拟合并考查它们在波动性建模方面的有效性。

三、实证研究

2014年3月1日，中国人民银行放开中国(上海)自由贸易试验区小额外币存款利率上限。对自贸区的先行试水对股市的波动也产生了影响。2014年11月22日，中国人民银行采取非对称方式下调金融机构人民币贷款和存款基准利率。现取沪深300(股票代码399300)的每5分钟收盘价格作为研究对象，银行利率调整对股市收益率及其变化的动荡产生了不容忽视的影响，因此选取2014年3月3日到2014年3月31日的每5分钟收盘价格数据，记为数据一，再选取2014年11月21日至2014年12月22日的每5分钟收盘价格数据，记为数据二，样本容量均为1187。

对上述每5分钟收盘价格利用小波分析对其进行去噪声处理，去噪声后的第t个5分钟价格序列记为Pt, 则第t个5分钟收益率序列为Rt=100(lnPt-lnPt-1)。

表1沪深指数每5分钟收益率序列的描述统计

来源均值标准差最小值最大值偏度峰度数据一3.53e-40.1873-1.09891.18340.27537.3948数据二0.02420.3891-3.33442.8245-1.120124.8014

表1列举了沪深300股指两段每5分钟收益率序列的描述性统计分析的结果，这两段股指每5分钟收益率序列的峰度均大于正态分布的峰度3，呈现尖峰的特征。由此初步判断，该样本数据不服从正态分布。

下面以数据一为例研究每5分钟收益率序列的特征，图1绘制了每5分钟收益率序列的直方图，图中normal, ged分别表示用正态分布和广义误差分布的密度拟合。图2绘制了5分钟收益率序列趋势图，易见序列呈波动聚集特征。从而，本文建议采用基于广义误差分布的APARCH模型对股指收益率序列进行拟合。表2列举了沪深300指数每5分钟收益率序列的APARCH类模型的估计结果。γ1表示模型的杠杆效应系数，所有模型的γ1值都是负数，表明坏消息对股市的影响速度要大于好消息的影响，也反映了负面消息对股市的干扰较强。本文所有APARCH模型的计算采用了R语言软件fGarch宏包完成。

图1 收益率序列的直方图

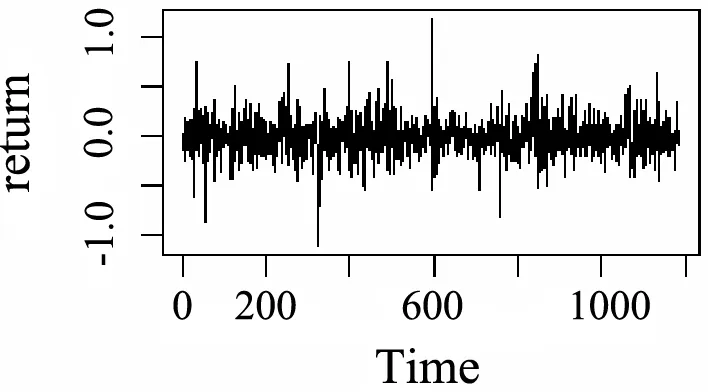
图2 收益率序列趋势图

定义：设某投资组合Z投资一定数额的资产W后，在未来某一持有期T内的损益，则称满足条件P{Z<-VaR}=α的正数VaR为该投资组合在未来持有期T内置信水平为1-α的风险测度[8]。

假设该投资组合在[0,T]时期内的收益率X=Z/W的分布函数为F(x)，且该投资组合的收益率分布的下侧α分位数为xα=sup{x|P{X≤x}≤α}，对于收益率序列{rt}, 可以得到基于APARCH模型的VaR(rt)的计算公式为

VaRα=-(μ+F-1(α)σt)

(3)

表3和表4分别列举了基于APARCH类模型得到每五分钟收益率序列的风险测度结果。下面利用Kupiec似然比检验法[9]验证APARCH类模型的有效性。在Kupiec检验法中，若N为检验样本中损失高于VaR值的次数，n为样本容量。若损失超出VaR值的次数N服从成功概率为1-α的伯努利分布，这里α为风险测度采用的显著性水平，因此失效率f=N/n应等于p。Kupiec检验法的原假设为H0:f=p，相应的似然比统计量为

LR=2{ln[fN(1-f)n-N]-ln[αN(1-α)n-N]}

(4)

Kupiec似然比统计量服从自由度为1的卡方分布。

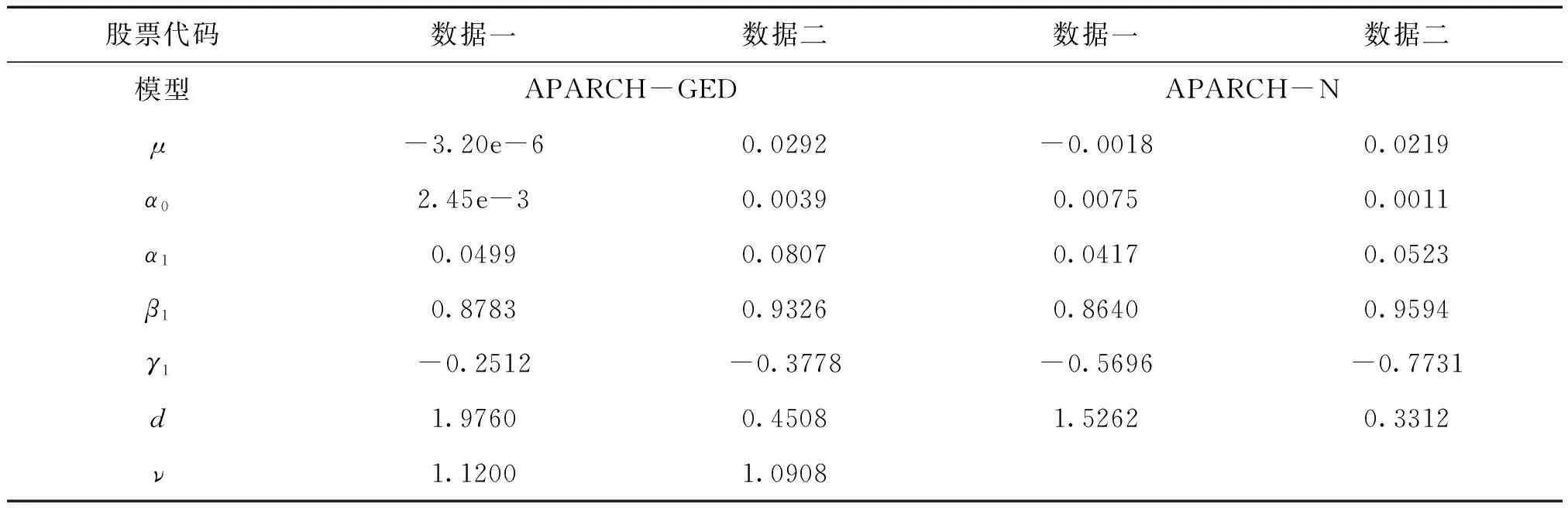
表2 沪深300指数收益率的APARCH类模型的参数估计

表3 基于APARCH类模型的VaR计算

表4 基于APARCH类模型的VaR计算

由表3和表4容易得出下面结论： 第一，由Kupiec检验法的P值可见，在显著性水平0.05下，基于APARCH类模型的VaR都是有效的；当显著性水平为0.005时，所有的APARCH-N模型计算的VaR模型都失效了，而且P值极小，而APARCH-GED模型计算的VaR模型基本有效，说明APARCH-N模型拟合效果欠佳，而APARCH-GED模型能较好地刻画风险；第二，从失效天数和失效比率容易看出，基于APARCH-GED模型计算得到的失效比率更接近显著性水平，而基于APGARCH-N模型计算的失效比率偏离显著性水平较大；第三，从VaR均值比较可见，基于APARCH-GED模型的VaR均值要高于基于APARCH-N模型的VaR均值，说明基于APGARCH-N模型的VaR值会低估了实际的风险值。

综上分析, 可以得出结论：一方面，由于广义误差分布相对于正态分布更具有灵活多变的特征，广义误差分布能较为准确地刻画5分钟收益率序列的尾部特征；另一方面，APGARCH模型是一种概括能力很强的条件异方差模型，形式更加灵活，对5分钟收益率序列的波动率有更强的捕获能力。所以，APARCH-GED模型对证券市场的5分钟收益率序列的拟合度较高, 能较好地刻画其风险特征。

[1] 徐正国，张世英.高频金融时间序列研究：回顾与展望[J].西北农林科技大学(社会科学版)，2005，5(1):62-66.

[2] 武东, 李琼，刘爱国. 稳定分布条件下的动态风险度量模型[J]. 统计与决策，2015,441:23-25.

[3] 张世英, 樊智., 协整理论与波动模型:金融时间序列分析及应用[M].北京:清华大学出版社，2004.

[4] 庄岩.中国农产品价格波动特征的实证研究——基于广义误差分布的ARCH类模型[J].统计与信息论坛，2012，27(6): 59-65.

[5] Bollerslev T.. Generalized autoregressive conditional heteroskedasticity [J]. Journal of Econometrics, 1986, 31: 307-327.

[6] Ding Zhuanxin, Granger,C.W.J., Engle,R.E.. A long memory property of stock market returns and a new model [J]. Jornal of Empirical Finance, 1993, 1: 83-106.

[7] Fernández,C., Steel,M..On Bayesian Modeling of Fat Tails and Skewness[J]. Journal of the American Statistical Association, 1998(93)：359-371.

[8] Jorison P.. Value at Risk: The new benchmark for controlling market risk [M]. New York: McGraw-Hill Companies, 1997.

[9] Kupiec, P.. Techniques for verifying the accuracy of risk measurement models [J]. Journal of Derivatives, 1995, 2:174-184.