传递函数辨识(23):线性回归系统的变间隔递阶递推参数估计

丁锋,刘喜梅

(1.江南大学物联网工程学院,江苏无锡214122;2.青岛科技大学自动化与电子工程学院,山东青岛266061)

系统建模和参数估计是系统分析和设计的基础。系统辨识学术专著[1-7]和连载论文[8-17]中的一些参数估计方法基本都是假设系统的观测数据是均匀采样的,而且在每个采样点数据都是可得到的,即不存在数据丢失情形。然而实际系统由于种种原因,可能造成数据丢失或数据不可信,剔除不可信数据也就产生数据丢失。还有一种情况,数据本身很少能测量到,就是稀少量测数据系统,它也是一类数据丢失较多的损失数据系统。

最近,连载论文研究了线性回归系统的递阶递推辨识方法和递阶递推多新息辨识方法[17]、递阶(多新息)梯度迭代辨识方法和递阶(多新息)最小二乘迭代辨识方法[18]。本工作引入变间隔概念,基于线性回归模型,研究损失数据系统和稀少量测数据系统的变间隔递阶递推辨识方法,包括变间隔递阶随机梯度类辨识方法、变间隔递阶递推梯度类辨识方法、变间隔递阶最小二乘类辨识方法等[7]。提出的变间隔递阶递推辨识方法可以推广用于其他线性和非线性随机系统,以及信号模型的参数辨识[19-21]。

1 线性回归系统的递阶辨识模型

《系统辨识:多新息辨识理论与方法》讨论了变间隔递推辨识方法、变间隔多新息递推辨识方法[6],《系统辨识:辅助模型辨识思想与方法》讨论了变间隔辅助模型递推辨识方法、变间隔辅助模型多新息递推辨识方法[4]。这里讨论线性回归系统的变间隔递阶随机梯度辨识方法、变间隔递阶多新息随机梯度辨识方法、变间隔递阶递推梯度辨识方法、变间隔递阶多新息递推梯度辨识方法、变间隔递阶最小二乘辨识方法、变间隔递阶多新息最小二乘辨识方法。变间隔辨识方法是本研究作者首次提出的,它是通过引入变间隔概念来处理损失数据系统和稀少量测数据系统的辨识问题[22-30]。

考虑下列线性回归系统,

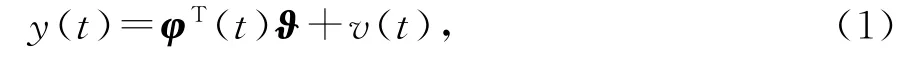
其中y(t)∈ℝ是系统输出变量,v(t)∈ℝ是零均值随机白噪声,ϑ∈ℝn为待辨识的参数向量,φ(t)∈ℝn是由时刻t以前的输出y(t)和时刻t及以前的输入u(t)等变量构成的回归信息向量。假设维数n已知。不特别申明,设t≤0时,各变量的初值为零,这里意味着y(t)＝0,φ(t)＝0,v(t)＝0。

线性回归系统(1)可分解为N个虚拟子系统(fictitious subsystem),即递阶辨识模型(hierarchical identification model,H-ID模型):

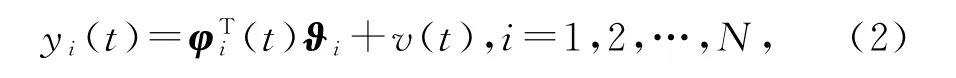
其中子系统参数向量ϑi和信息向量φi(t)与整个系统的参数向量和信息向量的关系如下:

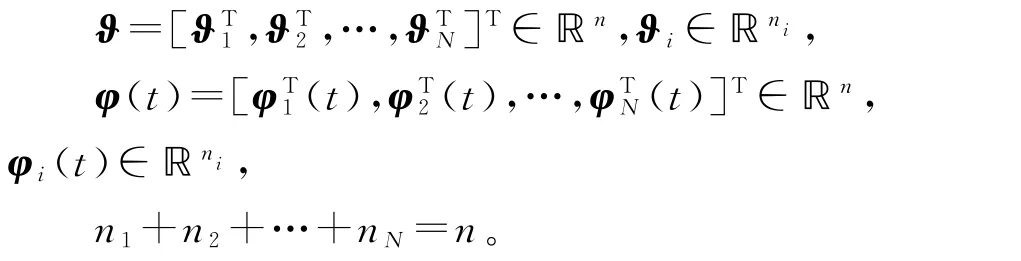
虚拟子系统的输出yi(t)∈ℝ定义为

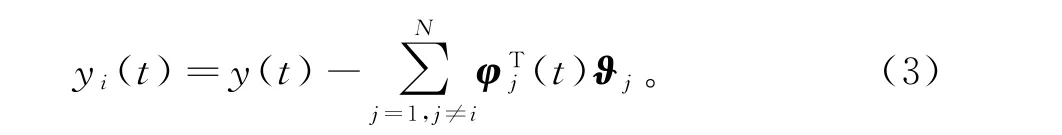
为方便起见,设t为当前时刻,y(t)为当前观测输出,φ(t)为当前观测信息向量,y(t)和φ(t)为当前观测数据。

2 损失数据系统与变间隔辨识方案

在实际中,某些观测数据可能丢失,也就是说由于传感器故障或硬件设备限制,在一些时刻点观测数据得不到,这样的系统称为损失数据系统或稀少量测数据系统。换句话说,对每一个t＝0,1,2,…,观测数据y(t)不总是可得到的系统称为损失数据系统。

为了处理数据丢失和稀少量测数据情形,定义一个整数序列(integer sequence){ts:s＝0,1,2,…},满足

且＝ts－ts－1≥1。假设当t＝ts(s＝0,1,2,…)时,y(t)都可得到,即对所有s＝0,1,2,…,观测y(ts)都可得到,也就是y(t0),y(t1),y(t2),…,都可得到。在这种情况下,数据集{y(ts):s＝0,1,2,…}包含所有可得到的(稀少)观测数据,而不可得到的输出数据{y(ts＋1),y(ts＋2),…,y(ts＋1－1):s＝0,1,2,…}是损失数据[5-6]。

2.1 稀少量测数据情形

与可得到的数据量相比,当丢失的数据占大部分,就称为稀少量测数据系统,如图1所示(图中29个数据点中只有9个数据可得到);当丢失的数据占小部分,就称为损失数据系统,如图2所示(图2中29个数据点中有25个数据可得到,只有4个数据不可得到,还有一个不可信数据)。

图1 稀少量测输出数据情形Fig.1 A scarce output data pattern

对于图1的稀少量测数据情形,可得到的观测输出为

这里t0＝0,t1＝1,t2＝3,t3＝6,t4＝10,t5＝15,t6＝16,t7＝21,t8＝28,…。这是稀少输出量测可得到的一般框架。当然包括对所有s＝1 时所有观测输出可得到的情形[5-6,30-31]。

2.2 损失数据情形

图2是损失输出数据情形(稀少损失数据),＋代表损失输出数据或坏数据(异常数据或不可信数据),y(3),y(8),y(9),y(23),…是损失数据;y(15),…是不可信数据。

图2 损失输出数据情形Fig.2 A missing output data pattern

比较图1和图2可知,稀少量测数据系统意味着大部分数据丢失了,只有少部分数据可得到;相反,损失数据系统意味着少部分数据丢失了,大部分数据可得到。如果系统的输入数据在每一个时刻都可得到,当＝q为大于1的整数时,y(qt)可得到,就得到双率采样数据系统,且输入输出采样数据比为q[32-34]。

2.3 变间隔辨识方案

尽管稀少量测数据系统也是损失数据系统,但在参数辨识时,为了处理丢失数据,需要利用变间隔的观测数据,在多新息辨识算法中需要定义不同的变间隔堆积输出向量和变间隔堆积信息矩阵,所以区分稀少量测数据系统和损失数据系统是必要的。由于观测数据的缺失,提出了变间隔辨识方案,其基本思想是利用可得到的观测数据,研制能处理丢失数据的变间隔递推辨识方法和变间隔迭代辨识方法[32-34]。

3 变间隔递阶随机梯度方法

3.1 变间隔随机梯度辨识算法

对于线性回归辨识模型(1),定义梯度准则函数

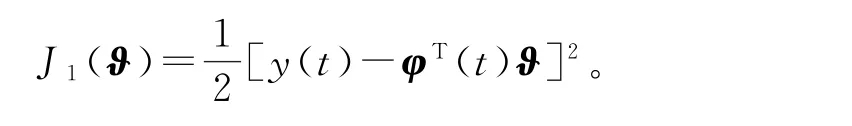
极小化准则函数J1(ϑ),得到辨识系统(1)参数向量ϑ的随机梯度算法(SG 算法):

在数据缺失情形或稀少量测数据情形下,假设可得到的观测数据为y(ts)和φ(ts),s＝0,1,2,…,不可得到的数据为y(ts＋i)和φ(ts＋i),i＝1,2,…,－1,此时SG 算法(4)～(6)不可实现。如果用ts代替式(4)～(6)中的t得到

从s＝1,2,3,…的递推计算过程看,这个算法也不可实现,因为当＞1时,算法中存在未知量(ts－1)。一个可行的办法是用ts代替式(1)中的t,得到一个新的辨识模型

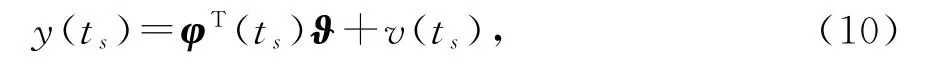
其中y(ts)∈ℝ是可得到的输出数据,φ(ts)是可得到的回归信息向量,v(ts)依旧是零均值随机白噪声。

对线性回归辨识模型(10),定义梯度准则函数

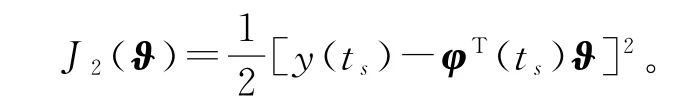
使用负梯度搜索,极小化准则函数J2(ϑ),可以得到辨识系统(1)参数向量ϑ的变间隔随机梯度算法(interval-varying stochastic gradient algorithm,V-SG 算法)[29]:

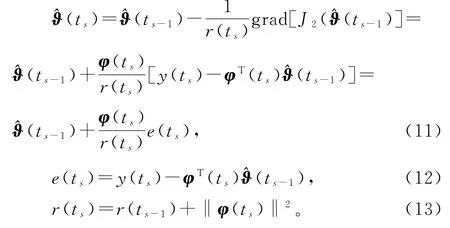
在初始条件(t0)＝1n/p0和r(t0)＝1下,利用可得到的观测信息y(ts)和φ(ts),V-SG 算法(11)～(13)可以递推计算参数估计向量(ts),在数据不可得到时,参数估计保持不变,即

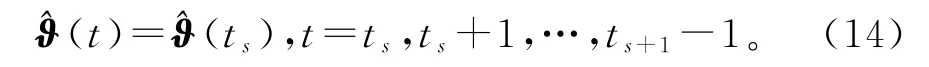
3.2 变间隔递阶随机梯度算法

用ts代替式(2)和(3)中的t,得到变间隔递阶辨识模型:

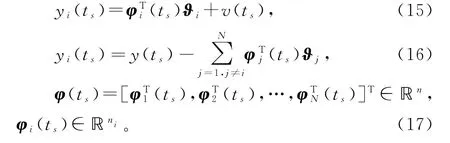
对于递阶辨识模型(15),定义关于子参数向量ϑi的梯度准则函数

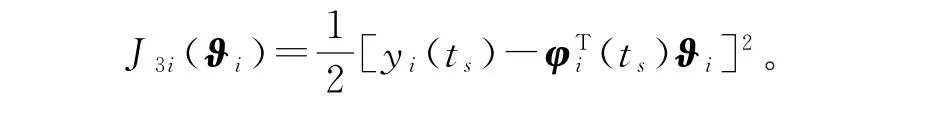
使用负梯度搜索,极小化准则函数J3i(ϑi),可以获得估计参数向量ϑi的梯度递推关系:

注意到观测y(ts)和φ(ts)及其分量φi(ts)是已知的,而虚拟子系统的输出yi(ts)是未知的,故将式(16)中yi(ts)代入式(18)得到

式(20)右边包含了其它子系统的未知子参数向量ϑj(j≠i),所以算法(19)～(20)无法实现。为了实现参数估计(ts)的递推计算,根据递阶辨识原理进行关联项的协调,将式(20)中未知的ϑj用它在前一时刻ts－1的估计(ts－1)代替,可得

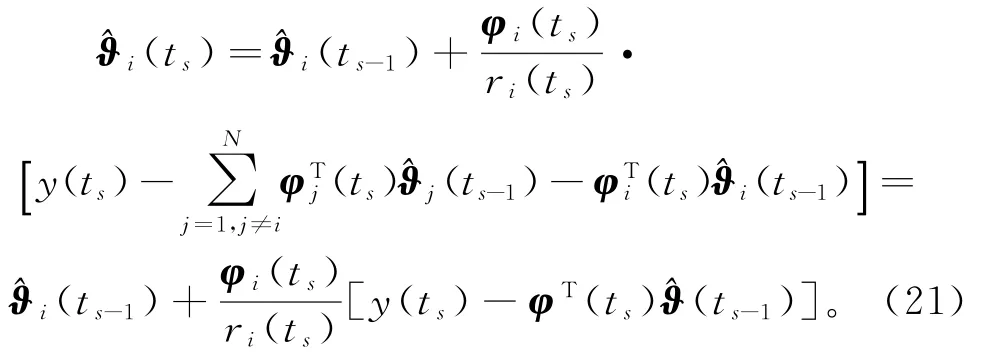
式(21)和式(19)构成了估计系统(1)参数向量ϑ的变间隔递阶随机梯度算法(interval-varying HSG algorithm,V-HSG 算法):

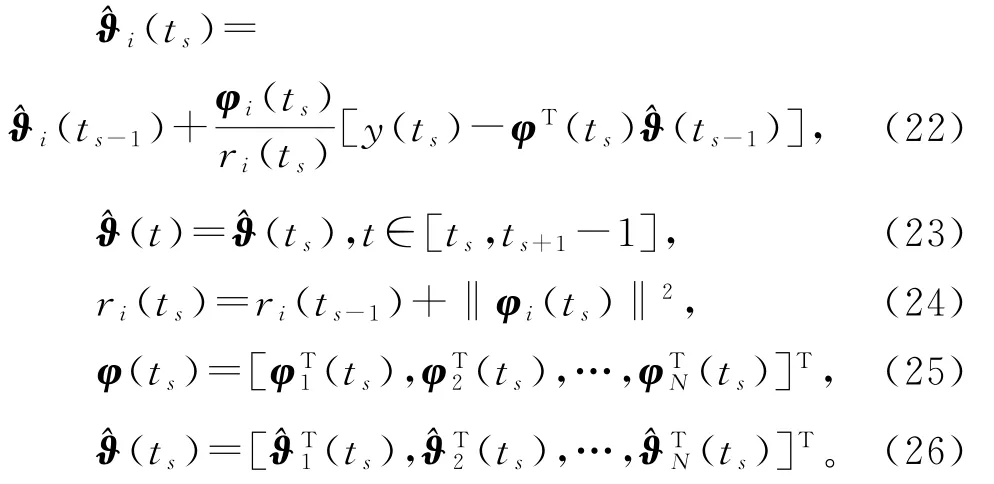
如果式(22)中ri(ts)用式(13)中的r(ts)代替,那么变间隔递阶随机梯度算法(22)～(26)完全等同于变间隔随机梯度算法(11)～(13)。

V-HSG 算法(22)～(26)随s增加计算参数估计的步骤如下。

1)初始化,令t＝1,s＝0,t0＝0。设定N值和ni,置初值。

2)采集观测数据y(t)和φ(t)。

3)如果观测数据y(t)和φ(t)可得到,就跳到下一步;否则置(t)＝(ts),t增加1,即t＝t＋1,转到步骤2)。

4)置s＝s＋1,ts＝t,＝ts－ts－1。从式(25)的φ(ts)中读出子信息向量φi(ts),i＝1,2,…,N。

5)用式(24)计算ri(ts),i＝1,2,…,N。

6)用式(22)刷新参数估计向量(ts),i＝1,2,…,N,根据式(26)构成参数估计向量(ts),根据式(23)令(t)＝(ts)。

7)t增加1,转到步骤2)。

基于V-HSG 算法(22)～(26),在式(22)中引入收敛指数(convergence index)ε,即

就得到变间隔修正递阶随机梯度算法(interval-varying modified HSG algorithm,V-M-HSG 算法)。

基于V-HSG 算法(22)～(26),在式(24)中引入遗忘因子(forgetting factor)λ,即

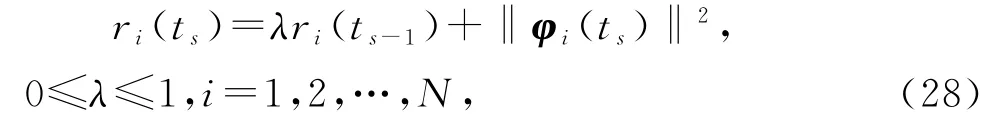
就得到变间隔遗忘因子递阶随机梯度算法(interval-varying forgetting factor HSG algorithm,V-FFHSG 算法)。

基于V-HSG 算法(22)～(26),在式(22)中引入收敛指数(convergence index)ε,在式(24)中引入遗忘因子(forgetting factor)λ,即

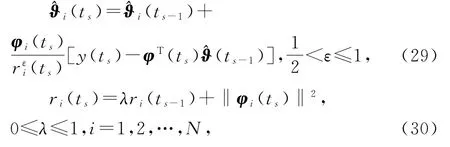
就得到变间隔遗忘因子修正递阶随机梯度算法(interval-varying FF-M-HSG algorithm,V-FF-M-HSG算法)。

4 变间隔递阶多新息随机梯度方法

多新息辨识可以提高梯度算法对数据的利用效率,能提高参数估计精度和收敛速度。这里针对损失数据系统和稀少量测数据系统,讨论变间隔多新息随机梯度辨识方法和变间隔递阶多新息随机梯度辨识方法。

4.1 变间隔多新息随机梯度辨识算法

下面讨论变间隔多新息随机梯度辨识方法,考虑损失数据系统和稀少量测数据系统。4.1.1 损失数据系统

设正整数p为新息长度。对于损失数据系统,假设可得到的观测数据为y(ts),φ(ts),y(ts－1),φ(ts－1),y(ts－2),φ(ts－2),…,y(ts－p＋1),φ(ts－p＋1)。

根据辨识模型(10),利用可得到的观测数据定义堆积输出向量Y(p,ts)和堆积信息矩阵Φ(p,ts)如下:

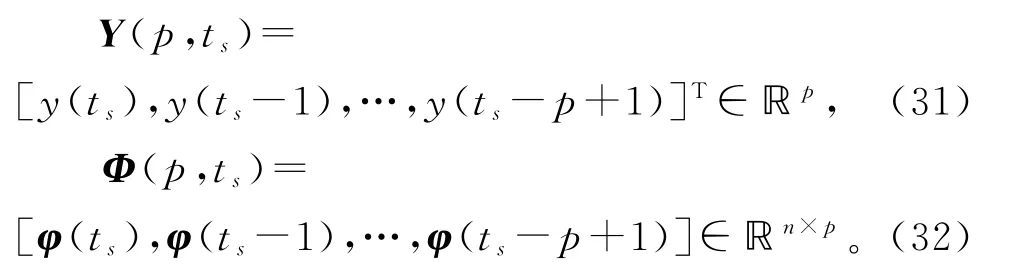
这里基于V-SG 算法(11)～(14),引入新息长度(innovation length),将式(11)中标量新息(innovation)e(ts)＝y(ts)－φT(ts)(ts－1)∈ℝ 扩展为新息向量(innovation vector)

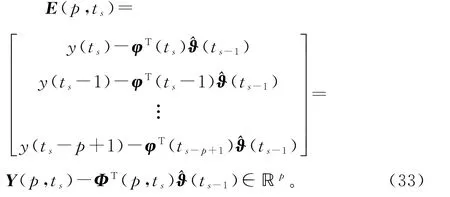
因为E(1,ts)＝e(ts),Φ(1,ts)＝φ(ts),Y(1,ts)＝y(ts),所以式(22)可以等价写为

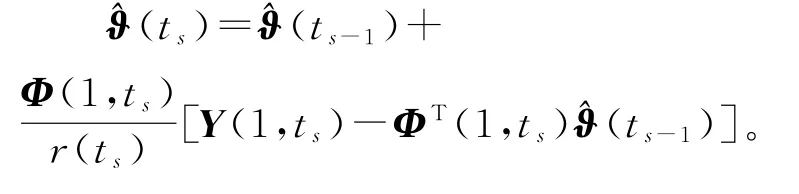
把(1,ts)换为(p,ts),得到

联立式(31)～(34)和式(13),就得到辨识线性回归损失数据系统(1)参数向量ϑ的变间隔多新息随机梯度算法(interval-varying MISG algorithm,V-MISG 算法):

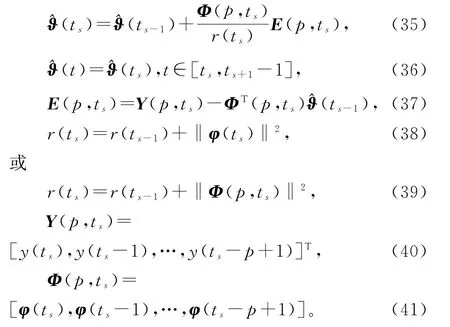
当新息长度p＝1时,V-MISG 算法退化为VSG 算法(11)～(13)。当新息长度p＝1,间隔≡1时,V-MISG 算法退化为SG 算法(4)～(6)。

基于V-MISG 算法(35)～(41),在式(35)中引入收敛指数ε,即

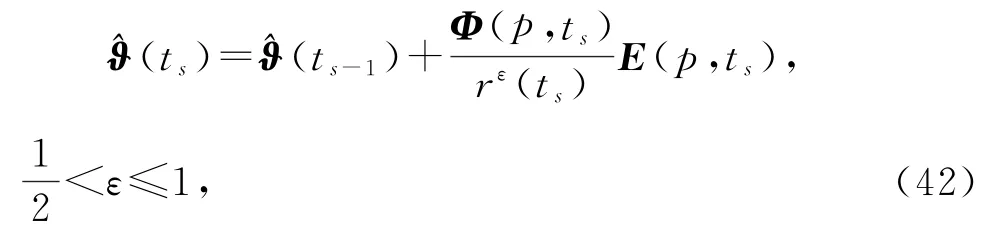
就得到变间隔修正多新息随机梯度算法(intervalvarying M-MISG algorithm,V-M-MISG 算法)。

基于V-MISG 算法(35)～(41),在式(38)～(39)中引入遗忘因子λ,即

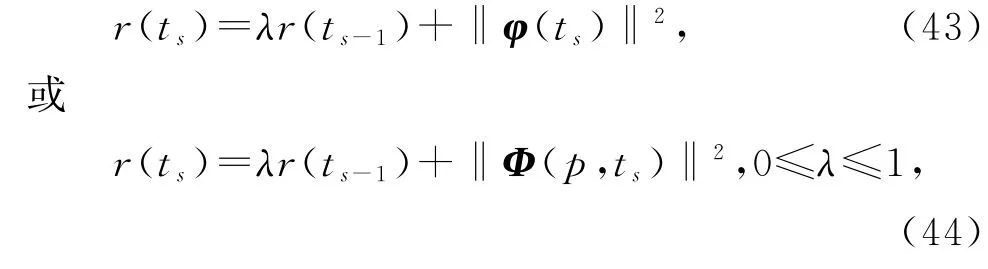
就得到变间隔遗忘因子多新息随机梯度算法(interval-varying FF-MISG algorithm,V-FF-MISG 算法)。

基于V-MISG 算法(35)～(41),在式(35)中引入收敛指数ε,在式(38)～(39)中引入遗忘因子λ,即

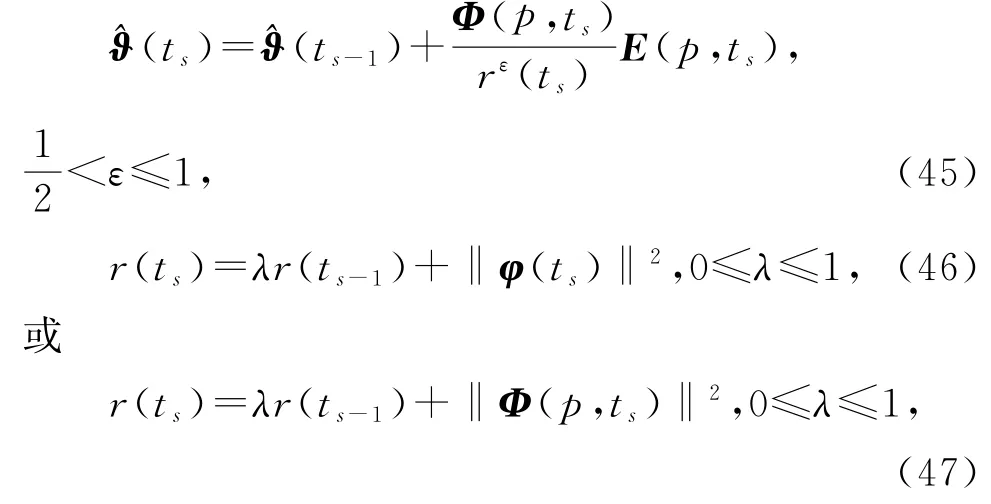
就得到变间隔遗忘因子修正多新息随机梯度算法(interval-varying FF-M-MISG algorithm,V-FF-MMISG 算法)。

4.1.2 稀少量测数据系统

对于稀少量测数据系统,假设可得到的观测数据为y(ts)和φ(ts),s＝1,2,3,…。

设正整数p为新息长度。根据辨识模型(10),利用可得到的观测数据定义堆积输出向量Y(p,ts)和堆积信息矩阵Φ(p,ts)如下:

这里基于V-SG算法(11)～(14),引入新息长度(innovation length),将式(11)中标量新息e(ts)＝y(ts)－φT(ts)(ts－1)∈ℝ扩展为新息向量E(p,ts),仿照线性回归损失数据系统的变间隔多新息随机梯度算法(35)～(41)的推导,可以得到辨识线性回归稀少量测数据系统(1)参数向量ϑ的变间隔多新息随机梯度算法(V-MISG 算法):

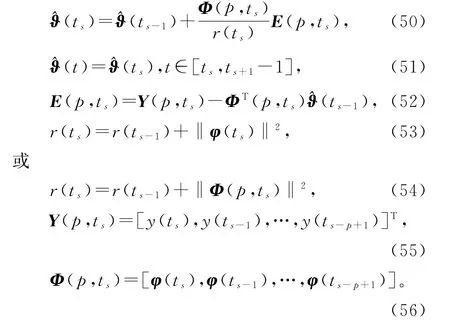
基于稀少量测数据系统的V-MISG 算法(50)～(56),引入收敛指数,加权因子ws≥0,遗忘因子0≤λ≤1,可以得到辨识线性回归稀少量测数据系统(1)参数向量ϑ的变间隔加权遗忘因子修正多新息随机梯度算法(V-W-FF-M-MISG 算法):

当收敛指数ε,加权因子ws,遗忘因子λ取一些特殊值时,V-W-FF-M-MISG 算法(57)～(63)可以派生出变间隔多新息随机梯度(V-MISG)算法、变间隔修正多新息随机梯度(V-M-MISG)算法、变间隔加权多新息随机梯度(V-W-MISG)算法、变间隔遗忘因子多新息随机梯度(V-FF-MISG)算法、变间隔加权修正多新息随机梯度(V-W-M-MISG)算法、变间隔遗忘因子修正多新息随机梯度(V-FF-MMISG)算法等。

4.2 变间隔递阶多新息随机梯度算法

以下讨论变间隔递阶多新息随机梯度辨识方法,考虑损失数据系统和稀少量测数据系统两种情况。

4.2.1 损失数据系统

设正整数p为新息长度。对于损失数据系统,假设可得到的观测数据为y(ts),φ(ts),y(ts－1),φ(ts－1),y(ts－2),φ(ts－2),…,y(ts－p＋1),φ(ts－p＋1)。

根据辨识模型(10)和(15),利用可得到的观测数据定义堆积输出向量Y(p,ts),堆积信息矩阵Φ(p,ts)和堆积子信息矩阵Φi(p,ts)如下:

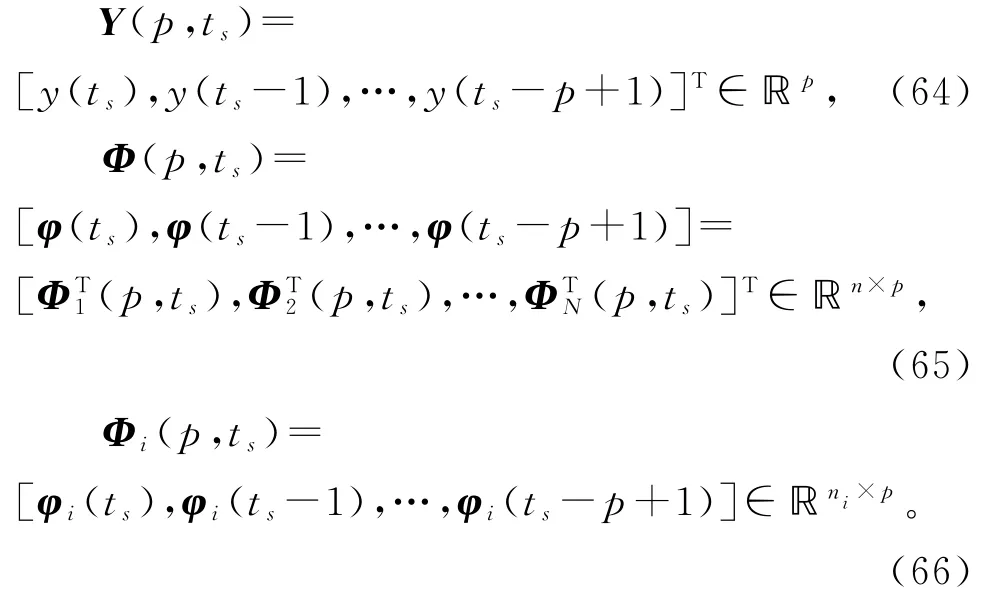
这里基于V-HSG 算法(22)～(26),引入新息长度(innovation length),将式(22)中标量新息(innovation)e(ts)＝y(ts)－φT(ts)(ts－1)∈ℝ扩展为新息向量(innovation vector)

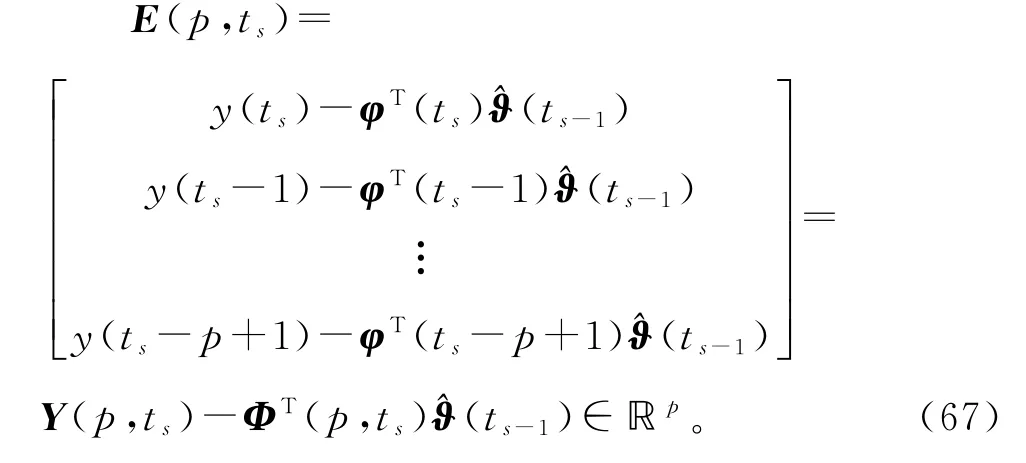
因为E(1,ts)＝e(ts),Φ(1,ts)＝φ(ts),Φi(1,ts)＝φi(ts),Y(1,ts)＝y(ts),所以式(22)可以等价写为

把上式中的(1,ts)换为(p,ts),得到

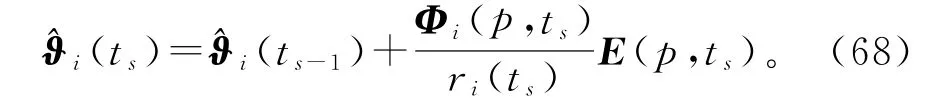
联立式(23)～(26)和(64)～(68),就得到辨识线性回归损失数据系统(1)参数向量ϑ的变间隔递阶多新息随机梯度算法(interval-varying HMISG algorithm,V-HMISG 算法):

当新息长度p＝1 时,V-HMISG 算法退化为V-HSG 算法(22)～(26)。当新息长度p＝1,间隔≡1时,V-HMISG 算法退化为HSG 算法。

基于V-HMISG 算法(69)～(78),在式(69)中引入收敛指数ε,即

就得到变间隔修正递阶多新息随机梯度算法(interval-varying M-HMISG algorithm,V-M-HMISG 算法)。

基于V-HMISG 算法(69)～(78),在式(72)和(73)中引入遗忘因子λ,即

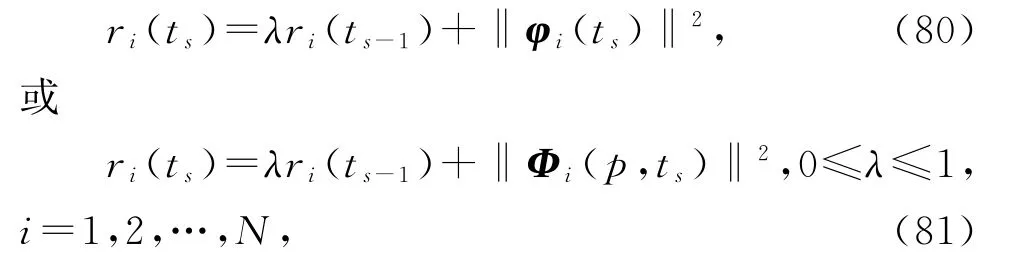
就得到变间隔遗忘因子递阶多新息随机梯度算法(interval-varying FF-HMISG algorithm,V-FFHMISG 算法)。

基于V-HMISG 算法(69)～(78),在式(69)中引入收敛指数ε,在式(72)和(73)中引入遗忘因子λ,即

就得到变间隔遗忘因子修正递阶多新息随机梯度算法(interval-varying FF-M-HMISG algorithm,VFF-M-HMISG 算法)。

4.2.2 稀少量测数据系统

对于稀少量测数据系统,假设可得到的观测数据为y(ts)和φ(ts),s＝1,2,3,…。

设正整数p为新息长度。根据辨识模型(10)和(15),利用可得到的观测数据定义堆积输出向量Y(p,ts),堆积信息矩阵Φ(p,ts)和堆积子信息矩阵Φi(p,ts)如下:

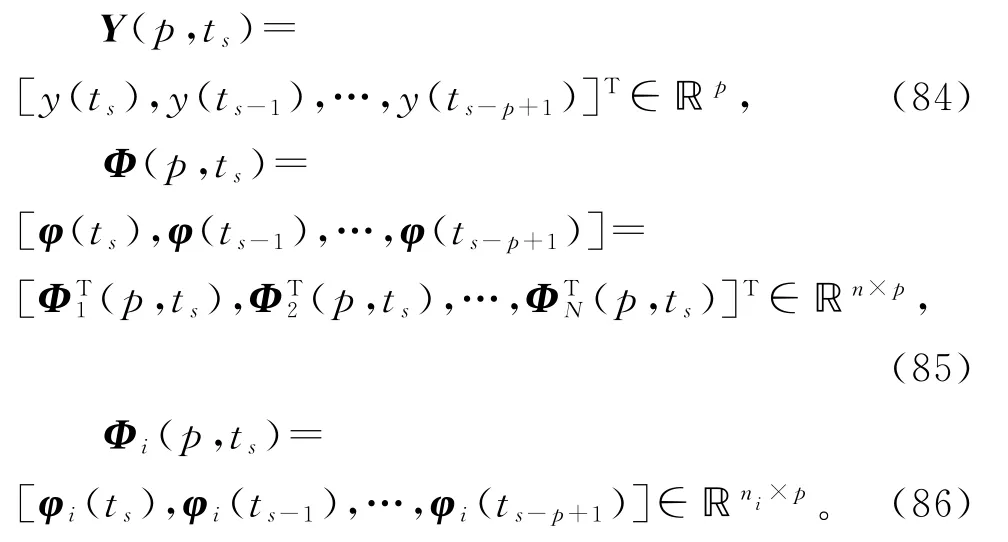
基于HSG 算法(22)～(26),引入新息长度(innovation length),仿照线性回归损失数据系统的递阶多新息随机梯度算法(69)～(78)的推导,可以得到辨识线性回归稀少量测数据系统(1)参数向量ϑ的变间隔递阶多新息随机梯度算法(V-HMISG 算法):

V-HMISG 算法(87)～(96)随s增加计算参数估计的步骤如下。

1)初始化,令t＝1,s＝0,t0＝0。设定新息长度p,设定N和ni,置初值。假设y(t0－j)＝0,φ(t0－j)＝0,j＝0,1,…,p－1。

2)采集观测数据y(t)和φ(t)。

3)如果观测数据y(t)和φ(t)可得到,就跳到下一步;否则置(t)＝(ts),t增加1,即t＝t＋1,转到步骤2)。

4)置s＝s＋1,ts＝t,＝ts－ts－1,从式(95)的φ(ts)中读出子信息向量φi(ts),用式(92)构造堆积输出向量Y(p,ts),用式(93)构造堆积信息矩阵Φ(p,ts)。用式(94)构造堆积信息矩阵Φi(p,ts),i＝1,2,…,N。

5)用式(90)计算ri(ts),i＝1,2,…,N。用式(89)计算新息向量E(p,ts)。

6)用式(87)刷新参数估计向量(ts),i＝1,2,…,N,根据式(96)构成参数估计向量(ts),根据式(88)令(t)＝(ts)。

7)t增加1,转到步骤2)。

基于稀少量测数据系统的V-HMISG算法(87)～(96),引入收敛指数,加权因子ws≥0,遗忘因子0≤λ≤1,可以得到辨识线性回归稀少量测数据系统(1)参数向量ϑ的变间隔加权遗忘因子修正递阶多新息随机梯度算法(V-W-FF-M-HMISG 算法):

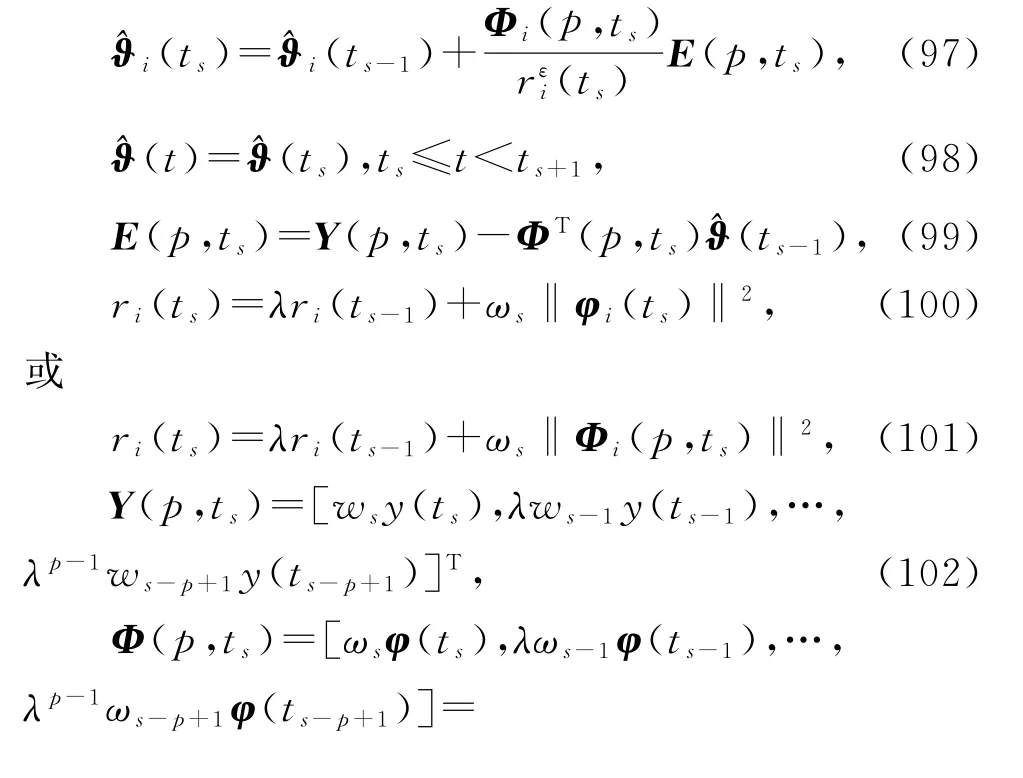
有多种方式引入遗忘因子和加权因子。式(102)～(104)可以修改为

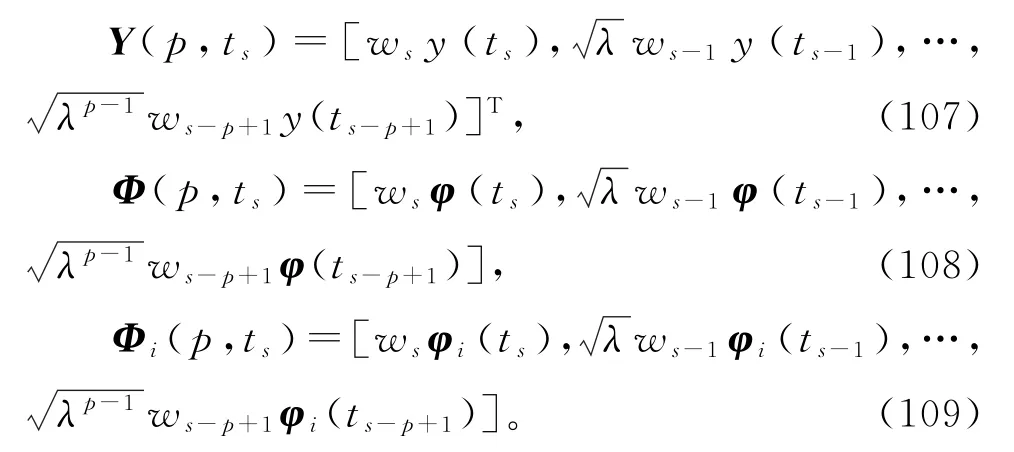
当收敛指数ε,加权因子ws,遗忘因子λ取一些特殊值时,V-W-FF-M-HMISG 算法(97)～(106)可以派生出变间隔递阶多新息随机梯度(VHMISG)算法、变间隔修正递阶多新息随机梯度(VM-HMISG)算法、变间隔加权递阶多新息随机梯度(V-W-HMISG)算法、变间隔遗忘因子递阶多新息随机梯度(V-FF-HMISG)算法、变间隔加权修正递阶多新息随机梯度(V-W-M-HMISG)算法、变间隔遗忘因子修正递阶多新息随机梯度(V-FF-MHMISG)算法等。

5 变间隔递阶递推梯度辨识方法

5.1 变间隔递推梯度辨识算法

用ts代替式(1)中的t,得到变间隔辨识模型

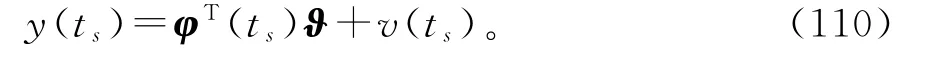
对于变间隔辨识模型(110),定义随时间s递增的准则函数为

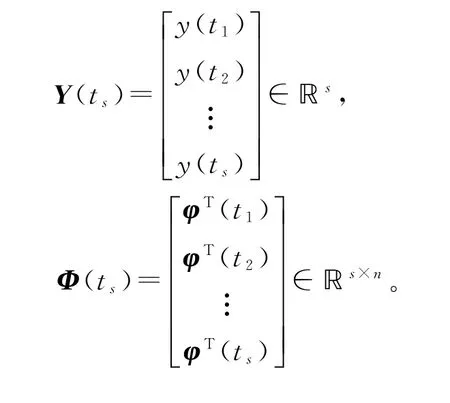
定义堆积输出信息向量Y(ts)和堆积信息矩阵Φ(ts)如下:

那么准则函数J4(ϑ)可以表示为

定义递推关系:

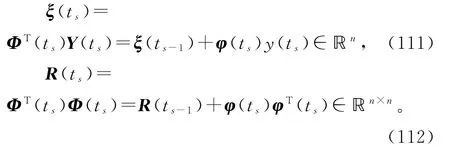
令(ts)∈ℝn表示参数向量ϑ在时刻t＝ts的递推估计。使用梯度搜索,极小化准则函数J4(ϑ),可以得到辨识系统(1)参数向量ϑ的变间隔递推梯度算法(interval-varying recursive gradient algorithm,V-RG 算法)[5]:

读者可以写出引入收敛指数、加权因子、遗忘因子后的变间隔修正递推梯度(V-M-RG)算法、变间隔加权递推梯度(V-W-RG)算法、变间隔遗忘因子递推梯度(V-FF-RG)算法、变间隔加权修正递推梯度(V-W-M-RG)算法、变间隔遗忘因子修正递推梯度(V-FF-M-RG)算法、变间隔加权遗忘因子修正递推梯度(V-W-FF-M-RG)算法。

5.2 变间隔递阶递推梯度算法

这里介绍变间隔递阶递推梯度辨识方法,简称变间隔递阶梯度辨识方法。用ts代替式(2)和(3)中的t,得到变间隔递阶辨识模型:

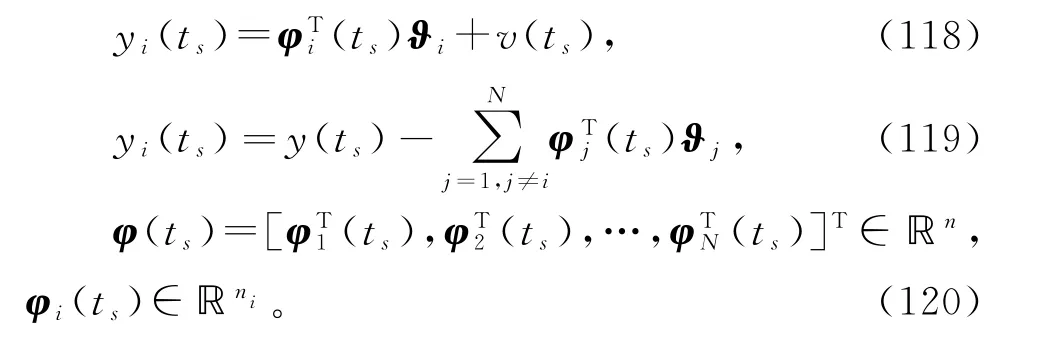
令(ts)∈ℝni是子参数向量ϑi在时刻t＝ts的估计(ts)∈ℝn是参数向量ϑ在时刻t＝ts的估计,即ℝn。

基于辨识模型(110)和(118),定义N个随时间ts递增的准则函数:

定义堆积输出信息向量Y(ts)和Yi(ts),以及堆积信息矩阵Φ(ts)和子信息矩阵Φi(ts)如下:

那么准则函数J5i(ϑi)可以表示为

定义递推关系:

使用负梯度搜索,极小化准则函数J5i(ϑi),可以得到基于梯度的递推关系[5]:

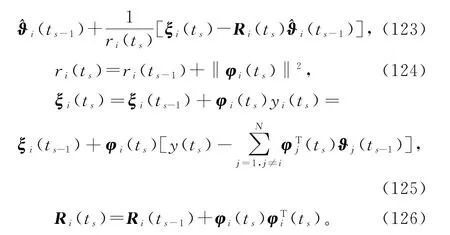
注意到式(125)右边包含了未知关联参数ϑj(j≠i),所以这个算法无法实现。为此应用递阶辨识原理,用它们前一时刻的估计(ts－1)代替,得到式(130),联立式(123)～(124)和(126),便得到辨识系统(1)参数向量ϑ的变间隔递阶递推梯度算法(interval-varying hierarchical recursive gradient algorithm,V-HRG 算法),简称变间隔递阶梯度算法(interval-varying hierarchical gradient algorithm,V-HG算法):

读者可以写出引入收敛指数、加权因子、遗忘因子后的变间隔修正递阶梯度(V-M-HG)算法、变间隔加权递阶梯度法(V-W-HG)算法、变间隔遗忘因子递阶梯度(V-FF-HG)算法、变间隔加权修正递阶梯度(V-W-M-HG)算法、变间隔遗忘因子修正递阶梯度(V-FF-M-HG)算法、变间隔加权遗忘因子修正递阶梯度(V-W-FF-M-HG)算法。

6 变间隔递阶多新息递推梯度方法

这里针对损失数据系统和稀少量测数据系统,讨论变间隔多新息递推梯度辨识方法、变间隔递阶多新息递推梯度辨识方法。

6.1 变间隔多新息递推梯度辨识算法

6.1.1 损失数据系统

多新息辨识方法是考虑最近的p组数据推导出的辨识算法,其中正整数p为新息长度。对于损失数据系统,假设可得到的最新p组观测数据为

设t＝ts为当前时刻。根据变间隔辨识模型(110),利用最新可得到的p组观测数据定义堆积输出向量Y(p,ts)和堆积信息矩阵Φ(p,ts)如下:

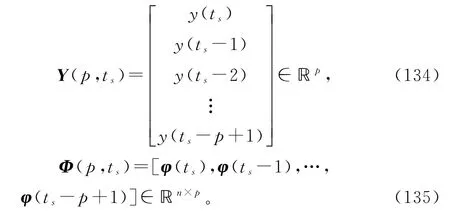
多新息梯度算法采用的随时间s递增的准则函数为

定义堆积输出信息向量Zt和堆积信息矩阵Ωt如下:

则准则函数J6(ϑ)可以写为

求准则函数J6(ϑ)对参数向量ϑ的一阶偏导数,可以得到准则函数J6(ϑ)的梯度向量

令(ts)∈ℝn表示参数向量ϑ在时刻t＝ts的递推估计。在ϑ＝(ts－1)点的梯度为

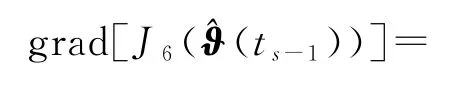
仿照递推梯度辨识算法的推导,可以得到辨识线性回归损失数据系统(1)参数向量ϑ的变间隔多新息递推梯度算法(interval-varying MIRG algorithm,V-MIRG 算法),简称变间隔多新息梯度算法(interval-varying multi-innovation gradient algorithm,V-MIG 算法):

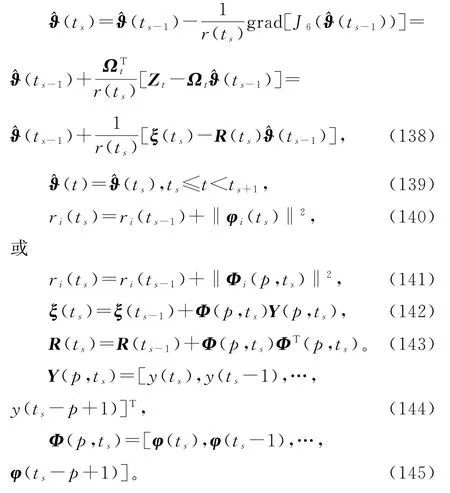
在变间隔多新息梯度辨识算法(138)～(145)中引入收敛指数、遗忘因子,便得到变间隔修正多新息梯度(V-M-MIG)算法、变间隔遗忘因子多新息梯度(V-FF-MIG)算法、变间隔遗忘因子修正多新息梯度(V-FF-M-MIG)算法等。6.1.2 稀少量测数据系统

对于稀少量测数据系统,假设可得到的观测数据为y(ts)和φ(ts),s＝1,2,3,…。设正整数p为新息长度。根据变间隔辨识模型(110),利用可得到的观测数据定义堆积输出向量Y(p,ts)和堆积信息矩阵Φ(p,ts)如下:

仿照递推梯度辨识算法的推导,可以得到辨识线性回归稀少量测数据系统(1)参数向量ϑ的变间隔多新息递推梯度算法(V-MIRG 算法),或称变间隔递推多新息梯度算法(V-RMIG 算法),简称变间隔多新息梯度算法(V-MIG 算法):

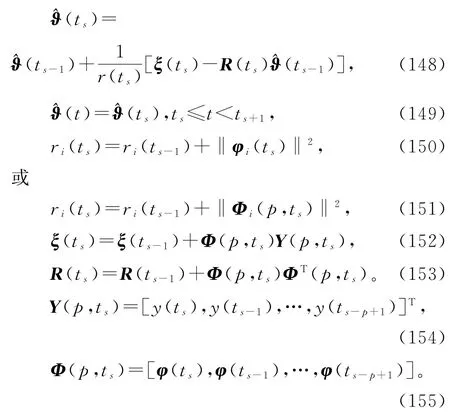
在变间隔多新息梯度辨识算法(148)～(155)中引入收敛指数、加权因子、遗忘因子,便得到变间隔修正多新息梯度(V-M-MIG)算法、变间隔加权多新息梯度(V-W-MIG)算法、变间隔遗忘因子多新息梯度(V-FF-MIG)算法、变间隔加权修正多新息梯度(V-W-M-MIG)算法、变间隔遗忘因子修正多新息梯度(V-FF-M-MIG)算法、变间隔加权遗忘因子多新息梯度(V-W-FF-MIG)算法、变间隔加权遗忘因子修正多新息梯度(V-W-FF-M-MIG)算法等。

6.2 变间隔递阶多新息递推梯度算法

6.2.1 损失数据系统

对于线性回归损失数据系统的变间隔递阶辨识模型(110)和(118),考虑从ts－p＋1到ts的可得到的最新p组数据,定义堆积输出向量Y(p,ts)和Yi(p,ts),堆积信息矩阵Φ(p,ts)和子信息矩阵Φi(p,ts)如下:

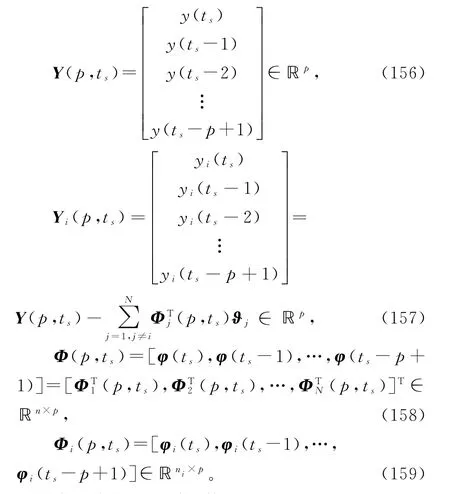
定义多新息准则函数为

定义堆积输出信息向量Zi,t和堆积信息矩阵Ωi,t如下:

则准则函数J7i(ϑi)可以写为

求准则函数J7i(ϑi)对参数向量ϑ的一阶偏导数,可以得到准则函数J7i(ϑi)的梯度向量

令(ts)∈ℝn表示参数向量ϑi在时刻ts的递推估计。在ϑi＝(ts－1)点的梯度为

设μi(ts)≥0为收敛因子。根据负梯度搜索,极小化准则函数J7i(ϑi),可以得到下列梯度递推关系:

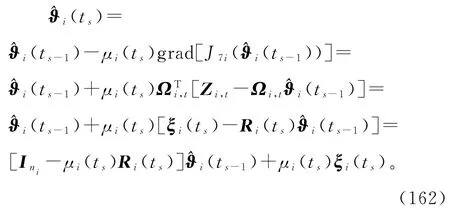
式(162)可以看作状态为(ts),输入为μi(ts)ξi(ts)的离散时间系统,为了保证参数估计向量(ts)收敛,要求矩阵[Ini－μi(ts)Ri(ts)]的特征值均在单位圆内,且单位圆上没有重特征值,即(ts)必须满足－Ini≤Ini－μi(ts)Ri(ts)≤Ini,故收敛因子μi(ts)的一个保守选择是

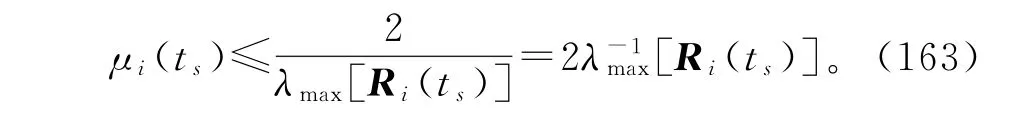
由于特征值计算很复杂,故收敛因子也可简单取为

由于式(160)右边包含了未知关联参数ϑj(j≠i),应用递阶辨识原理,用它们前一时刻的估计(ts－1)代替,得到

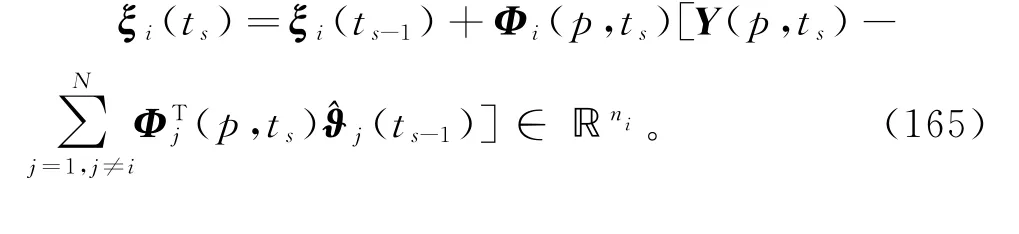
取μi(ts)＝1/ri(ts),ri(ts)＝tr[Ri(ts)]＝ri(ts－1)＋‖φi(ts)‖2,ri(t0)＝1或ri(t0)＝0时,联立式(162),(165),(161),(156)～(159),便得到辨识线性回归损失数据系统(1)参数向量ϑi的变间隔递阶多新息递推梯度算法,简称变间隔递阶多新息梯度算法(interval-varying hierarchical multi-innovation gradient algorithm,V-HMIG 算法):

读者可以写出引入收敛指数、遗忘因子后的变间隔递阶多新息梯度算法。

6.2.2 稀少量测数据系统

对于稀少量测数据系统,假设可得到的观测数据为y(ts)和φ(ts),s＝1,2,3,…。设正整数p为新息长度。

对于线性回归稀少量测数据系统的变间隔递阶辨识模型(110)和(118),考虑从ts－p＋1到ts的可得到的最新p组数据,定义堆积输出向量Y(p,ts)和Yi(p,ts),堆积信息矩阵Φ(p,ts)和子信息矩阵Φi(p,ts)如下:

仿照线性回归损失数据系统(1)的V-HMIG 算法的推导,可以得到辨识线性回归稀少量测数据系统(1)参数向量ϑi的变间隔递阶多新息梯度算法(V-HMIG 算法):

在变间隔递阶多新息梯度辨识算法(180)～(189)中引入收敛指数、加权因子、遗忘因子,便得到变间隔修正递阶多新息梯度(V-M-HMIG)算法、变间隔加权递阶多新息梯度(V-W-HMIG)算法、变间隔遗忘因子递阶多新息梯度(V-FF-HMIG)算法、变间隔加权修正递阶多新息梯度(V-W-M-HMIG)算法、变间隔遗忘因子修正递阶多新息梯度(V-FFM-HMIG)算法、变间隔加权遗忘因子递阶多新息梯度(V-W-FF-HMIG)算法、变间隔加权遗忘因子修正递阶多新息梯度(V-W-FF-M-HMIG)算法等。

变间隔多新息梯度类辨识方法、变间隔递阶多新息梯度类辨识方法也是首次在此提出的。它可以发展为FIR 模型和CAR 模型的变间隔多新息梯度算法、以及(自回归)输出误差系统的变间隔辅助模型多新息梯度(V-AM-MIG)算法、变间隔辅助模型递阶多新息梯度(V-AM-HMIG)算法等。

7 变间隔递阶最小二乘辨识方法

7.1 变间隔最小二乘辨识算法

对于线性回归辨识模型(1),定义和极小化准则函数

可以得到辨识系统(1)参数向量ϑ的递推最小二乘算法(RLS算法)如下:

在数据缺失情形,假设可得到的观测数据为y(ts)和φ(ts),s＝0,1,2,…,不可得到的数据为y(ts＋i)和φ(ts＋i),i＝1,2,…,－1,此时RLS算法(190)～(193)不可实现。如果用ts代替式(190)～(193)中的t得到

从s＝0,1,2,…的递推计算过程看,这个算法也不可实现,因为当＞1时,式(194)～(197)右边存在未知量(ts－1)和P(ts－1)。一个办法是用ts代替式(1)中的t,得到一个新的辨识模型

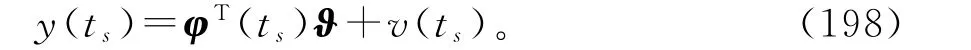
对于变间隔辨识模型(198),定义随时间s递增的准则函数为

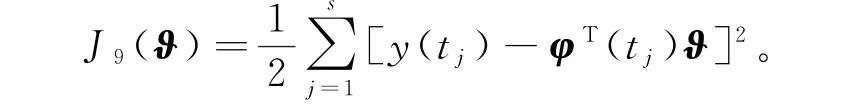
极小化准则函数J9(ϑ),可以得到辨识系统(1)参数向量ϑ变间隔递推最小二乘算法(interval-varying RLS algorithm,V-RLS算法):

借助增益向量L(ts)＝P(ts)φ(ts)∈ℝn,VRLS算法可等价表示为

在初始条件(t0)＝1n/p0和P(t0)＝p0In下,利用可得到的观测信息y(ts)和φ(ts),V-RLS算法(201)～(204)可以递推计算参数估计向量(ts),在数据不可得到时,参数估计保持不变,即

可以在变间隔递推最小二乘算法中引入加权因子、遗忘因子,得到变间隔加权递推最小二乘(V-WRLS)算法、变间隔遗忘因子递推最小二乘(V-FFRLS)算法。

7.2 变间隔递阶最小二乘算法

用ts代替式(2)和(3)中的t,得到变间隔递阶辨识模型:

可得到的观测是y(ts)和φ(ts)及其分量φi(ts),而虚拟子系统的输出yi(ts)是未知的,

故将式(207)中yi(ts)代入式(209)得到

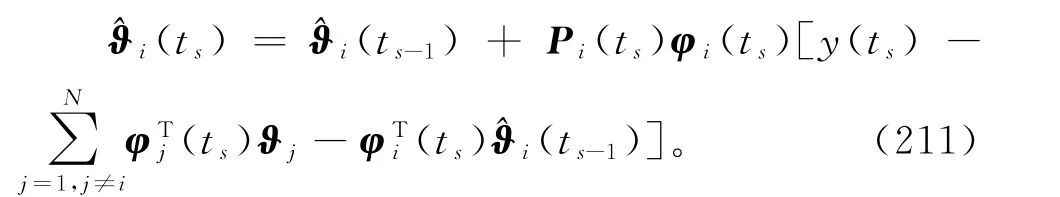
式(211)右边包含了其它子系统的未知子参数向量ϑj(j≠i),所以算法(210)～(211)无法实现。为了实现参数估计(ts)的递推计算,根据递阶辨识原理进行关联项的协调,式(211)中未知的ϑj用它在前一时刻t＝ts－1的估计(ts－1)代替,可得

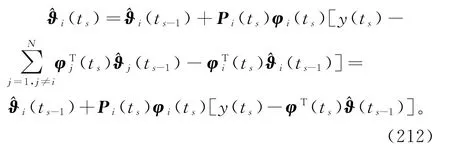
式(212)和式(210)构成了估计子参数向量ϑi的变间隔递阶最小二乘算法(interval-varying hierarchical least squares algorithm,V-HLS算法):

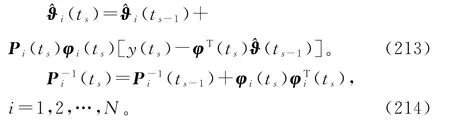
定义增益向量(t)＝(ts),t＝ts,ts＋1,…,ts＋1－1,将矩阵求逆引理应用到式(214),V-HLS算法可以等价表示为

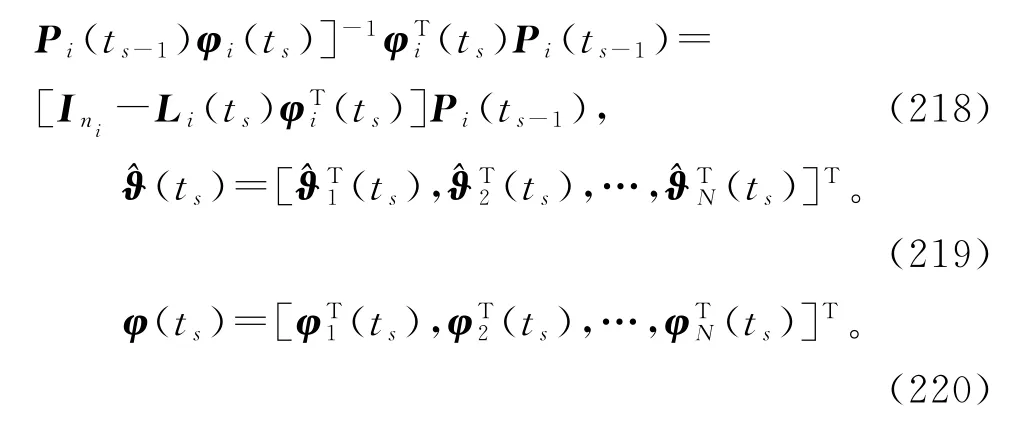
定义块对角协方差阵(block diagonal covariance matrix)

于是,估计线性回归系统(1)参数向量ϑ的变间隔递阶最小二乘算法(215)～(220)可以等价表示为

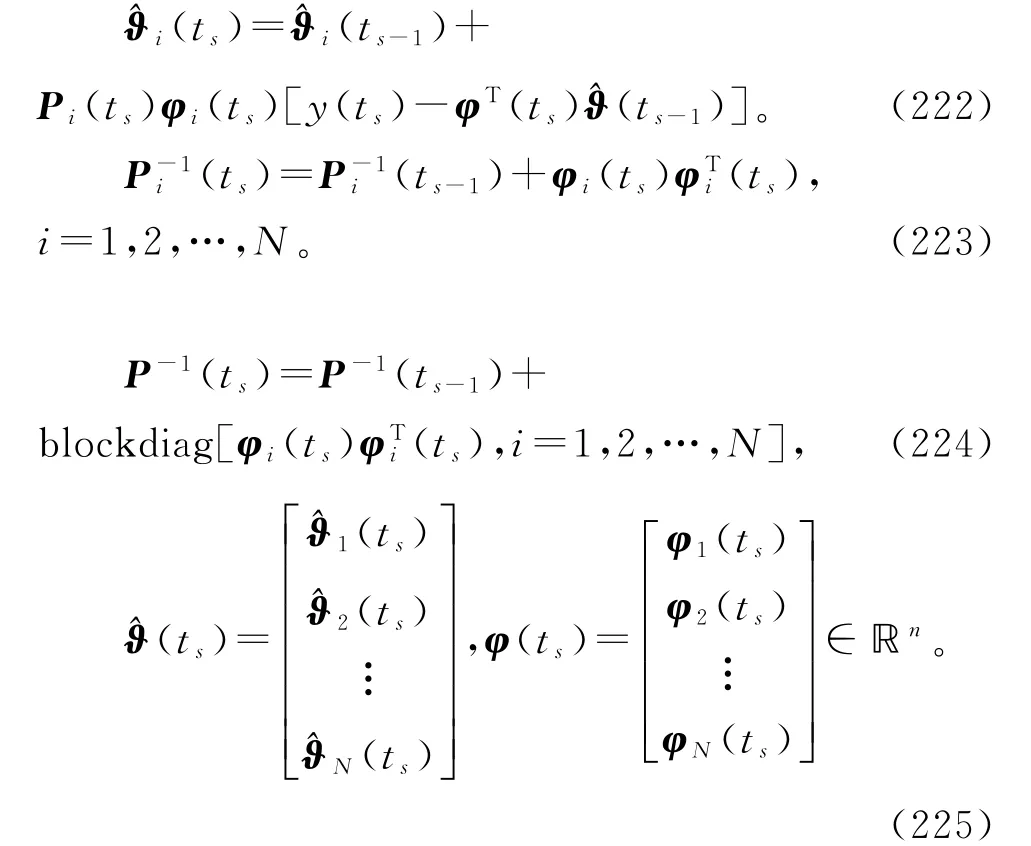
可以在变间隔递阶最小二乘算法中引入加权因子、遗忘因子,得到变间隔加权递阶最小二乘(V-WHLS)算法、变间隔遗忘因子递阶最小二乘(V-FFHLS)算法。

8 变间隔递阶多新息最小二乘方法

这里针对损失数据系统和稀少量测数据系统,讨论变间隔多新息最小二乘辨识方法、变间隔递阶多新息最小二乘辨识方法。

8.1 变间隔多新息最小二乘辨识算法

8.1.1 损失数据系统

令正整数p为新息长度。对于损失数据系统,假设可得到的观测数据为y(ts),φ(ts),y(ts－1),φ(ts－1),y(ts－2),φ(ts－2),…,y(ts－p＋1),φ(ts－p＋1)。

根据变间隔辨识模型(198),利用可得到的观测数据定义堆积输出向量Y(p,ts)和堆积信息矩阵

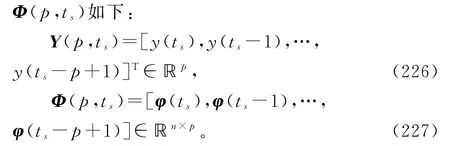
借助多新息辨识理论,基于V-RLS 辨识算法(201)～(204),将式(201)中标量新息

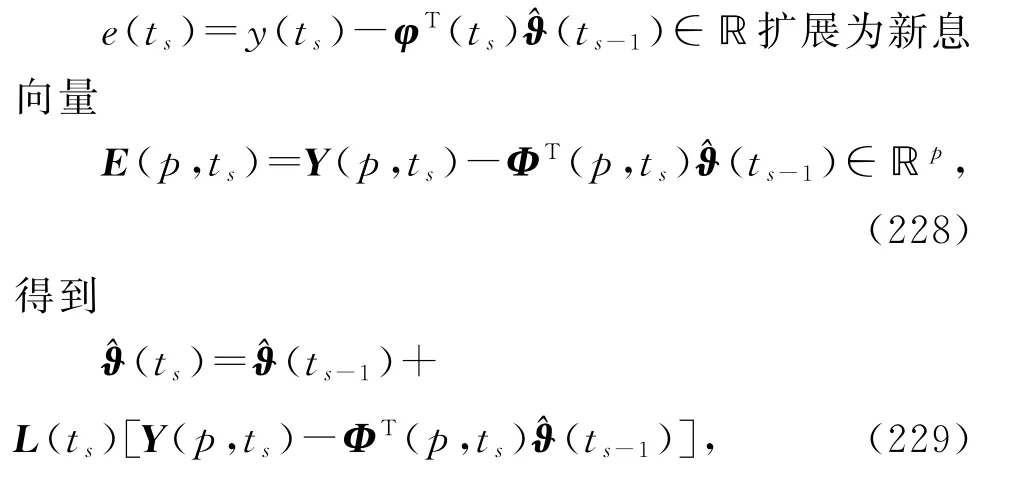
将式(202)～(203)中信息向量φ(ts)扩展为

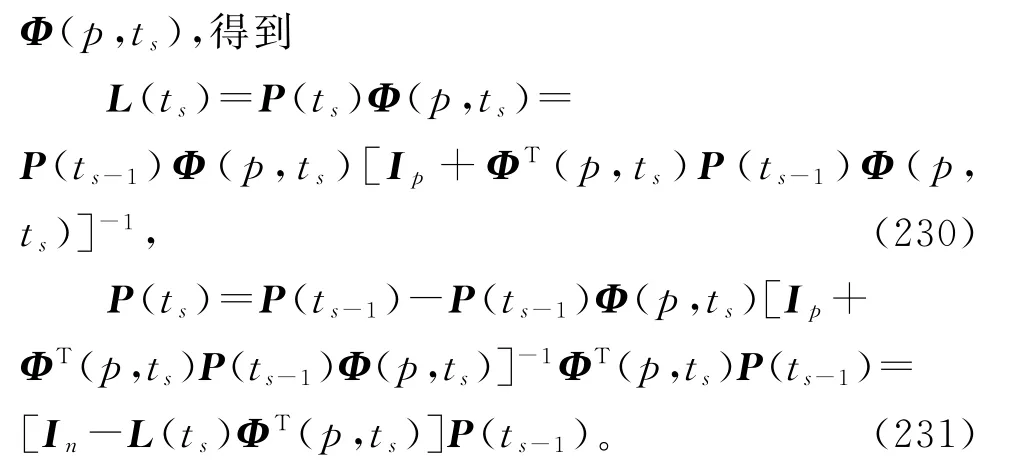
式(229)～(231)和(226)～(227)构成了辨识线性回归损失数据系统(1)参数向量ϑ的变间隔多新息最小二乘算法(interval-varying multi-innovation least squares algorithm,V-MILS算法):

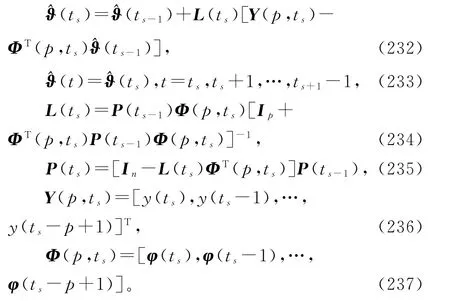
8.1.2 稀少量测数据系统

对于稀少量测数据系统,假设可得到的观测数据为y(ts)和φ(ts),s＝1,2,3,…。设正整数p为新息长度。根据变间隔辨识模型(198)和(206),利用可得到的观测数据定义堆积输出向量Y(p,ts)和堆积信息矩阵Φ(p,ts)如下:

基于V-RLS算法(201)～(204),引入新息长度(innovation length),仿照线性回归损失数据系统的V-MILS算法(232)～(237)的推导,可以得到辨识线性回归稀少量测数据系统(1)参数向量ϑ的变间隔多新息最小二乘算法(V-MILS算法):

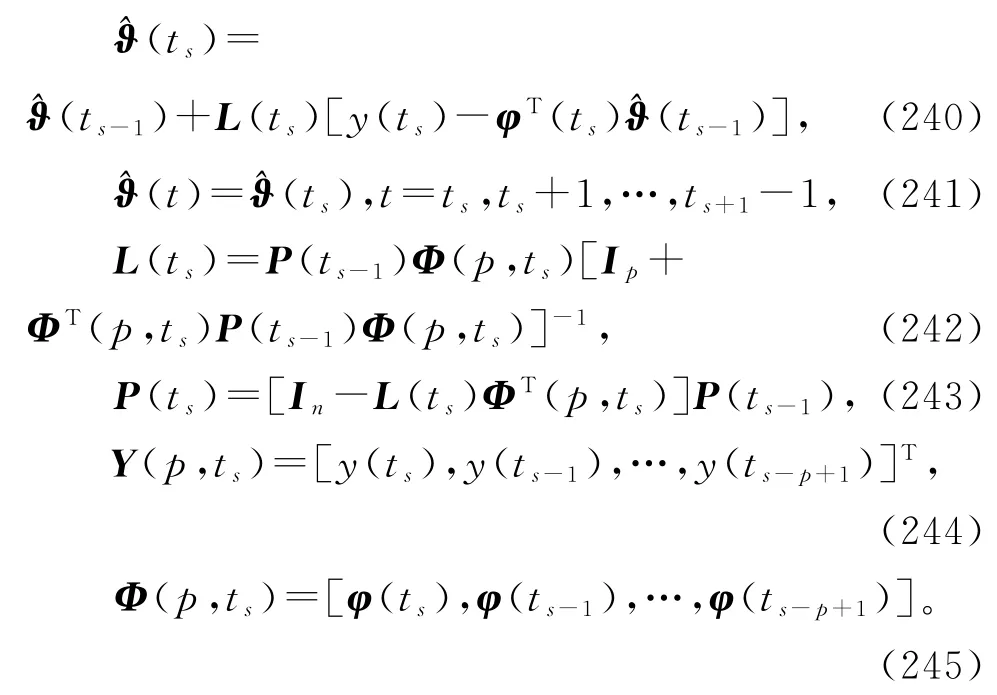
当新息长度p＝1时,V-MILS辨识算法退化为V-RLS辨识算法(201)～(204)。

可以在V-MILS 算法中引入加权矩阵Ws∈ℝp×p≥0,引入遗忘因子0＜λ≤1,得到变间隔加权多新息最小二乘(V-W-MILS)算法、变间隔遗忘因子多新息最小二乘(V-FF-MILS)算法和变间隔加权遗忘因子多新息最小二乘(V-W-FF-MILS)算法。

8.2 变间隔递阶多新息最小二乘算法

8.2.1 损失数据系统

对于多新息辨识算法,令正整数p为新息长度。对于损失数据系统,假设可得到的观测数据为

根据辨识模型(198)和(206),利用可得到的观测数据定义堆积输出向量Y(p,ts),堆积信息矩阵Φ(p,ts)和堆积子信息矩阵Φi(p,ts)如下:

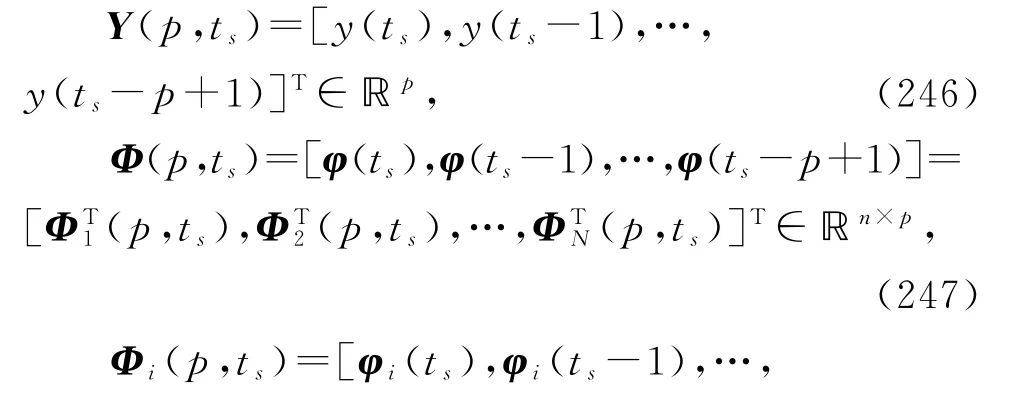
借助多新息辨识理论,基于变间隔递阶最小二乘算法(215)～(220),将式(215)中标量新息

式(250)～(252)和(246)～(248)构成了辨识线性回归损失数据系统(1)参数向量ϑ的变间隔递阶多新息最小二乘算法(interval-varying hierarchical multi-innovation least squares algorithm,V-HMILS算法):

8.2.2 稀少量测数据系统

对于稀少量测数据系统,假设可得到的观测数据为y(ts)和φ(ts),s＝1,2,3,…。设正整数p为新息长度。根据辨识模型(198)和(206),利用可得到的观测数据定义堆积输出向量Y(p,ts),堆积信息矩阵Φ(p,ts)和堆积子信息矩阵Φi(p,ts)如下:

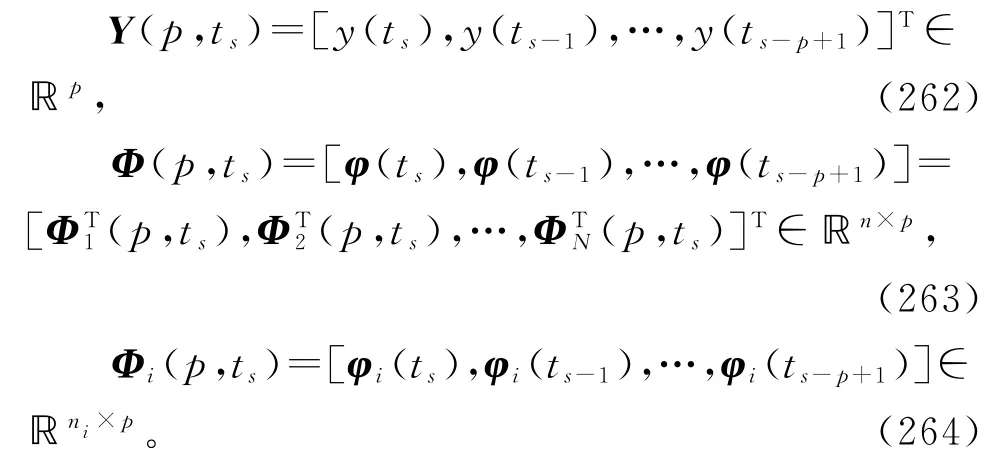
基于V-HLS算法(215)～(220),引入新息长度(innovation length),仿照线性回归损失数据系统的V-MILS算法(253)～(261)的推导,可以得到辨识线性回归稀少量测数据系统(1)参数向量ϑ的变间隔递阶多新息最小二乘算法(V-HMILS算法):

可以在V-HMILS算法中引入加权矩阵Ws∈ℝp×p≥0,引入遗忘因子0＜λ≤1,得到变间隔加权递阶多新息最小二乘(V-W-HMILS)算法、变间隔遗忘因子递阶多新息最小二乘(V-FF-HMILS)算法、变间隔加权遗忘因子递阶多新息最小二乘(VW-FF-HMILS)算法。

当新息长度p＝1时,V-HMILS辨识算法退化为V-HLS辨识算法(215)～(220)。当子系统数目N＝1时,V-HMILS算法退化为V-RLS算法(201)～(204)。当新息长度p＝1,子系统数目N时,V-HMILS算法退化为RLS算法(190)～(193)。

V-HMILS算法(265)～(273)随s增加计算参数估计的步骤如下。

2)采集观测数据y(t)和φ(t)。

3)如果观测数据y(t)和φ(t)可得到,就跳到下一步;否则置(t)＝(ts),t增加1,即t＝t＋1,转到步骤2)。

4)置s＝s＋1,ts＝t,＝ts－ts－1,用式(269)构造堆积输出向量Y(p,ts),用式(270)构造堆积信息矩阵Φ(p,ts)。从式(272)的φ(ts)中读出子信息向量φi(ts),用式(271)构造堆积信息矩阵Φi(p,ts),i＝1,2,…,N。

5)用式(267)计算增益矩阵Li(ts),用式(268)计算协方差阵Pi(ts),i＝1,2,…,N。

6)用式(265)刷新参数估计向量(ts),i＝1,2,…,N,根据式(273)构成参数估计向量^ϑ(ts),根据式(266)令(t)＝(ts)。

7)t增加1,转到步骤2)。

9 结语

利用系统的观测输入输出数据,针对损失数据系统和稀少量测数据系统,引入变间隔概念,基于递阶辨识原理,获得系统的变间隔递阶辨识模型,针对线性回归系统,提出了变间隔递阶(多新息)随机梯度辨识方法、变间隔递阶(多新息)递推梯度辨识方法、变间隔递阶(多新息)最小二乘辨识方法等。这些变间隔递推辨识方法可以推广到有色噪声干扰下的线性和非线性损失数据随机系统和稀少量测数据随机系统中[35-46]。