射影空间上涉及q,c阶差分算子的第二基本定理
2018-01-16,
,
(上海理工大学 理学院,上海 200093)
1 问题的提出
Nevanlinna[1]在1925年建立了复平面上关于亚纯函数的第二基本定理.Cartan[2]将其推广到复射影空间n()中全纯曲线上,得到了相应的第二基本定理.Huang等[3]证明了Nevanlinna第二基本定理在复平面上更一般的形式,见定理1。
定理1设函数f在复平面上非常值亚纯,a1,…,aq是q个互不相同的复数,则对于任给的ε>0有
(1)
式中,Nram,f(r)=Nf′(r,0)+2Nf(r,)-Nf′(r,),r→且r∉E,这里E⊂(0,)是一个对数测度为有穷的集合.
后来,Wong[4]将这一经典理论推广到了高维的情况(更多的拓展参见文献[5-7]),得到如下定理.
定理2[4]设f:→n是一个线性非退化的全纯映射,H1,…,Hq是q个处于一般位置的超平面,则
式中,Nram,f(r)=N(r,W(f)=0)是f的朗斯基行列式零点的计数函数.S(r,f)=o(T(r,f)),r→且r∉E,这里E⊂(0,+)是一个对数测度为有穷的集合.
2006年,Halburd等[8]考虑用差分算子Δcf=f(z+c)-f(z)≢0来替代f′,得到了涉及差分算子所对应的情形.
定理3[8]设f是复平面上的有穷级亚纯函数,满足Δcf=f(z+c)-f(z)≢0,其中c≠0是常数,则对于q个互异的点a1,…,aq∈∪{}有
其中
定理4[9]设f:→n是一个有穷级的全纯映射,且f()⊄Hi,i=1,…,q,这里H1,…,Hq是q个处于一般位置的超平面.若WΔc(f)≢0,其中c≠0是常数,则
式中,NΔc(r)=N(r,WΔc(f)=0).
受此启发,考虑如下的q,c阶差分算子Δq,cf=f(qz+c)-f(z),其中q∈{0},c∈,并将定理4作如下推广,得到定理5.
定理5设f:→n是一个零级全纯映射,并且f()⊄Hi,i=1,…,q,H1,…,Hq是q个处于一般位置的超平面.若WΔq,c(f)≢0,q∈{0},c∈,则对任给的ε>0有
式中,NΔq,c(r)=N(r,WΔq,c(f)=0).
2 引理及证明
引理1(Nevanlinna第一基本定理)设f:→n是亚纯映射,且f()⊄H,这里H是处于一般位置的超平面,则
mf(r,H)+Nf(r,H)=Tf(r) (r>1)
引理2[10]设f是零级的亚纯函数,q∈{0},c∈,则
引理3设f是零级的亚纯函数,q∈{0},c∈,则
且T(r,qz+c)=T(r,f(z))+S(r,f).
定义1设f:→n()是全纯映射,是f的既约表示,其中f0,f1,…,fn是无公共零点的全纯函数.记H={[w0,…,wn]∈n(其中是n+1上的非零表示.当≢0时,记
类似于文献[10]中的定义,则有
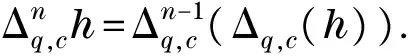
定义3设f:→n()是全纯映射,是f的既约表示,是n+1上的非零表示,与分担是指=0当且仅当若与有相同的零点和重数,则称与分担
引理4[11](转换律) 设f:→n是一个全纯映射,是f的一个既约表示,φ是n上的一个自同构,则
WΔq,c(φ∘f)=cφWΔq,c(f)
其中,
q∈{0},c∈

证明记
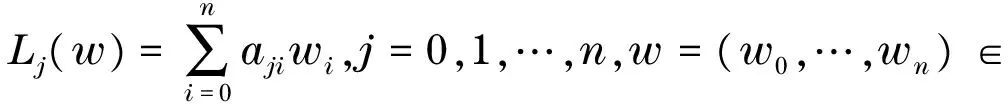
WΔq,c(φ∘f)=
WΔq,c(f)detφ*=WΔq,c(f)cφ
于是引理4得证.
引理5设H1,…,Hq是n()上q个处于一般位置的超平面,记T为所有单射μ:{0,1,…,n}→{1,…,q}的集合,则有
类似于文献[10]中定理A3.1.3,则有
引理6设f=[f0,…,fn]:→n()是零级的全纯曲线,H1,…,Hq是n()上任意q个超平面,且使得f()⊄Hi,i=1,…,q.设K⊂{1,…,q},使得是Hj(1≤j≤q)的系数)线性无关.则
r→且r∉E,这里E⊂(0,)是一个对数测度为有穷的集合.
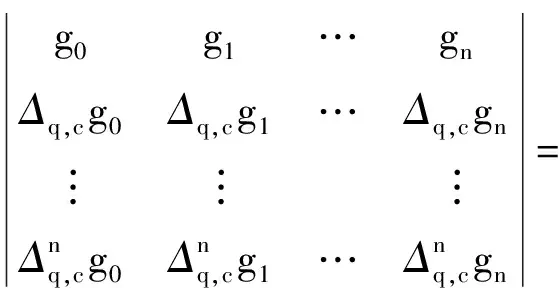
证明设H1,…,Hq是n+1上的超平面,不失一般性,q≥n+1,#K=n+1.记T是所有使得线性无关的单射μ:{0,1,…,n}→{1,…,q}的集合.则
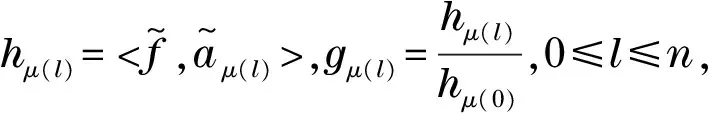
其中
结合引理2和引理3可知
故
S(r,f).
且
所以
I1≤S(r,f)
又
由引理4可得
C|WΔq,c(f0,…,fn)|
这里C≠0是常数,则
结合I1,I2,从而引理6可证.
3 定理5的证明
结合引理5和引理6可得
两式相加可得
于是定理得证.
推论设f:→n是一个零级全纯映射,并且f()⊄Hi,i=1,…,q,H1,…,Hq是q个处于一般位置的超平面,f与Δq,cfCM分担Hj.若q≥N+2,则WΔq,c(f)≡0.
证明倘若不然,可假设WΔq,c(f)≡0.由定理5可得
结合第一基本定理得
设z0∈,
所以(q-n-1)Tf(r)≤0.又q>N+2,故得出矛盾.
因此
WΔq,c(f)≡0.
[1] NEVANLINNA R.Zur theorie der meromorphen funktionen[J].Acta Mathematica,1925,46(1):1-99.
[2] CARTAN H.Sur les systèmes de fonctions holomorphes à variétés linéaires lacunaires et leurs applications [J].Annales Scientifiques de l′École Normale Supérieure,1928,45(3):255-346.
[3] HUANG Y T,WONG P M.Prediction of reservoir permeability using genetic algorithms [J].IEEE International Fuzzy Systems Conference,1999 ,3 (3):1528-1533.
[4] WONG P M,STOLL W.Second main theorem of Nevalinna theory for non-equidimensional meromorphic maps[J].American Journal of Mathematics,1994,116(5):1031-1071.
[5] WONG P M.On the Second Main Theorem of Nevanlinna theory[J].American Journal of Mathematics,1989,111(4):549-583.
[6] WONG P M.Applications of Nevanlinna theory to geometric problems[C]∥Proceedings of the 3rd International Conference of Chinese Mathematicians.Hong Kong,China:The Chinese University of Hong Kong,2004:523-594.
[7] WONG P P M,Wong P W.The second main theorem on generalized parabolic manifolds[M]∥ESCASSUT A,TUTSCHKE W,YANG C C.Some Topics on Value Distribution and Differentiability in Complex and P-Adic Analysis.Beijing:Science Press,2008:1-41.
[8] HALBURD R G,KORHONEN R J.Nevanlinna theory for the difference operator[J].Annales-Academiae Scientiarum Fennicae Mathematica,2006,31(2):463-478.
[9] HALBURD R G,KORHONEN R J.Existence of finite-order meromorphic solutions as a detector of integrability in difference equations[J].Physica D:Nonlinear Phenomena,2006,218(2):191-203.
[10] RU M.Nevanlinna theory and its relation to Diophantine approximation [M].River Edge,NJ:World Scientific,2001.
[11] PIT-MANN W,HIU-FAI L,WONG P P.A Second Main Theorem on P~n for difference operator[J].Science in China,2009(12):2751-2758.
