多车次同时送取货物车辆路径问题的量子蚁群算法

,

(1.上海理工大学 管理学院,上海 200093; 2.国网上海市电力公司物资公司,上海 200002)

1 研究背景

同时送取货物的车辆路径问题(vehicle routing problem with simultaneous deliveries and pickups,VRPSDP)最早由Min[1]于1989年提出,Dethloff[2]于2001年首次从逆向物流的角度研究了此问题.VRPSDP是逆向物流车辆路径问题(vehicle routing problem,VRP)的一个重要组成部分,与其并列的还有先送货后取货的车辆路径问题(vehicle routing problem with backhauls,VRPB),以及混合送货和取货的车辆路径问题VRPBM(vehicle routing problem with backhauls of mixed loads,VRPBM)[3].

由于VRPSDP将正向物流和逆向物流同时加以考虑,更接近于现实生活中的物流配送服务,对实际问题更有指导意义,近年来越来越多的学者对VRPSDP展开了研究[3-9],其研究成果可被分为两大部分:a.对基本VRPSDP进行改进,提出了多种VRPSDP的变种问题,如带时间窗的VRPSDP[4]、具有车辆最大行程约束的VRPSDP[5]、随机旅行时间的VRPSDP[3]、车辆容量可调节的VRPSDP[6]、异车型VRPSDP等[7].b.设计并提出了多种求解VRPSDP的方法.张建勇等[8]结合2-opt 法和等级替换策略设计了求解VRPSDP 的一种混合遗传算法,给出了该算法初始种群的两种生成规则,阐述了违反约束条件的处理方法;Liu等[4]在求解带时间窗的VRPSDP时,用遗传算法进行局部搜索,用禁忌搜索进行路径分配的优化;吴斌等[9]提出了基于混沌理论的精英均值计算旋转角算法;Qu等[6]设计了两阶段启发式算法,并将其用于车辆容量可调节的VRPSDP.

自VRPSDP 提出至今,其模型的改进和求解算法虽然均已取得很大研究成果,但大部分研究仍存在一些不足,可归纳为两方面.一方面,绝大多数VRPSDP模型假设在计划期内(一般为一天)配送车辆只能运行一次,考虑多车次的VRPSDP模型在现有文献中极其罕见.然而,现实生活中,物流公司为了节约配送成本和完成配送任务,通常会启用较少的配送车辆,同一辆车会多次往返于配送中心,完成多条配送路线的配送任务.另一方面,绝大多数VRPSDP模型没有考虑货物的装卸时间和车辆的工作时间.

本文研究多车次同时送取货的车辆路径问题(multi-trip vehicle routing problem with simultaneous deliveries and pickups,MTVRPSDP),并在该问题中考虑了货物的装卸时间、车辆的工作时间和载重量限制.与基本VRPSDP相比,本文考虑的MTVRPSDP存在以下几个难点:第一,多车次的引入,增加了问题的复杂度;第二,对车辆工作时间的限制,加强了问题的约束.当车辆工作时间接近最大限制时,即使车辆的载重量仍然可以满足某些客户的需求,但也必须返回配送中心.对车辆工作时间的限制不仅会导致车辆总行程的增加,而且会导致车辆数和配送路径数的增加,使问题的优化难度加大[3].

为了求解MTVRPSDP,本文在量子计算和蚁群算法的基础上,吸收这两种方法的长处和优势,克服它们的短处和缺陷,进而提出求解该问题的量子蚁群算法.本文的第二部分建立了MTVRPSDP问题的数学模型;第三部分介绍了量子蚁群算法,以及求解MTVRPSDP的基本流程;第四部分进行了实例仿真,采用量子蚁群算法求解MTVRPSDP问题,获得了满意的结果.

2 MTVRPSDP描述及其数学模型

2.1 问题描述

本文研究的MTVRPSDP是在所有客户点的位置和货物需求均已知的情况下,完成所有客户的配送和取货服务,并要求配送中心启用的配送车辆成本和完成配送服务的行驶成本之和达到最小.假设每个客户点可以同时收货和发货,也可以只收货或只发货;每辆车可以在一个工作日内为多条配送路线上的客户提供送货和取货服务.此外,配送车辆和客户点还必须同时满足如下条件:

a.服务约束,每辆车可以服务多个客户,但一个客户仅能由一辆车服务;

b.配送中心约束,所有车辆由单一配送中心出发,配送完路径上所有的客户后返回配送中心;

c.装载量约束,每条配送路径上车辆的装载量不能超过其最大载重量限制;

d.最大工作时间限制,每辆车的工作时间(行驶时间和装卸货时间之和)不能超过其最大工作时间.

2.2 符号定义与数学模型

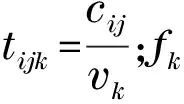
决策变量:

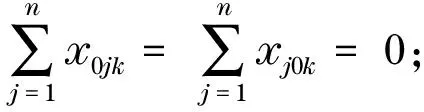
MTVRPSDP的目标是在满足上述约束条件的基础上,确定完成所有送货和取货任务且期望成本最小的车辆路径.可将MTVRPSPD表述为如下数学模型:

目标函数

(1)

约束条件

(2)

(3)

(4)

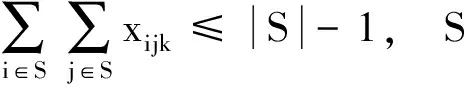
(5)

(6)

0≤qijkxijk≤Gk,i∈V,j∈V,k∈K

(7)

(8)

xijk∈{0,1},i∈V,j∈V,k∈K

(9)

其中:目标函数式(1)表示最小化所有车辆的启动成本与行驶路径成本之和;约束式(2)保证每个顾客都要被服务一次且仅被服务一次;式(3)保证一辆车服务客户j,则离开该客户的仍然是这辆车,即客户j只被同一辆车服务;式(4)保证每辆车从配送中心出发并最终返回到配送中心;式(5)排除子回路;式(6)表示车辆在经过客户j前后的载货量变化情况;式(7)保证每辆车在任意一条配送路段上的货物运输量不超过其最大载重量,且不为负;式(8)保证车辆k在计划期内的总工作时间不超过其最大工作时间Tk,stki表示车辆k在节点i的装卸时间;式(9)是决策变量xijk的取值范围.

3 MTVRPSDP的量子蚁群算法

蚁群算法(ant colony optimization,ACO)是意大利学者Dorigo等[10]通过模拟蚁群觅食行为提出的一种基于种群的模拟进化算法,其在求解组合优化难题和连续优化问题中均取得了较好的结果.近年来,越来越多的学者利用ACO求解物流配送中的车辆调度和路径优化问题[11].相比于其他智能优化算法,ACO具有较强鲁棒性、易与其他方法结合的优点.首先,ACO对初始路线的要求不高,即ACO的求解结果不依赖于初始路线的选择,而且在搜索过程中不需要进行人工调整;其次,ACO的参数数目少,设置简单.但是,ACO也有一些不足之处,如:容易陷入局部最优,搜索速度比较慢等.

蚂蚁状态的转移和路径上信息素的更新是ACO的重要组成部分.本文针对基本ACO收敛速度慢和易陷入局部最优等缺点,将量子进化算法中的量子比特和量子旋转门引入ACO,用以改进基本ACO算法中的状态转移概率,有效抑制算法的早熟现象,并加快算法的求解速度.本文将改进后的ACO算法称为量子蚁群算法(quantum ant colony optimization,QACO),并将其用于求解MTVRPSDP.

3.1 量子编码特性

量子计算的基本原理是使量子态所处叠加态的各个基态间的相对相位和概率幅度发生改变,使各个基态的发生概率产生变化,从而使其叠加态发生变化,具有并行、叠加、干涉等特征[12].量子比特是量子计算中基本信息的存储单元,采用|0〉和|1〉(“|〉”称为Dirac记号,在量子力学中表示状态)来表示微观粒子的两种基本状态.单量子比特的任意状态都可以表示为这两个基本状态的线性组合,即除|0〉和|1〉之外,还可以是这两种状态之间的中间状态(叠加态):|φ〉=α|0〉+β|1〉(α和β是一对复数,表示量子态的概率幅,即量子态|φ〉以|α|2的概率坍缩到|0〉或以|β|2的概率坍缩到|1〉,且满足|α|2+|β|2=1).

一个量子比特同时可包含0和1的信息,那么一个长度为m的量子位可以表示2m种不同的状态,有m个量子位的个体j的概率幅可表示为

(10)

其中,|αi|2+|βi|2=1(i=1,2,…,m).

在QACO中用量子比特来表示量子信息素,设种群大小为n,其量子信息素用量子位表示为p=(p1,p2,…,pn),其中pj(j=1,2,…,n)如式(10)所示.

3.2 量子旋转门

量子比特相位的改变可以用量子旋转门实现,量子旋转门的调整方式可定义为:

(11)

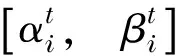
本文针对MTVRPSDP的求解和借鉴文献[12]中量子旋转角的取值方法,设计了一种改进的θi取值方法,该方法能够根据当前量子比特概率幅和MTVRPSDP问题的目标函数值计算出相位的旋转角度,从而实现蚁群算法中种群的多样性,避免算法早熟收敛.θi的取值定义如下:

θi=s(αiβi)(θ0+sign(f(xi)-f(bi))0.07π)

(12)

式中,s(αiβi)控制旋转角的旋转方向,若αiβi≥0,s(αiβi)=1,否则,s(αiβi)=-1.sign(f(xi)-f(bi))为符号函数,自适应地调整旋转角的大小.当f(xi)-f(bi)>0时,sign(f(xi)-f(bi))=1;当f(xi)-f(bi)<0时,sign(f(xi)-f(bi))=-1;当f(xi)-f(bi)=0时,则sign(f(xi)-f(bi))=0.θ0为初始旋转角度,xi表示当前解,bi表示当前最优解,f(x)为目标函数.

3.3 状态转移规则

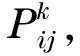
(13)

蚂蚁k由客户点i出发,采用伪随机规则确定所要访问的下一个客户:若q>q0(q0∈(0,1)是一个常数;q为(0,1)区间的随机数),根据式(13)计算出的转移概率并按照轮盘赌的方法确定下一个访问的客户;否则,取转移概率最大的客户j为下一个访问的客户.

3.4 信息素更新

本文利用式(14)～(16)对客户i和j路径上的信息素进行更新:

τij=(1-ρ)τij+Δτij

(14)

(15)

(16)

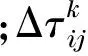
3.5 算法步骤

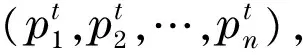
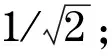
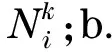
步骤3所有客户服务结束后,蚂蚁k完成一次周游,得到问题的一个可行解.更新蚂蚁数k=k+1,若k≤Num,转步骤2;否则,转步骤4.

步骤4计算各蚂蚁的目标函数值zk(k=1,2,…,Num),并记录当前最满意的解.

步骤5根据信息素更新规则,利用式(14)～(16)对信息素进行更新.

步骤6应用量子旋转门对所有客户点的量子信息进行更新.

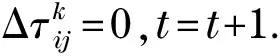
步骤8若迭代次数t

步骤9输出当前最优解.

4 算例分析

本文采用文献[14]的算例测试QACO的优化性能和MTVRPSDP模型(1)～(9)的可行性与实用性.该算例为:某第三方物流企业需要利用一定数量的车辆和配送人员为100个客户提供同时送货和取货的服务,配送中心(用0表示)的位置坐标为(34,36)(单位km),配送中心的送货需求量di和取货需求量gi均为0 t;100个客户的位置坐标,送货需求量和取货需求量如表1所示(见下页);配送中心提供的配送车辆的车型相同,平均运行速度均为35 km/h,最大装载容量均为10 t,最长工作时间均为8 h.

利用Matlab R2010a 对基本ACO和QACO算法进行编程实现,2种算法在Intel Core i5 3.40 GHz,4 GB内存,操作系统为Windows7的环境下运行.

为了确保算法之间的可比性,使基本ACO和QACO在相同的起点上进行比较,根据文献[14]对ACO和QACO的共同参数设定了相同的值:蚂蚁数Num=60,距离成本系数fk=10元/km,车辆启动成本系数hk=2 500元,客户点的装卸时间sti=0.1h,配送中心的装货(卸货)时间st0=0.1h,信息素轨迹的相对重要性α=1,能见度的相对重要性β=1,量子信息强度的相对重要性μ=2,送取货物差值的重要性λ=2,节省量的重要性ξ=1.5,信息素总量Q=15,算法迭代次数tmax=200.量子蚁群算法中的初始旋转角度θ0=0.06π.QACO算法和基本ACO算法各随机运行10次,求解结果如表2所示(见下页).基本ACO算法求出的车辆数为5,车辆行驶成本为12 047元,总成本为24 547元.QACO算法求出的车辆数也为5,车辆行驶成本为9 285.4元,总成本为21 785.4元.QACO求解结果的标准差为0.67,小于ACO求解结果的标准差为2.29,这说明QACO的求解性能比ACO的求解性能稳定.虽然QACO与ACO求得相同的车辆数,但QACO求解的平均成本和总成本分别为22 129.8元和21 785.4元,分别小于ACO求得的平均成本24 984元和总成本24 547元.这说明本文设计的QACO算法求解MTVRPSDP的求解结果优于基本ACO算法的求解结果.

表1 客户数据Tab.1 Data of clients

表2 量子蚁群算法与蚁群算法效果比较Tab.2 Comparison of the quantum-inspired ant colony algorithm with the basic ant colony algorithm

图1为ACO和QACO算法求解满意解的总成本收敛图.由图1可知,ACO算法和QACO算法迭代100次已基本趋于收敛.虽然算法迭代开始时,ACO的计算结果优于QACO的计算结果,但迭代大约50次以后QACO的计算结果优于ACO的计算结果.此外,由于QACO中转移概率的计算和客户点量子信息的计算比ACO中的计算过程繁杂,导致QACO迭代200次的总计算时间224 s多于ACO的计算时间206 s,但QACO收敛到满意解的速度比ACO收敛到满意解的速度快.

表3给出了本文和文献[14]利用不同的模型和算法求解该算例的结果.文献[14]所建立的MTVRPSDP模型为二次规划模型,所采用的求解方法是允许不可行解的禁忌搜索法,模型和算法均与本文的模型和算法不同.将本文计算结果与文献[14]的计算结果进行对比,发现:虽然本文QACO求解式(1)～(9)获得的车辆数与文献[14]中利用允许不可行解的禁忌搜索法求解得到的车辆数相同,均为5辆车;但是,文献[14]共有10条配送路径,每辆车完成2条路线的配送任务,而本文算法求得的解共有12条配送路线,有2辆车的配送路线数为3,其余3辆车的配送路线数为2,不仅完成送货和取货任务的总行驶距离928.54 km优于文献[14]的总行驶距离940.66 km,而且车辆工作总时间37.16 h优于文献[14]的工作总时间38.88 h.本文所计算的结果提高了车辆在单位时间内完成送货和取货的任务量,即提高了车辆的服务效率.这说明本文所建立的MTVRPSDP线性整数规划模型和设计的QACO算法在实际应用中均是可行的,且有一定的优越性,能够为所求解的问题找到较好的满意解.

图1 QACO和ACO迭代趋势对比Fig.1 Comparison between the iteration convergences of QACO and ACO

表3 本文计算结果与文献[14]计算结果比较Tab.3 Comparison of results obtained in the paper with the ones shown in literature [14]

QACO求得的配送路线图如图2所示(见下页),共12条配送路线.车辆1为2条配送路线的客户提供服务,2条配送路线分别为:0-2-24-4-26-96-48-51-95-53-58-59-0;0-99-28-70-93-94-27-5-7-8-0;车辆2为2条配送路线的客户提供服务,2条配送路线分别为:0-79-1-32-84-85-66-49-77-0,0-62-17-20-40-30-76-81-75-45-44-88-80-11-0;车辆3为3条配送路线的客户提供服务,3条配送路线分别为:0-16-54-56-52-57-97-67-12-0,0-14-31-83-0,0-63-68-23-55-69-15-18-92-0;车辆4为3条配送路线的客户提供服务,3条配送路线分别为:0-36-22-78-90-86-0,0-41-98-72-21-73-100-42-0,0-37-3-25-47-60-71-0;车辆5为2条配送路线的客户提供服务,2条配送路线分别为:0-87-6-46-9-74-29-50-0,0-38-10-61-19-91-43-89-13-39-34-64-65-35-0.

图2 配送方案路径图Fig.2 Distribution routes

5 结 论

MTVRPSDP的研究对物流公司的配送服务具有十分重要的现实意义.根据现实生活中配送车辆具有工作时间和载重量限制的特点,本文建立了更符合实际应用且考虑了装卸货物时间的MTVRPSDP线性整数规划模型.然后,将量子计算中的量子比特和量子旋转门引入ACO,在每个客户点设置了量子信息,用其改进蚂蚁的状态转移规则,设计了求解该问题的QACO算法.求解测试算例表明:本文所设计的MTVRPSDP线性整数规划模型在实际应用中是可行和有效的;此外,本文所设计的QACO算法能够有效求解MTVRPSDP的线性整数规划模型,具有较高的稳定性.

本文所设计的MTVRPSDP模型并未考虑客户对送货和取货服务的时间窗的限制和满意度,也未将物流公司完成配送和取货任务所启动的车辆数、行驶路径总成本作为优化的多个目标.建立并求解带有时间窗限制的多目标多车次同时取送货物的车辆路径问题模型将是作者下一步的研究工作.

[1] MIN H.The multiple vehicle routing problem with simultaneous delivery and pick-up points[J].Transportation Research Part A:General,1989,23(5):377-386.

[2] DETHLOFF J.Vehicle routing and reverse logistics:the vehicle routing problem with simultaneous delivery and pick-up[J].OR-Spektrum,2001,23(1):79-96.

[3] 张涛,余绰娅,刘岚,等.同时送取货的随机旅行时间车辆路径问题方法[J].系统工程理论与实践,2011,31(10):1912-1920.

[4] LIU R,XIE X L,AUGUSTO V,et al.Heuristic algorithms for a vehicle routing problem with simultaneous delivery and pickup and time windows in home health care[J].European Journal of Operational Research,2013,230(3):475-486.

[5] MONTANÉ F A T,GALVO R D.A tabu search algorithm for the vehicle routing problem with simultaneous pick-up and delivery service[J].Computers & Operations Research,2006,33(3):595-619.

[6] QU Y,BARD J F.The heterogeneous pickup and delivery problem with configurable vehicle capacity[J].Transportation Research Part C:Emerging Technologies,2013,32:1-20.

[7] 田宇,伍炜勤.求解异车型同时集送问题的多属性标签算法[J].系统工程理论与实践,2015,35(1):183-190.

[8] 张建勇,李军.具有同时配送和回收需求的车辆路径问题的混合遗传算法[J].中国公路学报,2006,19(4):118-122.

[9] 吴斌,钱存华,董敏,等.具有同时集送货需求车辆路径问题的混沌量子进化算法研究[J].控制与决策,2010,25(3):383-388.

[10] DORIGO M,BONABEAU E,THERAULAZ G.Ant algorithms and stigmergy[J].Future Generation Computer Systems,2000,16(8):851-871.

[11] 李娅,王东.基于混沌扰动和邻域交换的蚁群算法求解车辆路径问题[J].计算机应用,2012,32(2):444-447.

[12] 何小锋,马良.带时间窗车辆路径问题的量子蚁群算法[J].系统工程理论与实践,2013,33(5):1255-1261.

[13] LI B B,WANG L.A hybrid quantum-inspired genetic algorithm for multiobjective flow shop scheduling[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B (Cybernetics),2007,37(3):576-591.

[14] 李建,达庆利,何瑞银.多车次同时集散货物路线问题研究[J].管理科学学报,2010,13(10):1-7.