伪单调均衡问题的一种加速投影算法
2018-01-16,
,
( 上海理工大学 管理学院,上海 200093)
1 问题的提出
均衡问题EP(f,C)[1]是:寻找点x*∈C,使对∀y∈C,下面不等式成立:
f(x*,y)≥0
(1)
式中:C∈Rn是非空闭凸集,f:C×C→R为一个双重函数,即对∀x∈C,f(x,x)=0恒成立.
当f(x,y)=〈F(x),y-x〉,其中,F:C→Rn为一个连续函数,那么,EP(f,C)就转化成变分不等式问题VI(F,C),即寻找点x*∈C,使对∀y∈C,下面不等式成立:
〈F(x*),y-x〉≥0
(2)
显然,f连续,F也连续.如果f关于x*∈C是伪单调的,则F关于x*∈C也是伪单调的.
EP(f,C)在电力市场、交通运输、经济及网络等问题中都有广泛的应用[2-5].求解EP(f,C)的方法主要有三类:a.近似点法,该方法由Martinet[6]提出并首次应用在求解VI(F,C),后来Moudafi[7]在假设映射f单调的前提下将该算法推广到求解EP(f,C);b.gap函数法[8],利用连续可微的gap函数将EP(f,C)转化为最优化问题,但是,算法的收敛性建立在f强单调的基础上;c.辅助问题原理法,Cohen[9]提出x*∈C是EP(f,C)的一个解,当且仅当x*∈C是强凸问题
的唯一解,其中,ck>0,但这需要f强单调且Lipschitz连续.随后,Antipin[10]在文献[9]的基础上,在每次迭代过程中增加一个外推步,提出了一种改进算法,具体过程如下:
式中:D是Bregman距离函数;C是一个多面凸集.
该算法减弱了f的单调性,其收敛性建立在f伪单调且Lipschitz连续的基础上.
本文借助于辅助问题原理法,结合Solodov等[11]提出的求解变分不等式的改进投影算法,运用Armijo型线搜索,通过改进投影区域,使每次迭代结果更接近均衡问题的解.在f伪单调并连续(非Lipschitz连续)的前提下,证明了算法的收敛性.
2 预备知识
定义1设C⊆Rn,f:C×C→R∪{+}是双重函数,
a.若对∀x,y∈C,∃ρ>0,使得f(x,y)+f(y,x)≤-ρ‖x-y‖2,则称f在C上是强单调的.
b.若对∀x,y∈C,f(x,y)+f(y,x)≤0,则称f在C上是单调的.
c.若对∀x,y∈C,f(x,y)≥0⟺f(y,x)≤0,则称f在C上是伪单调的.
显然,(1)⟹(2)⟹(3).
定义2若存在正常数c1,c2,使得f(x,y)+f(y,z)≥f(x,z)-c1‖x-y‖2-c2‖y-z‖2,则称f在C上Lipschitz连续.
定义3设X⊆Rn,实值函数f:X→R,
a.若对∀x,y∈X,∀λ∈[0,1],有f(λx+(1-λ)y)≤max{f(x),f(y)},则称f(x)为X上的拟凸函数.
b.若对∀x,y∈X,〈f(y),x-y〉≥0蕴涵f(x)≥f(y),或者f(x) 定义4对∀z∈C,∂2f(z,z)表示凸函数f(z,·)在z处的次梯度,其中,∂2f(z,z)满足: 引理1[12]设PC(·)是C上的投影映射,则 a.‖PC(x)-PC(y)‖≤‖x-y‖,∀x,y∈Rn; b.‖PC(x)-PC(y)‖2≤〈PC(x)-PC(y),x-y〉,∀x,y∈Rn; c.〈x-PC(x),y-PC(y)〉≤0,∀y∈C,x∈Rn; d.‖PC(x)-y‖2≤‖x-y‖2-‖PC(x)-x‖2,∀y∈C,x∈Rn; e.‖PC(x)-PC(y)‖2≤‖x-y‖2-‖PC(x)-x+y-PC(y)‖2,∀x,y∈Rn. 引理2[13]设f(x,y)关于y是Gateaux可微的,如果x*是EP(f,C)的解,即f(x*,y)≥0,∀y∈C,则x*也是变分不等式〈G(x*),y-x*〉≥0,∀y∈C的解,其中,G(x)=∂f2(x,x).进一步,如果对每个x∈C,f(x,y)关于y是伪凸的,则逆命题也成立. 基于上述的理论基础,现提出求解伪单调均衡问题的一种加速投影算法.该算法的基本思想是运用Armijo型线搜索得到一个预估点并以此构造一个超平面,进一步通过适当选择步长和减小投影域使得算法产生的序列快速收敛.现介绍具体算法. 算法1 步骤1计算 令zk=xk-γmkrk,其中,mk是使得 〈∂2f(zk,zk),rk〉≥σ‖rk‖2 的最小非负数. 步骤3令k=k+1,返回步骤1. 用SOL(f,C)表示均衡问题EP(f,C)的解集,由文献[14],若f是连续的,则SOL(f,C)是闭合集合;若f是伪单调的,则SOL(f,C)是凸集.为了证明算法1的收敛性,首先作出如下假设: A1f在C上伪单调; A2f(x,y)是C×C上的连续可微凸函数且关于y是伪凸的,∂2f(x,x)在C上是上半连续的; 根据上述假设可知,SOL(f,C)是一个闭凸集. 0∈∂2f(x,x)+NC(xk) 其中,NC(xk)是xk处的外法向锥.因此,有 〈ωk,x-xk〉≥0,∀x∈C (3) 其中,ωk∈∂2f(x,x).由于f(xk,yk)是凸函数,则 (4) 结合式(3)和式(4),又因为,f(xk,xk)=0,所以,f(xk,x)≥0对∀x∈C都成立,即xk是EP(f,C)的解. 定理2若rk≠0,则对∀k≥0,存在非负数mk使得〈∂2f(zk,zk),rk〉≥σ‖rk‖2成立. 证明假设〈∂2f(zk,zk),rk〉-σ‖rk‖2<0,即有〈F(xk-γmkrk),xk-yk〉-σ‖rk‖2<0,因为,γ∈(0,1),当m→,取极限,根据f(x,y)的连续性,可以得到〈F(xk),xk-yk〉-σ‖rk‖2≤0. 由引理2,即 f(xk,yk)+σ‖rk‖2≥0 (5) 当y=xk时, (6) (7) 证明将xk+1代入式(7)的左边,可得 由引理1和引理3可得 其中,第1个不等式由引理1得到,第2个不等式由伪单调条件得到.根据引理3,可得 ‖xk+1-x*‖2≤‖xk-x*‖2- 另一方面,由zk=xk-γmkrk,即xk-zk=γmk(xk-yk),显然,由辅助问题原理,当k→时,所以, 当j→时,则有 因为,对∀x∈C,f(x,x)=0恒成立,所以, 通过改进投影区域,给出了求解伪单调均衡问题的一种加速投影算法,由以上述证明可知,此算法不要求双重函数f是Lipschitz连续的,且在伪单调条件下是全局收敛的. [1] GIANNESSI F,MAUGERI A,PARDALOS P M.Equilibrium problems:nonsmooth optimization and variational inequality models[M].Boston,MA:Springer,2001. [2] OLIVEIRA H A E JR.Coalition formation feasibility and Nash-Cournot equilibrium problems in electricity markets:a Fuzzy ASA approach[J].Applied Soft Computing,2015,35:1-12. [3] HO W,WONG S C,YING L B.Sequential optimization aproach for the mulit-class user equilibrium problem in continus transportation system[J].Journal of Advanced Transportation,2010,38(3):323-345. [4] BOGDAN M.Applications of parametric abstract equilibrium problems in economics[J].Procedia Economics and Finance,2012,3:99-104. [5] DE CEA J,FERNNDEZ J E,V DEKOCK,et al.Solving network equilibrium problems on multimodal urban transportation networks with multiple user classes[J].Transport Reviews,2005,25(3):293-317. [6] MARTINET B.Regularization d″inéquations variationnelles par approximations successives[J].Rev Fr Inform Rech Opér,1970,4(3):154-159. [7] MOUDAFI A.Proximal point algorithm extended to equilibrium problems[J].Journal of Natural Geometry,1997,15(1/2):91-100. [8] MASTROENI G.Gap functions for equilibrium problems[J].Journal of Global Optimization,2003,27(4):411-426. [9] COHEN G.Auxiliary problem principle extended to variational inequalities[J].Journal of Optimization Theory and Applications,1988,59(2):325-333. [10] ANTIPIN A S.The convergence of proximal methods to fixed points of extremal mappings and estimates of their rate of convergence[J].Computational Mathematics and Mathematical Physics,1995,35(5):539-551. [11] SOLODOV M V,SVAITER B F.A new projection method for variational inequality problems[J].SIAM Journal on Control and Optimization,1999,37(3):765-776. [12] ANH P N,LE THI H A.An Armijo-type method for pseudomonotone equilibrium problems and its applications[J].Journal of Global Optimization,2013,57(3):803-820. [13] 徐庆,朱道立,鲁其辉.Nash均衡、变分不等式和广义均衡问题的关系[J].管理科学学报,2005,8(3):1-7. [14] KONNOV I.Combined relaxation methods for variational inequalities[J].Berlin Heidelberg:Springer,2001:77-92. [15] WANG Y J,XIU N H,WANG C Y.Unified framework of extragradient-type methods for pseudomonotone variational inequalities[J].Journal of Optimization Theory and Applications,2001,111(3):641-656.3 加速投影算法


4 收敛性分析


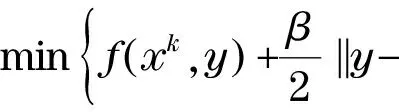



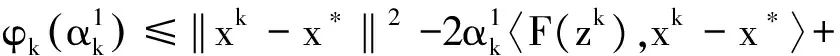
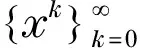





5 结 论
