基于能力约束的地震灾害应急救援调度优化研究

,,

(上海理工大学 管理学院,上海 200093)

地震作为人类面临的一种主要自然灾害,给人类的生命、财产安全带来了极大的威胁,对地震灾害等突发事件的应急救援调度研究尤为重要.应急救援调度优化是研究如何合理地安排灾后救援活动及配置医院能力,确保地震等灾害应急救援的有序进行以及救援目标的实现.

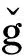
但是,这些关于突发应急的文献很少考虑将伤员运至医院后接受救治并随时间流动而造成医院容量动态变化的情况.本文将医院伤员因救治与运输的时间差而产生的流动性考虑到应急救援调度模型中,实时计算医院的实际可救治伤员数,从而提高医院的利用率,尽可能地降低伤员等待救治的时间.地震发生后形成单一灾害点,但受灾区域伴随时间变化逐步发展为多个灾害点,所以,本文分别从单灾害点多医院和多灾害点多医院两个方面建立伤员应急救援调度模型,并通过算例验证模型算法的可行性.并且,在受灾区域,能提供运输伤员的总车辆数是有限制的,且由于伤员的受伤状态和灾区各道路所遭到的不同程度的破坏,不同受灾点到不同医院的运输能力也受到限制,因此,要最大化地提高车辆的利用率,尽早地将所有伤员运至医院进行救治,就要尽可能地减少车辆的等待时间,让救援车辆一直处于往返在各受灾点和各医院的行驶状态,所以,在车辆完成一次调度时,立即根据不同灾害点到不同医院的运输时间及医院容量进行调度.

1 单灾害点多医院应急救援调度优化

单灾害点多医院的应急救援模型在实际的应用中相对较少,但在地震初发到之后的某段时间内,灾害点单一,该段时间内开展单灾害点多医院的救援.与此同时,单灾害点救援模型不论是在实际救援中还是在模型构建中都是多灾害点救援模型的基础,因此,单灾害点救援模型有利于全面阐述地震发生时的救援策略,且能对多灾害点救援模型进行有效过渡.

单灾害点多医院的救援模型将伤员以最短的时间运至医院进行救治作为第一优先级的约束.灾害点A处的运输能力受限,每次只能选择运往一所医院,返回灾害点后再根据各医院的救治能力和到各医院的运输时间选择运往另一所医院.在本文的研究中,不考虑伤员从灾害点到医院的运输成本,并假定在每一次的伤员调度中,都能有满足容量要求的医院对伤员进行救治.

1.1 调度优化模型构建

现对单灾害点模型符号进行说明.

A:地震灾害点;

X:灾害点A的伤员总数;

G:灾害点的单次运输能力;

Bj:编号为j的医院,j=1,2,…,n;

Yj: 编号为j医院能够同时作业最大容量,j=1,2,…,n;

Wj: 编号为j的医院的实际可用容量,j=1,2,…,n;

vj:编号为j的医院的伤员流动速度,j=1,2,…,n;

tj: 灾害点A到救治点Bj的单程运输时间,j=1,2,…,n;

tkj:应急点A第k次调运的单程时间,运往的医院是Bj,j=1,2,…,n;

N:灾害点A需要调运的次数;

rkj:灾害点A第k次调运的实际调运人数,运往的医院是Bj,j=1,2,…,n.

Φ:伤员全部运至医院所采取的方案.

Z:整数集.

假设:至少存在1个Bj使得rkj≤Wj,意为A在进行第k次调运时一定会有满足容量的Bj供A调运.

(1)

(2)

G=min {X,G}

(3)

rkj≤Wj,j=1,2,…,n

(4)

rkj≤G

(5)

1.2 优化模型求解

现介绍模型求解步骤.

步骤1在所有的tj(j=1,2,…,n)中选择最小的te,若G≤We(此时We=Ye),则选择Be对A进行调度.若te=te′,则对max(rke,rke′)所对应的Be对A进行调度.若G>We(此时We=Ye),则忽略掉该te,选择次小的te,重复该步骤,直到在剩余的tj中选出满足G≤We的te,选择Be完成对A的调度.赋值k=k+1.te表示灾害点A到救治点Be单程运输时间.e,e′∈{j|j=1,2,…,n}.te′表示灾害点A到救治点Be′单程运输时间;rke′表示应急点A到救治点Be′的单程运输时间.

步骤2若k>N,则停止调度;否则,步骤继续进行.车辆返回灾害点时,各医院的容量为W1=Y1,W2=Y2,…,We=Ye-r1e+vet1e,We+1=Ye+1,…,Wn=Yn,用步骤1的方法再度对A进行调度,假设选择Bf完成对A的调度.赋值k=k+1.

步骤3若k>N,则停止调度;否则,步骤1继续进行.车辆返回灾害点时,各医院的容量为

步骤4用步骤1的方法完成第k次调度,转入步骤3.

2 多灾害点多医院应急救援调度优化

地震发生后灾区随着时间的变化,单灾害点逐渐演化成多灾害点,因此,在地震发生后的伤员调度中所用到的模型绝大多数是多灾害点多医院的调度模型,该模型的构建虽然较为复杂但具有很强的实际意义.并且在以往的文献中很少有对地震发生时伤员运输的研究,关于地震灾害的研究多集中在救援物资的运输上,多灾害点多医院的救援调度模型在一定程度上填补了当前文献的空白,对地震灾害伤员的调度起着一定的理论指导意义.

多灾害点多医院的救援同样以最短的伤员运输时间作为第一优先级的约束,较单灾害点而言,多灾害点救援问题较为复杂.图1 (见下页)是一个多灾害点多医院伤员调运示意图,图中有4个灾害点和3所医院,在开始时(0时刻) 4个灾害点根据医院容量要求及从灾害点到医院的运输时间进行第一次的救援调度,车辆最早返回的灾害点立即进行下一次的救援调度,模型直至所有的灾害点的伤员全部运至医院方能结束.在本文的研究中,不考虑伤员从灾害点到医院的运输成本,并假设在每一次的伤员调度中,都能有满足容量要求的医院对伤员就行救治.

图1 多灾害点多医院调度模型图Fig.1 Model of multiple disaster points multiple hospitals

2.1 调度模型构建

现对单灾害点模型符号进行说明.

Ai:标号为i的地震灾害点,i=1,2,…,m;

Xi:各个应急点需要救治人数,i=1,2,…,m;

Gi:突发点Ai处的运输能力,i=1,2,…,m;

Bj:标号为j的医院,j=1,2,…,n;

Yj:医院能够同时作业的最大容量,j=1,2,…,n;

Wj:医院Bj的实际可用容量,j=1,2,…,n;

vj:医院Bj的伤员流动速度,j=1,2,…,n;

Ni:第i个灾害点需调运的次数,i=1,2,…,m;

tij:灾害点Ai到医院Bj的单程运输时间;i=1,2,…,m

tikj:灾害点Ai第k次往医院Bj调运的单程时间;i=1,2,…,m

rikj:Ai第k次往Bj调运的人数,j=1,2,…,n;

Tik:灾害点Ai第k次调运完返回后的最早时刻(ik≤Ni),当ik=Ni时,Ai不再参与调度.

Φi:灾害点i的伤员全部运至医院所采取的方案.

假设:至少存在1个Bj使得rik≤Wj,意为Ai在进行第k次调运时一定会有满足容量的Bj供Ai调运.

(6)

minT=max minT(Φi)

(7)

(8)

Gi=min {Gi,Xi}Gi>0

(9)

rikj≤Wj,i=1,2,…,m,j=1,2,…,n

(10)

rikj≤Gi

(11)

2.2 优化模型求解

现介绍模型求解步骤.

步骤2重新计算各救治点B1,B2,…,Bn,容量分别为Y1,Y2,…,Yf-Ge,Yn,不再考虑步骤1已完成调度的Ae,对剩余的地震灾害点Ai(i=1,2,…,m,i≠e)用步骤1的方法完成第一轮的调运.运输后各救治点容量

步骤3第一轮调运完后各车辆均返回灾害点时的时刻为Ti1,从Ti1中选出最小值Th1,到Th1时,各救治点的救治时间

此时,各救治点B1,B2,…,Bn容量为

对Th1所对应的Ah用步骤1的方法进行调度.

步骤4调运后计算并重置该时刻各救治点容量

此时仅有上轮发生调度的灾害点的容量发生了变化,即未产生调度的灾害点不进行此式的计算,得到新的一组Tik,进入步骤5.

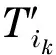
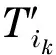
3 算例分析

3.1 单灾害点多医院算例

当某一地区发生地震灾害时,在地震发生初时,受灾地区较为集中,可视为单灾害点多医院救援问题.救援中医院容量、伤员流动率、灾害点到各医院的时间、灾害点的伤员总数、运输能力如表1所示.

3.2 多灾害点多医院算例

地震发生一段时间后,原本受到严重损坏的建筑、道路等设施因余震等因素而塌方,单灾害点随着时间的推移逐步发展为多灾害点.假设某地区在地震发生后有4个灾害点需要救援,有3所医院参与应急救援.救援中医院容量Yj,伤员流动率vj,灾害点到各医院的时间tij,灾害点的伤员总数Xi及运输能力Gi如表3所示.

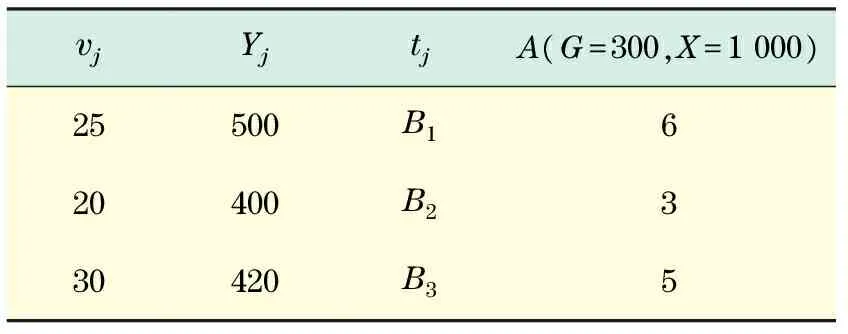
表1 1个地震灾害点3个医院初始数据Tab.1 Initial data of one earthquake disaster point and three hospitals

对表3的数据进行仿真分析,突发事件灾害点A1,A2,A3,A4所需运输伤员次数分别为N1=5,N2=4,N3=3,N4=3,根据模型的求解方法,得出该仿真案例求解结果如表4所示(见下页).

3.3 结果分析

以较为复杂的多灾害点多医院算例为例,计算出不考虑医院内伤员流动情况的救援时间,表5(见下页)的数据中不仅有B1,B2,B3这3所医院,另外,还假设了B4,B5,B6这3所医院参与应急救援才能完成救援任务.

表2 1个地震灾害点3个医院的算例求解Tab.2 Solution of the example of one earthquake disaster point and three hospitals

表34个地震灾害点3个医院的初始数据
Tab.3Initialdataoffourearthquakedisasterpointsandthreehospitals

XiGiAitijB1(Y1=500，v1=400)B2(Y2=400，v2=300)B3(Y3=1000，v3=50)X1=1000G1=200A1435X2=450G2=120A2869X3=800G3=300A3568X4=1200G4=400A4644

表4 4个地震灾害点3个医院的算例求解Tab.4 Solution of the example of four earthquake disaster points and three hospitals

在不考虑伤员流动的调度模型中,同样进行了15次调运,前10次调运,m=4,即4个灾害点都在参与调度.在T42=16时,进行对A4的第3次调运,此后A4不再参与调运,第11,12次调度时,m=3,在T32=24时进行对A3的第3次调运,此后A3不再参与调运,第13,14次调运,m=2,在T14=42时进行对A1的第5次调运,此后A1不再参与调运,第15次调运时,m=1,即只有1个灾害点参与调运,在T23=44时进行对A2的第4次调运,此后所有伤员运送至医院,整个调度系统结束调运,整个调度过程的总用时为minT=T23+t245=44+10=54.因为,不考虑伤员流动,在第4次调运后,医院B2的剩余可用容量W2=80,不再满足参与救援调度的条件.在第5次调运后,医院B1的剩余可用容量W1=0,不再满足参与救援调度的条件.在第9次调运后,医院B3的剩余可用容量W3=0,不再满足参与救援调度的条件.在第10次调运后,医院B5的剩余可用容量W5=100,不再满足参与救援调度的条件.在第13次调运后,医院B4的剩余可用容量W4=60,不再满足参与救援调度的条件.

表5 不考虑医院伤员流动的初始数据Tab.5 Initial data of hospitals ignoring wounded’s flow

图2是将考虑和不考虑伤员流动的两种不同计算过程进行汇总的一张对比图,横轴n表示第n次调运,两种算法都需要15次调运,纵轴T对应每次调运后伤员到达医院的时间,其计算方式为T=Tik+tikj.图2中的信息显示,在前6次调运中,两种方法所达到的效果相同,但是,随着调运的继续进行,由于不考虑伤员流动情况下的医院的容量达到上限后不能继续参与调度,模型中必须加入新的相对更远的医院参与救援,导致调运时间变长,即救援效果变差.

在仿真案例中,共4个地震灾害点3 450个伤员在有道路运输能力约束和医院救治容量约束的情况下用时42个时间单位被全部运输至医院进行抢救,参与救治的有3所医院.在不考虑医院内伤员流动的情况下,所有医院的容量总和必定大于3 450,所以,另有3个更远的医院参与到应急救援中,此时所有医院的容量之和为4 200,相对于考虑伤员流动的模型来说,浪费了大量的医院资源,更为严重的是拖延了救治时间,所有伤员要经过54个时间单位才能全部运至医院进行救治,比考虑医院内伤员流动的模型要延误12个时间单位.

图2 两种算法计算过程汇总图Fig.2 Summary of the two calculations

4 结 论

研究了地震发生后伤员运输至医院进行救治的问题,分单灾害点多医院和多灾害点多医院进行建模和仿真.在模型的构建中考虑了道路的运输能力约束和医院容量约束,模型中集合了伤员流动的思想,使研究更符合实际情况,并在算例的验证中将未考虑伤员流动情况的计算结果与考虑伤员流动情况的计算结果进行对比,体现伤员流动在模型建立中的重要性.这对突发事件应急调度的动态分析具有重要意义.在进一步的研究中,还需要针对模型的特点开发具有更高计算性能的求解算法,来解决更加复杂的伤员运输模型.

[1] LARSON R C,METZGER M D,CAHN M F.Responding to emergencies:lessons learned and the need for analysis[J].Interfaces,2006,36(6):486-501.

[2] SIMPSON N C,HANCOCK P G.Fifty years of operational research and emergency response[J] Journal of the Operational Research Society,2009,60(S1):S126-S139.

[3] 姜艳萍,樊治平,苏明明.应急决策方案的动态调整方法研究[J].中国管理科学,2011,19(5):104-108.

[4] ÖZDAMAR L,EKINCI E,KÜÇÜKYAZICI B.Emergency logistics planning in natural disasters[J].Annals of Operations Research,2004,129(1/4):217-245.

[5] HAGHANI A,OH S C.Formulation and solution of a multi-commodity,multi-modal network flow model for disaster relief operations[J].Transportation Research Part A:Policy and Practice,1996,30(3):231-250.

[6] FIEDRICH F,GEHBAUER F,RICKERS U.Optimized resource allocation for emergency response after earthquake disasters[J].Safety Science,2000,35(1/3):41-57.

[7] JAE Y.Stochastic scheduling problems for minimizing tardy jobs with application to emergency vehicle dispatching on unreliable road networks[D].New York:University of New York,2003.

[9] JAGTENBERG C J,VAN DEN BERG P L,VAN DER MEI R D.Benchmarking online dispatch algorithms for Emergency Medical Services[J].European Journal of Operational Research,2017,258(2):715-725.

[10] WILMER I,CHALK G,DAVIES G E,et al.Air ambulance tasking:mechanism of injury,telephone interrogation or ambulance crew assessment?[J].Emergency Medicine Journal,2015,32(10):813-816.

[11] CLARK A,CULKIN B.A network transshipment model for planning humanitarian relief operations after a natural disaster[M]//VITORIANO B,MONTERO J,RUAN D.Decision Aid Models for Disaster Management and Emergencies.Paris:Atlantis Press,2013.

[12] KNIGHT V A,HARPER P R,SMITH L.Ambulance allocation for maximal survival with heterogeneous outcome measures[J].Omega,2012,40(6):918-926.

[13] 刘春林,何建敏,盛昭瀚.多出救点应急系统最优方案的选取[J].管理工程学报,2000,14(1):13-15.

[14] 潘郁,余佳,达庆利.基于粒子群算法的连续性消耗应急资源调度[J].系统工程学报,2007,22(5):556-560.

[15] 杨继君,许维胜,黄武军,等.基于多灾点非合作博弈的资源调度建模与仿真[J].计算机应用,2008,28(6):1620-1623.

[16] 曹庆奎,刘新雨,任向阳.基于模拟植物生长算法的车辆调度问题[J].系统工程理论与实践,2015,35(6):1449-1456.

[17] 代颖,马祖军,郑斌.突发公共事件应急系统中的模糊多目标定位-路径问题研究[J].管理评论,2010,22(1):121-128.

[18] 张国富,王永奇,苏兆品,等.应急救援物资多目标分配与调度问题建模与求解[J].控制与决策,2017,32(1):86-92.