基于t函数的稳健变量选择方法

,,

(上海理工大学 理学院,上海 200093)

随着数据获取技术的迅猛发展,人们获取的数据结构越来越复杂,维数越来越高.统计学的主要任务就是对观测数据的因变量和自变量建立模型,进而对数据进行分析、预测以及一些统计推断.在现实问题中,因变量往往同时受多个自变量影响,但这些影响并不都很显著.人们通常希望在模型中只引进对因变量有重要影响的自变量,所以,变量选择就成了建模前的必要工作.但是,现实问题中,数据经常被污染,往往存在异常值,这时用普通的变量选择方法就会对模拟结果产生很大的偏差.

针对变量选择的问题,统计学家已经作出了大量研究.1996年,统计学家Tibshirani[1]提出了一种变量选择方法LASSO,基本思想是在最小二乘法的基础上施加L1惩罚.2001年,Fan等[2]提出了变量选择的SCAD方法,并研究了该方法的Oracle性质.在某些LASSO不相合的情况下,Zou[3]又提出Adaptive LASSO,该方法是对LASSO的一种改进,能够满足Oracle性质.为了克服LASSO的一些缺点,Zou等[4]提出了Elastic Net变量选择方法.针对高维数据,Candès等[5]提出了Dantzig Selector方法.

针对数据中可能存在异常值这一情况,有许多文献已经研究了稳健估计与稳健变量选择方法.文献[6-7]率先提出当正态分布被污染时,估计位置参数的渐进理论.文献[8-9]将最小一乘法用到稳健估计中,之后文献[10]进一步分析最小一乘法的优良性质.文献[11]提出了基于t函数的稳健估计方法,考察了基于t函数估计量的优良性.同时研究稳健估计方法的还有文献[12-14].文献[15]提出了基于Huber函数的针对纵向数据的稳健变量选择方法.针对稳健估计中常用的t函数和Huber函数,文献[16]提出了基于M估计的稳健向前变量选择方法,并进一步考察了t函数和Huber函数在稳健向前变量选择中的性质.

本文在前人研究的基础上,提出一种新的基于t函数的稳健变量选择方法,并与文献[15]中基于Huber函数的稳健变量选择方法进行比较.模拟结果显示,t函数方法对数据中的异常值有更好的限制作用,可以达到更好的变量选择效果.文章主要分为5个部分,第1部分介绍了稳健的惩罚估计方程.第2部分将t函数和Huber函数的性质进行比较分析,突出t函数在稳健变量选择方法中的优势.第3部分介绍本文中所用的算法.第4部分是数值模拟,通过3种污染方式来污染数据,比较本文方法与文献[15]中方法的模拟效果.第5部分为结论.

1 稳健的惩罚估计方程

考虑如下线性模型:

y=xβ+ε

(1)

式中:y=(y1,y2,…,yn)T;x=(x1,x2…,xn)T,xi=(xi1,xi2,…,xip);β=(β1,β2,…,βp)T;ε=(ε1,ε2,…,εn)T,且i=1,2,…,n,εi的期望值为0,方差为σ2,ε的各分量相互独立.

与文献[12]类似,考虑如下稳健估计方程

(2)

式中,Wi是权重矩阵W的第i个分量,权重Wi通过文献[13]得来,用来降低自变量中异常值的影响,定义如下:

(3)

式中:r为大于1的常数;p0为自由度与xi维数相同的卡方分布的0.95分位数;取mx为xi的中位数,则mx的第k个分量取为x第k列的中位数;Sx的第k个对角元取为1.483(median|x(k)-mx(k)⊗In|),x(k)表示x的第k列,mx(k)表示mx的第k个分量,⊗表示kronecker乘积,In表示n维元素全为1的列向量.

式(2)中,函数φ(·)是一个有界得分函数,用来限制因变量中异常值的影响,本文将此函数定义为自由度为2的t函数,记作t2函数.当φ(x)=x且Wi=1时,原稳健估计方程就退化成一般的估计方程,不再具有稳健性,即为非稳健的估计方程,此时估计方程(2)会对异常值有较大的敏感性.

通过求解式(2),可以得到稳健参数估计.为了同时达到变量选择的效果,采用压缩估计方法,即在估计方程中再添加一个惩罚项.因此考虑惩罚稳健估计方程

nqλ(|β|)sgn(β)=0

(4)

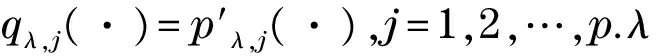
本文所考虑的惩罚函数主要是SCAD惩罚函数[3].取惩罚函数为

2 t函数与Huber函数

t分布的密度函数为

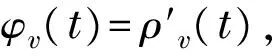
Huber分布的密度函数为

其中

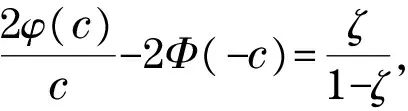
自由度不同,t分布密度函数的尾部厚度不同,从而t函数对异常值的抑制效果不同.图1是自由度分别为2,6,10的t分布密度函数,由图1可见,自由度越小,密度函数的尾部越厚.文献[16]已经证明厚尾性对异常值有更好的抑制作用.图2是自由度为2的t分布密度函数和Huber分布密度函数的图像比较,由图2显然可见,t分布密度函数的尾部更厚.由此可以初步推断,基于自由度为2的t函数的稳健压缩估计可以对异常值有更好的限制作用.下面,进一步分析t函数和Huber函数的图像区别,以及通过图像显现出来的对异常值的作用效果,如图3和图4所示.

图1 不同自由度的t分布密度函数Fig.1 t distribution density function with different kinds of degree of freedom

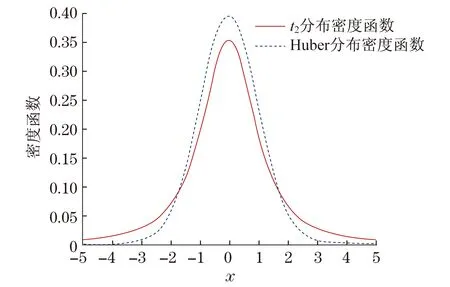
图2 t分布和Huber分布密度函数比较Fig.2 Comparison density function between t distribution and Huber distribution

图3 t函数Fig.3 t function

图4 Huber函数Fig.4 Huber function

图3是自由度分别为2,6,10的t函数的图像,由图3可见,t函数并不是单调的,而是一个回降函数,而且随着自由度的增大,在一定自变量范围内,函数的变化范围在变小.可以看出,当变量t的绝对值变大时,t函数将会对这些绝对值较大的变量产生作用,使其函数值接近于0,因此t函数可以很好地抑制数值模拟中异常值的影响.尽管自由度不同的t函数对较大异常值的抑制作用不相上下,但图3表明,当变量t处在正常值范围内时,自由度越大的t函数会对变量施加越大的抑制作用,使原本正常的数据也受到更大的影响,从而破坏了数据原有的真实性.所以,综合而言,t2函数是最优的.本文将选取自由度v=2.

文献[11]也模拟分析了自由度分别为1和4的t函数在M估计中的稳健性,其模拟结果表明,自由度为1的t函数比自由度为4的t函数具有更好的稳健性.本文也模拟分析了自由度分别为1和2的t函数在变量选择中的稳健性.结果表明,自由度为1的t函数和自由度为2的t函数的模拟结果比较接近.在模拟设置下,自由度为2的t函数比自由度为1的t函数在变量选择和参数估计方面稍好一些,因此本文只报告自由度为2的t函数的结果.文献[16]也得出了与本文相类似的结论,它们的研究表明,在M估计中,取自由度较小的t函数对异常值有较好的限制作用.

通过图3和图4的比较可见,当自变量趋于正无穷时,Huber函数值为+2,当自变量趋于负无穷时,Huber函数值为-2.而无论自变量趋于正无穷还是负无穷,t2函数值始终趋近于0.因此,t2函数的稳健方法能减小异常值在模型估计中的作用,更好地削弱异常值的影响[14].所以,t2函数在变量选择中比Huber函数具有更好的稳健性.

3 算法

本文算法与文献[15]类似,采用牛顿迭代法,具体算法如下:

a.对给定的一个λ值,首先计算β的初始值β(0).本文取最小二乘估计作为初始值.

b.用β(k)表示第k次迭代所得的估计值,k≥0,则

β(k+1)=β(k)-[Dβ(k)-Δλ(β(k))]-1Rp(β(k))

这里,D为p阶导数阵∂(Rp(β))/∂β.

Δλ(β)=diag(qλ(|β1|)/(δ+|β1|),…,

qλ(|βp|)/(δ+|βp|))

式中,δ是一个非常小的正数,文中取值为10-4.

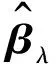
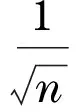
4 数值模拟

通过式(1)产生真实数据,这里令β=(3,2.5,0,0,3,0,0,0)T,xi取自p维多元正态分布,即xi～N(0,Ip),这里p=8.随机误差ε1,ε2,…,εn相互独立,且都服从标准正态分布.

为了全面考察本文所提方法的稳健性,这里将对数据进行2种污染力度、3种污染方式来产生异常值.通过2种污染力度在数据中分别产生较大异常值和较小异常值.污染方式1是随机选取5个样本只对x进行污染,将原本xi变为xi+5(或xi+2.5);污染方式2是随机选取5个样本只对y污染,将原本yi变为yi+10(或yi+3);污染方式3是随机选取3个样本对x污染,再随机选取2个样本对y污染,且所选样本不重复,将选取的xi变为xi+5(或xi+2.5),yi变为yi+10(或yi+3).

为了排除随机性对该方法的影响,本文将重复模拟200次,采用8个指标来衡量各种方法的效果.首先用估计的偏差、方差和均方误差来衡量估计的优劣;另一方面,用取对率、拟合不足率、拟合过度率、取对个数和取错个数来衡量变量选择的优劣.其中,取对率就是将β中原本为0的分量估计为0,且将β中原本非0的分量估计为非0的总次数在200次模拟中的比率.拟合过度率为将β中原本的非0估计为非0,原本为0的也估计为非0的总次数在200次中的比率.拟合不足率即为200次模拟中,估计结果将β中原本不为0的估计为0的总次数在200次中的比率.取对个数是200次模拟中正确估出0的个数的平均值,取错个数是200次模拟中将原本非0估计为0的个数的平均值,取对个数最好为5,取错个数最差为3.

SCAD方法是变量选择中比较常见的惩罚方法,由文献[2]可知,SCAD方法在稳健变量选择中具有较好的优良性,因此本文主要模拟不同SCAD方法的稳健效果.表1～3分别表示污染1,2,3情况下各种方法变量选择的模拟结果,表中字体倾斜的数据表示污染力度较小的结果.SCAD-NR表示方程(4)中φ(x)=x且wi=1时的非稳健方法;SCAD-R (Huber)表示文献[15]中所提的基于Huber函数的SCAD稳健方法;SCAD-R (t2)表示本文所提的基于t2函数的SCAD稳健方法.通过与非稳健方法的比较,凸显出本文所提方法与文献[15]中方法是稳健的.在数据中存在异常值时,稳健估计结果明显好于非稳健的.而通过本文方法与文献[15]中方法比较,模拟结果证明本文所提的方法在变量选择上的效果明显优于基于Huber函数的方法.

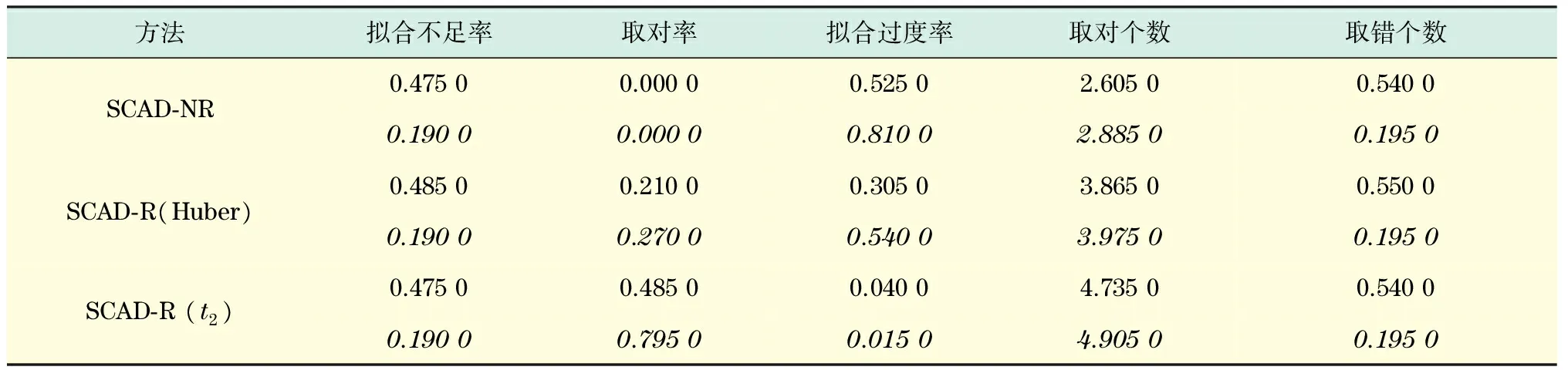
表1 污染1情况下变量选择的模拟结果Tab.1 Simulation results of variable selection under pollution 1

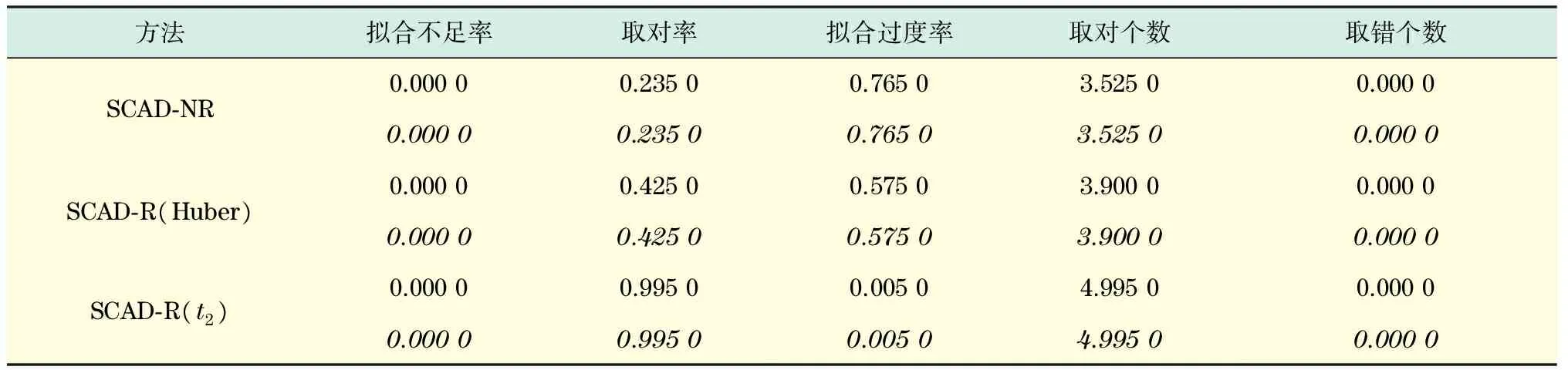
表2 污染2情况下变量选择的模拟结果Tab.2 Simulation results of variable selection under pollution 2

由表1～3可见,在不同污染力度和不同污染方式下,非稳健方法选择的效果总体来说都没有稳健方法好.非稳健方法拟合过度率比两种稳健的方法都高,也就是说,非稳健方法总会把β中原本为0的估计为非0.由表中模拟结果可见,基于t函数的稳健方法取对率总是最高的.无论是哪种污染方式,本文所提的方法与非稳健方法和文献[15]中的方法相比,取对率都远大于其他两种方法,而且取对个数也明显大于其他两种方法.虽然在拟合不足率上看不出本文所提方法的优势,但是,这里几种方法的拟合不足率都非常接近,而在正确率、拟合过度率和取对率方面,却明显可以看出本文所提方法的优势.可见,本文方法对异常值的抵抗力比文献[15]中基于Huber函数的稳健方法更强,大大减少异常值在模型估计中引起的偏差.

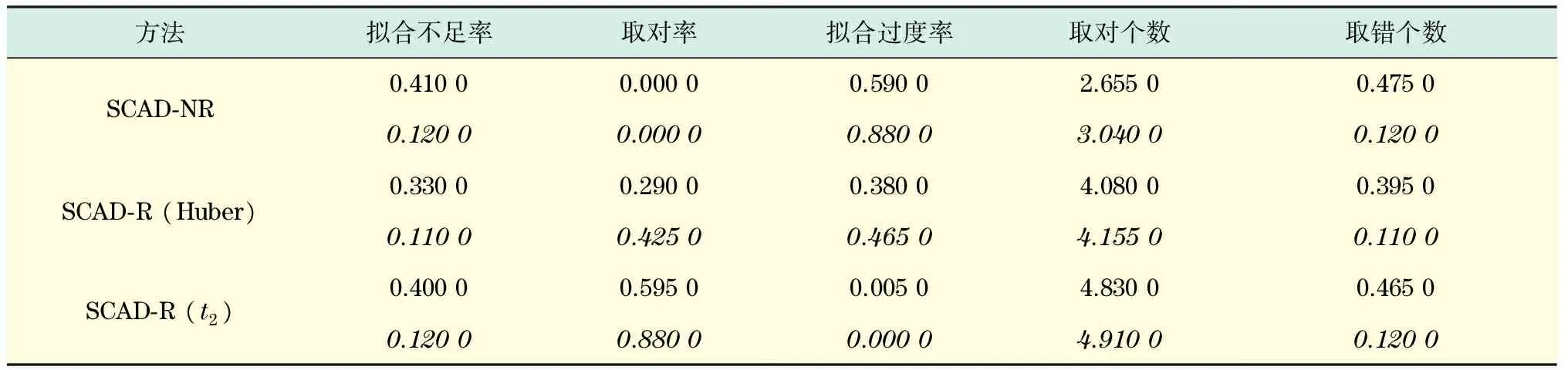
表3 污染3情况下变量选择的模拟结果Tab.3 Simulation results of variable selection under pollution 3

表4是在2种污染力度下第1种污染方式对β中非0分量的估计结果,统计了各非0分量的偏差、方差和均方误差.从该结果中可见,两种稳健方法在估计方面也明显优于非稳健方法,本文方法此时较文献[15]并没有很明显的优势.在偏差的第1个分量和方差的第2,3个分量甚至稍微变大,但均方误差却稍有优势.相比较来说,基于t2函数的均方误差比Huber函数的稍小.

表4 污染1情况下估计的模拟结果Tab.4 Simulation results of estimation under pollution 1

综合表1～4,在非零参数估计上本文方法与文献[15]中方法相比具有较小的均方误差,同时本文方法在变量选择方面的稳健性和优势较为突出,其对异常值的抵抗力比文献[15]中方法更强.

5 结 论

本文在前人研究的基础上提出基于t2函数的稳健变量选择方法,并与文献[15]中稳健方法进行比较,通过数值模拟来验证本文方法的有效稳健性.文中首先详细叙述了关于该方法的模型理论,在稳健估计方程中施加一个惩罚函数,来达到期望的稳健变量选择效果.然后在第2部分进一步考察稳健方程中的有界得分函数,通过比较不同自由度的t函数与Huber函数的性质,初步判断方程(4)中的有界得分函数的稳健性.第3部分介绍了本文所用的算法,采用牛顿迭代法.最后通过第4部分的数值模拟来验证前文中预计的稳健性.模拟结果体现了t2函数在变量选择方面的明显优势,虽然参数估计的结果并不是明显好于Huber函数的结果,但是通过取对率、拟合不足率、拟合过度率、取对个数和取错个数体现的选择结果,说明t2函数在变量选择上的稳健性优于Huber函数.

本文主要通过模拟来考察各种方法的优劣.基于t函数的变量选择方法的大样本性质,以及将该方法应用到更复杂的纵向数据中,或应用到超高维的横截面数据中,这些问题还有待进一步研究.

[1] TIBSHIRANI R.Regression shrinkage and selection via the lasso:a retrospective[J].Journal of the Royal Statistical Society,2011,73(3):273-282.

[2] FAN J Q,LI R Z.Variable selection via nonconcave penalized likelihood and its oracle properties[J].Journal of the American Statistical Association,2001,96(456):1348-1360.

[3] ZOU H.The adaptive lasso and its oracle properties[J].Journal of the American Statistical Association,2006,101(476):1418-1429.

[4] ZOU H,HASTIE H.Regularization and variable selection via the Elastic Net[J].Journal of the Royal Statistical Society,2005,67(2):301-320.

[6] HUBER P J.Robust estimation of a location parameter[J].The Annals of Mathematical Statistics,1964,35(1):73-101.

[7] HUBER P J.Robust regression:asymptotics,conjectures and Monte Carlo[J].The Annals of Statistics,1973,1(5):799-821.

[8] PORTNOY S,KOENKER R.The Gaussian hare and the Laplacian tortoise:computability of squared-error versus absolute-error estimators[J].Statistical Science,1997,12(4):279-300.

[9] GILONI A,PADBERG M.Alternative methods of linear regression[J].Mathematical and Computer Modelling,2002,35(3/4):361-374.

[10] GILONI A,PADBERG M.The finite sample breakdown point ofL1-regression[J].Journal on Optimization,2004,14(4):1028-1042.

[11] HE X M,SIMPSON D G,WANG G Y.Breakdown points of t-type regression estimators[J].Biometrika,2000,87(3):675-687.

[12] HE X M,FUNG W K,ZHU Z Y.Robust estimation in generalized partial linear models for clustered data[J].Journal of the American Statistical Association,2005,100(472):1176-1184.

[13] SINHA S K.Robust inference in generalized linear models for longitudinal data[J].The Canadian Journal of Statistics,2006,34(2):261-278.

[14] MARONNA R A,MARTIN R D,YOHAI V J.Robust statistics:theory and methods[M].Chichester,England:John Wiley and Sons,2006.

[15] 樊亚莉,徐群芳.稳健的变量选择方法及其应用[J].上海理工大学学报,2013,35(3):256-260.

[16] SCHUMANN D H.Robust variable selection[D].Carolina:North Carolina State University,2009.