复合式电磁作动器设计及特性试验

彭 虎 张进秋 刘义乐 彭志召 张 建 张立君

1.装甲兵工程学院技术保障工程系,北京,1000722.装甲兵工程学院装备试用与培训大队,北京,1000723.装甲兵工程学院教练团,北京,100072

0 引言

车辆悬挂系统起支撑车体并缓和来自路面不平度冲击的作用，传统被动悬挂将路面激励引起的振动能量以热量的形式耗散，不仅浪费能源，且使阻尼器工作在较高温度下，缩短了阻尼器使用寿命[1-2]。若能采用一定的能量回收装置将该部分能量加以回收再利用，不仅可以提高车载用电设备的续航能力，起到节能的作用，还可以降低阻尼器温度，提高其可靠性，延长其使用寿命[3]。

电磁悬挂是一种可将悬挂振动机械能转换成电能并加以回收的可控悬挂，电磁响应速度快，可提高能量转换速率，成为研究的热点[4-5]。电磁作动器作为一种可控悬挂装置，可在发电机和电动机两种工况下进行切换，实现主动振动控制和能量回收，但当前大多数电磁悬挂只能单独地进行振动控制或单独进行能量回收，两者之间的矛盾依旧难以解决[6-7]。由于单独的电磁悬挂存在电磁阻尼不足现象，不能满足车辆“失效-安全”特性要求，而磁流变减振器(magneto-rheological damper, MRD)作为一种阻尼可调的半主动可控装置，具有响应迅速、输出阻尼力大的特点，且当控制失效时，MRD基础阻尼仍可充当被动悬挂对悬挂系统起到保护作用[8-9]。

针对电磁悬挂及MRD各自的优缺点，本文以某型军用轮式越野车辆为对象，设计了一种旋转电机与MRD并联的复合式电磁作动器，试制了原理样机，并分别对其力学特性及馈能特性进行了台架试验。

1 复合式电磁悬挂系统结构

复合式电磁悬挂系统主要包括复合式电磁作动器、车辆状态传感器、控制系统、电源及能量存储装置、电机驱动器以及对MRD供电的程序控制电流源，复合式电磁悬挂系统结构如图1所示。

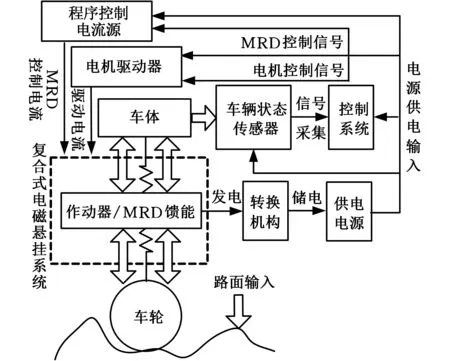
图1 复合式电磁悬挂系统结构图Fig.1 The structure diagram of composite electro-magnetic suspension system

该复合式电磁悬挂系统可工作于如下4种不同工况：

(1)被动馈能工况。不给MRD供电，只保留其基础阻尼，电机工作于发电机工况用于馈能，主要用于路面状况较好且无需振动控制的工况。

(2)主动控制工况。不给MRD供电，电机工作于电动机工况输出扭矩，通过运动转换机构变成悬挂间主动作动力进行主动控制，主要用于路面条件较差但对乘坐舒适性要求较高的场合，但控制持续时间不宜过长。

(3)半主动无馈能工况。将馈能电路断开，无电磁阻尼馈能，则悬挂系统仅由MRD工作，进行半主动控制，主要用于对振动控制要求不太高但又有必要进行控制的工况。

(4)半主动有馈能工况。电机作发电机用，电机的电磁阻尼进行馈能，MRD进行半主动控制，用于对振动控制和能量回收要求均不太高的场合，可实现振动控制和能量回收并存，解决两者之间存在的矛盾关系，这是该复合式电磁作动器的突出优点。

2 复合式电磁作动器结构设计

2.1 设计要求

以某型军用轮式越野平台(该车质量为1 250 kg)为基础，参照美军“枪骑兵”战车的主动悬挂系统设计要求[10]，结合该复合式电磁悬挂系统特点，提出如下设计要求：

(1)单个电磁作动器的额定出力为1/4车重的0.3倍即919 N，而最大出力为1/4车重的0.9倍即2 756 N。优化设计条件下，单独的电机+减速机出力在限定安装尺寸下难以满足如此大的出力要求。该复合式电磁作动器可通过控制MRD输出阻尼力，以补偿电机作动器部分主动出力的不足，但为了突出主动控制效果，电机主动控制力应大于出力要求的2/3，即额定出力为613 N，最大出力为1 838 N。

(2)为保证主动/半主动控制效果，由机械摩擦阻力与MRD基础阻尼力组成的基础阻力应越小越好，但过小又起不到“失效-安全”保护作用，综合考虑，基础阻力应不大于500 N。

(3)为保证半主动控制效果，同时补偿主动控制中所需的剩余1/3控制力(约306 N，最大918 N)，在悬挂相对运动速度0.52 m/s条件下，MRD部分应该提供至少1 000 N的可调阻尼力，相当于阻尼系数1 923 N·s/m。由于机械阻力难以控制，故MRD基础阻尼力应适当，介于150～300 N，可调倍数大于4.3。

(4)为提高馈能效率，电机应当具有较大的反电动势常数，Ke≥24V/(kr/min)。

(5)此外，悬挂系统需要至少100 mm的悬挂行程来满足减振及馈能的需求。

2.2 MRD设计

MRD部分主要由钢筒、活塞体、活塞杆及线圈组成，其中活塞体需要高磁导率、低磁滞性及较高的磁饱和度，以提高磁回路中的磁场强度和保证零磁场条件下的低阻尼力特性，因此，选用DT4电工纯铁作为活塞铁心材料；钢筒需要兼具一定的导磁性和较高的强度，选择45钢；活塞杆需要较高的强度，也选择45钢；线圈应具备较高的电磁转换效率和较高的性价比，选择铜质漆包线；为隔绝磁流变液(magneto-rheological fluid, MRF)与线圈，在线圈外侧用环氧树脂进行密封；单筒单出杆式MRD由于自身结构原因存在阻尼非对称现象，故采用浮动活塞式结构进行体积补偿。MRD活塞结构如图2所示。

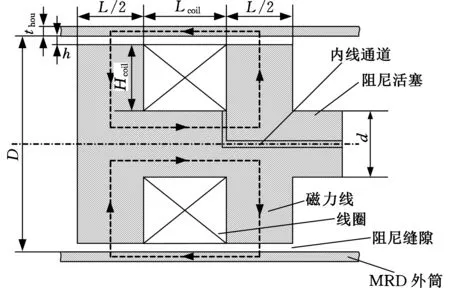
图2 MRD活塞结构图Fig.2 Structure diagram of MRD piston

MRD阻尼力表达式为

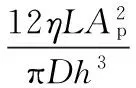
(1)

Ap=π(D2-d2)/4

式中，Fη为基础阻尼力；Fτ为库仑阻尼力；η为磁流变液零场黏度；L为有效阻尼缝隙长度；Ap为活塞有效面积；h为阻尼缝隙宽度；D为缸筒内径；d为活塞杆直径；τy为磁流变液剪切屈服强度；v为悬挂相对运动速度。

阻尼可调倍数ε表示阻尼力Fd与基础阻尼力Fη之比:

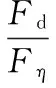
(2)

MRD工作时，活塞及钢筒相对运动产生高低压差，磁流变液在压差作用下通过阻尼缝隙在两腔之间流动，通过给线圈通电在缝隙处形成磁场，改变磁流变液的流动黏度，实现变阻尼。除结构设计外，另一个影响MRD性能的因素是磁流变液的性能，本文采用实验室自制的磁流变液，其表观黏度η=0.8 Pa·s，其剪切屈服应力与磁感应强度的关系如图3所示，磁流变液正常工作条件下磁感应强度一般在0.4～0.6 T，对应剪切屈服应力23 kPa左右，满足使用需求。拟合剪切屈服应力τy与磁感应强度B的关系可得

τy=-39B2+68B-1.3

(3)

由磁路欧姆定律推导可知，阻尼缝隙处磁感应强度

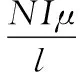
(4)

l=2Lcoil+Hcoil+L+0.5D+1.5h+thou

(5)

式中，I为控制电流；l为磁路平均长度；N为线圈匝数；μ为磁流变液磁导率，μ=7.54×10-6H/m；h为阻尼缝隙宽度；Lcoil为线圈长度；Hcoil为线圈宽度；thou为缸壁厚度。

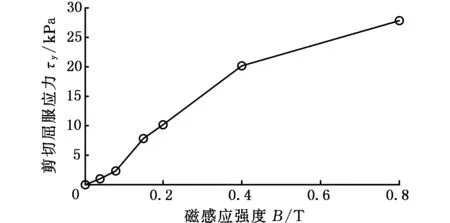
图3 磁流变液剪切屈服应力与磁感应强度的关系Fig.3 The relationship between the shear yield stress and magnetic induction intensity of MRF

线圈匝数可用下式估算：

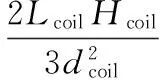
(6)

式中，dcoil为导线直径，本文取dcoil=0.5 mm,最大电流2 A。

MRD设计流程如图4所示，首先确定MRD所需最大输出阻尼力及可调倍数，以阻尼缝隙宽度及有效阻尼通道长度、活塞直径大小、线圈匝数等条件作为约束，利用磁流变液自身的剪切力与剪切屈服强度之间的关系，以及多目标遗传算法(multi-objective genetic algorithm, MOGA)进行参数优化，得到MRD设计参数最优解。若不能满足设计要求，则重新匹配计算，直到输出阻尼力和可调倍数均满足设计要求。

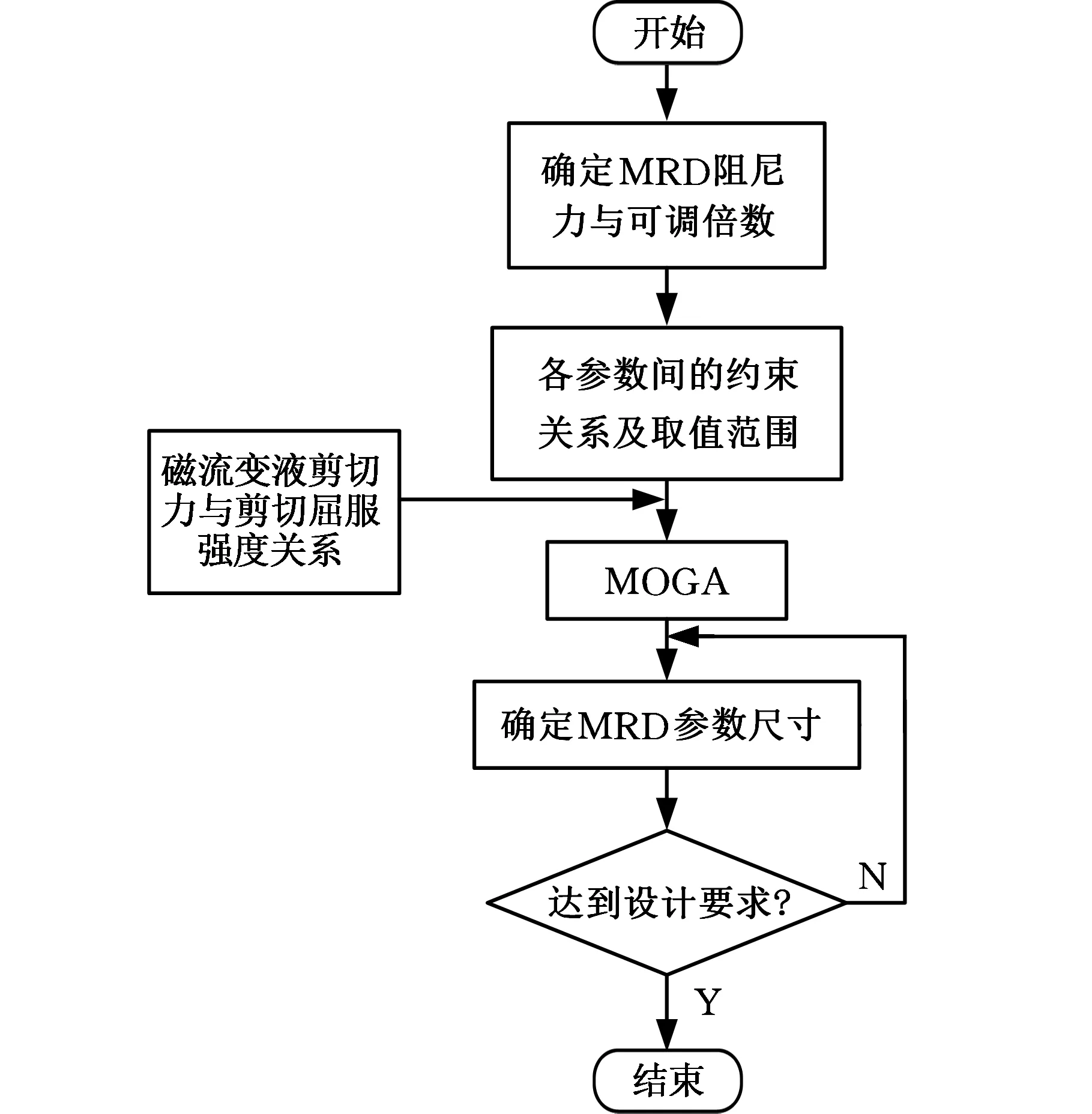
图4 MRD设计流程Fig.4 The design process of MRD

根据设计要求，需要MRD满足库仑阻尼力大于1 000 N，可调倍数大于4.3的条件，因此，以最大输出阻尼力Fdmax和可调倍数ε作为优化目标，7个约束参量为阻尼缝隙宽度h、有效缝隙长度L、阻尼活塞外径D、线圈尺寸Lcoil×Hcoil、缸壁厚度thou、活塞杆直径d。设计参量及取值范围如表1所示。

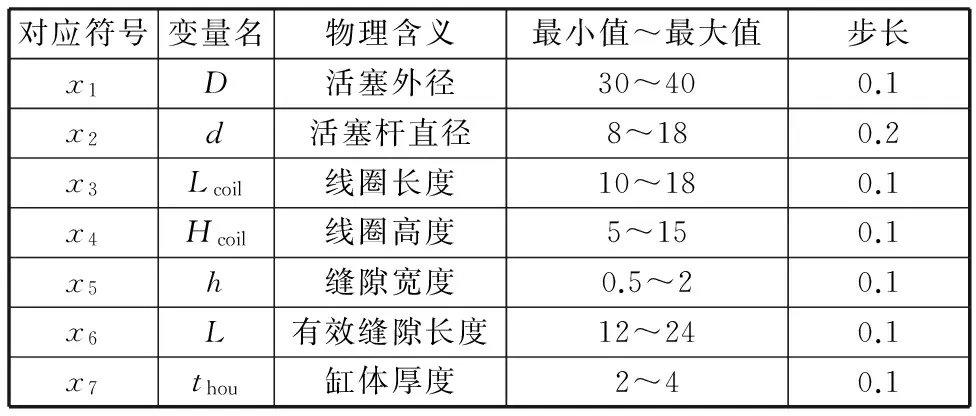
表1 设计参量及取值范围Tab.1 The design parameters and relative value range mm

目标函数为

(7)

约束条件为

(8)

初始种群为10，迭代次数为100，交叉概率为0.5，选择概率为0.05，突变概率0.1，采用MOGA对MRD设计参数进行寻优求解，经过3 000次迭代，可获得2 697组Pareto解集，如图5所示，图中深色的点为可行解，浅色的点为非可行解。

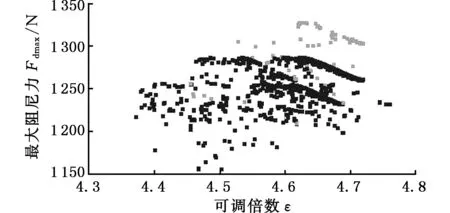
图5 Pareto解集Fig.5 The Pareto solution set

选取Pareto前沿一组优化后的设计参数作为最优解，最大阻尼力1 285 N，可调倍数4.64，基础阻尼力276.94 N，最大可调阻尼力1 008.1 N，满足设计要求，优化后的设计参数如表2所示。

表2 优化后的设计参数Tab.2 The optimized design parameters

对优化后的MRD模型进行磁场分析。MRD线圈产生的磁力线如图2所示，磁路由活塞铁心经过阻尼缝隙、钢筒、阻尼缝隙，而后回到活塞铁心处，形成闭环回路，通过改变加载电流的大小可改变磁场密度。利用Ansoft中的Maxwell 2D磁场分析软件对MRD进行磁场分析，验证磁路设计是否合理。线圈绕线直径0.5 mm，线圈匝数440，加载电流2 A，磁感应强度分布如图6所示。

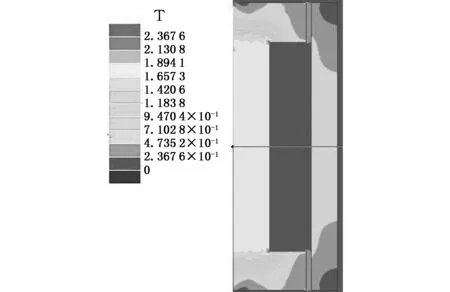
图6 MRD磁感应强度分布Fig.6 The magnetic induction intensity distribution of MRD

由图6可知，磁感应强度在磁回路中各个部分的分布并不相同，由于磁流变液磁导率比活塞体铁心及钢筒的磁导率小，故磁降产生主要在阻尼缝隙处。磁感应强度近似梯形分布，在铁心内部磁感应强度最大，约1.66～1.89 T，钢筒处次之，阻尼缝隙处最小，为0.44～0.58 T，平均有效磁场强度为0.51 T，磁流变液没有达到0.8 T的磁饱和状态，符合要求。

2.3 电机计算及选型

不计传递效率，电机与悬挂系统之间的运动转换公式可表示为

(9)

式中，Fan为齿条往复运动输出力，N；T为齿轮扭矩，N·m；n为电机转速，r/min；i为减速机构传动比；Rg为齿轮分度圆半径，m。

电机作发电机馈能时产生的感应电压

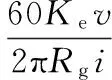
(10)

由电机输出扭矩传递到齿条上的主动出力

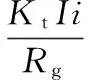
(11)

式中，Kt为电机转矩常数，N·m/A。

电机功率计算式为

P=Fanv

(12)

按照需要额定出力613 N计算，悬挂相对运动速度0.52 m/s时，由式(12)计算可得需要电机功率为319 W。若电机功率选择过小，会造成“小马拉大车”的现象，造成电机长期过载，使之绝缘部分因发热而烧坏，甚至造成电机的损毁；而电机功率选择过大，又会出现“大马拉小车”的现象，使其输出功率不能得到充分利用，功率因数和效率不高，造成能源浪费，同时增加了电机的重量。由此，根据机械传动效率和摩擦力等因素的影响，选择功率为600 W的电机。

旋转式永磁无刷直流电机具有体积小、响应快、作用力与体积比大等优点。调研选型MOTEC的HLM-9607H06LN型直流无刷电机作为该复合式电磁作动器的电机部分，电机额定电流7 A，额定扭矩2 N·m，额定转速3 000 r/min，最大转速5 000 r/min，反电动势常数30.4V/(kr/min)，转矩常数0.475N·m/A，96 V直流供电，功率600 W。

2.4 减速机计算及选型

减速机用以传递电机和悬挂系统间的转速和扭矩。根据设计要求，初选齿数19、模数3的齿轮，分度圆半径Rg=0.028 5 m，齿条采用圆形齿条，与常见的方形齿条相比，圆形齿条摩擦力更小，齿条齿形结构与齿轮一致。电机作主动控制出力时，若作动器峰值出力为1 838 N，则需要电机提供的扭矩约为52.38 N·m，电机额定转矩常数2 N·m，最大转矩常数6 N·m，由式(9)和式(11)计算可得所需传动比i不小于9；而作发电机进行能量回收时，当复合式电磁作动器相对运动速度达到0.52 m/s时，无减速机状态下，电机转速为174 r/min，电机反电动势常数为30.4V/(kr/min)，计算得反馈电压5.29 V。研究显示，当电机处于发电机低速运转状态时，与额定转速状态下的高速运转状态相比，其馈能发电效率非常低，所以从减振增扭和馈能增速的角度考虑，需要在电机和齿轮之间添加一个减速机，以提高减振及馈能性能。

当行星减速机的减速比为16时，不计效率，计算得齿条峰值出力4 036.3 N，额定出力1 122.8 N，电机转速2 787.7 r/min，低于额定转速3 000 r/min，由式(10)可得最大反馈电压84.64 V，具备良好出力及馈能特性。

为了与电机匹配，选择MOTEC-APE60-16行星减速机。设计加工原理样机，复合式电磁作动器实物如图7所示。

图7 复合式电磁作动器实物图Fig.7 Physical figure of the composite electro-magnetic actuator

3 复合式电磁作动器特性试验

对设计的复合式电磁作动器的力学特性及馈能特性进行台架试验，搭建的试验系统如图8所示。该复合式电磁作动器特性试验系统主要由激振台、控制及数据采集上位机、电机驱动器、电机电源、程序控制电流源、位移及力传感器等组成。激振台上下固定时，可进行主动出力静态特性试验，上端锁定、下端正弦激励可分别对作动器和MRD的特性进行动态试验。

图8 复合式电磁作动器特性试验系统Fig.8 Characteristic test system of the composite electro-magnetic actuator

3.1 基础阻力

复合式电磁作动器基础阻力主要由机械摩擦阻力和MRD基础阻尼力组成，均为不可控力，分别测量自供能复合式电磁作动器在速度为0.05 m/s、0.1 m/s、0.3 m/s和0.52 m/s下的拉伸方向和压缩方向基础阻力，结果如图9所示。

由图9可知：①复合式电磁作动器拉伸和压缩方向的基础阻力基本对称，且呈非线性分布，速度较小时，基础阻力增长较快，大于0.1 m/s之后，增长趋缓；②最大相对运动速度0.52 m/s时，拉伸方向的最大基础阻力为475.25 N，小于设计目标值500 N，满足要求。

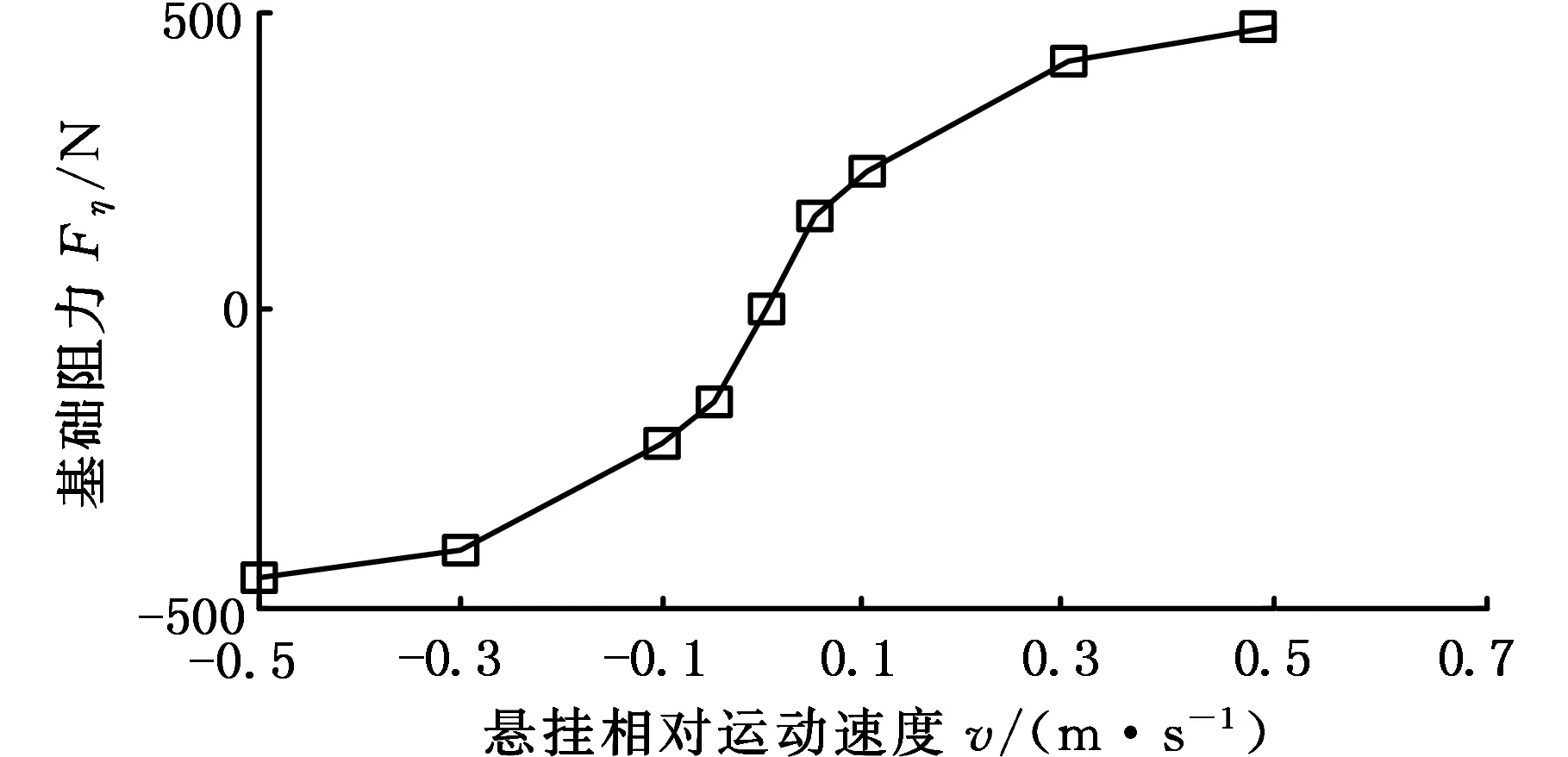
图9 复合式电磁作动器基础阻力Fig.9 Base resistance of composite electro-magnetic actuator

3.2 主动出力特性

激振台锁定不动，通过电机驱动器调试上位机发出的控制指令，对馈能式电磁作动器施加±0.2 A、±0.5 A、±1 A、±2 A、±3 A、±4 A、±5 A和±6 A的电流，测量相应条件下拉伸方向和压缩方向作动器出力的大小，将测得的试验数据与理论值进行比较，复合式电磁作动器的主动出力特性如图10所示。

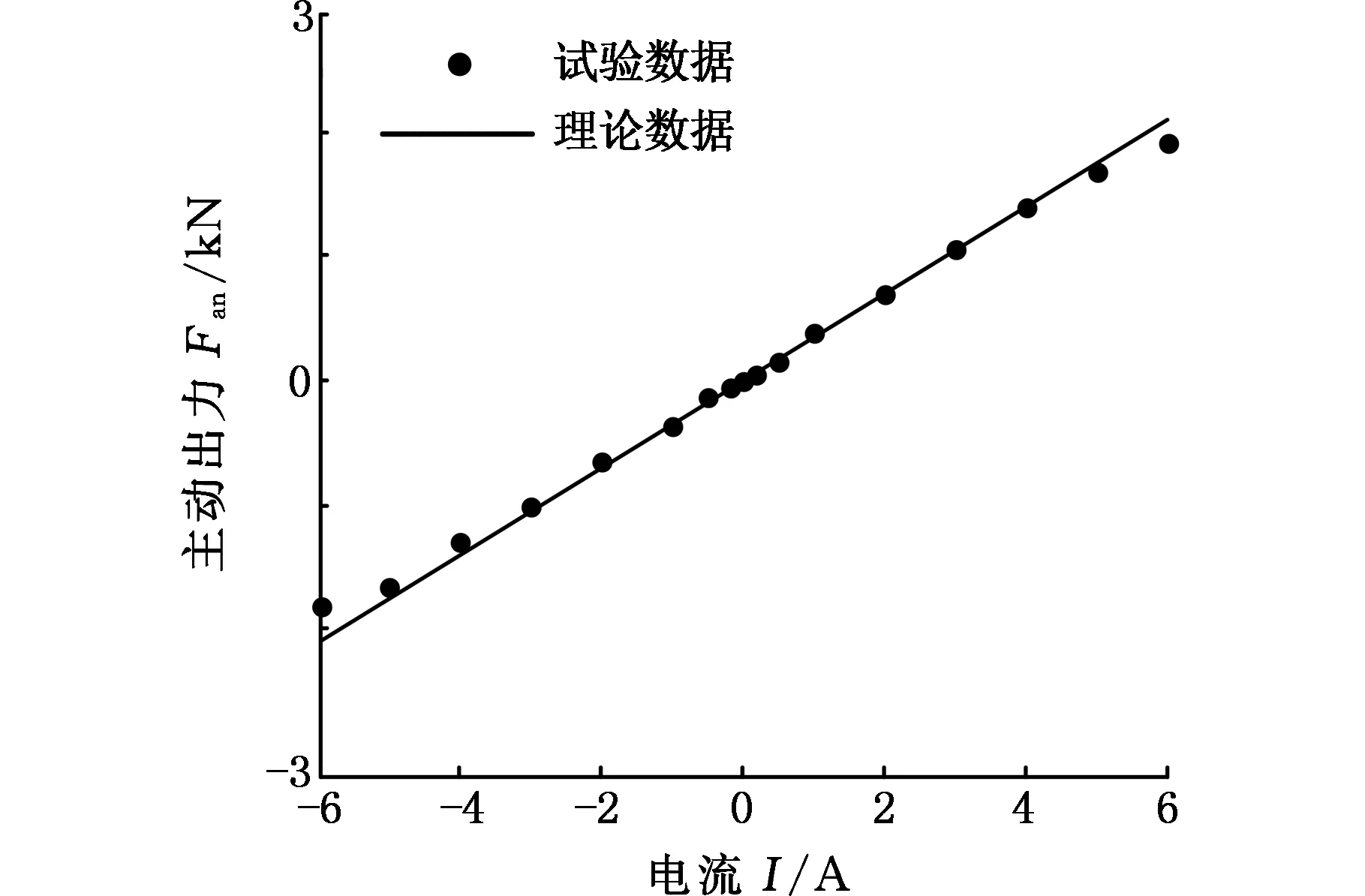
图10 复合式电磁作动器的主动出力特性Fig.10 Active output characteristics of the electro-magnetic actuator

由图10可知：①复合式电磁作动器主动出力与其驱动电流基本成线性关系，说明电机的电磁感应效率较高；②拉伸及压缩方向主动出力大小具有对称性；③电流小于3 A时，试验数据与理论数据基本上相符，大于3 A时，试验数据略小于理论数据；④复合式电磁作动器额定出力约为669 N，当电机驱动电流过载3倍状态工作时，其最大出力约为1 930 N，额定出力及峰值出力均大于设定目标值，满足设计要求。

3.3 馈能特性

输出电压测试原理图见图11，作动器上端固定，下端通过激振头带动实现正弦运动，电机输出电压经整流桥后与外接滑动变阻器相连，用电压计测量滑动变阻器两端电压值并记录。电机等效内阻3 Ω，外接电阻20 Ω，采用桥式整流电路，忽略压降，分别在0.1 m/s、0.2 m/s、0.3 m/s、0.4 m/s和0.52 m/s速度条件下测量反馈电压值，结果如图12所示。

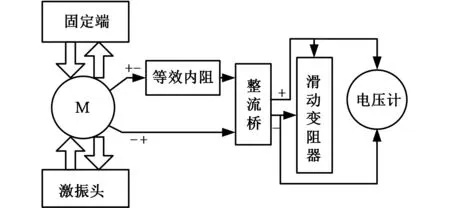
图11 输出电压测试原理图Fig.11 The principle diagram of the test of output voltage

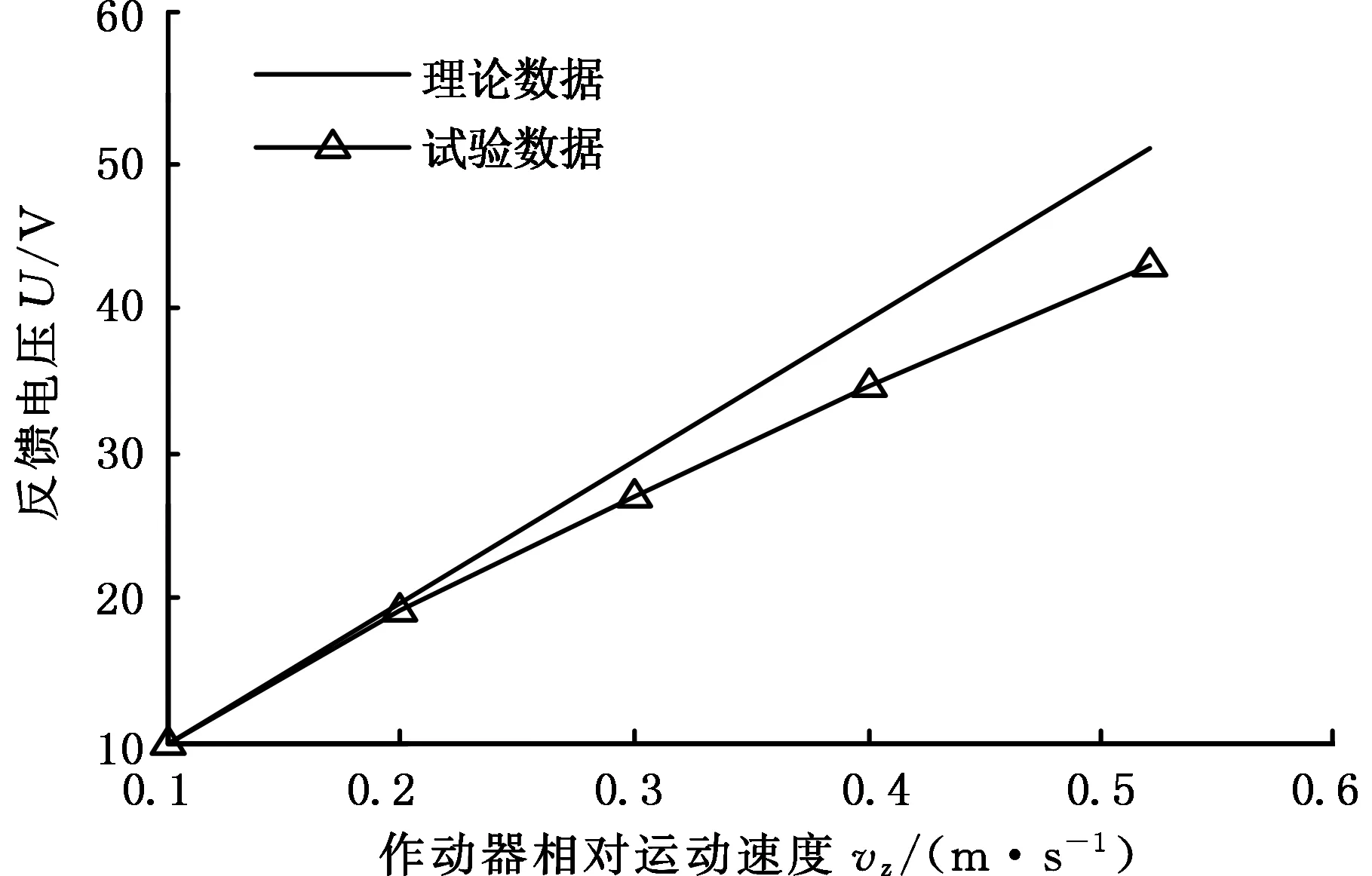
图12 复合式电磁作动器的反馈电压特性Fig.12 Feedback voltage characteristic of the composite electro-magnetic actuator

由图12可知：①反馈电压与相对运动速度基本成线性关系，与主动出力特性一致，表明电机的反馈电压特性较稳定；②随着相对运动速度的增加，反馈电压值比理论值略有下降，这与其基础阻力特性有关；③0.52 m/s相对运动速度时，反馈电压43 V，馈能特性较好。

3.4 MRD示功特性

实际行车条件下，悬挂相对运动速度通常在0.2 m/s以下，将相对运动速度设为0.1 m/s，分别测量电流为0、0.5 A、1.0 A、1.5 A及2.0 A时的输出阻尼力，复合式电磁作动器MRD部分的示功特性如图13所示。

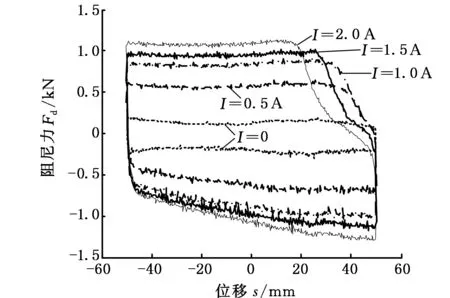
图13 复合式电磁作动器MRD部分的示功特性Fig.13 Indicator characteristics of MRD part of the composite electromagnetic actuator

由图13可知：①示功曲线所包围的面积表示MRD的耗功能力，MRD耗功能力随着电流的加大而增大；②最大电流2 A时，拉伸方向最大阻尼力1 100 N(拉伸为正)，压缩方向阻尼力随位移不同有所变化，最大1 250 N，而电流为0时，基础阻尼力约180 N，则可调库仑阻尼力约为920 N，可调倍数约为6，可调阻尼力略小于设计值，可调倍数大于设计值，符合设计要求；③示功曲线右上角出现“凹陷”现象，且随着电流加大越来越明显，这是由于单筒单出杆式MRD需要补偿装置补偿由于活塞两侧非对称引起的体积差，说明此时补偿气室压力略小，通过加大气室压力可以一定程度上减小“凹陷”程度。

4 结论

(1)该复合式电磁作动器包含电机和MRD两部分，根据各自特点可实现4种不同工况，半主动有馈能工况下可同时实现半主动控制减振及电机作发电机馈能，解决了减振及馈能之间存在的矛盾，此外，该作动器还具备“失效-安全”特性，提高了系统可靠性。

(2)该复合式电磁作动器最大主动出力1 930 N，悬挂相对运动速度0.52 m/s条件下可实现最大馈能电压43 V，MRD部分最大阻尼力1 100 N，可调倍数约为6，具备较好的力学特性及馈能特性，是一种较为理想的减振及馈能装置。

(3)由于机械加工及材料性能差异等原因，该复合式电磁作动器试验结果与理论计算略有差异，但该方案总体可行，通过优化设计尺寸和提高加工精度可进一步提高其性能。此外，由于该复合式电磁作动器由两个部件组成，基础阻力比一般减振器大，若要提高减振及馈能的效果，需要比一般减振系统稍高的激振频率和幅度，因此，实车试验时应尽量选择越野路面。

[1] 周长城. 车辆悬架设计及理论[M].北京：北京大学出版社，2011.

ZHOU Changcheng. Vehicle Suspension Design and Theory[M]. Beijing:Peking University Press,2011.

[2] ZHANG Peisheng. Design of Electromagnetic Shock Absorbers for Energy Harvesting from Vehicle Suspensions[D]. New York: Stony Brook University,2010.

[3] 王艳阳. 基于轮边驱动电动车的馈能型悬架综合性能研究[D]. 重庆：重庆大学，2014.

WANG Yanyang. Energy-regenerative Suspension Control Based on In-wheel Motored Vehicle[D]. Chongqing: Chongqing University,2014.

[4] 张进秋，张磊，罗涛，等. 车辆悬挂复合式电磁作动器设计及试验[J]. 装甲兵工程学院学报，2015,29(1):30-35.

ZHANG Jinqiu, ZHANG Lei, LUO Tao, et al. Design and Experiment Research of Compound Electromagnetic Actuator of Vehicle Suspensions[J]. Journal of Academy of Armored Force Engineering,2015,29(1):30-35.

[5] LIU Songshan, WEI Hao, WANG Weihua. Investigation on Some Key Issues of Regenerative Damper with Rotary Motor for Automobile Suspension[C]//International Conference on Electronic & Mechanical Engineering and Information Technology. Harbin,2011:1435-1439.

[6] 于长淼, 王伟华, RAKHEJA S, 等. 双超越离合器式电磁馈能阻尼器原型机试验测试与分析[J]. 吉林大学学报(工学版),2012,42(2):292-297.

YU Changmiao, WANG Weihua, RAKHEJA S, et al. Experiment and Analysis of the Dual-overrunning Clutches Electro-mechanical Regenerative Damper Prototype[J]. Journal of Jilin University(Engineering and Technology Edition),2012,42(2):292-297.

[7] NAKANO K, SUDA Y. Combined Type Self-powered Active Vibration Control of Truck Cabins [J]. Vehicle System Dynamics,2004,41(6):449-473.

[8] 郑玲，牛伯瑶，李以农，等. 基于遗传算法的汽车磁流变减振器多目标优化[J]. 汽车工程，2016,38(7):871-877.

ZHENG Ling, NIU Boyao, LI Yinong, et al. Multi-objective Optimization of Vehicle MR Damper Based on Genetic Algorithm[J]. Automotive Engineering,2016,38(7):871-877.

[9] 董小闵，于建强，杨茂举. 考虑温度因素的磁流变减振器的优化设计与实验[J]. 振动与冲击，2016,35(8):54-59.

DONG Xiaomin, YU Jianqiang, YANG Maoju. Optimization and Experimental Study of Magneto-rheological Fluid Damper Considering Temperature Effects[J]. Journal of Vibration and Shock,2016,35(8):54-59.

[10] HUANG B, HSIEH C Y, GOLNARAGHI F, et al. Development and Optimization of an Energy-regenerative Suspension System under Stochastic Road Excitation[J]. Journal of Sound and Vibration,2015,357:16-34.