考虑磨损误差的端齿盘分度精度的动态可靠性及灵敏度研究

王新刚 张 恒 王宝艳 皇甫一樊

东北大学机械动力学与可靠性研究中心，秦皇岛,066004

0 引言

端齿盘是数控机床刀架系统中的关键部件，其分度精度决定刀架的转位精度，进而影响机床的加工精度。国内外众多学者虽然对数控机床的可靠性进行了大量的研究，并证明了数控机床失效时间的数据分布类型满足威布尔分布或指数分布[1-5]，但目前对动力伺服刀架端齿盘分度精度可靠性灵敏度技术的研究还比较少。文献[6]通过对端齿盘齿根轮廓曲线的优化，提出了一种提高端齿盘可靠性的设计方法。文献[7]对端齿盘齿廓形状的数学模型进行研究，对端齿盘齿面轮廓方程进行推导，并对端齿盘的加工过程进行了计算机仿真分析。文献[8]对多齿分度台的互研过程进行建模和仿真，给出了齿盘分度误差的形成机理及多种换位方法对于齿盘分度误差的影响。目前国内外学者对提高端齿盘可靠性的研究主要通过分析其工作机理、齿面接触强度以及设计更加合理的几何参数来实现。本文对端齿盘中的加工误差和齿厚的磨损误差进行分析，建立端齿盘分度精度可靠性的数学模型，并应用摄动法和可靠性设计理论，结合灵敏度技术给出端齿盘的可靠度及可靠性灵敏度的计算方法。

1 齿盘误差分析

加工误差和齿厚的磨损误差对端齿盘的分度精度影响很大。本文结合几类常见的齿盘加工误差和端齿盘齿厚磨损误差进行端齿盘的分度精度误差分析。

1.1 齿厚磨损误差

齿厚误差是实际齿厚和标准齿厚的差值。齿厚误差会随着端齿盘在加载和卸载过程的累积作用时间的增加而逐渐增大。端齿盘的齿厚磨损是由端齿盘两齿面接触部分的相对滑动引起的，如图1所示。根据磨损理论，这种磨损属于黏着磨损。本文采用改进后的Archard方程来计算齿厚这一随机参量的磨损量。用A表示端齿盘在锁紧并加载或刚要卸载的过程中两啮合齿的表面接触区域面积，则端齿盘一个齿的磨损深度

(1)

式中，K为线性磨损量；F为摩擦副元素之间的法向载荷；L为零件间的相对滑动距离；H为较软材料的屈服极限值。

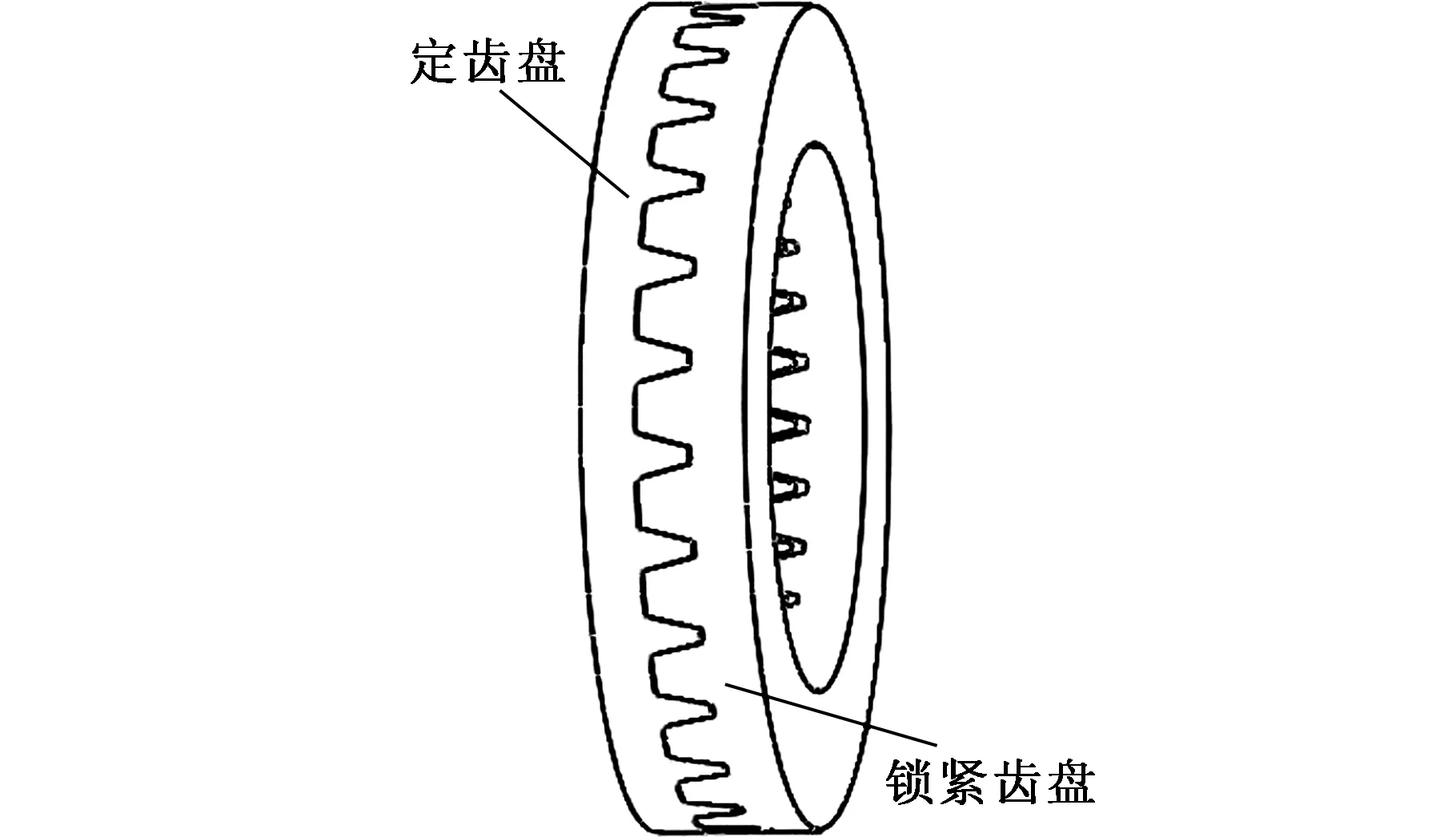
图1 齿厚误差示意图Fig.1 Schematic diagram of tooth thickness error

在动力伺服刀架的锁紧并加载或松开的过程中，两接触齿面会产生弹性变形和相对滑动。两接触齿面的压力

F=AEε

(2)

式中，ε为应变；E为弹性模量。

在动力伺服刀架加工工件的加载过程结束或刚要卸载时，由于端齿盘除受锁紧力外还会受到切向力的作用，所以对接触齿进行受力分析可得压力

(3)

式中，Fy为端齿盘锁紧力；Fτ为切向力；z为端齿盘齿数；γ为压力角。

在端齿盘受载过程中，定齿盘齿厚的正常变形

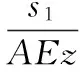
(4)

锁紧齿盘齿厚的正常变形

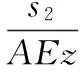
(5)

式中，s1为定齿盘齿厚；s2为锁紧齿盘齿厚。

在端齿盘受载过程中，两个端齿盘总的相对滑动距离

(6)

参照文献[9]的方法可以得到端齿盘一个加载或松开的工作过程中总的齿厚磨损量

(7)

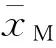
(8)

所以由端齿盘齿厚磨损所产生的分度误差

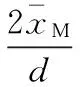
(9)

式中，d为端齿盘外径。

1.2 齿向误差

理论齿向线和实际齿向线间的转角为齿向误差。图2所示(从节平面将齿盘剖开)为端齿盘节平面上的齿向误差情况。

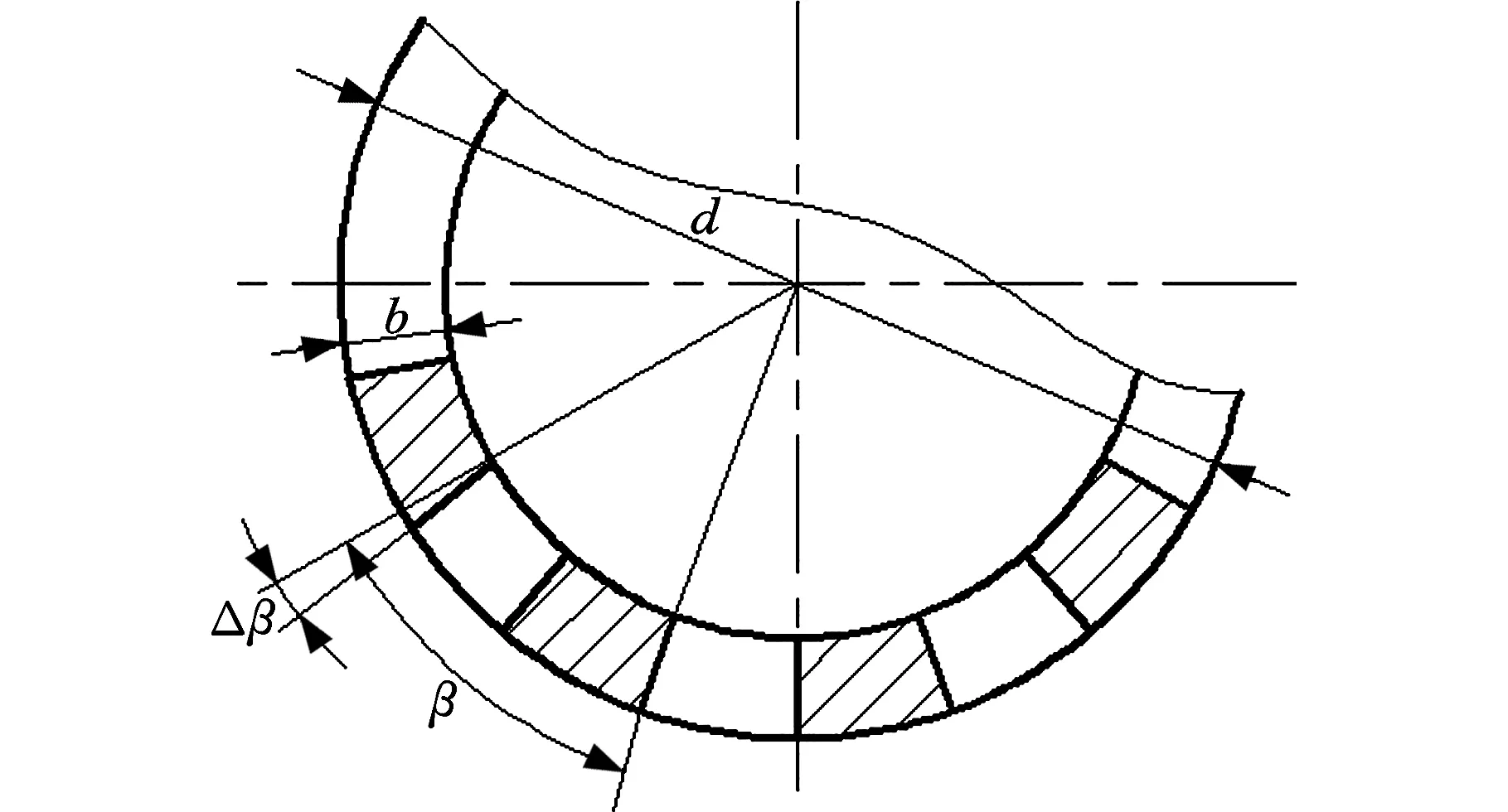
图2 齿向误差示意图Fig.2 Schematic diagram of tooth direction error

由文献[10-11]可得由齿向误差引起的分度误差

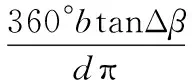
(10)

式中，b为齿宽；Δβ为齿盘接触齿面齿向误差。

1.3 齿形半角误差

端齿盘实际齿形半角和标准齿形半角的偏差为齿形半角误差，用Δα/2表示。如图3所示，设端齿盘啮合时左右齿盘的齿中线彼此对准，左齿盘的齿为标准齿形半角，右齿盘的齿有齿形半角误差Δα/2，标准齿形角为θ。由文献[10-11]可得由齿形半角误差引起的分度误差

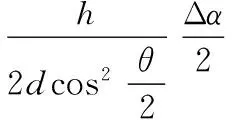
(11)

式中，h为齿的工作高度。

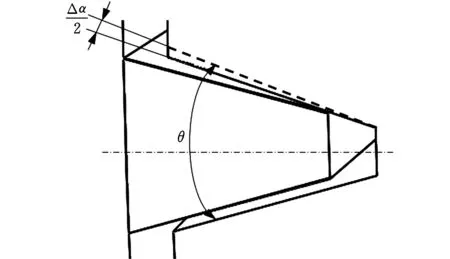
图3 齿形半角误差示意图Fig.3 Schematic diagram of half angle error of tooth

1.4 齿盘总的分度误差

由齿盘的齿厚磨损误差、齿向误差、齿形半角误差可以得到齿盘总的分度误差

(12)

2 齿盘分度精度可靠性设计

齿盘的分度误差需在允许范围内，即

|Δφ|≤τ

(13)

式中，τ为端齿盘允许分度误差。

为了使端齿盘分度时满足上述要求，端齿盘分度误差所对应的极限状态函数分别为

gu(X,t)=τ-Δφ(X,t)

(14)

gm(X,t)=τ+Δφ(X,t)

(15)

将齿盘分度时的分度精度可靠性可分为两种状态进行研究，即当齿盘的分度误差满足Δφ≥-τ时的可靠度Rm和齿盘的分度误差满足Δφ≤τ时的可靠度Ru，然后可以求出齿盘总的分度精度可靠度

R=Rm+Ru-1

(16)

由于篇幅所限，本文只讨论齿盘的分度误差满足Δφ≤τ时的可靠度。由式(12)及上述分析可得动力伺服刀架端齿盘分度误差极限状态方程：

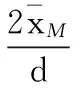
(17)

基本随机变量的向量X=(Fy,Fτ,γ,A,s1,s2,b,Δβ,d,h,Δα/2)T。运用二阶矩和摄动方法[12-13]，对刀架齿盘进行可靠性设计。对应于输出分量Δφ的可靠度可以定义为

(18)

(19)

式中，fX(X,t)为基本随机参数向量X的联合概率度函数；gu(X,t)为状态函数，可表示动力伺服刀架端齿盘分度精度的两种状态。

动力伺服刀架端齿盘分度误差极限状态函数的均值方差可以做如下定义。将随机参量向量X和状态函数gu(X)表示为

X=Xd+εXr

(20)

gu(X,t)=gud(X,t)+εgur(X,t)

(21)

式中，ε为一个小参数；下标r表示随机参量中的随机部分，且其具有零均值；下标d表示随机参量中的确定部分。

对式(20)、式(21)求数学期望可得

(22)

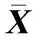
(23)

同理，可对随机参量向量X和状态函数gu(X)取方差，并根据随机分析理论[14]可得

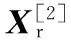
(24)

var(gu(X,t))=E((gu(X,t)-E(gu(X,t)))[2])=
ε2E((gur(X,t))[2])

(25)

其中，var(X)为随机参量的方差矩阵，((X-E(X))[2]=(X-E(X))⊗(X-E(X))，为Kronecker幂，符号⊗为Kronecker积。根据矩阵值函数和随机向量值的Taylor展开式，可以把gur(X)在E(X)=Xd处展开到一阶为止，有

(26)

把式(26)代入式(25)中可得

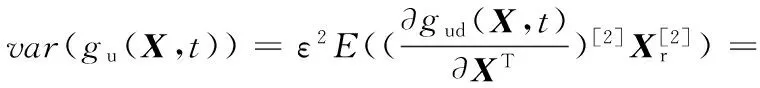
(27)

基本随机变量的均值E(X)和方差var(X)是已知的，可以得到可靠性指标

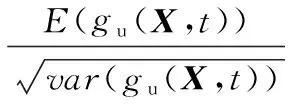
(28)

利用可靠性指标βu可以得到动力伺服刀架端齿盘的分度精度可靠度

Ru=Φ(βu)

(29)

式中，Φ(·)为标准正态分布函数。

3 端齿盘的可靠性灵敏度设计

动力伺服刀架端齿盘分度精度可靠度对其基本参数向量的均值和方差的灵敏度[15]为

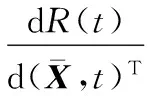
(30)

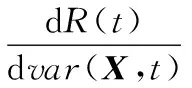
(31)

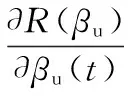
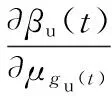
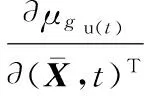
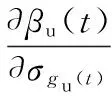
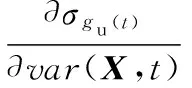
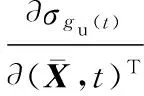
式中，ψ(βu(t))为正态分布的概率密度函数；In为n×n维的单位矩阵；Un×n为n2×n2维的矩阵。

把已知条件和可靠度计算结果代入式(30)和式(31)，可以获得可靠度Ru对基本随机变量X的均值和方差的灵敏度矩阵。

4 数值算例

某型号的刀架齿盘各参量的均值和标准差如下：允许精度误差τ=2.7142×10-3rad，齿数z=24，线性磨损量K=4.5×10-4,较软材料的屈服极限值H=685 MPa,弹性模量E=206 GPa, 啮合齿表面接触区域面积A=(148.46，0.74)mm2(括号里为该量的均值和标准差，以下类同),端齿盘锁紧力Fy=(56520，282.6)N, 切向力Fτ=(2215.4，21.1)N,压力角γ=(0.52，0.0028)rad，定齿盘齿厚s1=(6.98，0.035)mm,锁紧齿盘齿厚s2=(17.22，0.086)mm,端齿盘的标准齿形角θ=0.52 rad,齿宽b=(0.07，3.5×10-5)m，齿盘外径d=(0.140，1.1×10-4)m，接触齿面齿向角误差Δβ=(0，0.0013)rad，齿形半角误差Δα/2=(0，0.0026)rad，齿的工作高度h=(7.5，0.0375)mm。

将齿盘各结构参数数据代入式(28)、式(29)可得图4所示的动力伺服刀架端齿盘的分度精度的动态可靠性曲线。从图4中可以看出，端齿盘的分度精度可靠度随加载和卸载过程的累积作用时间的增加而逐渐降低。

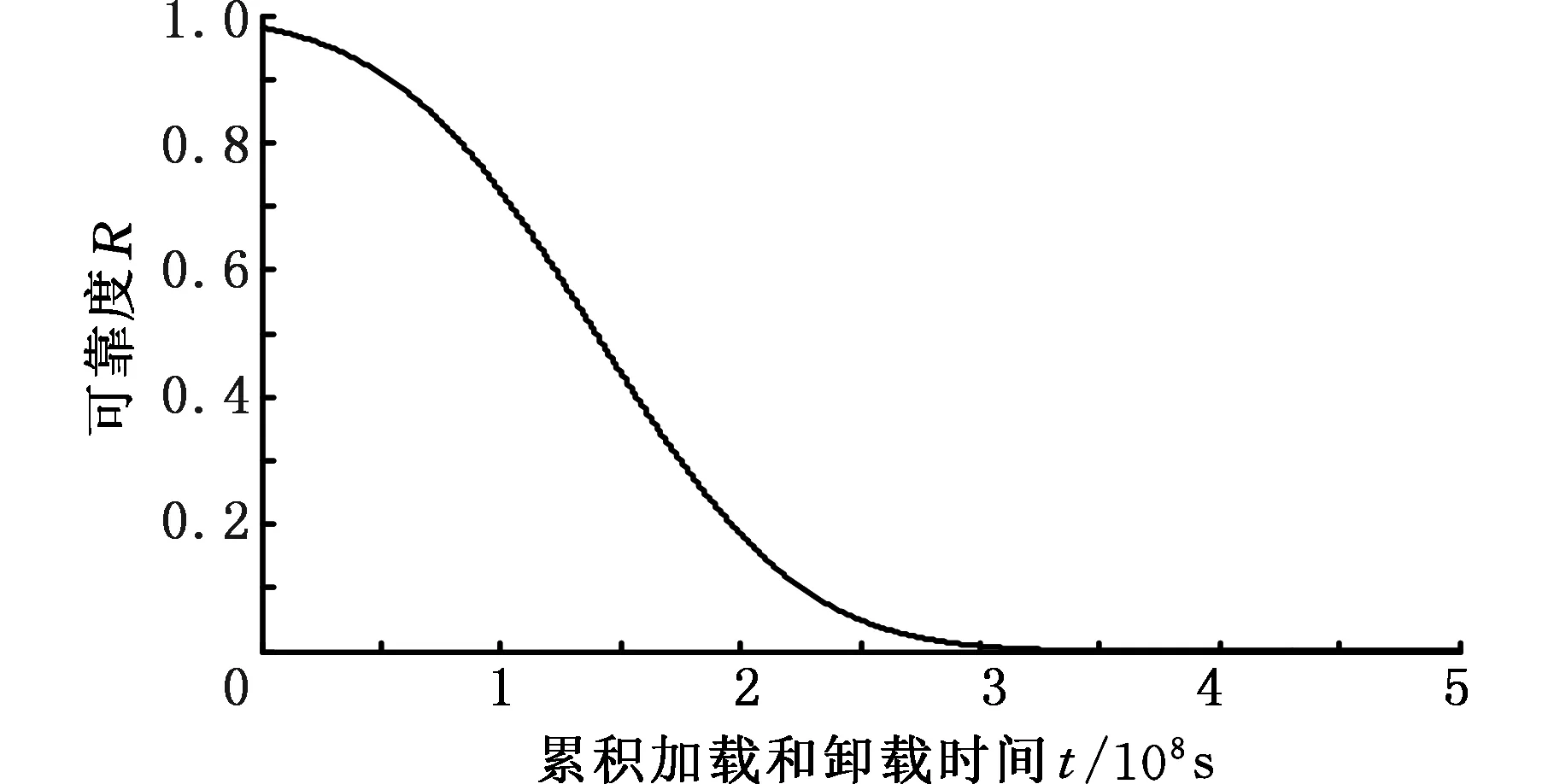
图4 动力伺服刀架端齿盘分度精度可靠度曲线Fig.4 Indexing accuracy reliability curve of the end-toothed disc of power servo tool rest

由于可靠度是随着时间不断变化的，所以可靠度对各参数的灵敏度也应该是一个随着时间变化的动态量。由式(30)、式(31)可以得到图5、图6所示的各设计参数向量的均值和方差的灵敏度动态曲线。

由图5可以看出，一些基本参数向量的均值灵敏度始终是小于零的，这些参数包括锁紧力Fy、切向力Fτ、定齿盘齿厚s1、锁紧齿盘齿厚s2、接触齿面齿向误差Δβ、齿形半角误差Δα/2。随着动力伺服刀架加载和卸载过程作用时间的累积，这几个基本参数向量的灵敏度具有先减小后增大的趋势。基本随机参数向量齿宽b和齿的工作高度h的均值灵敏度为零，这与其均值有关。其他基本参数向量的均值灵敏度都是先减小到负的最大，后逐渐增加到正的最大，最后减小到零。由图6可以看出，基本随机参数齿宽b和齿的工作高度h的方差灵敏度一直为零，而其他基本参数的方差灵敏度都是先减小到负的最大，后逐渐增加到正的最大，最后减小到零。

通过上述分析可将一些基本参数进行优化以提高齿盘的分度精度可靠性。受实际的加工条件、刀架及刀具结构的限制，经可靠性优化设计后，啮合齿表面接触区域面积A=(158.23，0.74)mm2，齿向误差Δβ=(0，0.00085)rad，定齿盘齿厚s1=(6.56，0.035)mm, 锁紧齿盘齿厚s2=(16.32，0.086)mm。得到图7所示优化后的可靠度变化规律。从图7中可以看到，优化后的齿盘的分度精度在有效使用寿命内的可靠度较原来有所提高。

5 结论

(1)受端齿盘加工误差和齿厚磨损误差的影响，动力伺服刀架分度精度可靠度随加载和卸载过程的累积作用时间的增加有逐渐减小的趋势。

(a)Fy (b)Fτ (c)γ (d)A

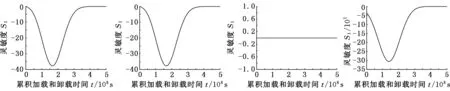
(e)s1 (f)s2 (g)b (h)Δβ

(i)d (j)h (k)Δα/2 图5 端齿盘各随机变量期望的分度精度可靠性灵敏度曲线Fig.5 Indexing accuracy reliability sensitivity curve of the random variables’ mean of the end-toothed disc

(a)Fy (b)Fτ (c)γ (d)A

(e)s1 (f)s2 (g)b (h)Δβ

(i)d (j)h (k)Δα/2 图6 端齿盘各随机变量方差的分度精度可靠性灵敏度曲线Fig.6 Indexing accuracy reliability sensitivity curve ofthe random variables’ variance of the end-toothed disc

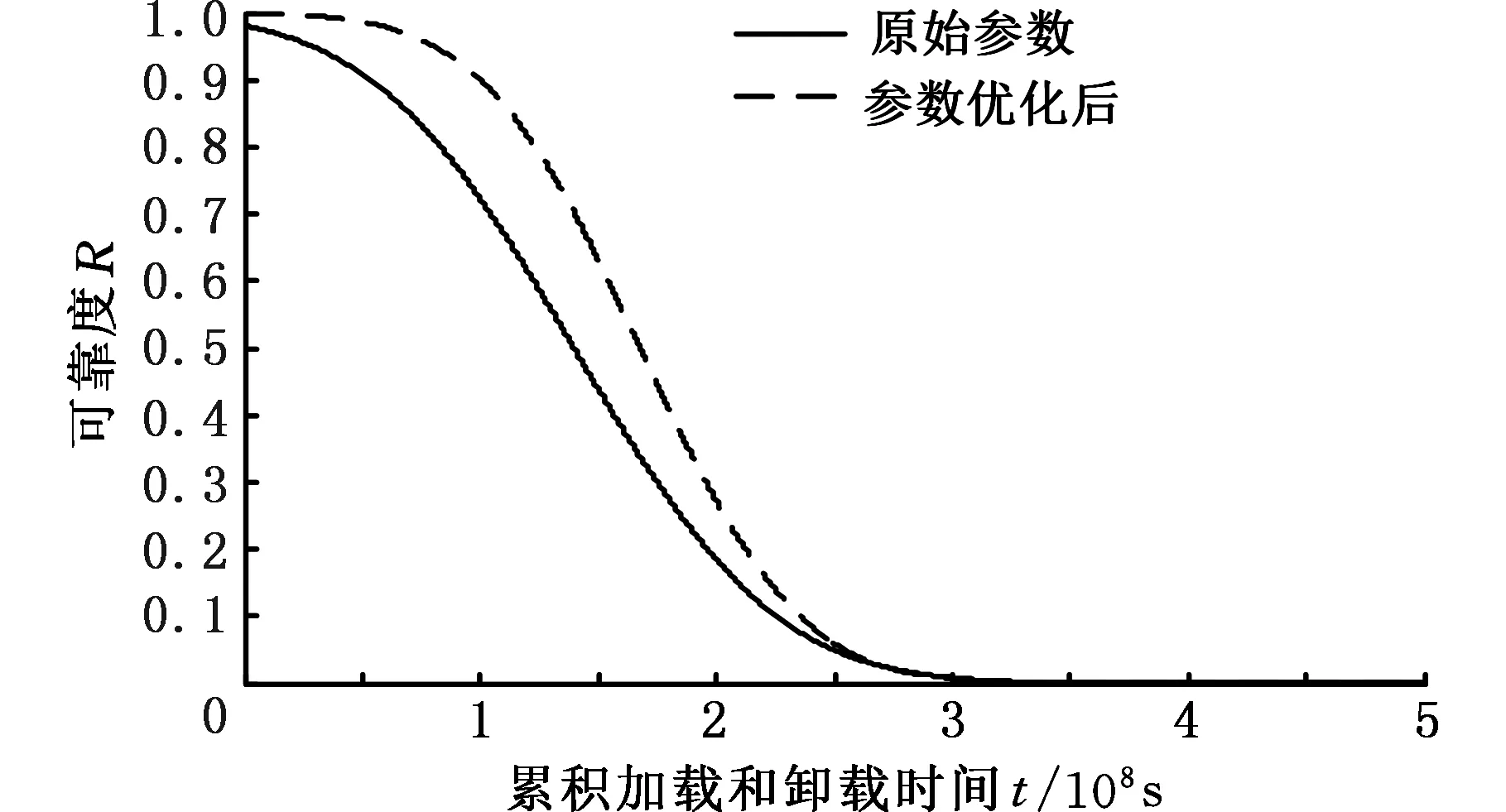
图7 动力伺服刀架端齿盘分度精度可靠度曲线Fig.7 Indexing accuracy reliability curve of the end-toothed disc of power servo tool rest

(2)通过对各基本参量的期望和方差的动态可靠性灵敏度变化曲线进行分析可知：在动力伺服刀架端齿盘的设计或使用过程中可以适当减小切向力、锁紧力、接触齿面齿向误差、齿形半角误差、定齿盘齿厚和锁紧齿盘齿厚的值来提高分度精度可靠度。通过优化啮合齿表面接触区域面积、定齿盘齿厚、锁紧齿盘齿厚和齿向误差参数，可以提高动力伺服刀架分度精度的可靠度。

[1] WANG Z M, YANG J G, WANG G, et al. Application of Three-parameter Weibull Mixture Model for Reliability Assessment of NC Machine Tools: a Case Study [J]. Proceedings of the Institution of Mechanical Engineers, Part C：Journal of Mechanical Engineering Science,2011,225(C11):2718-2726.

[2] WANG Zhiming, YANG Jianguo. Reliability Assessment of Numerical Control Machine Tools Using Weibull Mixture Models [J]. Advanced Materials Research,2011,181/182:161-165.

[3] JIA Yazhou, WANG Molin, JIA Zhixin. Probability Distribution of Machining Center Failures [J]. Reliability Engineering and System Safety,1995,50(1):121-125.

[4] MERRICK J R W, SOYER R, MAZZUCHI T A. A Bayesian Semiparametric Analysis of the Reliability and Maintenance of Machine Tools [J]. Technometrics,2003,45(1):58-69.

[5] WU Jun, DENG Chao, SHAO Xinyu, et al. A Reliability Assessment Method Based on Support Vector Machines for CNC Equipment [J]. Science in China Series E—Technological Sciences,2009,52(7):1849-1857.

[6] SANDEEP M J, SANDOVAL S R. Curvic Coupling Fatigue Life Enhancement through Unique Compound Root Fillet Design: US, US09905492 [P].2004-01-06.

[7] TSAI Y C, HSU W Y. A Study on the CAD/CAM of Curvic Couplings [J]. Manufacturing Materials and Metallurgy,2002,3B:1157-1162.

[8] 赵大泉, 张伯鹏, 郑力. 多齿分度台互研过程的建模与仿真[J]. 清华大学学报(自然科学版),2002,42(11):1459-1462.

ZHAO Daquan, ZHANG Bopeng, ZHENG Li. Modeling of the Abrasion of an End-tooth Dividing Table [J]. Tsinghua University, (Sci.&Tech.),2002,42(11):1459-1462.

[9] LI Changyou, WANG Wei, ZHANG Yimin, et al. Indexing Accuracy Reliability Sensitivity Analysis of Power Tool Turret [J]. Science and Technology,2015,17(1):27-34.

[10] 陈福东. 伺服/动力刀架端齿盘接触分析及分度误差研究[D]. 南京: 东南大学,2013.

CHEN Fudong. Study on Contact and Dividing Error of End-toothed Disc of a Servo/Dynamic Turret [D]. Nanjing: Southeast University,2013.

[11] 刘威. 基于多齿分度盘的精密分度与测角技术研究[D]. 西安：西北工业大学,2006.

LIU Wei. The Study on the High Dividing Accuracy and Angle Measurement Technique Based on the End-tooth Dividing Table [D]. Xi’an: Northwestern Polytechnical University,2006.

[12] ZHANG Yimin, HE Xiangdong, LIU Qiaolian, et al. Reliability Sensitivity of Automobile Components with Arbitrary Distribution Parameters [J]. Proceedings of the Institution of Mechanical Engineers Part D： Journal of Automobile Engineering,2005，219(D2):165-182.

[13] LYU Hao, ZHANG Yimin, ZHANG Xufang, et al. Reliability and Sensitivity of Bogie Frame of High-speed Train with Strength Degradation [J]. Journal of Central South University,2013,20:3490-3496.

[14] FAI Ma. Extension of Second Moment Analysis to Vector-valued and Matrix Valued Functions [J]. International Journal of Non-linear Mechanics,1987,22(3):251-260.

[15] ZHANG Yimin, ZHU Lisha, WANG Xingang. Advanced Method to Estimate Reliability-based Sensitivity of Mechanical Components with Strongly Nonlinear Performance Function [J]. Applied Mathematics and Mechanics (English Edition),2010,31(10):1325-1336.