一种3T1R并联机构设计及运动学性能分析

朱 伟 顾开荣 王传伟 刘晓飞

常州大学机械工程学院,常州,213164

0 引言

三平移一转动(3T1R)并联机构在高速抓放、自动分拣、生产线装配等领域具有广泛的应用需求。根据动平台转动轴线的不同，3T1R并联机构可分为三种形式：3T1Rx、3T1Ry、3T1Rz，即动平台可实现三维平动和分别绕x、y、z轴的转动。

由于DELTA机器人的三组支链采用相同的R(SS)2结构[1]，获得很好的应用效果，因此类似的平行四边形支链结构在3T1R并联机器人中得到广泛应用，这种机构具有高速和高加速度的操作性能。文献[2-5]先后发明了同属一类的由4条R(SS)2支链和双平台组成的3T1R并联机构(分别称为H4、I4、Par4和Heli4)。KIM等[6-7]采用RR(RR)2RR支链设计了两种全转动副3T1Rx、3T1Rz并联机构。汪满新等[8]采用4条R(UU)2支链设计了一种单平台3T1Rz机构。刘辛军等[9]将(SS)2支链改进为(SRRS)2，并发明了由4条R(SRRS)2R支链组成的3T1Rz并联机器人，即X4机构。

这类少自由度机构在运动过程中容易出现奇异位形，此时可能因失去刚度或失去部分自由度而变得不可控制，从而使机构的有效工作空间变小甚至不连续，在很大程度上影响了机构的运动性能[10]。在机构的适当位置添加冗余驱动支链，可以使机构避开奇异位形，同时可提高机构刚度，增大有效工作空间。

本文设计一种2R(SRS)2R+2R(SRS)2非对称3T1Ry型并联机构，运用方位特征理论[11]分析了机构自由度和拓扑结构，推导出机构的位置正反解方程，通过位置数值解对运动方程正确性进行验证。分析了机构的工作空间及奇异位形等运动性能指标，设计了一种新型冗余驱动方式，可有效消除部分正解奇异位形，且保持机构的可达工作空间不变。

1 机构拓扑结构分析

1.1 机构描述

2R(SRS)2R+2R(SRS)2并联机构由动平台、静平台及4条分支组成，三维模型如图1所示。每条支链中均包含一条主动臂AiBi和一个(SRS)2平行四边形结构，主动臂一端通过转动副Ri1与定平台相连，另一端与平行四边形结构短边的中心固定连接，平行四边形中的转动副Ri2//Ri3(i=1,2,3,4)，且轴线垂直于该平面。其中，第1、第3支链为平行的R(SRS)2R结构，竖直杆CiDi一端通过转动副Ri4(i=1,3)与动平台连接，另一端和平行四边形短边固定连接，且R11⊥R14，R14与R34同轴，R11//R31；第2、第4支链为平行的R(SRS)2结构，支链的平行四边形短边与动平台固定连接，R21//R41，结构原理如图2所示。

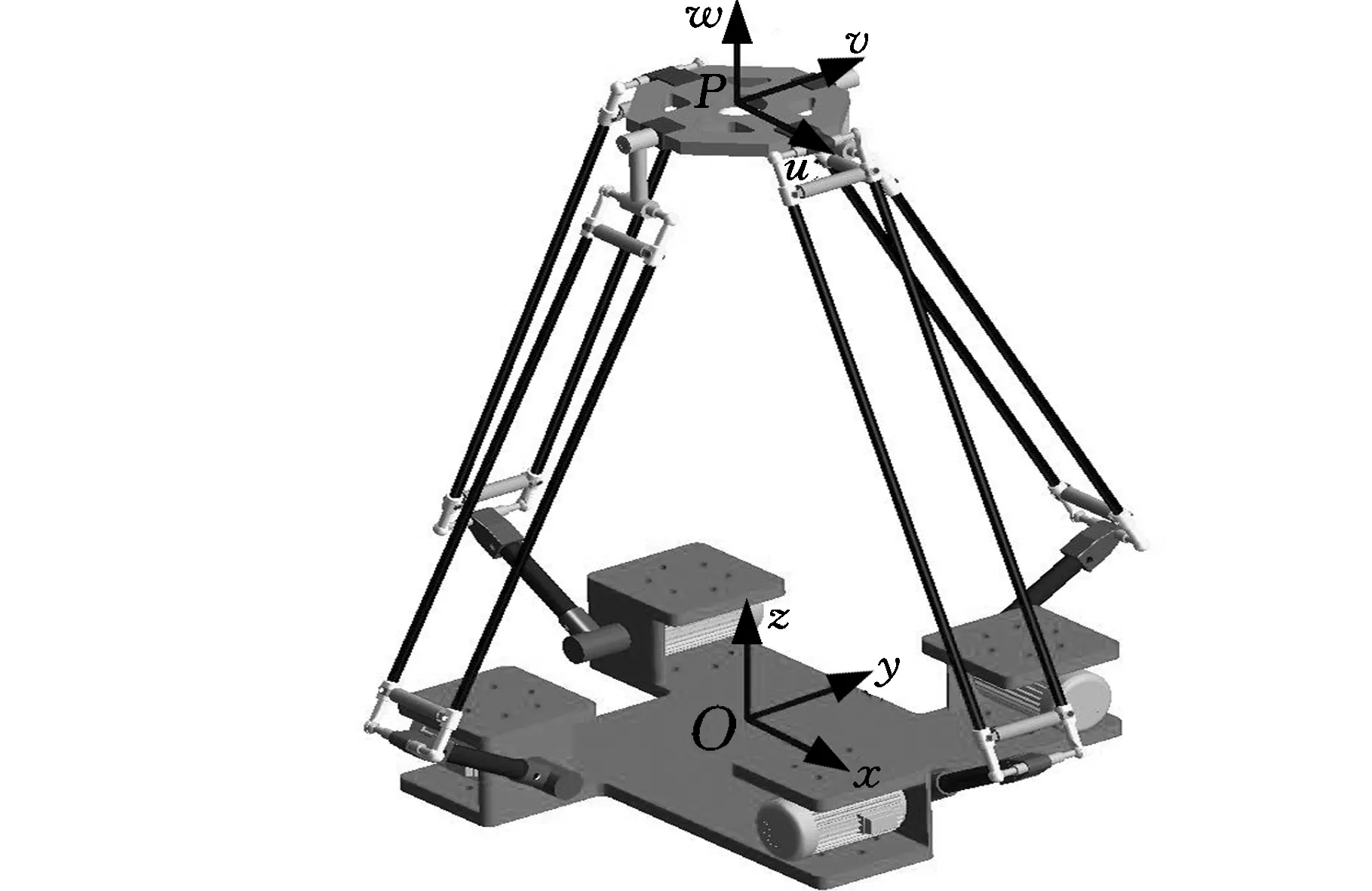
图1 机构三维模型Fig.1 3D model of the mechanism

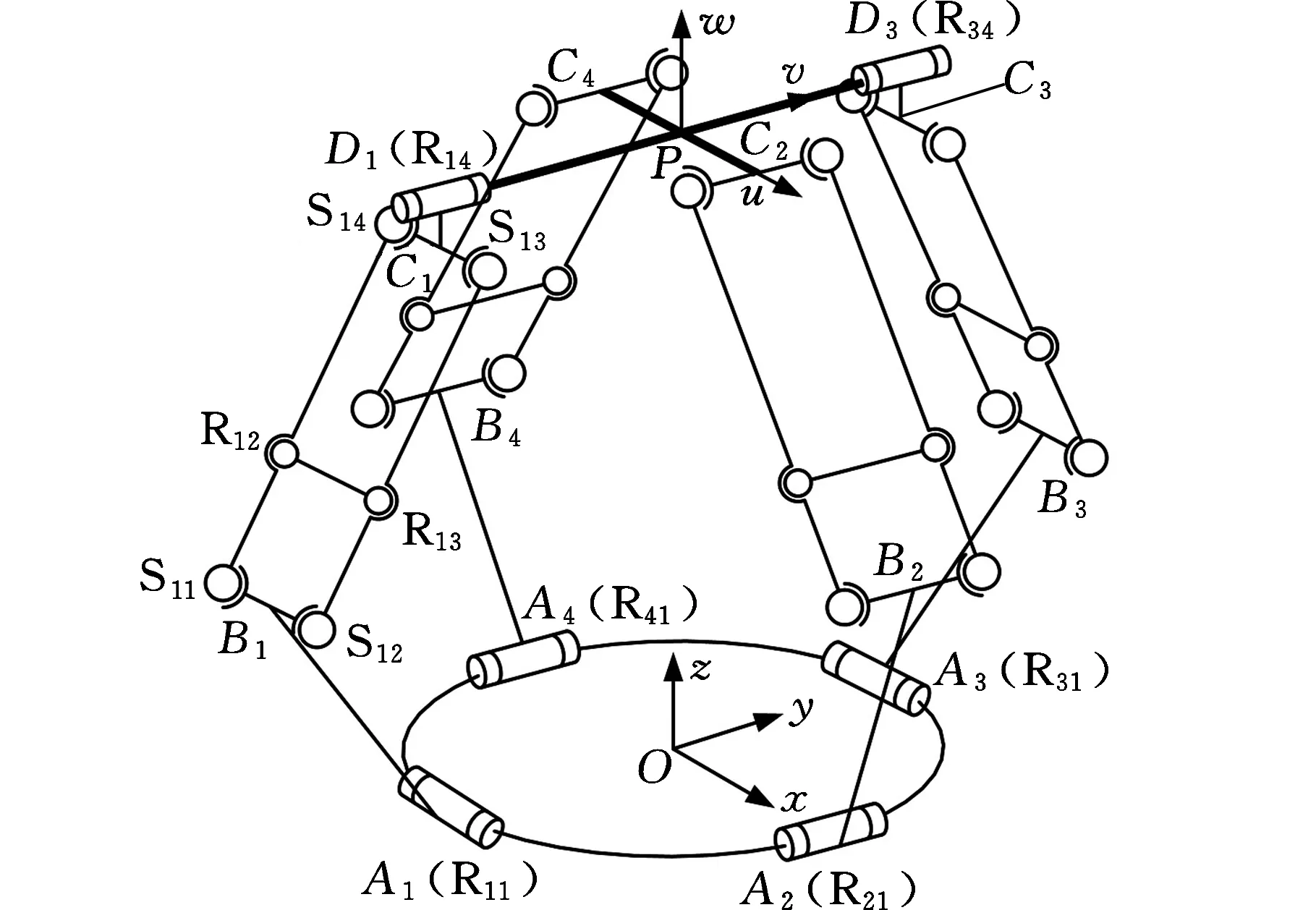
图2 机构原理图Fig.2 Schematic diagram of mechanism

机构采用非完全对称结构，每条支链中与静平台相连的转动副Ri1中心Ai位于半径为r的圆周上，动平台为长和宽分别为2m、2n的矩形，4条支链与动平台的连接点Ci、Di位于动平台4条边的中点。在静平台中心上建立定坐标系Oxyz，x轴沿OA2方向，y轴沿OA3方向，z轴垂直于静平台竖直向上；在动平台的中心P点建立动坐标系Puvw，u轴沿PC2方向，v轴沿PD3方向，w轴垂直于动平台向上，如图2所示。

1.2 机构拓扑结构分析

根据文献[11]提出的机构有序单开链结构组成原理：自由度(DOF)为F的并联机构(PM)可看成由F个驱动副和V个有序单开链(SOC)依次连接而成。图2中，机构可看成是由第2、第4支链构成的第1独立回路(记为子并联机构Mpa(2-4))、第1独立回路和第1支链构成的第2独立回路(记为子并联机构Mpa(1-2-4))以及第2独立回路和第3支链构成的第3独立回路(记为并联机构Mpa)依次连接而成。根据方位特征原理，机构的方位特征集(POC)可表示为

(1)

式中，V为独立回路数，V=3；Mbj为第j条支链的POC集,j=1,2,3;t、r分别表示POC集的移动和转动。

根据机构自由度计算公式：

(2)

式中，ξLj为第j个独立回路的独立位移方程数;q为运动副数目。

可见，该机构为3T1Ry运动输出机构。机构耦合度为

(3)

式中，Δj为第j个单开链的约束度。

机构的结构分解路线可表示为

PM[F=4,V=3,k=2]=J[4]+SOC1(Δ1=2)+

SOC2(Δ2=-1)+SOC3(Δ3=-1)

(4)

SOC1：{-A2-B2-C2-C4-B4-A4-}

SOC2：{-A1-B1-C1-D1-}

SOC3：{-A3-B3-C3-D3-}

2 机构位置分析

2.1 位置反解

根据图2中建立的坐标系，设机构动平台中心P点在定坐标系Oxyz中的坐标P=(xP,yP,zP)T，绕y轴的姿态角为α，4条支链中驱动副的输入角为θi(i=1,2,3,4)。各杆长分别为：AiBi=l1，BiCi=l2(i=1,2,3,4)，CiDi=h(i=1,3)，DiP=m(i=1,3)，CiP=n(i=2,4)。

点Ai、Bi在定坐标系Oxyz中的坐标为

动平台上各点在定坐标系Oxyz中的坐标为

(5)

R=rot(y,α)

式中，R为动坐标系Puvw相对与定坐标系Oxyz的旋转矩阵；mi为杆DiP的单位矢量；ni为杆CiP的单位矢量。

根据图2中矢量关系，可得封闭矢量方程

(6)

式中，ai为OAi的单位矢量；bi为杆AiBi的单位矢量；ci为杆BiCi的单位矢量;e为CiDi的单位矢量。

将各点坐标代入式(6)，整理后可得如下形式：

Eicosθi+Fisinθi+Gi=0i=1,2,3,4

(7)

E1=2l1(yP-m+r)F1=-2l1(zP-h)

E2=-2l1(xP+ncosα-r)

F2=-2l1(zP-nsinα)

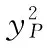
E3=-2l1(yP+m-r)F3=-2l1(zP-h)

E4=2l1(xP-ncosα+r)

F4=-2l1(zP+nsinα)

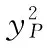
可求解出机构的反解方程

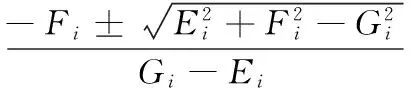
(8)

2.2 位置正解

根据上述拓扑结构分解顺序，采用序单开链法[12]求解机构的正解。

2.2.1单开链SOC1(Δ=2)

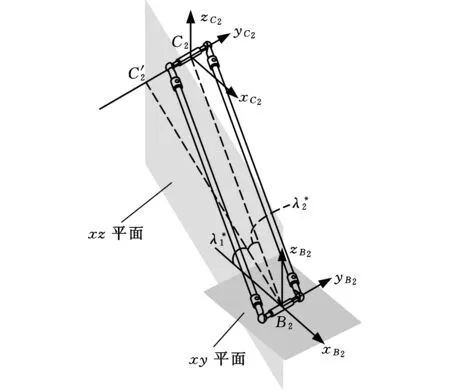
图3 虚拟变量位置示意图Fig.3 Diagram of dummy variables

易得C2点虚拟坐标为

(9)

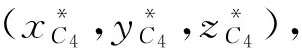
(10)

解之得

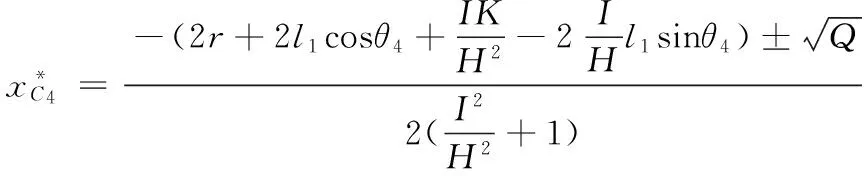
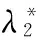
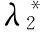
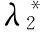
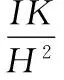
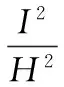
2.2.2单开链SOC2(Δ=-1)

因为P为C2C4中点，D1P平行于y轴，C1D1平行于z轴，所以第2单开链中C1的坐标为

(11)

根据杆长B1C1=l2的长度约束条件，得到相容方程:

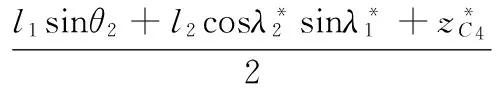
(12)

2.2.3单开链SOC3(Δ=-1)

因为P为C2C4中点，D3P平行于y轴，C3D3平行于z轴，所以第3单开链中C3的坐标为

(13)

根据杆长B3C3=l2的长度约束条件，得到相容方程:

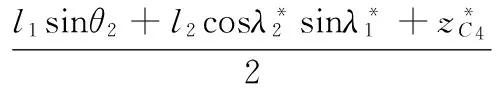
(14)

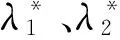
2.3 位置正反解的数值验证

选取该机构的结构参数为：r=50 mm，l1=60 mm，l2=90 mm，h=10 mm，m=50 mm，n=20 mm。为了验证机构的正反解，将动平台位姿参数代入反解方程式(8)，通过MATLAB编程算出机构输入参数，如表1所示。再将机构输入参数代入正解相容方程式(12)和式(14)，得到动平台位姿参数，如表2所示。从表1和表2可看出，动平台的位置正反解完全匹配。

表1 位置反解Tab.1 Inverse position analysis

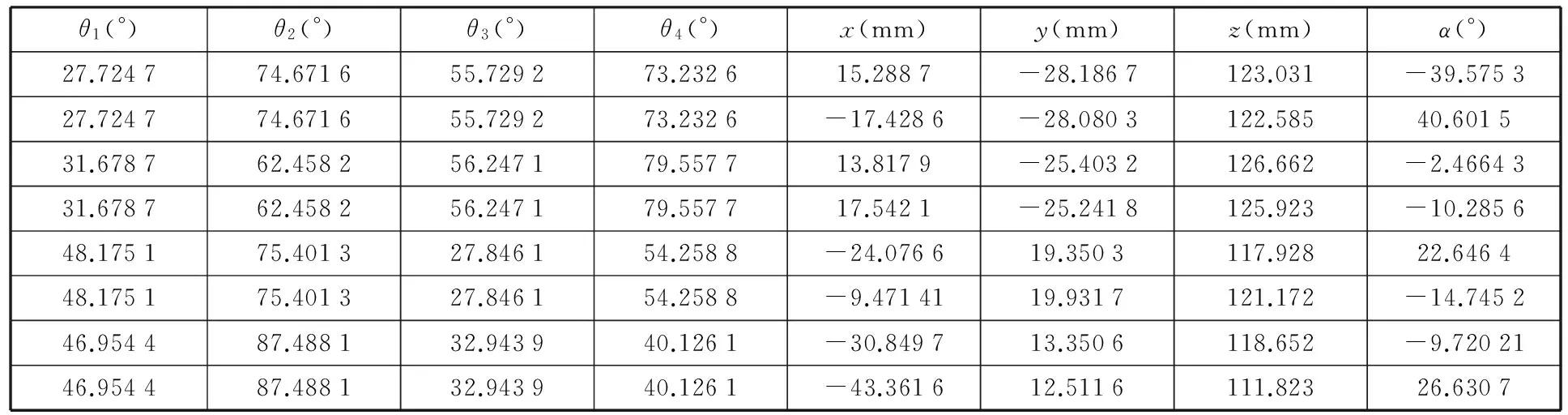
表2 位置正解Tab.2 Direct position analysis

3 机构运动性能分析

3.1 工作空间分析

本机构工作空间的主要约束条件包括杆长约束和运动副约束。设定4个驱动角θi(i=1,2,3,4)范围为-π～π。考虑到机构的有效工作空间，搜索高度设定为[20 mm,120 mm]。对于不同的工作运动要求，动平台处于不同姿态角时，机构的工作空间不同。图4所示为α分别为0°、30°、60°、90°、120°、150°定姿态时，机构的三维位移工作空间。可见，当α=0°时，可达工作空间范围最大，随着α增大,工作空间依次减小，α=150°时，可达工作空间最小。总体而言，机构在各姿态的可达工作空间连续性较好，当z≥60 mm时，机构工作空间几乎不出现空洞。在工作空间的下半部分，越往下，机构工作空间空洞越大，表示机构工作空间内部不可达区域增多，所以尽量避免机构在工作空间底部位置工作。

3.2 雅可比矩阵

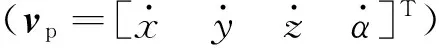
Jpvp=Jqvq

(15)

(16)

(17)

N11=2(yP-m+r+l1cosθ1)l1sinθ1+
2(zP-h-l1sinθ1)l1cosθ1

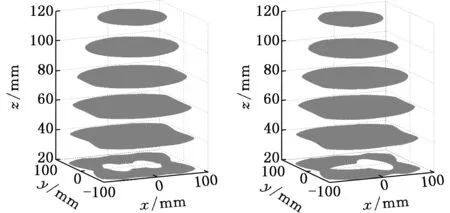
(a)α=0° (b)α=30°

(c)α=60° (d)α=90°

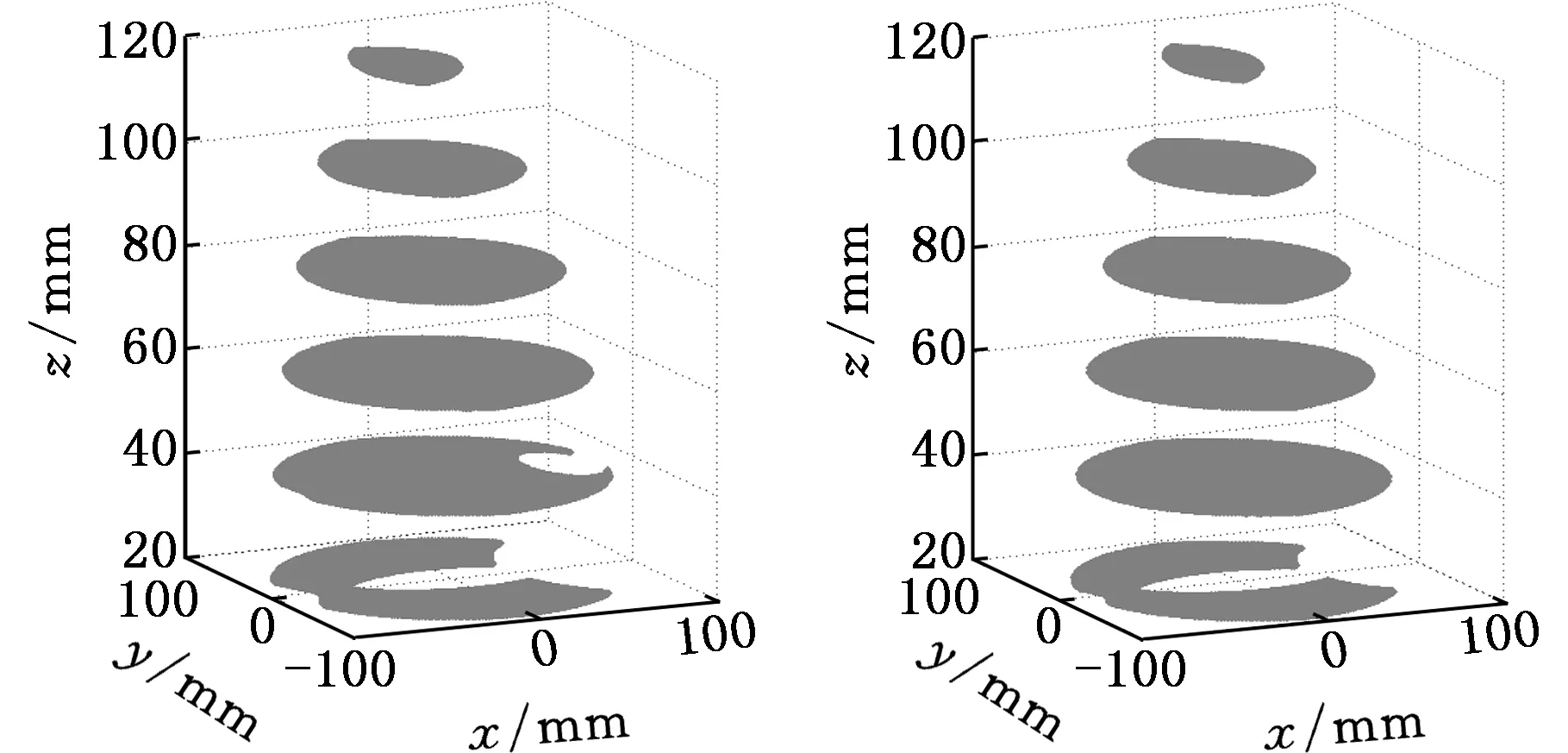
(e)α=120° (f)α=150°图4 工作空间Fig.4 Workspace

3.3 奇异性分析

并联机构的奇异位形可通过上述雅可比矩阵进行分析，主要有逆解奇异、正解奇异和混合奇异三种类型。

3.3.1逆解奇异

逆解奇异发生条件为|Jq|=0，且|Jp|≠0。根据式(16)可知，若Jq对角线上任一元素为零，则|Jq|=0。

由N11=0，N22=0，N33=0，N44=0，可得

(18)

当输入参数满足上述任一方程时，|Jq|=0，机构发生逆解奇异。通常，这类奇异一般发生在机构到达工作空间边界位置或存在多组逆解时。如当杆AiBi和杆BiCi处于拉直共线或重叠共线时，表示机构到达极限位置。

3.3.2正解奇异

正解奇异发生条件为|Jp|=0，且|Jq|≠0。由式(17)可知，若M24=0且M44=0，则|Jq|=0。

由M24=0，M44=0可得

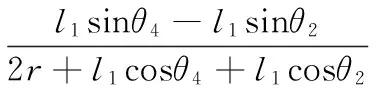
(19)

将求解出的α代入方程M24=0、M44=0，可得出机构正解奇异的位置。当从动杆BiCi与动平台平行或共面时，尽管驱动杆AiBi固定，动平台依然具有运动自由度，机构运动不确定。

3.3.3混合奇异

当|Jq|=0且|Jp|=0时，机构发生混合奇异，此时机构将失去自由度。

4 冗余驱动

为了避免或减轻机构奇异对机构运动性能的影响，可通过增加冗余驱动以消除全部或部分奇异位形。机构奇异的本质是表示机构输入输出关系的雅可比矩阵降秩[10]，机构末端执行器的输出自由度发生变化。若增加冗余驱动后，能够分别使雅可比矩阵在原机构的奇异位置不降秩，即可解决机构的奇异问题。根据机构特点，本文设计两种冗余驱动方式。

4.1 SPS冗余支链

在静平台中心O点和动平台上v轴以外任意位置之间添加SPS支链，P副为驱动，结构原理及三维模型如图5所示。

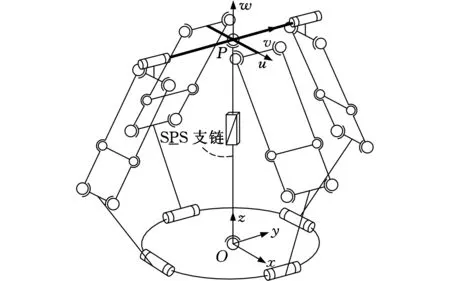
(a)结构原理

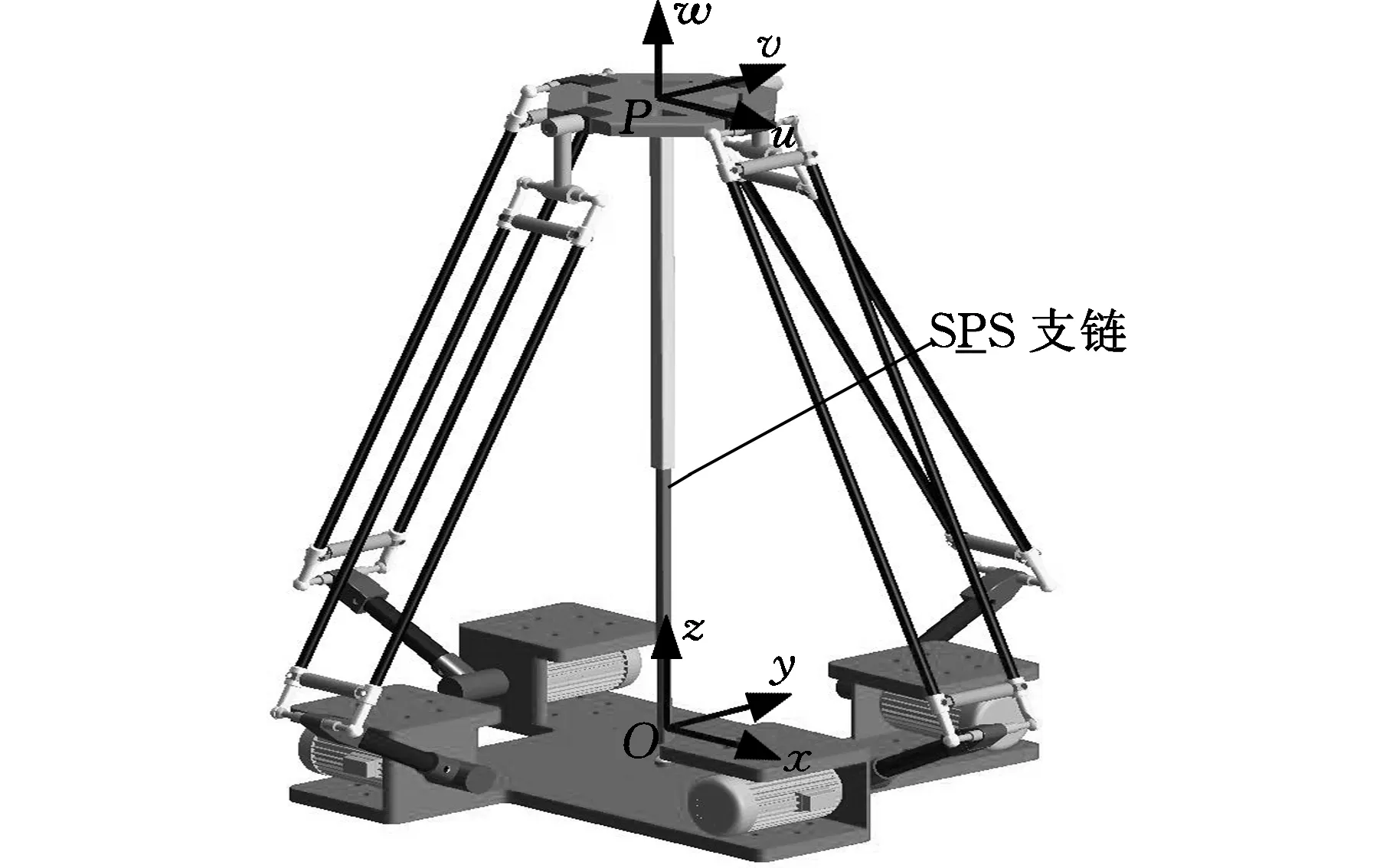
(b)三维模型图5 SPS冗余驱动支链Fig.5 SPS additional active limb

增加冗余驱动后，机构的雅可比矩阵为

(20)

(21)

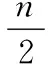
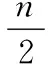
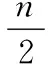
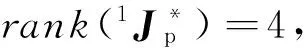
由于移动副固有的结构特性，尽管该冗余驱动方式会提高机构的刚度和承载能力，但其工作空间会大大减少。同时，驱动副位于支链中间，影响了机构的运动性能和灵活性。

4.2 RRR冗余支链

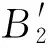
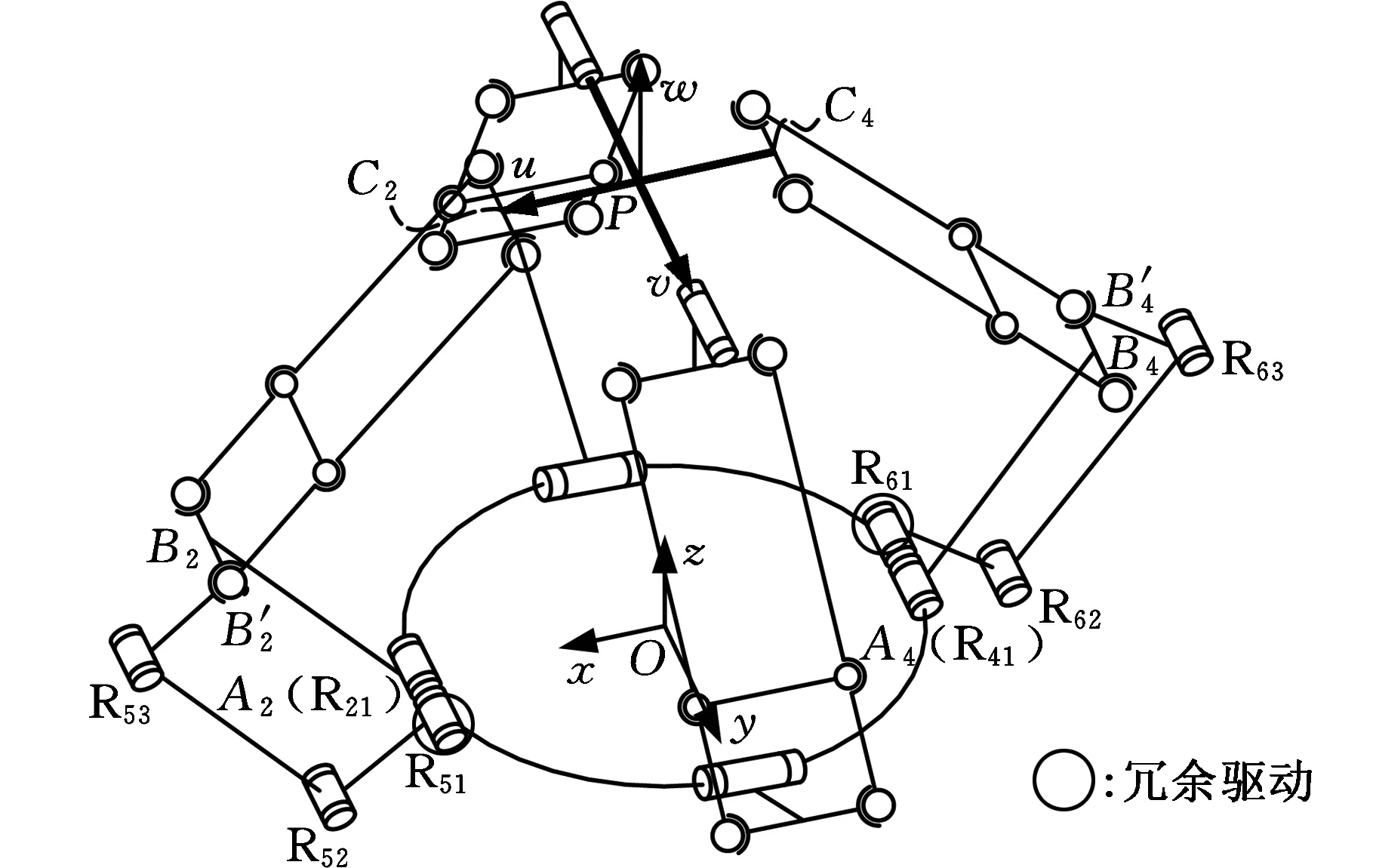
(a)结构原理

(b)三维模型图6 RRR冗余驱动支链Fig.6 RRR additional active limb

机构增加冗余驱动后，雅可比矩阵为

(22)

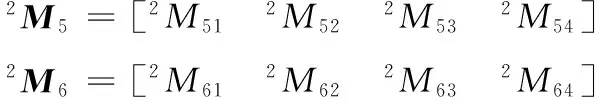
(23)

2M51=-sinθ52M52=02M53=-cosθ5

2M54=nsinαsinθ5+ncosαcosθ5
2M61=sinθ62M62=02M63=-cosθ6

2M64=nsinαsinθ6-ncosαcosθ6

2N52=l1sinθ2sinθ5-l1cosθ2cosθ5

2N55=-(r+l1cosθ2-xP-ncosα)cosθ5-
(zP-nsinα-l1sinθ2)sinθ5

2N64=l1sinθ4sinθ6-l1cosθ4cosθ6

2N66=-(xP-ncosα+r+l1cosθ4)cosθ6-
(zP+nsinα-l1sinθ4)sinθ6

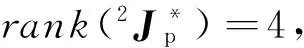
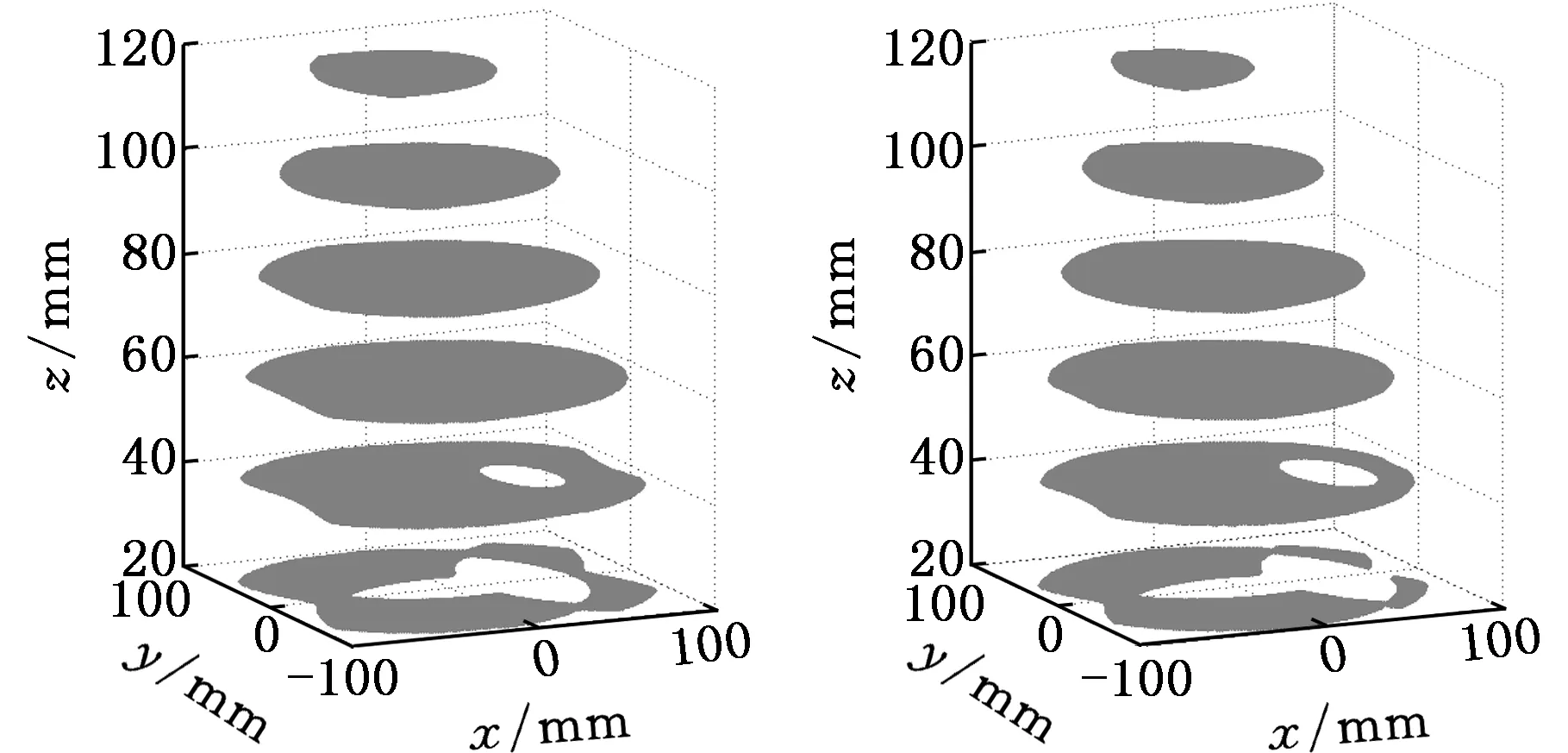
当动平台姿态角为180°时，原机构的工作空间如图7a所示，图中深色部分为空间内部的奇异位置。增加RRR冗余支链后，机构定姿态工作空间如图7b所示，工作空间增大，且内部奇异得到消除，机构的运动性能更好，且这类支链的驱动源可固定安装在定平台上，有利于机构提高运动速度和加速度性能。

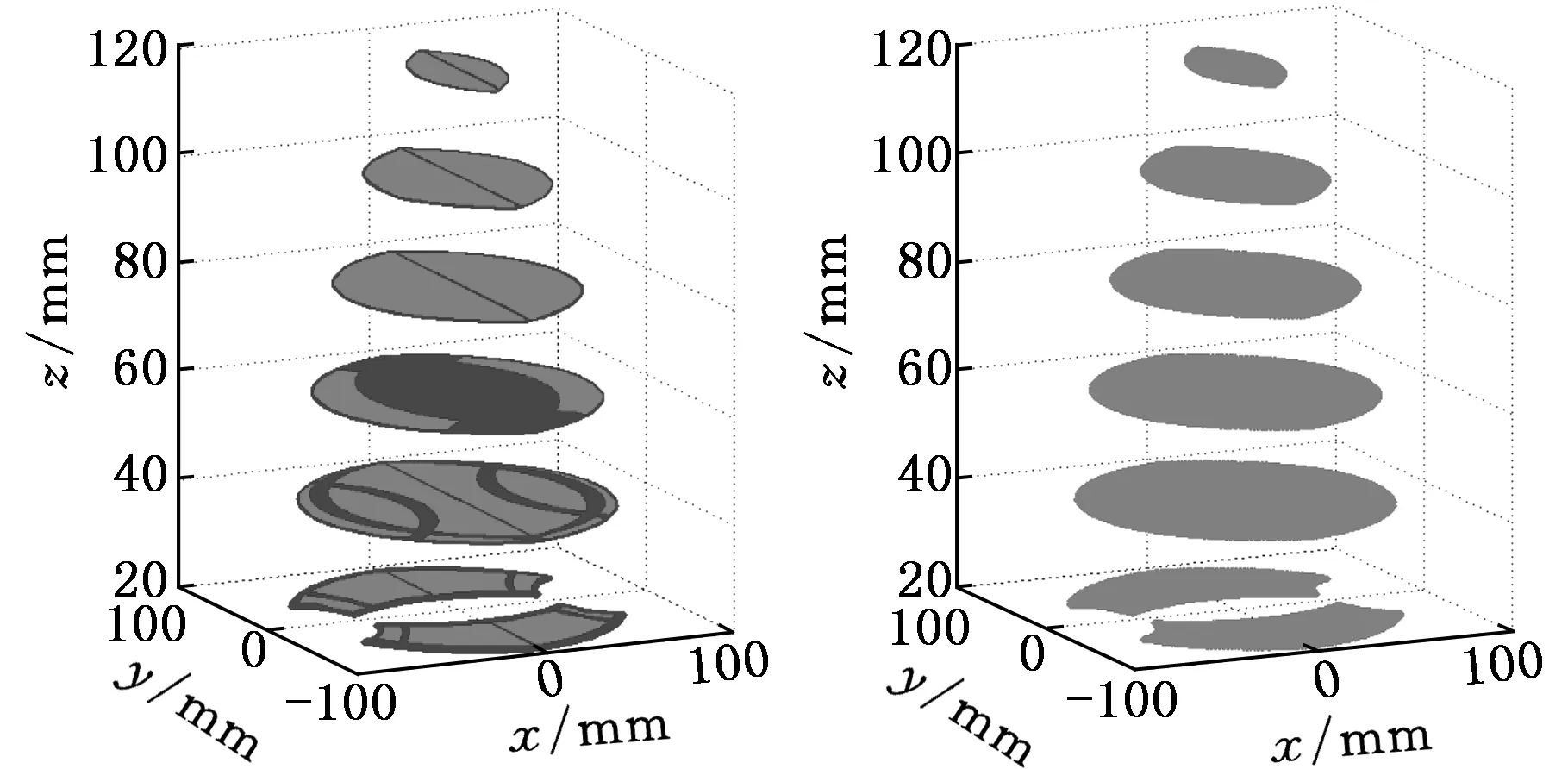
(a)原机构 (b)增加冗余驱动后图7 冗余驱动工作空间Fig.7 Workspace after redundant driving

5 结论

(1)设计一种新型3T1Ry运动并联机构，分析了机构的拓扑结构特性，该机构耦合度为2，耦合性较强，整体结构部分对称。

(2)采用序单开链法建立了机构的正解方程，并通过数值解验证了正反解方程的正确性。

(3)分析了机构的工作空间和奇异位形等运动性能，表明机构具有较大的工作空间，但存在的奇异位置导致工作空间内部不连续。

(4)为了减少机构的奇异位形，设计了两种冗余驱动方式。经分析表明，RRR冗余支链可在不影响机构工作空间的前提下有效消除部分奇异位形，且其驱动源安装在定平台上，便于机构在高速和高加速度场合推广应用。

[1] CLAVEL R. Delta a Fast Robot with Parallel Geometry[C]//Proceedings of 18th International Symposium on Industrial Robots. Lausanne: IFS Publications,1988:91-100.

[2] PIERROT F, COMPANY O. H4: a New Family of 4-DOF Parallel Robots[C]//Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Atlanta: IEEE,1999:508-513.

[3] KRUT S, COMPANY O, BENOIT M, et al. I4: a New Parallel Mechanism for SCARA Motions[C]// Proceedings of the IEEE International Conference on Robotics and Automation. IEEE,2003:1875-1880.

[4] NABAT V, COMPANY O, KRUT S, et al. Par4: Very High Speed Parallel Robot for Pick-and-place[C]// Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. New York: IEEE,2005:1202-1207.

[5] KRUT S, COMPANY O, NABAT V, et al. Heli4: a Parallel Robot for SCARA Motions with a Very Compact Traveling Plate and a Symmetrical Design[C]// Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing: IEEE,2006:1656-1661.

[6] KIM S M，KIM W K，YI B J. Kinematic Analysis and Optimal Design of a 3T1R Type Parallel Mechanism[C]//Proceedings of the IEEE International Conference on Robotics and Automation. Kobe,2009:2199-2204.

[7] KIM S M，KIM W K，YI B J. Kinematic Analysis and Design of a New 3T1R 4-DOF Parallel Mechanism with Rotational Pitch Motion[C]//Proceedings of the IEEE International Conference on Intelligent Robots and Systems. St Louis,2009:5167-5172.

[8] 汪满新，黄田，王立，等. 一种三平一转四自由度并联机构：中国，201510786414.6[P].2015-11-16.

WANG Manxin，HUANG Tian，WANG Li，et al. Four Degree of Freedom Parallel Mechanism with Three Translations and Two Rotations: China，201510786414.6[P].2015-11-16.

[9] 刘辛军，谢富贵，王立平,等. 一种可实现SCARA运动的四自由度单动平台并联机构：中国，201210435375.1[P].2012-11-02.

LIU Xinjun, XIE Fugui, WANG LIping, et al. A 4-DOF Single Motion Platform Parallel Mechanism for SCARA Motions：China，201210435375.1[P].2012-11-02.

[10] 白志富，韩先国，陈五一．冗余驱动消除并联机构奇异研究[J]．航空学报，2006,27(4):733-736.

BAI Zhifu，HAN Xianguo，CHEN Wuyi. Study on Elimination Singularities of Parallel Mechanism by Actuation Redundancy[J]. Acta Aeronauticaet Astronautica Sinica，2006，27(4)：733-736.

[11] 杨廷力，刘安心，罗玉峰，等．机器人机构拓扑结构设计[M]．北京: 科学出版社，2012.

YANG Tingli, LIU Anxin, LUO Yufeng, et al. Theory and Application of Robot Mechanism Topology [M]．Beijing: Science Press,2012.

[12] 冯志友，张策，杨廷力．基于序单开链法的空间4自由度并联机构位置正解[J] . 机械工程学报，2006，42(7)：35-38．

FENG Zhiyou，ZHANG Ce，YANG Tingli．Positional Solution of 4 Degree of Freedom Parallel Mechanism Based on the Ordered SOCS Method Space[J]. Chinese Journal of Mechanical Engineering,2006,42(7):35-38.