单自由度复杂平面连杆机构的奇异性分析

王 君 牛克佳 聂良益 何红秀 陈智龙 汪 泉 任 军

1.湖北工业大学机械工程学院,武汉,4300682.中国地质大学机械与电子信息学院，武汉，430074

0 引言

平面连杆机构的奇异位置(死点)也是连杆机构可动性问题的主要研究方面之一。目前，已有不少学者提出了不同的解决办法。江国宪等[1]采用等效机械手工作空间分析了平面四杆机构的可动性问题。宋杰等[2]采用虚杆等效方法研究了RRP-RRP型六连杆机构的曲柄存在条件。于红英等[3]运用平面铰链五连杆机构的雅可比矩阵求出了机构奇异位置。王文格等[4]采用机构的雅可比矩阵研究了七杆机构的可动性特点。沈惠平等[5]提出了任意复杂多回路平面连杆机构或机械手奇异位形分析的模块法。GOSSELIN等[6]基于雅可比矩阵的特性将闭链机构的奇异性分为三种类型。WANG等[7]用判别式法研究了Stephenson六杆机构的奇异性。 GAO等[8]分析了对称五杆机构在解空间的奇异位形。MERLET[9]采用线汇与线丛原理对奇异位形进行了研究。COLLINS等[10]应用Clifford 代数研究了并联操作平台的奇异性问题。WANG等[11]采用机构自由度退化方法分析了一系列复杂平面机构的死点位置。TING等[12]对一些复杂机构的曲柄存在条件做了初步讨论。这些方法大多针对特定机构，且基本上是采用几何分析与代数计算的方法。

本文利用连杆机构本身的特性，采用等效四杆机构的概念来分析单自由度复杂连杆机构的奇异性问题。

1 等效四连杆机构

1.1 等效四连杆机构概念提出

HAIN[13]首先使用一阶等效机构的概念分析多杆机构的速率问题。DIJKSMAN[14]提出了一种能保持一阶等效运动特性的连杆机构简化方法。一阶等效连杆机构是由构件的瞬心组成，并保持与原机构中连杆之间瞬时运动特征不变的机构。其中，这些瞬心可以看作是原始连杆机构中相邻两构件的瞬时运动关节。由此，等效连杆机构的杆件数量比实际机构的杆件数量少，这就提供了另一种方法来研究机构的运动状态。对于单自由度复杂平面连杆机构，其一阶运动特性可以用它的等效四杆机构来体现。等效四杆机构是由原连杆机构中4个原始连杆之间两两相邻连杆间的4个速度瞬心构成的，其中一个瞬心可以作为输入关节。因为瞬心既能用来判断给定连杆的速度分布，又可以判断连杆间的运动传递特性，所以等效四杆机构可以代表单自由度复杂平面连杆的一阶运动特性。

从原始的复杂连杆机构中找到4个连杆或相应的4个速度瞬心来组成等效四杆机构成为研究的重点。等效四杆机构包含一个输入关节，这个输入关节连接着复杂连杆机构中的两个连杆，这两杆可以看作是机架杆和输入杆；还需要另外的两杆来构成等效四杆机构的四杆，这两杆可以看作是连架杆和输出杆，输出杆和连架杆可以是原复杂连杆机构中的任意两杆。把这4个杆件按照机架、输入杆、连架杆、输出杆的顺序组合，这些杆件两两相邻的瞬心就构成了等效四杆机构的4个瞬时关节。这样的等效四杆机构可保持复杂平面连杆机构中原始连杆之间的瞬时运动特性。

1.2 等效四连杆机构的构成

由上述分析可知，等效四连杆机构由4个原始杆以及它们对应的4个运动瞬心组成。4个原始杆中，连接机架和输入杆组成输入关节，另外两杆为原复杂连杆机构中的任意两个杆件。如图1所示，找出Stephenson六杆机构的瞬心，则其瞬时运动特性可以由A0ECC0组成的等效四杆机构来决定。

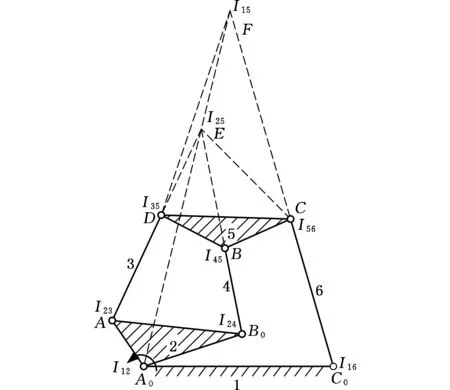
图1 Stephenson Ⅱ型六杆机构Fig.1 Stephenson type Ⅱ six-bar linkage

复杂机构的等效四连杆机构可以按照以下步骤找出：①选择机架和输入杆，其所相连的关节即为输入关节；②任选两杆为其余两杆；③按照机架、输入杆、连架杆、输出杆的顺序组合构成等效机构的原始四杆，并找出相邻两杆之间对应的瞬心。这4个相邻的瞬心就构成了等效四杆机构的4个关节，相邻两个关节之间的杆或等效杆就成为等效机构的4个杆件。

需要注意的是，如果复杂平面连杆机构含有一个四杆环，且该四杆环包括了机架与输入杆，则该四杆环可作为该复杂机构的一种等效四杆机构。由此，复杂连杆机构的等效四杆机构可分成如下两种类型。

类型Ⅰ 等效四杆机构的4个杆件由原复杂连杆机构内的四杆环组成。

类型Ⅱ 等效四杆机构的4个杆件由原复杂连杆机构内的非四杆环组成。

类型Ⅰ的复杂连杆机构的等效四连杆机构直接为该机构内的四杆环。对于类型Ⅱ中的等效四连杆机构，其构成的杆件可能来自四杆环的一部分但不能是全部，或来自其他不同环。因复杂连杆机构中存在多个杆件，因此有多个等效四连杆机构的杆件组合方式。这些等效四杆机构都从属于类型Ⅰ或类型Ⅱ。图1等效四连杆机构A0ECC0中，连杆EC和复杂连杆机构中的三元杆BCD具有相同的运动状态。当杆1作为机架，杆2作为输入杆，或瞬心I12作为输入关节时，杆A0E和杆A0AB0可等效成同一个单元。该六连杆机构能被等效为四连杆机构A0ECC0。需要注意的是，点E为杆AD、B0B延长线的交点，同时也是瞬心I25。由此，等效四连杆机构A0ECC0可以看作是由原始四杆1、2、5和6按顺序排列的两两相邻的4个关节瞬心I12、I25、I56和I61组成的，即等效四杆机构的4个关节就是原四杆中相邻两杆之间的瞬心，它是类型Ⅱ等效四连杆机构。

选择其他杆件组合也能构成等效四杆机构。如选择杆件1作为机架，杆件2为输入杆，杆件3和杆件5为剩余两杆，并按顺序排列的四杆件1、2、3和5形成的瞬心I12、I23、I35和I51就构成了等效四连杆机构A0ADF。其余的等效四连杆机构也可以用相同的方法得到。

2 运用等效四连杆机构分析机构的死点

平面四杆机构出现运动死点的位置是在连杆和输出杆共线或三个非输入关节共线的位置。因复杂平面连杆机构具有更多的杆件、更复杂的环和更多样的输入方式，故很难分析其出现死点的位置与机构在死点位置的构型。等效四连杆机构概念的提出为研究单自由度复杂平面连杆机构的死点位置提供了一种新方法。

等效四杆机构包含一个输入关节和三个非输入关节。如果复杂连杆机构对应的等效四连杆机构处在死点位置，则原复杂平面连杆机构也必处在死点位置。由此，单自由度复杂平面连杆机构的死点可以按照以下判别准则来分析。

判别准则1 单自由度复杂平面机构死点出现的条件是该机构的等效四连杆机构中的三个非输入关节处在同一直线上。

判别准则2 任一个该复杂机构的等效四连杆机构处在死点位置，则整个原机构一定也处于死点位置。

需要说明的是，如果类型Ⅰ等效四连杆机构处在死点位置，那么原复杂机构也必处于死点位置，并且所有类型Ⅱ等效四连杆机构也处于死点位置。如果任一该机构类型Ⅱ等效四连杆机构处于死点位置，该复杂机构也处于死点位置，其余所有类型Ⅱ等效四杆机构也都处于死点位置，但此时该复杂机构的类型Ⅰ等效四连杆机构不一定处于死点位置。也就是说，该复杂连杆处于死点位置时，该机构的任一个类型Ⅱ的等效四杆机构机构都处于死点位置。这是因为类型Ⅱ的等效四连杆机构中的杆件是来自该复杂机构中不同的环。当所有类型Ⅰ和类型Ⅱ等效四杆机构都处于死点位置时，则原机构必处于死点位置。

下面对以上准则进行进一步解释。如图2所示，以杆件1作为机架，杆件2为输入杆，杆件p和杆件q是该复杂机构中不同于杆件1、杆件2的其余任意两杆。该等效四杆机构对应的瞬心为I12、I2p、Ipq和I1q。

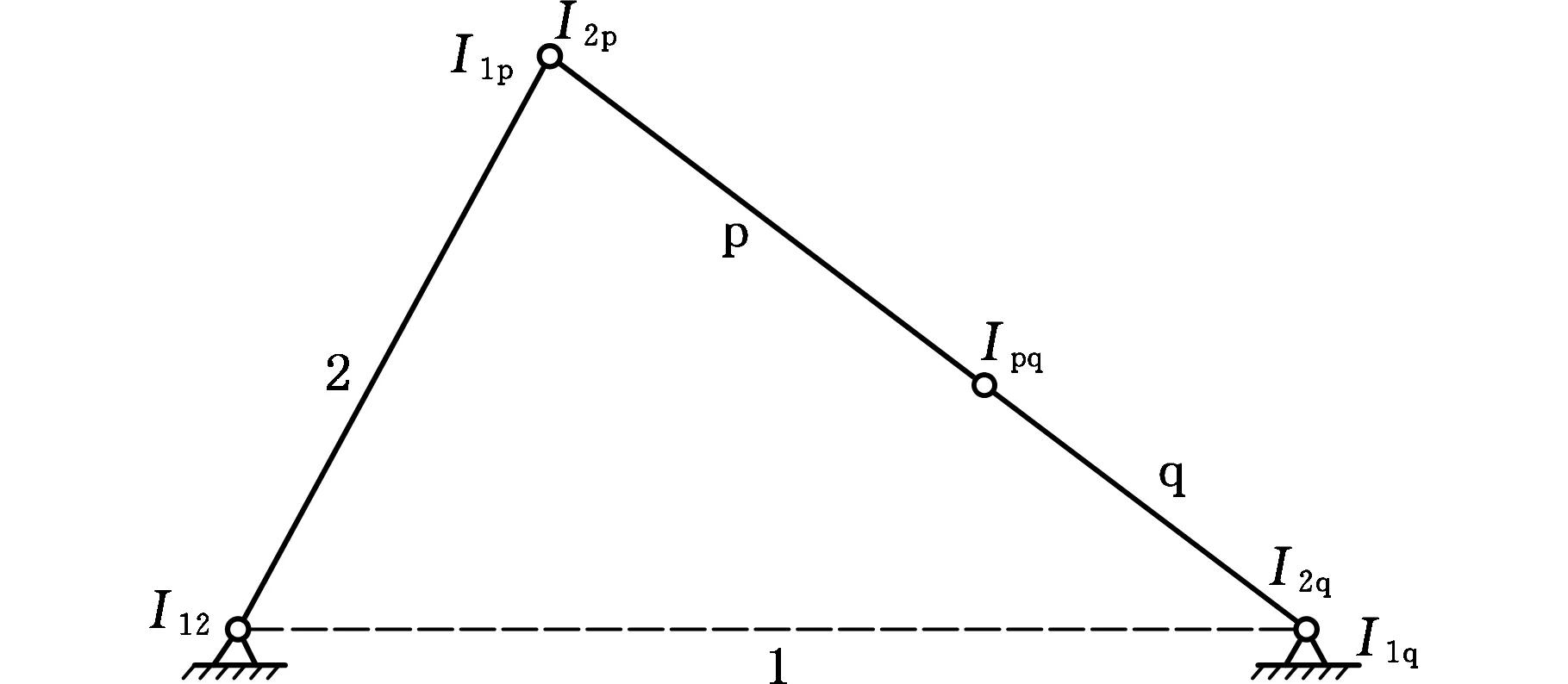
图2 四连杆机构Fig.2 A four-bar linkage

杆件p、杆件q以及杆件2的速度关系可以表示为

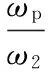
(1)

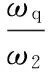
(2)

式中,ωi(i=2,p,q)为杆件i的角速度。

当复杂连杆机构处于死点位置时，式(1)和式(2)的值应该是无穷大的，此时等式的右半部分的分母应等于0，即I1pI2p=0和I1qI2q=0，这时瞬心I1j和I2j(j=p,q)重合。根据Aronhold-Kennedy理论，瞬心Ipq在直线I1pI1q和直线I2pI2q上。由此，等效四连杆机构中的三个非输入关节I2p、Ipq和I1q处在同一直线上。如果等效四连杆机构中的三个非输入关节I2p、Ipq和I1q处在同一直线上，同理，根据Aronhold-Kennedy理论，瞬心I1j和I2j(j=p,q)必重合。当杆件p和杆件q被任意地选取时，一个类型Ⅱ的等效四连杆机构处于死点位置，其余所有类型Ⅱ的等效四连杆机构一定同时处于死点位置。由此，该判别准则是单自由度复杂平面连杆机构死点位置的充分必要条件，这些准则能简单判别单自由度复杂平面连杆机构死点的几何构型。

3 实例分析

3.1 含有两个移动关节的平面六连杆机构死点位置分析

如图3所示,Stephenson六连杆机构中的2个转动关节用移动关节代替时，其死点问题也能利用等效四连杆机构的方法来判定。当给定输入在关节A时，如选择构件3和构件4为其余两杆，运用等效机构的概念和方法，机构的死点位置出现在类型Ⅰ等效四杆机构I12I24I34I13中的瞬心I24、I34和I13共线(图3a)。同时四杆环ABCD在物理上形成一个曲柄滑块机构，即类型Ⅰ的等效四杆机构，根据上述准则1和2，此时四杆环ABCD一定处在死点位置,BC杆垂直于滑块的导路方向。若选择杆4和杆5为其余的两杆，运用三心定理容易得到杆2和杆5的运动瞬心I25、杆1和杆5的运动瞬心I15，机构的奇异位置出现在类型Ⅱ等效四杆I12I25I45I15中的瞬心I25、I45和I15共线(图3b)，此时杆件EF将垂直于平面内滑块所运动的导路方向。

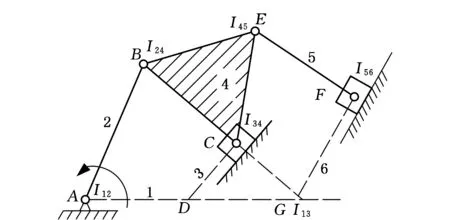
(a)

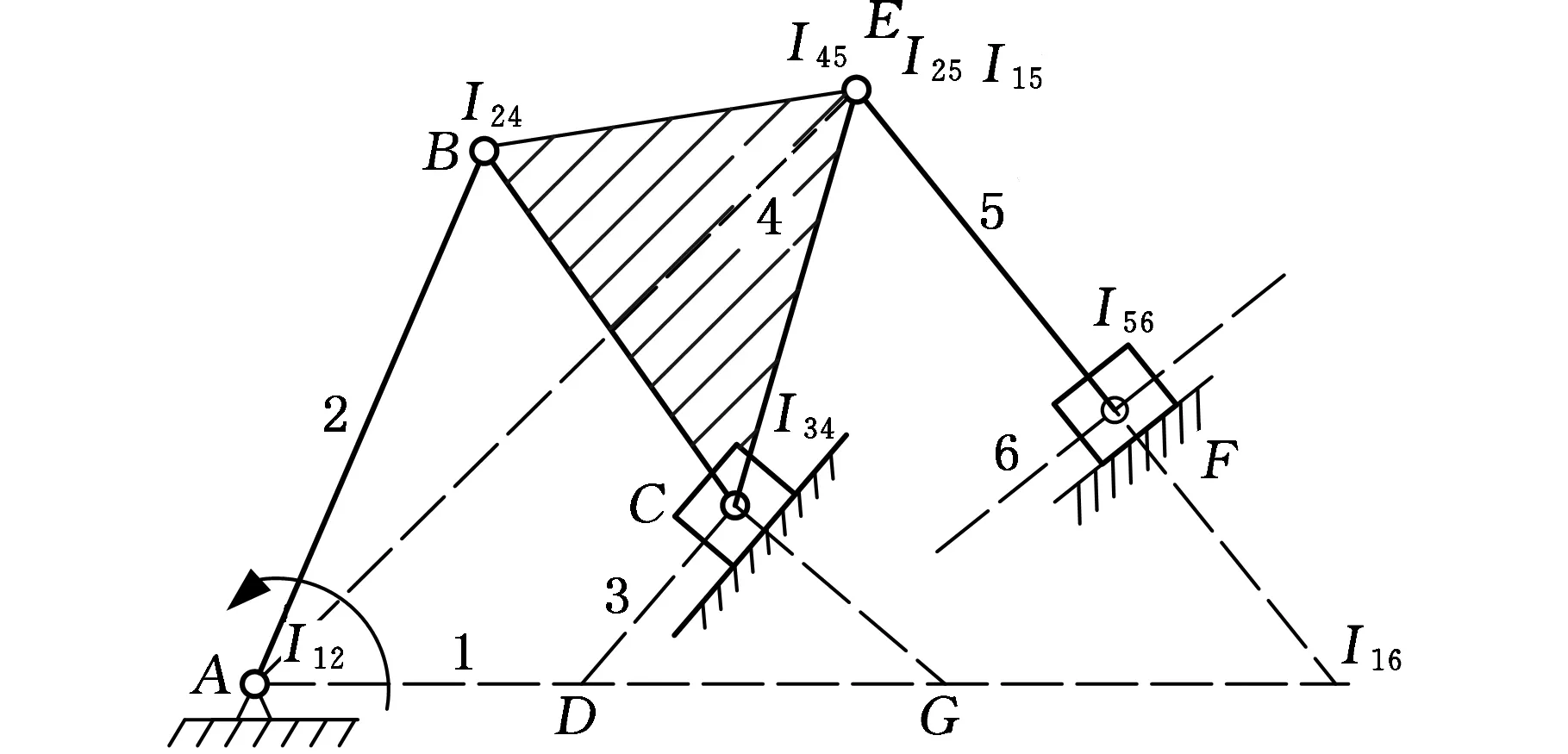
(b)图3 含有两个移动关节的六杆机构Fig.3 A six-bar linkage with two sliders

3.2 含有三个移动关节的六杆机构的死点位置

将六杆机构中三个旋转关节用移动关节替换，如图4所示。若以旋转关节A为输入关节，则默认杆1为机架，杆2为输入杆，任选杆3和杆4为其他两杆，机构的奇异位置出现在等效四杆I12I24I34I13中的瞬心I24、I34和I13共线，或任选杆4和杆5为任意两杆，机构的奇异位置出现在等效四杆I12I25I45I15中的瞬心I25、I45和I15共线。

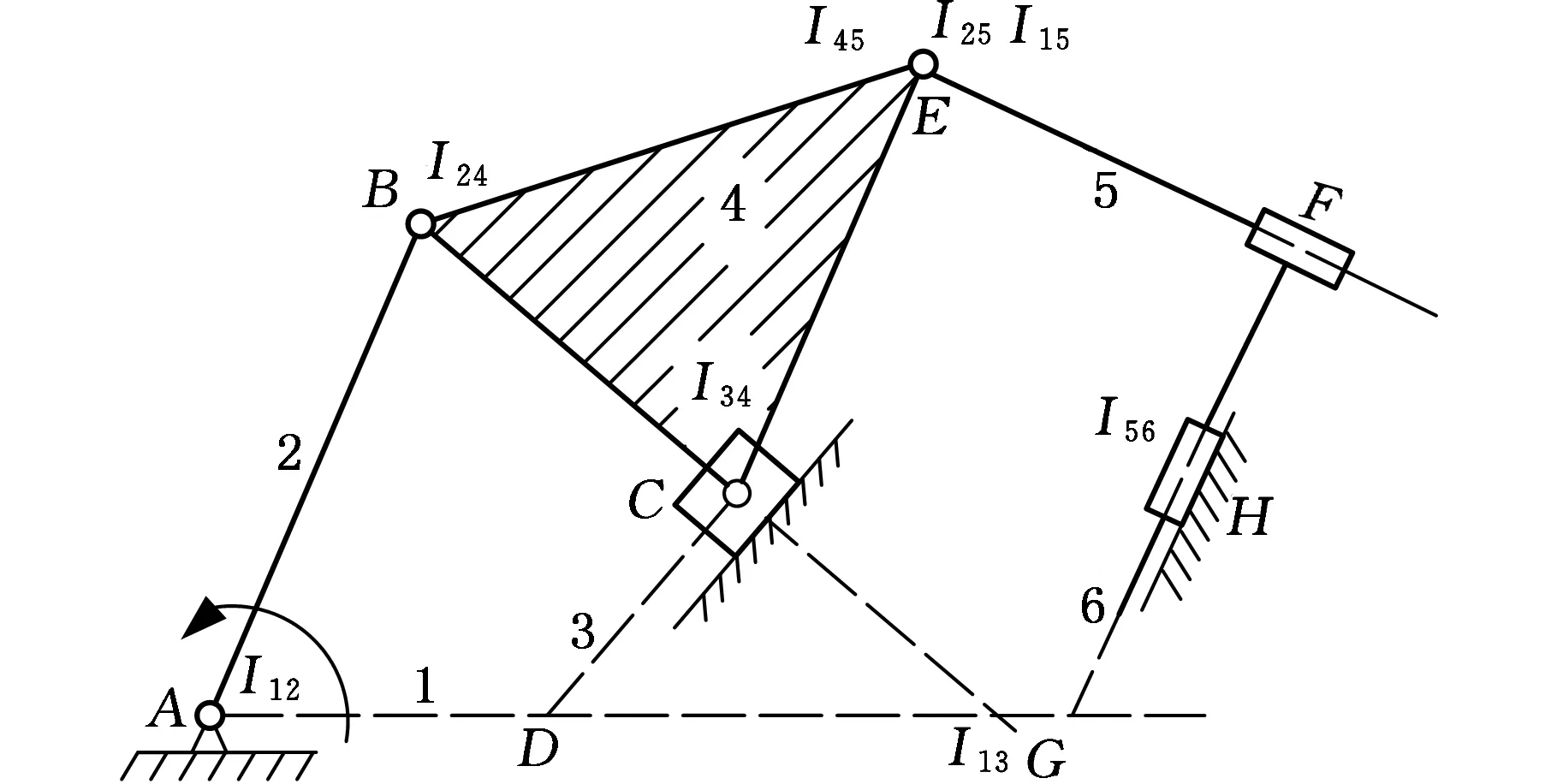
图4 含有三个移动关节的六杆机构Fig.4 A six-bar linkage with three sliders

3.3 单自由度双蝶八连杆机构死点位置分析

单自由度双蝶八杆机构的死点位置是很难找出来的。这里将运用PENNOCK等[15]提出的方法求得单自由度双蝶八杆机构所有的瞬心。利用本文提出的等效机构方法，复杂的单自由度双蝶八杆机构的奇异性很容易就被分析出来,通过任一等效机构可以得到其死点位置。如图5所示，任意选择原机构的4根杆如杆1、2、3和7，并把它们按照机架、输入杆、连杆、输出杆的顺序组合。由相邻两杆之间的运动瞬心组成相应的等效四杆机构I12I23I37I17。如果该等效机构的三个被动关节I23、I37、I17位于同一直线上，则这个等效四杆机构位于死点位置，进而判定整个单自由度双蝶八杆机构必定位于死点位置。如选择其他任意连杆及输出杆，也会得出相同的结论。由此，运用等效四杆机构的概念，像单自由度双蝶八杆机构的死点位置也可很容易地判别出来。

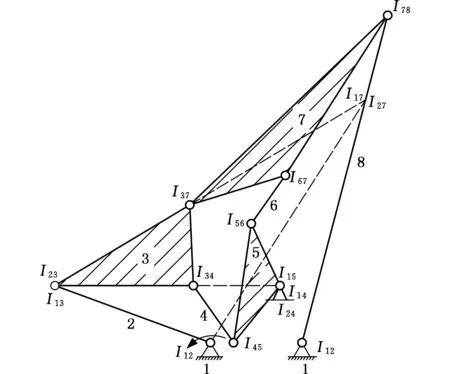
图5 单自由度双蝶八杆机构的死点位置Fig.5 A dead center position for the double butterfly eight-bar linkage

4 结束语

本文根据机构的瞬心能表示该机构的运动特性的特点，提出了用等效四连杆机构的概念和方法来研究单自由度复杂平面连杆机构奇异性的方法。以Stephenson六连杆机构为例介绍了等效四连杆机构构成，并利用其来分析更复杂的单自由度平面连杆机构如带移动关节的六连杆机构、双蝶八杆机构的奇异性，体现了该方法的简单直观性。该方法是一种几何分析方法，能为研究复杂平面机构在奇异位置的构型提供一种新的思路。

[1] 江国宪，朱本富. 用等效机械手工作空间的方法分析平面四杆机构的可动性[J].吉林工业大学学报，1990, 20(2):67-75.

JIANG Guoxian, ZHU Benfu. Analysis of t-he Movability of Planar Four-bar Mechanismby Equivalent Manipulator Working Space[J].Journal of Jilin University of Technology,1990, 20(2):67-75.

[2] 宋杰，梅瑛，李瑞琴. 平面3-DOF PRR-RRP型六杆机构的曲柄存在条件[J].机械传动，2013,37(11):32-34.

SONG Jie, MEI Ying, LI Ruiqin. Crank Existence Condition of Planar 3-DOF PRR-RRP Type Six-bar Mechanism[J]. Journal of Mechanical Transmission,2013,37(11):32-34,170.

[3] 于红英，唐德威. 平面铰链五杆机构的奇异性研究[J].哈尔滨工业大学学报, 2007,39(3):381-385.

YU Hongying, TANG Dewei. Study on the Singularity of a Planar Five-bar Mechanism [J]. Journal of Harbin Institute of Technology,2007,39(3):381-385.

[4] 王文格, 张文彬. 双伺服驱动七杆机构研究[J]. 机械传动, 2014,38(11):10-13.

WANG Wenge, ZHANG Wenbin. Research of a Seven-bar Mechanism with Double Servo Drive[J]. Journal of Mechanical Transmission,2014,38(11):10-13.

[5] 沈惠平，杨廷力. 三个复杂基本运动链奇异性条件的求解与识别[J]. 机械科学与技术，2000,19(5):750-752.

SHEN Huiping, YANG Tingli. Solutions for Singularity Conditions for Three Complex Basic Kinematic Chain[J]. Mechanical Scienceand Technology,2000,19(5):750-752.

[6] GOSSELIN C, ANGELES J. Singularity Analysis of Closed-loop Kinematic Chains [J]. IEEE Transactions on Robotics & Automation,1990,6(3):281-290.

[7] WANG J, TING K L, XUE C. Discriminant Method for the Mobility Identification of Single Degree-of-freedom Double-loop Linkages[J]. Mechanism & Machine Theory,2010,45(5):740-755.

[8] GAO F, ZHANG X Q, ZHAO Y S, et al. Distribution of Some Properties Physical Model of the Solution Space of 2-DOF Parallel Planar Manipulators [J]. Mechanism & Machine Theory,1995,30(6):811-817.

[9] MERLET J P.Singular Configurations of Parallel Manipulators and Grassman Geometry[J]. International Journal of Robotics Research,1989,8(5):45-56.

[10] COLLINS C L, MCCARTHY J M. The Quartic Singularity Surfaces of Planar Platformsin the Clifford Algebra of the Projective Plane[J]. Mechanism & Machine Theory,1998,33(7):931-944.

[11] WANG J, NIE L Y, WANG Q, et al. Singularity Analysis of Planar Multiple-DOF Linkages[C]// ASME 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Buffalo, NY,2014:V05AT08A051.

[12] TING K L, WANG J, XUE C, et al. Full Rotatability and Singularity of Six-bar and Geared Five-bar Linkages[J]. Journal of Mechanisms & Robotics,2010,2(1):298-320.

[13] HAIN K. Applied Kinematics[M]. 2nd ed., New York: McGraw-Hill,1967.

[14] DIJKSMAN E A. Why Joint-joining is Applied on Complex Linkages[C]// Second IFToMM International Symposium on Linkages and Computer Aided Design Methods, SYROM’77.Bucharest, Romania,1977:185-212.

[15] PENNOCK G R, KINZEL E C. Path Curvature of the Single Flier Eight-bar Linkage[J].Journal of Mechanical Design,2004,126(3):217-226.