一种管道机器人的自适应主动螺旋式驱动机理分析

闫宏伟 焦彪彪 马建强 崔子梓 汪 洋

中北大学机械工程学院，太原，030051

0 引言

流体管道作为一种重要的物料输送设施，在流程工业、石油天然气、军事设备、核工业等领域中得到了广泛应用，但是由于重压、腐蚀、制造、人为失误等因素，管道会不可避免地出现裂纹、变形或凹陷等缺陷和泄漏现象[1-2]，在很多工况下，监测和维护需要在人所不能接触的管道内部环境中进行，因此需要管道机器人携带传感器及辅助设备，沿管道行走定期巡查检测，甚至实时修复其存在的缺陷[3-5]。

20世纪50年代国外就已经开展了关于管道机器人的相关研究，随之出现了多种驱动方式的管道机器人系统，以适应不同工况要求[6-7]。机器人的驱动形式主要有：轮式、管道式、履带式、行走式、支撑式、螺旋式、蠕动式和蛇形式等8种驱动方式。20世纪末，相关的管道公司和学者逐渐开始对具有大驱动力、强负载能力的油气管道机器人进行相关应用研究[8-9]。HIROSE等先后成功研制了ThesⅠ、ThesⅡ、ThesⅢ型管道机器人[10]。美国随即研制了Versatrax管道机器人系列[11]。以上研究主要针对管道机器人的图像识别、智能控制等方面[12]。机构运动方式作为管道机器人的核心，决定了机器人在复杂管道中的通过性和对管径变化的整体适应性能。近年来管道机器人驱动结构方面的研究成果较少。国内对管道机器人技术的研究起步较晚，20世纪70年代国内的科研院所相继开始研发管道机器人，如国防科技大学、哈尔滨工业大学、中国科学院沈阳自动化研究所机器人学国家重点实验室、清华大学和北京航空航天大学。所研发的管道机器人种类繁多，应用广阔，部分已经产业化，但大多数是针对特定的几项功能而设计，与国外先进技术均有一定的差距[13-14]。

近几年来，具有特种功能的管道机器人技术的研究在国内外逐渐兴起[15]，其中，螺旋式驱动管道机器人最具代表性。相比常规的管道机器人存在的驱动系统繁琐复杂、机构笨重等缺点，螺旋式驱动系统具有结构简单、运行稳定等优点。然而，通常情况下螺旋式驱动管道机器人的被动驱动方式的传动效率较低、牵引力不足，无法承载检测和修复设备在管道中作业[16]，对管道变形或变径部位的适应能力较差。为此，需要研制一种具有足够大牵引力、结构简单、环境适应性强、运行稳定可靠的新型管道机器人。本文针对螺旋式驱动管道机器人的现有不足，提出了一种利用微型液压系统实现主动驱动的新型螺旋式管道机器人爬行系统。

1 爬行装置结构及驱动机理分析

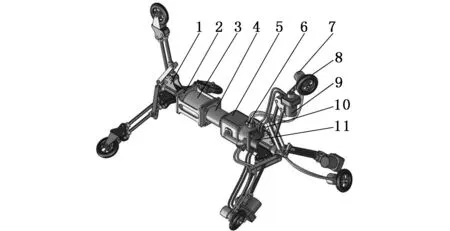
1.连杆支撑骨架 2.电机架 3.电机 4.联轴器 5.齿轮泵 6.限流器 7.液压马达 8.驱动轮 9.转角缸 10.主油路油池 11.转角调节油池图1 变截面管道机器人爬行装置示意图Fig1 The diagram of variable cross-section pipeline crawling device

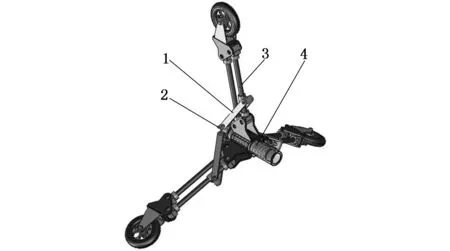
1.中心连杆机构 2.拉杆 3.四连杆机构 4.弹簧图2 三角形连杆支撑骨架原理示意图Fig.2 The supporting schematic diagram of triangle connecting rod frame

变截面管道机器人爬行系统基本构成如图1所示，按功能可分为连杆支撑骨架和集成液压驱动系统两部分。主体骨架结构如图2所示，采用正三角形支撑方式，由四连杆机构、拉杆、中心连杆机构和弹簧共同构成了以机器人轴线为中心的变径支撑机构。中心连杆机构在弹簧的作用下实现滚轮相对中心轴线在径向同步伸缩运动，同时为滚轮和管道内壁的接触滚动提供了所需的预紧力，从而适应爬行装置运动过程中管道内壁截面变化。集成液压驱动系统安装在支撑骨架上，通过双向齿轮泵驱动液压马达和转角缸对驱动轮的转速和倾角实施控制，并使爬行系统具有自适应性。

1.1 变截面运动机理

为满足介质输送要求，常会出现不同内径的管道相互连接的情况，其中变径管和变径弯头是其常见的连接管件。爬行装置在这两种管件中的运动机理对管道机器人的自适应性能非常重要，现分别针对上述两种工况对文中模型进行分析。

1.1.1直行变径运动分析

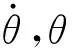
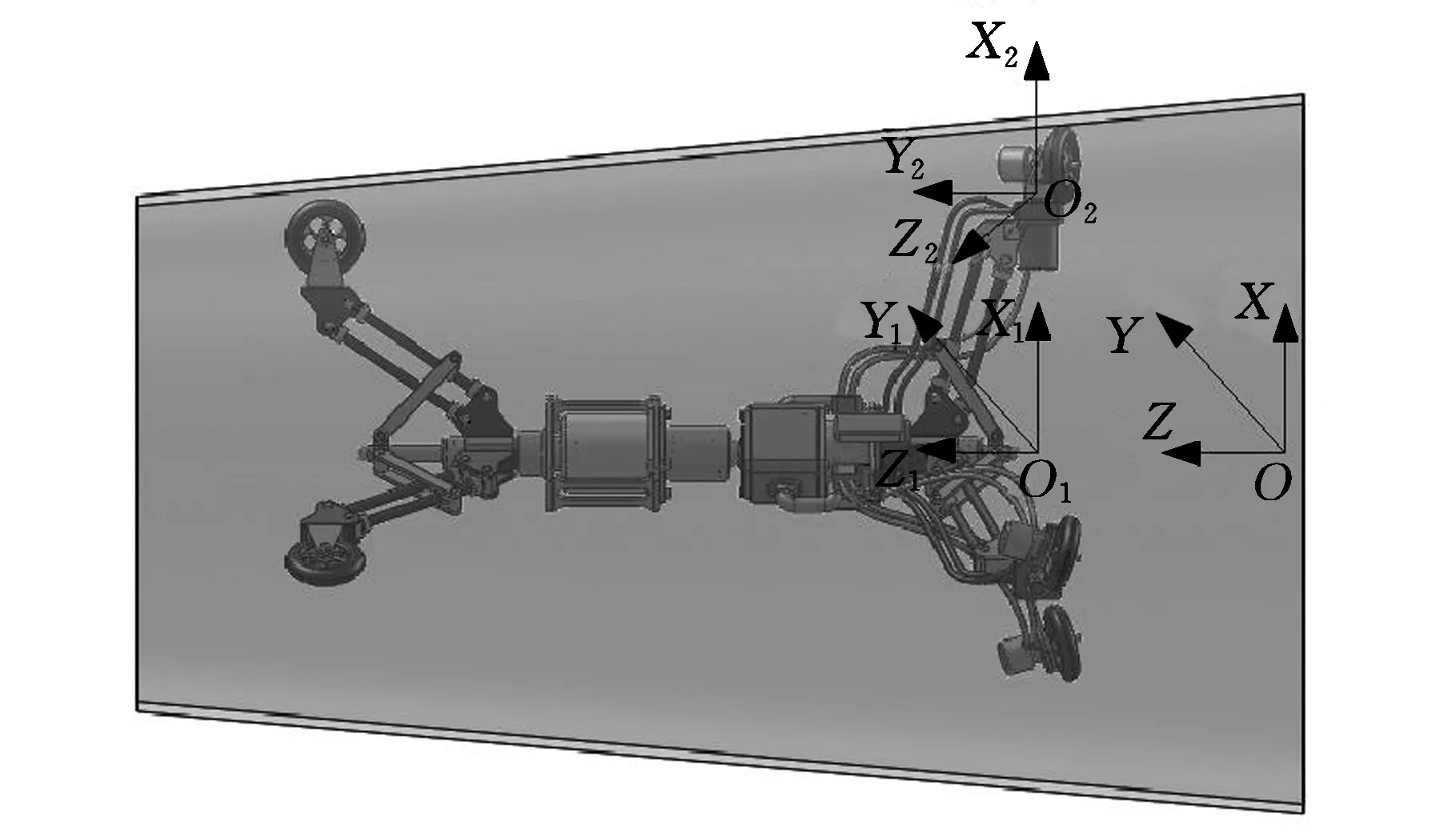
图3 直线变径爬行工况示意图一Fig.3 The first diagram of linear variable diameter crawling conditions

变径管内壁在OXYZ中的几何关系如下：

(1)

式中，r0为在坐标零点处的初始半径；k为变径系数；θd为转角缸转轴轴线与Y轴在XY平面内的夹角。

由上述关系可得到如下齐次变换矩阵：

(2)

(3)

d=r0-kz-rd-a

则由坐标轴转换关系得驱动轮与管壁接触点P在OXYZ中的齐次坐标：

(4)

由式(1)～式(4)可得接触点P在OXYZ中坐标：

(5)

将式(5)两边对时间求导得

(6)

在驱动轮与管道内壁无相对滑动的情况下，接触点P在O2X2Y2Z2中Y2轴方向速度为零，则有

(7)

e=(sinθcosα,cosθcosα,sinα)T

式中，e为O2X2Y2Z2中Y2轴在全局坐标系中的方向向量。

将式(6)代入式(7),得

(8)

对应的转角缸有

(9)

式中，下标i=1,2,3,对应相应驱动部件。

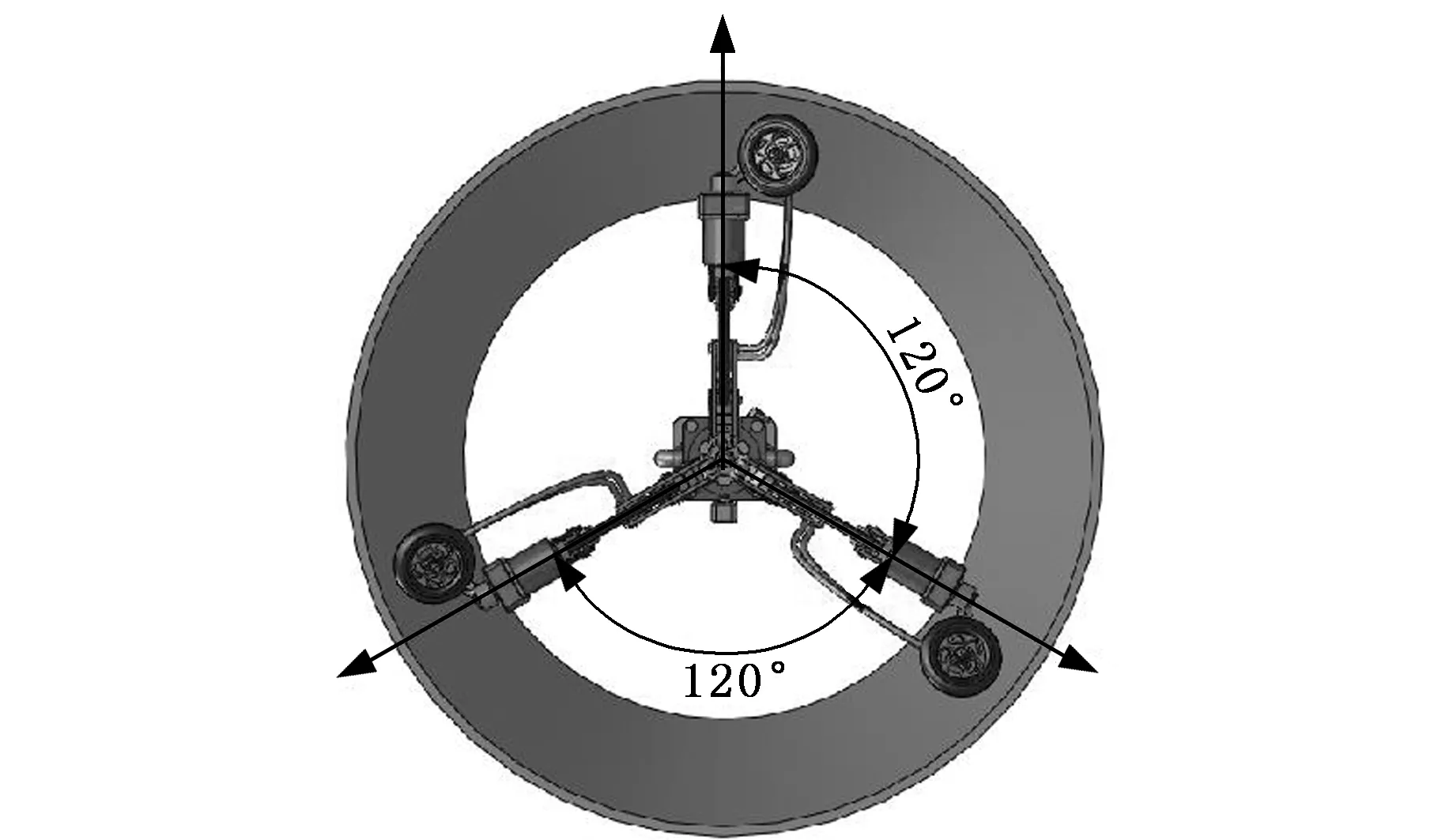
图4 直线变径爬行工况示意图二Fig.4 The second diagram of linear variable diameter crawling conditions

三个驱动轮中心在垂直于爬行装置中心轴的平面内，相对于轴线呈正三角形分布，则对于参数θ有如下关系：

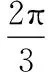
(10)

故

(11)

α1=α2=α3

(12)

(13)

1.1.2变径弯管运动分析

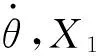
变径弯头内壁在OXYZ中的几何关系如下:

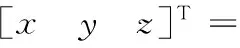
(14)

式中，tran、rot分别表示平移和转动矩阵；R0为弯管中心弧线曲率半径；rw为β=0时弯管内壁与X1Y1面交线圆半径；kw为弯管变径系数；θw为接触点与原点连线与Y1轴在X1Y1平面内的夹角；C为弯管内壁与X1Y1平面交线方程。

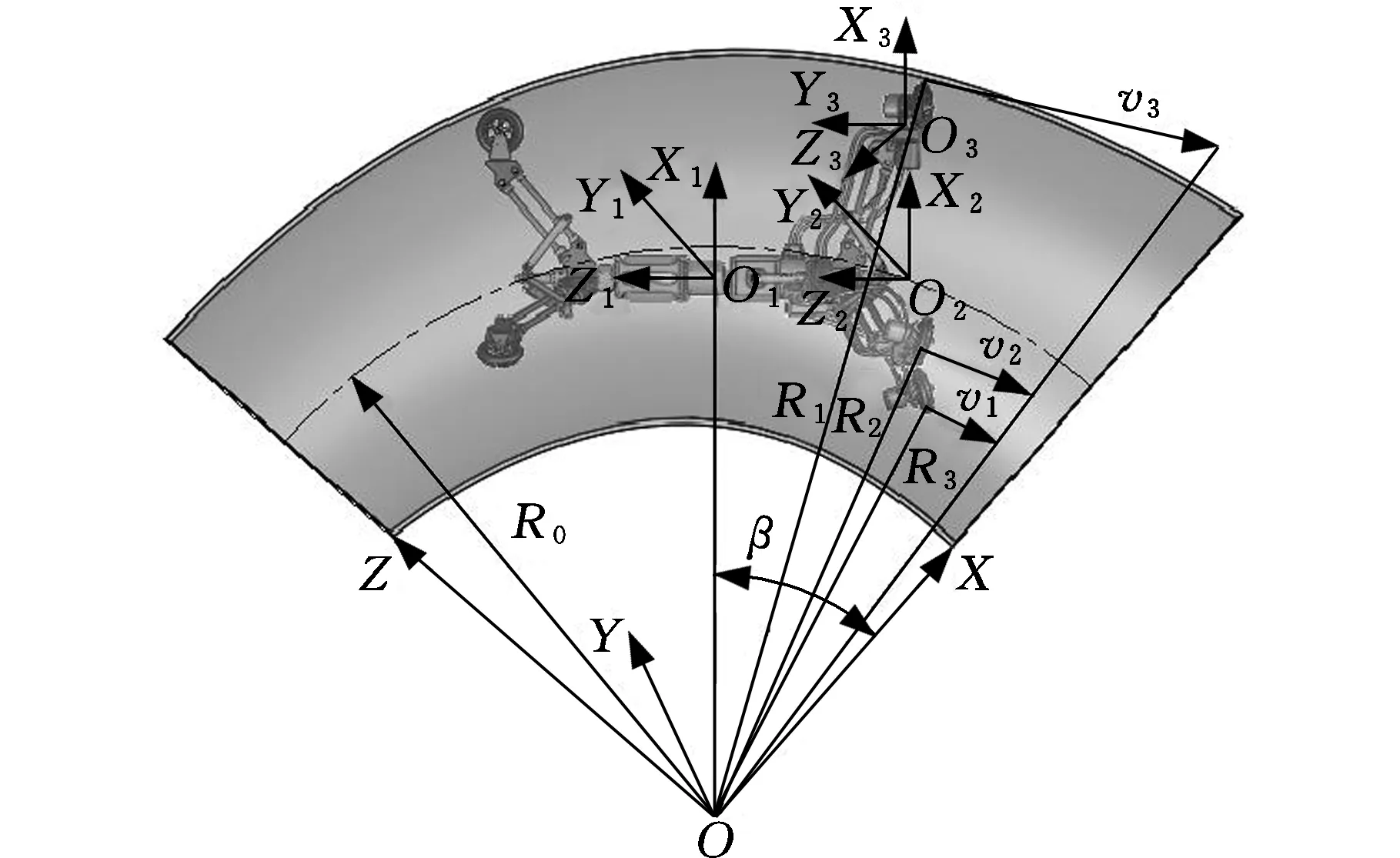
图5 变径弯管爬行工况示意图Fig.5 The diagram of curving variable diameter crawling conditions

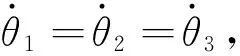
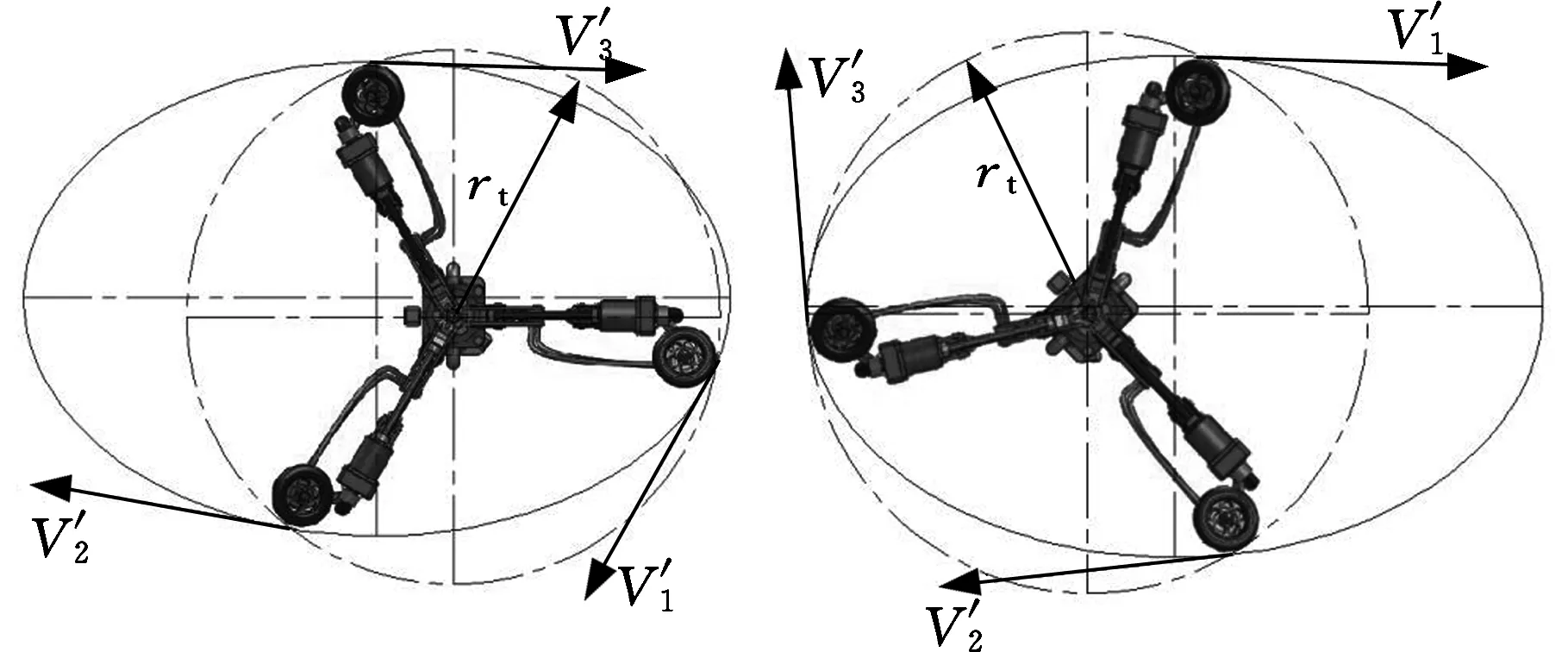
图6 螺旋驱动部分X2Y2面运动示意图Fig.6 The motion diagram of screw driver section in X2Y2 plane

v1∶v2∶v3=R1∶R2∶R3

(15)

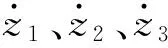
由以上分析可知,爬行装置在变径弯管内的运动过程中不出现打滑现象的必要条件如下：

(1)各驱动轮与管道内壁接触点的速度大小不断改变；

(2)各驱动轮对应的转角缸的三个偏转角度α1、α2、α3不断改变。

1.2 驱动机理

所提出的螺旋式驱动管道爬行装置的液压驱动机构如图7所示。

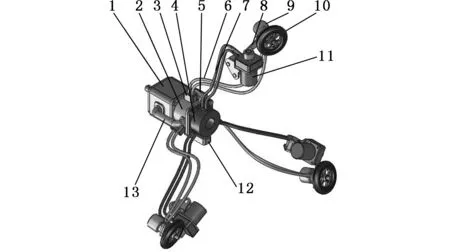
1.双向齿轮泵 2.主油路油池 3.限流器 4.转角调节油池 5.双向溢流阀 6.液压马达油管 7.转角缸油管 8.悬臂 9.微型液压马达 10.驱动轮 11.转角缸 12.油路选择开关 13.主油路油管图7 变截面管道爬行装置液压驱动机构示意图Fig.7 The hydraulic drive mechanism diagram of variable cross-section pipeline crawling device

液压驱动系统驱动原理如图8所示,整个驱动系统由一台电机通过联轴器驱动双向齿轮泵为整个系统的油路提供压力。按功能可将液压系统分为动力系统和转角调节系统。

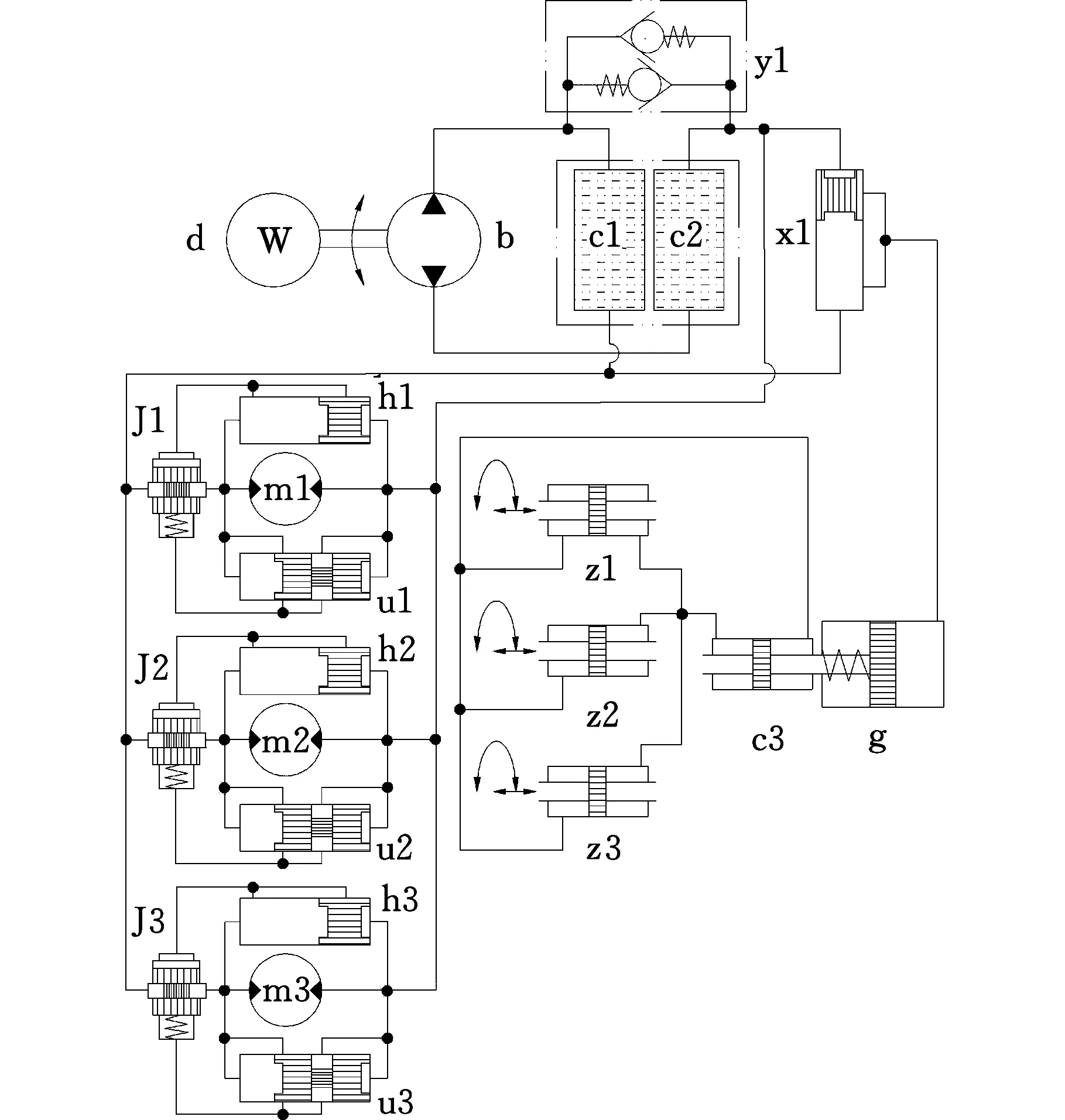
b—双向齿轮泵 ci—油池 y1—双向溢流阀 mi—液压马达 Ji—节流阀 x1—压力选择开关 zi—转角缸 g—推力缸 ui—低压选择开关 hi—高压选择开关(i=1,2,3)图8 变截面管道爬行装置液压驱动原理示意图Fig.8 The hydraulic drive mechanism schematic diagram of variable cross-section pipeline crawling device

1.2.1动力系统

由爬行装置在变径管内的运动规律可知,要避免驱动轮在运行过程中的打滑和运动干涉，驱动轮的转速需要与爬行装置的运动姿态和管道内壁的几何约束相适应,同时各驱动轮必须具有相对稳定的驱动力，从而推动整体机构的运行。

为解决驱动轮上述运动要求，爬行装置采取了图8所示液压驱动系统。双向齿轮泵b直接向主油路油池输入液压油，经过油池内c1和c2两个独立油腔(c1与c2间连接有双向溢流阀y1,用于限制主油路中的工作压力进行过载保护)将油路分解为三条并联的油路,分别驱动m1、m2、m3三台液压马达。由流体的连续方程可知泵与三台马达之间存在如下流量关系：

(16)

式中，vc为泵输出液压油在油腔内的平均流速；Sc为油腔截面积；vm1、vm2、vm3分别为m1、m2、m3接管内液压油平均流速；S1、S2、S3分别为m1、m2、m3接管截面积；qz为转角控制支路流量。

各驱动轮与管道内壁接触点的运动速度大小关系为

(17)

式中，vP1、vP2、vP3分别为各驱动轮与管道内的壁接触点的运动速度；Δq为液压马达每转动一圈所需排量。

由液体流动的最小能耗率原理可知，当一个流体系统处于平衡状态时，其能量损耗率的值会达到最小。在爬行装置运动过程中管道内的工况对驱动系统构成了不断变化的外界约束，迫使系统内部流体向能量损耗率值最小的方向流动，使驱动系统对于管内工况产生自适应的趋势,从而实现三个驱动轮的三轴差速运动模式，即

vP1≠vP2≠vP3

(18)

管道机器人在排空的管内巡检过程中经常会遇到因部分介质残留致使摩擦因数减小的管段,即驱动轮易打滑或空转的恶劣工况，这将使单个驱动轮以远大于其他两个驱动轮的转速打滑或空转，导致液压系统内部压力急剧下降，使其他两个驱动轮失去应有的驱动扭矩。针对此类问题本驱动系统对三台液压马达m1、m2、m3分别设置了由J1、h1、u1，J2、h2、u2和J3、h3、u3构成的三个独立的限流器。工作原理如图8所示。现以J1、h1、u1为例说明，油路选择开关h1和u1分别与m1两端连通，通过m1两端油路压差推动内部的滑块运动，分别选择m1两端油路中压力较高和压力较低的油路与节流阀J1两端连接(用于适应液压泵的正反转两种工况)，利用m1两端的压差控制流量阀的开度，限制m1支路的流量从而限制转速，保持油腔内的压力。由泵的输出特性可知：

W=ΔpvcSc

(19)

式中，Δp为泵两端压差；W为泵输出功率。

受到电机的功率和转速等本身机械特性限制，流量的增大将导致压力下降。图8所示液压系统通过三对并列油路驱动各马达，忽略管路的压力损失，则有：

(20)

且

Δp=Δp1=Δp2=Δp3

(21)

式中，Δp1、Δp2、Δp3分别为m1、m2、m3支路两端压差；ΔpJ1、ΔpJ2、ΔpJ3分别为J1、J2、J3两端压差；Δpm1、Δpm2、Δpm3分别为m1、m2、m3两端压差。

由节流阀流量公式可知ΔpJi与流量vmiSi有如下关系(i=1,2,3)：

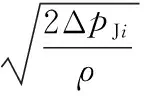
(22)

式中，ψ为流量系数；SJi为各节流孔流通面积；ρ为流体密度。

由马达的特性可知：

(23)

式中，FP1、FP2、FP3分别为各驱动轮在P1、P2、P3处的驱动力。

将式(22)、式(23)代入式(20)得

(24)

由式(24)可知,流量受液压系统本身的限制在有限范围内变化时,FPi和SJi是决定主油路工作压力的重要参数。其中FPi由外部工况决定。对于SJi则采用马达两端压差Δpmi对其进行闭环反馈调节，调节关系如下：

(25)

式中，εs为节流阀变截面系数；Sj0为节流阀最小流通截面；Sj为节流阀阀芯受压截面积；Fj为节流阀阀芯弹簧预紧力；kj为节流阀阀芯弹簧弹性系数。

将式(23)代入式(25)中得

SJi=

(26)

限流器以驱动轮的负载为输入变量通过式(26)对相应的节流阀开度进行调节，当负载减小时节流阀开度也随之减小，促使ΔpJi升高,阻止Δp下降的同时也对该支路的流量进行了限制，使液压系统达到新的平衡状态，有效防止了单一驱动轮打滑或空转导致系统的流量增大，导致主油路压力下降，并使其他马达两端压差降低从而失去应有驱动扭矩的作用。针对液压系统的特性对kj、Fj和Sj0等参数进行合理调正，可实现类似差速锁的功能，将驱动轮差速运动过程中的各速度比的值限制在所需要的范围内，可使系统更加稳定。

1.2.2转角调节系统

由1.1.2节的分析结论可知，为了避免螺旋式驱动管道爬行机构通过变径弯管的过程中出现打滑或运动干涉的现象，各驱动轮转角α必须随不断变化的外界约束而改变，以适应驱动系统的运动要求。转角调节系统采用图9所示的调节机构。

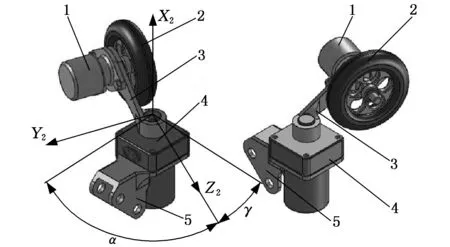
1.微型液压马达 2.驱动轮 3.悬臂 4.转角缸 5.支架图9 转角机构示意图Fig.9 The rotation mechanism diagram

该调节机构的调节原理如图8所示(坐标系与图3相对应)。转角调节系统由油路选择开关，转角调节油池g和z1、z2、z3三个转角缸构成。压力选择开关x1两端分别与主油路油池的两个内腔c1和c2连通，通过内部的滑块选择c1、c2中压力较高的油路驱动缸g，g驱动c3内活塞前后运动使其内部液压油流入并列驱动转角缸z1、z2和z3(g和c3共同构成了转角调节油池)；在运动过程中外部的几何约束通过驱动轮悬臂的扭矩传递到并联油路中，利用流体的流动特性实现角度的差值变化。

设转角缸的角度(初始角度均为零)与其两端流量有如下关系：

αzi=φzVzi

(27)

式中，αzi为转角缸的角度变化量(i=1,2,3)；φz为变动系数；Vzi为流经各转角缸的液压油体积。

忽略转角缸自身扭矩的影响，转角调节支路有如下调节关系：

(28)

式中，Sc3为缸c3截面积；Sg为缸g截面积；kg为缸g内弹簧弹性系数；Fg为缸g内弹簧预紧力;pg为缸g内的压力。

由能量守恒可得

(29)

式中，μ为有效功率系数。

直管内装置爬行过程中，有

FP=FP1=FP2=FP3

(30)

vP=vP1=vP2=vP3

(31)

由式(19)、式(23)、式(27)～式(31)得

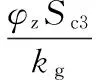
(32)

如图10所示,由变径直管的几何约束可知接触点P在很短的时间间隔Δt内的运动轨迹近似为直线AC(机器人质心运动轨迹为BD)，如不计摩擦损失，则由能量守恒，负载力Fz与驱动力FP之间存在如下关系：

Fz|BD|=FP|AC|

(33)

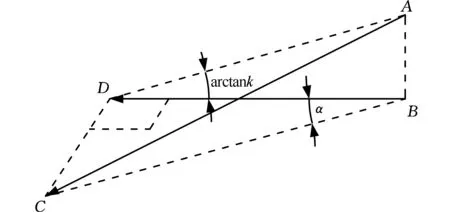
图10 接触点路径简化示意图Fig.10 The simplified diagram of contact point path

则由几何关系得到：

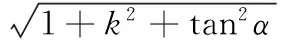
(34)

将式(32)代入式(34)中得

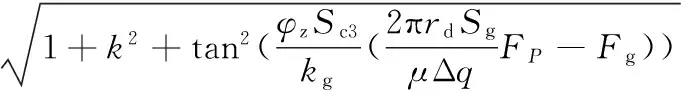
(35)

当爬行装置运动阻力增加时驱动轮的转速下降，由式(19)和式(23)可知这将引起驱动力FP的增大,负载能力调节分为两个阶段:

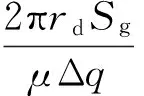
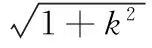
(36)

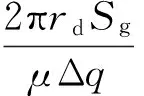
通过对上述爬行系统的运动机理研究，可知在直线和转弯过程均具有类似的调节机制，即利用系统内部压力感知外部负载变化，同时通过改变转角的方式控制驱动轮的负载能力，以更好地适应管道内部环境的约束。

2 驱动性能仿真分析

2.1 负载能力分析

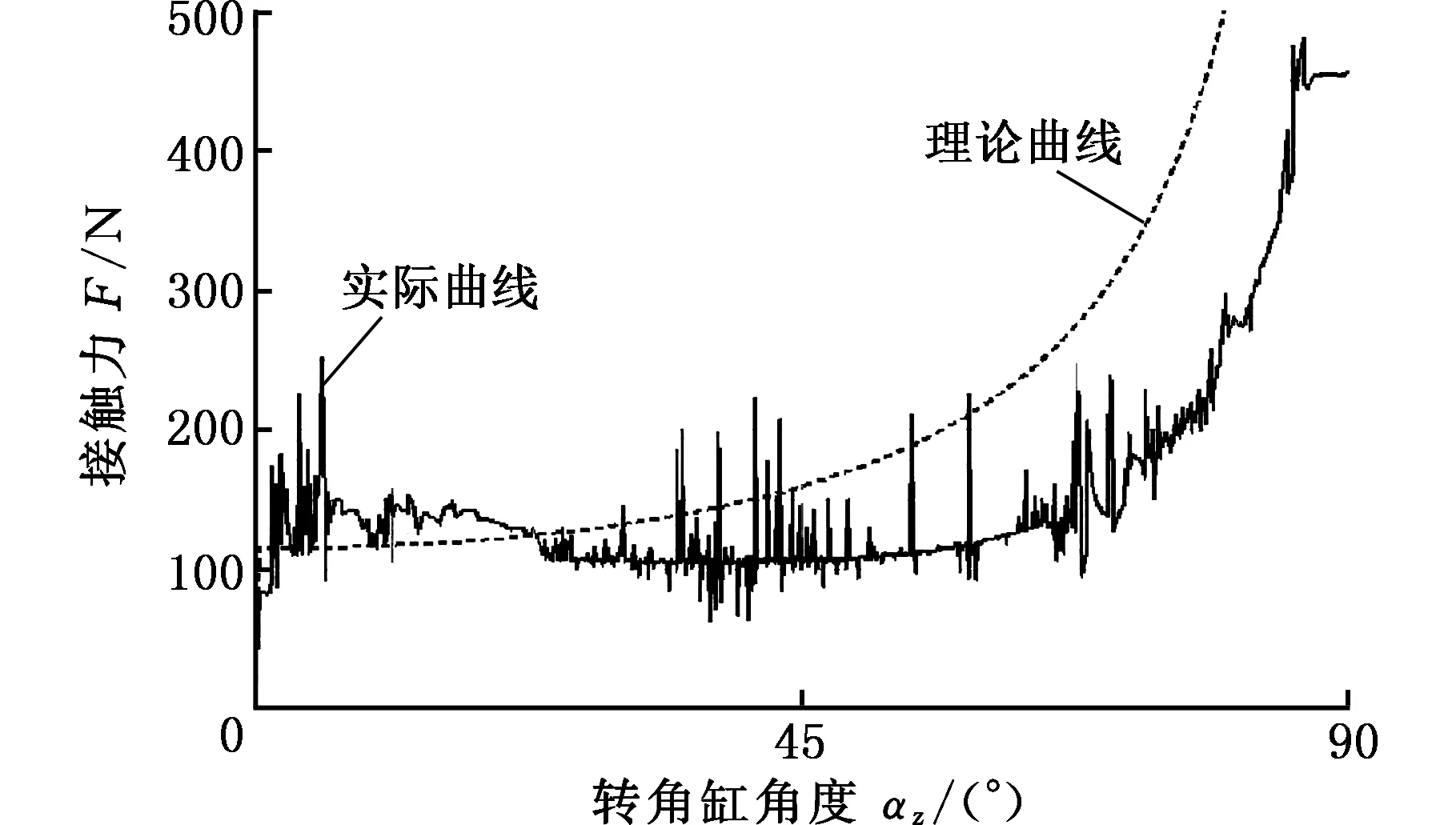
图11 接触力变化曲线Fig.11 The curves of contact force

针对式(34)的驱动力调节方程，在ADAMS软件中建立驱动轮半径rd=50 mm、各驱动轮扭矩M=2.5 N·m、管道变径系数k=0.1的分析模型。仿真过程中对图3中的直线变径管内爬行机构的前半部分进行了匀速约束。在上述参数条件下，对联轴器与齿轮泵输入轴在轴线方向上的接触力在转角αz从0°到90°变化过程中的大小进行测量，得到如图11所示变化关系。它的变化规律与预计基本相同，由于接触面的碰撞使接触力的大小产生了不同程度的波动。实际曲线为驱动力抵消变径管支撑力在轴线方向分力后的数值，故略低于理论值。仿真结果表明,通过增大αz可有效提高爬行装置的负载能力。

2.2 差动与限速分析

针对1.2.1节中提出的差速与限速机理，在AMESim中建立了如下仿真模型。液压系统参数为kj=1200 N·m、Fj=1 N和Sj0=0.04 mm2、节流阀最大开度SJmax=12 mm2、εs=3 mm、Sj=16 mm2，泵的额定流量为1 L/min。为了模拟运动过程中负载变化的情况下系统的响应，对三个马达的负载进行如下设置：①1～2 s，m1、m2和m3三台马达负载均为2.5 N·m；②2～6 s，m1负载由2.5 N·m按照一次关系逐渐减小到0，m1和m2负载不变；③6～7 s保持6 s末负载不变。

仿真过程中m1、m2和J1两端的压差变化关系如图12所示(m2和m3曲线基本重合，图中仅示出m2的数据)。

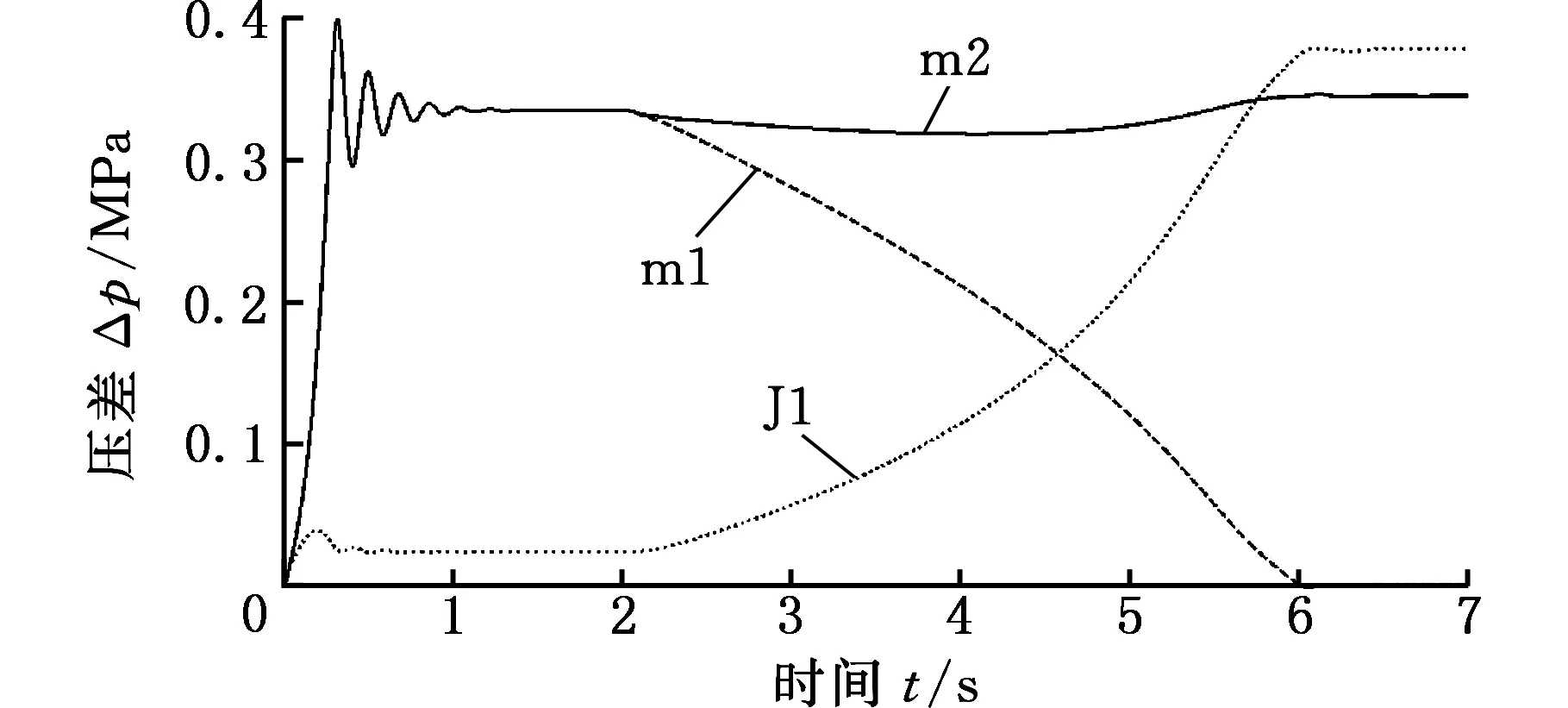
图12 压差变化曲线图Fig.12 The curves of changing pressure change

如图12所示：①1～2 s，系统启动达到稳定运行状态，m1和m2两端压差稳定在0.35 MPa左右；②2～6 s，m1负载逐渐减小过程中，其两端压差也随之减小，随着开度减小，J1两端压差逐步增大，m2和m3两端压差基本保持不变，由式(23)，在m1负载减小过程中，m2和m3保持了原有的驱动扭矩。

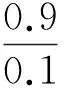
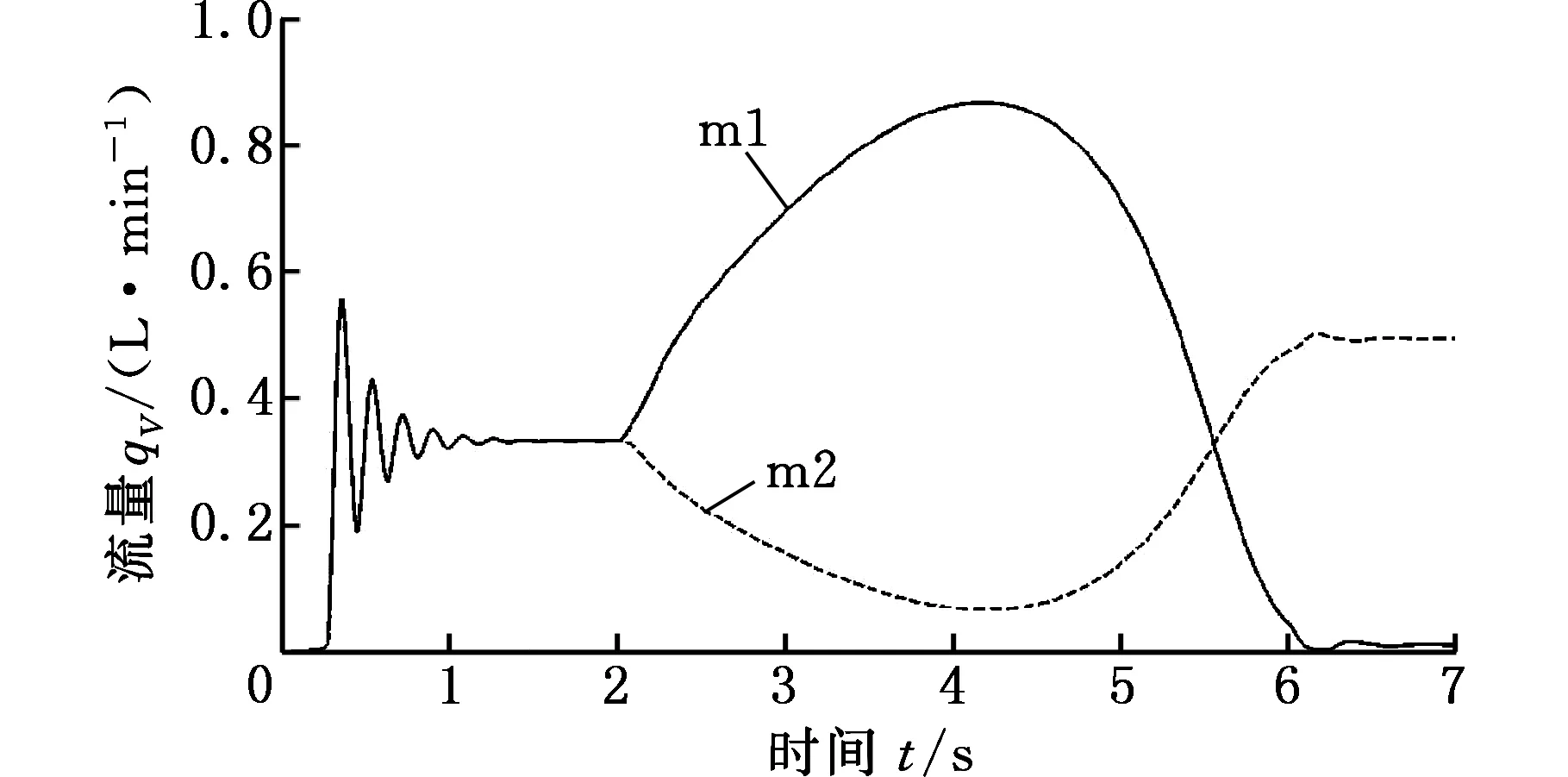
图13 流量变化曲线图Fig.13 The curves of changing flow

由上述分析结果可知,该驱动系统实现了驱动轮到三轴差速，同时可对差速比实施限制，使系统在单一驱动轴空转或打滑时对该轴的输出功率进行限制，从而使系统另外两轴保持应有的驱动扭矩。

3 试验研究

针对驱动系统三轴差动与限速的功能，采用如图14所示液压缸代替驱动马达,进行实验研究。其中Q1、Q2、Q3分别与马达m1、m2、m3相对应，节流阀F1、F2、F3分别与J1、J2、J3相对应；U1、U2、U3为负载缸，用于提供恒定负载以模拟m1、m2、m3对应的负载变化，各缸内压力ΔpUi与Δpmi(i=1,2,3)对应。为了模拟油路中的反馈调节机制，试验采用了与数学推导相结合的方式。首先，根据式(25)推导负载变化时调节模式下F1、F2、F3的一系列开度值；然后，调节F1、F2、F3至对应的开度；最后，采集系统稳定后的数据。利用F1、F2、F3不同开度条件下驱动系统的响应来研究反馈调解中的控制机制。

图14 差动试验原理Fig.14 Principle of differential test

试验主油路的输入压力为0.6 MPa，负载缸U1和U3油路压力为0.4 MPa，U2缸内油路压力从0.4 MPa线性逐级递减至0(步长为0.02 MPa),模拟驱动轮打滑时负载降低的过程。对此过程中Q1、Q2、Q3的运动速度进行了记录，结果如图15所示。

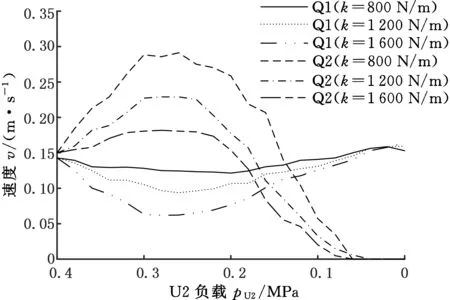
图15 差动试验的速度分布Fig.15 Speed distribution of differential test

由式(25)可知,kj是影响节流阀开度的重要参数，间接决定了反馈调节机制的响应。为了研究kj对系统响应的影响，分别对3组kj值(kj=800，1 200，1 600 N/m) 进行相应的试验。由于Q1和Q3运动接近同步，故图15中省略了Q3的数据，试验结构与仿真结果的响应规律基本保持一致。在kj不同的情况下出现了三种不同的相应曲线。当kj=1 600 N/m时，差速系统表现出了较好的自锁能力，在Q2负载减小时很快对其速度进行了限制，使Q1没有出现比较明显的速度波动；当kj=800 N/m时，差速系统表现出了较好的差速性能，在Q2负载减小时相对缓慢对其速度进行了限制，使Q1出现了比较明显的速度波动，实现了较大的差速比；当kj=1 200 N/m时，介于以上两种情况之间。由此，通过调整kj的值,可实现差动系统的不同响应，以满足不同工况的需要。

4 结论

(1)实现了驱动轮的三轴差速运动；同时采用各支路内的压差信号对其流量进行调节，限制了驱动轮打滑和空转时的功率输出，使驱动系统保持了所需的稳定扭矩。

(2)实现了各驱动轮螺旋转角的三轴差速运动，并以液压系统内部工作压力为信号感知机构在运动过程中的负载变化，对各转角缸角度进行调节，实现了传统驱动与螺旋式驱动之间的相互转化，从而对爬行装置整体驱动力实施调节，以适应外界负载不断变化的运动工况。

[1] REN Sijing, DONG Jinbo. Analysis and Research of Wandering and Procession Pipe Robot Driven by the External Magnetic Field[J]. Test and Performance,2010(3):3219-3221.

[2] 刘清友, 李雨佳, 任涛,等. 主动螺旋驱动式管道机器人[J]. 机器人,2014,36(6):711-718.

LIU Qingyou, LI Yujia, REN Tiao, et al. An Active Helical Drive In-pipe Robot[J]. Robot,2014,36(6):711-718.

[3] YAN Hongwei, KOU Ziming, GAO Bo. Based on Risk Source Tanks Leakage Adaptive Strong Magnetic Emergency Device and Sealing Method Research[J]. Applied Mechanics and Materials,2011,66/68:460-465.

[4] 许冯平, 邓宗全. 管道机器人在弯道处通过性的研究[J]. 机器人,2004,26(2):155-160.

XU Fengping, DENG Zongquan. Research on Traveling-capability of Pipeline Robot in Elbow [J]. Robot,2004,26(2):155-160.

[5] 张学文, 邓宗全, 贾亚洲,等. 三轴差动式管道机器人驱动单元弯管通过性研究[J]. 中国机械工程,2008,19(23):2777-2781.

ZHANG Xuewen, DENG Zongquan, JIA Yazhou, et al. Research on Traveling-capability of Drive Unit of Triaxial Differential In-pipe Robot in Elbow [J]. China Mechanical Engineering,2008,19(23):2777-2781.

[6] MAZZINI F, KETTLER D, GUERRERO J, et al. Tactile Robotic Mapping of Unknown Surfaces, with Application to Oil Wells[J].IEEE Transactions on Instrumentation and Measurement,2011,60(2):420-429.

[7] 窦刘良, 王丰, 冯丽艳,等. 高炉煤气管道检测机器人机构研究与ADAMS仿真分析[J]. 机床与液压,2016,44(23):30-33.

DOU Liuliang, WANG Feng, FENG Liyan, et al. Mechanism Research on Blast Furnace Gas Pipeline Inspection Robot and ADAMS Simulation Analysis [J]. Machine Tool & Hydraulics,2016,44(23):30-33.

[8] Welltec.Coiled Tubing Well Tractor[DB/OL]. [2013-12-01].http://www.welltec.com/Coiled-Tubing-Well-Tractor.aspx?ID=106.

[9] Omega Completion Technology Ltd. Omega. Innovative Down-hole Tools for the Oil & Gas industry[DB/OL].[2013-12-17].http://www.omega-completion.com/tractor.html.

[10] 施绍宁. 新型管道除锈机行走部弯管通过性的研究[J]. 机械设计与研究,2012,28(3):94-98.

SHI Shaoning. Research of Curved Pipe’s Passing Nature about a New Pipe Rust Maching [J]. Machine Design & Research,2012,28(3):94-98.

[11] JUNGWAN P，TAEHYUN K,HYUNSEOK Y. Development of an Actively Adaptable In-pipe Robot[J]. Proceedings of the 2009 IEEE International Conference on Mechatronics.Malaga,2009:1-6.

[12] ROMAN H T, PELLEGRINO B A, SIGRIST W R. Pipe Crawling In-spection Robots: an Overview[J]. IEEE Transactions on Energy Conversion,1993,8(3):576-583.

[13] ROH S G, KIM D W, LEE J S, et al. In-pipe Robot Based on Selective Drive Mechanism[J]. In Proceedings ICMET,2011,7(1):105-112.

[14] ANDRZEJ S. Leak Detection in Liquid Transmission Pipelines Using Statistical Analysis [J]. Diagnostyka,2013,14(1):71-77.

[15] KAKOGAWA A, MA S G. Experimental Verification of Analytical Torques Enabling a Screw Drive In-pipe Robot to Pass Through Bent Pipes[C]//IEEE International Conference on Robotics and Biomimetics. Piscataway: IEEE,2011:1742-1747.

[16] HORODINCA M, DOROFTEI I, MIGNON E, et al. A Simple Architecture for In-pipe Inspection Robots[C]//Proceedings of the International Colloquium on Autonomous and Mobile Systems. Magdelburg,2002:61-64.