基于信度加权叠加分布模型的医疗保险损失数据拟合问题研究

郭建平，赵立龙

(南京信息工程大学 a.管理工程学院；b.中国制造业发展研究院；c.物理与光电工程学院，江苏 南京 210044)

一、引 言

医疗保险的被保险人接受医疗服务后可以获得部分或者全部医疗费用的补偿，这部分被补偿的医疗费用通常被认为是医疗保险损失。对医疗保险损失的准确估计是确定医疗保险产品相关费率的基础，而识别医疗保险损失数据分布形式是精算师们厘定相关医疗保险产品费率的重要步骤之一。依据传统损失分布理论，医疗保险损失分布模型拟合的优劣往往取决于经验分布函数的选择和参数的估计。医疗保险损失的信息往往不完整并且损失数据不充分，致使经验函数的选择有时会出现较大偏差，参数估计结果也会因为估计方法不同而不同。有时参数估计结果差异较大，难以确保损失分布模型与实际损失数据生成过程相互匹配，拟合效果不理想，致使后续保险产品费率的精算结果与实际损失情况有较大偏离。如何科学厘定医疗保险相关产品的费率，如何合理确定保险准备金关乎着保险公司的正常经营以及投保人的利益，解决这些问题的基础是寻找真实反映医疗保险损失的分布规律。

获得一组医疗保险损失数据后，通过观察数据的分布形态，尤其是尾部特征，结合对数据分布的初步分析，可以选用一些常用理论分布模型来拟合。现有研究经验和成果普遍认为医疗保险损失数据的分布呈现出非正态且右偏的显著特征，常常带有一条长长的厚厚的尾巴，“厚尾”形态反映了小概率事件发生的高额赔付，尤为保险人所重视。

医疗保险精算通常采用双参数和多参数的分布模型来拟合医疗保险损失数据，其中伽玛(Gamma)分布、对数正态(Lognormal)分布、帕累托(Pareto)分布、韦伯(Weibull)分布和布尔(Burr)分布应用比较广泛。上述各种理论分布模型对医疗保险损失数据尾部的拟合效果各有不同。伽玛分布密度函数图像呈现右偏特征，其尾部比指数分布的尾部相对为厚，对数正态分布的密度函数趋于零的速度慢于伽玛分布，具有比伽玛分布更厚的尾部。在拟合高额损失数据偏多的样本时，对数正态分布的拟合效果比伽玛分布理想。相对于伽玛分布而言，帕累托分布的右偏程度更为显著，但是尾部不一定很厚，致使帕累托分布经常对超过均值的损失数据存在过度拟合的问题，韦伯分布当参数τ>1时，趋于零的速度很快，尾部很薄，在一定条件下发生特大赔付的概率很小，存在低估极端损失的倾向；而当τ=1时，韦伯分布退化为指数分布。布尔分布在社会医疗保险中也经常用到，帕累托分布是其特例。

由于医疗保险损失数据的实际数据生成过程比较复杂，实际精算实践中很难找到与医疗保险损失数据匹配非常好的单个理论分布，一些理论分布如指数分布等模型对损失数据的尾部拟合不足，通常是低估了小概率事件发生的概率，致使对大额损失估计偏低；同时，尾部较厚的分布，如帕累托分布，可能存在对尾部的过度拟合。基于以上对常用分布的理论分析，Jacques和Stuart提出用两个或者多个理论分布的加权来拟合医疗保险损失数据，使其尾部能够更加真实地反映实际数据的分布特点[1]。由两个或两个以上分布形成的分布模型也被称为叠加分布或者组合分布，本文使用叠加分布来表述此类模型。

二、分布模型的研究文献概览

大量研究者对不同领域的数据拟合问题做了卓有成效的研究，取得了丰富的成果。吴岚和王燕对损失数据的常用分布形式进行了分析，探讨了分布性质，研究了参数估计问题，设计了拟合不同损失数据的一般方法[2]16-27。韩天雄系统分析了常用分布的应用情景，给出了理论损失分布相关参数的估计方法[3]34-48。具有厚尾特征数据的分布拟合问题被研究者着重关注，如仇春涓等考察了厚尾分布下医疗保险保费合理性问题[4]。这些研究为后续进一步探索数据拟合问题奠定了坚实的基础，但是这些研究主要基于单一理论分布模型而展开分析，存在着潜在的拟合不足或者过度拟合的问题。

为了解决拟合不足或者过度拟合的问题，研究者通过构建叠加分布模型，探索了损失数据的拟合问题并比较了叠加分布模型和传统单一分布模型的拟合效果。如孟生旺和徐昕讨论了负二项回归模型、泊松一逆高斯回归模型、泊松一对数正态回归模型、泊松回归模型、双泊松回归模型、混合负二项回归模型、混合二项回归模型并做了系统比较研究[5]。赵桂芹等提出了通过帕累托分布与广义帕累托分布组成混合模型对具有“双峰”或“多峰”特征的损失数据进行拟合的思想[6]。此外，另有部分研究者在分布拟合问题研究的基础上，结合统计分析工具和现代经济计量思想，进一步探索了分布拟合模型的各种应用价值[7-9]。

上述研究成果基本可以概括为两类，一类是单一使用一种理论分布形式进行数据的拟合。保险损失数据的一个重要特点是尖峰厚尾性，即既有大量的小额损失，又有少量的高额损失，使得通常的单一损失分布模型很难准确拟合此类数据。另一类研究者把两个或两个以上的单一分布合成一个叠加分布模型，通过叠加分布模型对各种损失分布数据进行拟合，这日益成为关注的重点领域。通过对分布模型的拟合研究，进一步展开后续保费费率厘定以及责任准备金等问题的应用分析。上述研究进一步丰富了数据分布的拟合问题，为进一步探索医疗保险损失数据的分布形式奠定了坚实的基础。

通过梳理叠加分布模型的研究文献，发现如何匹配叠加分布模型中单一分布的权重参数并没有取得统一的认识，大量研究获得包括权重参数在内的待估参数的方法主要是利用数值优化技术。通过数值优化技术获得的权重参数实际意义不明确，同时增加了一个未知参数也增加了估计的难度。本文创新性地利用信度理论思想，通过保险损失数据期望和方差等信息，获得信度因子，把信度因子作为单一分布的权重参数拟合叠加分布模型，通过充分利用损失数据的各类型信息，更加准确匹配实际损失数据的发生规律。

三、建模过程

(一)单一分布判别

单一分布是构成叠加分布的基础，获得一组数据之后，需要确定数据适用的单一分布形式。确定一批数据适用某种分布的主要步骤是：首先根据观测得到的数据编制损失经验分布并绘制经验损失分布图；然后根据经验损失分布图的形态特点选择与之最相似的理论分布族；最后，对选定的理论分布参数进行参数估计，确定与实际数据相互匹配的理论分布。

实际分析过程中，可以通过绘制频率密度直方图并匹配相应的拟合分布曲线进行判断，也可以用P-P概率图和Q-Q概率图。P-P图是根据变量的经验分布与指定分布的累积分布函数之间的关系绘制的图形，Q-Q图是用样本数据的经验分位数与所指定分布的分位数之间的关系曲线来进行检验，两者均可以直观判断损失数据是否较好服从某一分布。

医疗保险损失数据具有显著的厚尾特征，需要使用平均剩余期望函数对尾部进行细致的考察。平均剩余期望函数通常被定义为：eX(d)=E[X-d|X>d]，其中X表示损失随机变量，d表示免赔额。如果平均剩余期望函数随d递增，在变量取值较大处的期望结果会很大，概率向右移，则表明损失变量X的尾部相比那些平均剩余期望函数递减或增速较慢的分布的尾部更厚。反之，如果平均剩余期望函数随着d递减，说明损失变量X为轻尾分布。本文使用样本经验剩余期望函数来分析损失数据的尾部特征，肖争艳和孙佳美定义样本经验剩余函数如下[10]50-56：

(1)

(2)

将给定的一组医疗保险损失分布数据代入公式组(2)，计算出经验剩余函数值。然后，对应于这组损失分布数据作出经验剩余函数的散点图并将该图与几种常用分布图加以比较，从而初步判断出该组数据近似服从的分布类型。

(二)信度因子确定

信度理论是研究如何正确、合理地处理先验信息和后验信息，即研究如何通过加权把两者综合起来的理论。信度理论萌芽于20世纪20年代。最早的信度理论被意外险精算师应用于计算劳工赔偿险费率。

假设X是损失随机变量，x1，x2，…，xn是其观测值，在非寿险精算中经常把X的数学期望E(X)=μ或者对将来损失的估计值作为厘定费率的依据。一般而言，总体均值μ是未知的，通过有限个观测值n来推断总体均值μ必定会产生误差，但是随着观测值个数n的不断增加，推断产生的误差可以越来越小，当观测值个数n足够大时，样本均值与总体均值μ充分接近。设α和γ为预先给定的比较小的正数，若n满足式(3)：

(3)

则称n满足完全可信性条件，取显著性水平α=0.05，则不等式表示相对误差不超过一个指定小的数γ的概率大于95%，并且根据不等式可得满足完全可信条件的n的最小值。

(4)

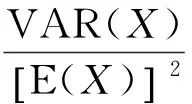
但是，保险实践中实际观测数据量很可能小于完全可信时候的最小观测数据量，为了使得相对误差标准不等式(3)仍旧成立，在式(3)中乘上了一个介于0～1之间的修正系数Z，即信度因子，变形如下：

(5)

由于Z介于0～1之间，因此，式(5)可以成立。类似上面的推导过程，可以得到信度因子Z的解析表达式。

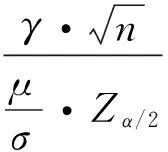
(6)

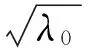
(7)

根据信度因子的推导过程和表达式可知，信度因子综合了样本期望和方差以及观测个数的信息，有助于更好地推测和判断数据分布的相关特征。对于给定的样本数据，通过方差和期望的计算，容易获得信度因子，如果把信度因子作为权重引入叠加分布模型，有可能提高数据拟合精度。

(三)参数估计

根据步骤(一)和(二)的论述以及引言中对精算实践中常用理论分布性质的分析，选择对数正态分布和伽玛分布作为单一分布并计算出信度因子，构造的对数正态伽玛(Lognormal-Gamma)叠加分布模型的分布密度函数为：f(x)=Z·f1(x)+(1-Z)·f2(x)，其中Z为式(7)定义的信度因子。对于离散数据，分布密度f(x)应理解为分布函数即F(x)。

由于对数正态分布和伽玛分布密度函数中分别含有两个未知参数，叠加分布密度中共有四个待估参数。当前研究估计这些参数的主要方法是利用计算机进行数值迭代，通过满足一定的收敛标准确定最优值。但是，不合适的迭代初始值常常使得迭代程序不收敛，因此选择一个相对准确的初值对于成功估计参数具有重要意义。极大似然估计作为一种精确的参数估计方法理应首先考虑，但是叠加分布模型是一种加法模型，对数运算处理加法模型没有优势，因此，没有使用极大似然方法估计参数。矩估计也是常用的参数估计方法之一，其基本思想是求解参数使得样本分布的各阶原点矩等于理论分布的各阶原点矩。除此之外，分位点估计法也是常用的参数估计方法之一，其基本思想是构造一个模型使其分布分位点与实际样本的分位点相匹配。这里权衡考虑三种方法的计算便捷程度和信息利用的充分程度，选择了矩估计法对参数进行估计。使用矩估计法进行估计时需要计算理论分布的各阶原点矩，为计算简洁，通过构造矩母函数来生成各阶矩，完成矩估计。

定义矩母函数：设随机变量X的分布密度函数为f(x)，其矩母函数为：

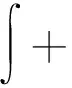
t≥0

(8)

记X的k(k=1，2，…)阶原点矩为pk=E(Xk)，则有：

(9)

即理论分布的各阶原点矩分别是矩母函数在零点的导数值。通过矩母函数可以方便计算出理论分布各阶的原点矩，叠加分布模型的矩母函数为：

MX(t)=E(etX)

f2(x)]dx

(10)

(四)拟合效果分析

对于得到的分布模型，通过实际值与各种分布拟合值靠近程度的比较可判断拟合效果优劣。针对某些特定分位点拟合情况，为了对厚尾数据的尾部性质进行细致观测，本文给出了尾部观测的分位点拟合值。通过理论分析可以认为叠加分布由于考虑了数据的期望和方差以及误差精度之间的内在联系，因而对数据的拟合效果理应优于单一分布的拟合效果。

四、实证分析

(一)样本数据说明

使用理论分布对观测数据进行数量分析具有显著优势，通过较少几个参数(数字特征)就可以概括样本数据分布情况，简化计算，并且理论分布具有良好的分析性质，微积分等数学工具可以充分使用。因此，即便样本数据很充足的情况下，有些问题仍需要使用理论分布进行分析。在统计实践中存在着大量的尖峰或厚尾或偏态的观测数据，这类样本数据显著背离正态分布，如果用以正态分布为核心的传统统计分析方法进行分析，结果往往令人质疑。在保险精算实践中也经常发现单个理论分布对具有尖峰厚尾特征数据的拟合效果不尽如人意，厘定的产品费率时常背离实际情况。因此，有必要建立处理“特异”数据的新概率分布模型以及相关分析方法，叠加分布模型就是其中的研究内容之一，叠加分布模型通过加权的方法对若干单一分布拟合不足或者拟合过度的问题进行修正，用于拟合具有高度复杂性和变异性的观测数据，能够提高“特异”样本数据的拟合精度。

医疗保险损失数据具有高度的复杂性和变异性，对医疗保险损失数据分布的准确拟合是医疗费用评估的基础，现有研究普遍认为医疗保险损失数据的分布呈现尖峰厚尾形状，既有大量的小额损失数据，又有较多的巨大损失数据，并且由于数据删失和死亡事件等因素的影响，致使医疗保险损失数据的拟合变得愈发复杂，通常的单一分布模型已经很难准确拟合医疗保险损失数据，叠加分布模型自然成为可供选择的分析方法之一。这里选择了某公司一批医疗保险损失数据，用于比较叠加分布模型和单一分布模型拟合样本数据的优劣。原始医疗保险赔付支出损失数据见表1，相应损失变量记为y。

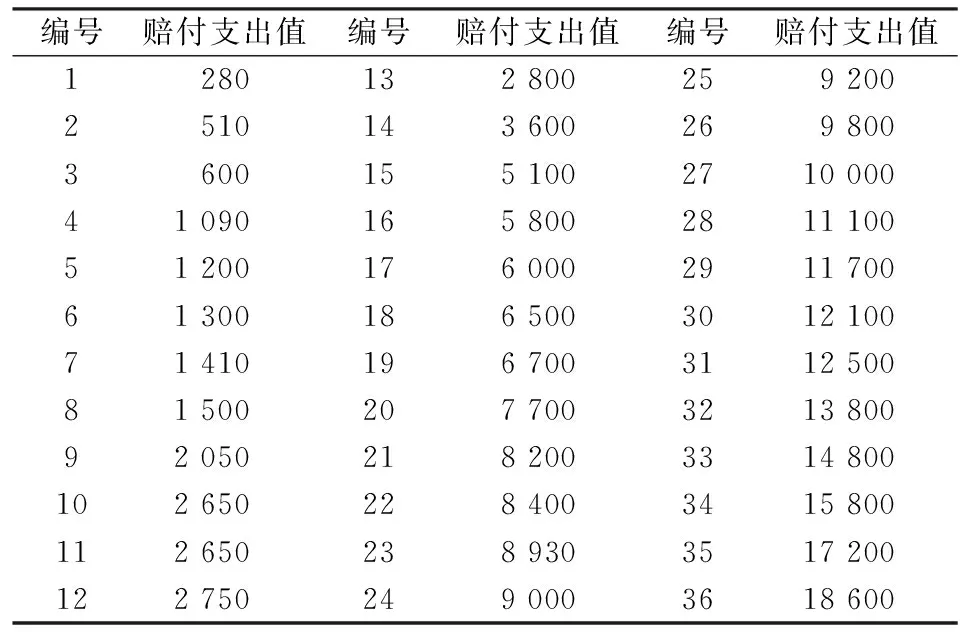
表1 医疗保险赔付支出损失数表 单位：元

(二)模型建立

1.描述性统计分析

以下主要使用SAS系统进行计算，由表1计算变量的描述性统计分析结果见表2。

根据偏度系数可以判断这批数据存在右偏趋势，由峰度系数可以判断数据尖峰特征不明显。为了直观上对损失数据分布规律进行把握，也可以根据损失数据取对数以后的直方图加以判别。另外，通过上文介绍的经验剩余函数值的计算，利用经验剩余函数图也能判断出数据具有厚尾特征，限于篇幅这里省略了相关分析过程。

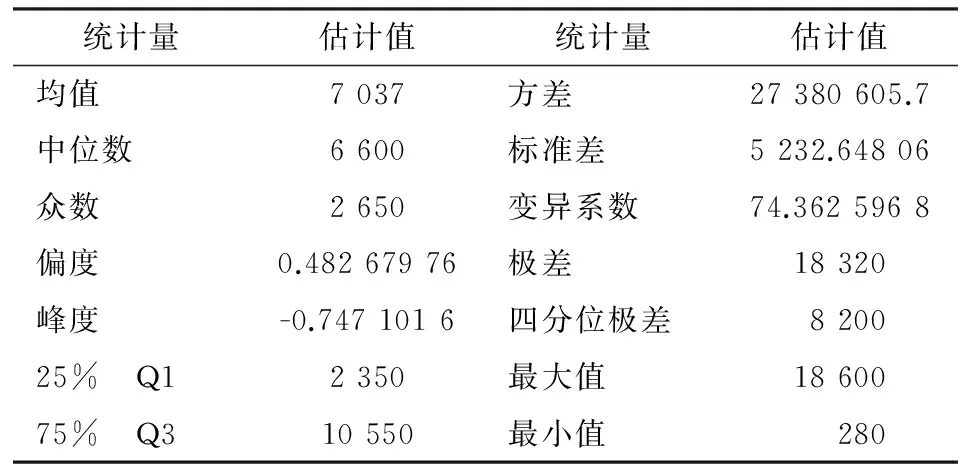
表2 描述性统计分析表

2.单一分布的拟合优度检验

根据数据分布特征，给出了对数正态和伽玛分布两条拟合曲线，检验统计量见表3。

由表3可知对数正态分布所有三种拟合优度检验统计量及其概率值在显著性水平为0.05时均显著，故这批数据用对数正态分布拟合不适合；伽玛分布的K-S统计量在0.05显著性水平上不显著，但另两个统计量显著，综上认为这批数据用对数正态分布或伽玛分布单一的分布形式来拟合并不恰当。为便于和叠加分布模型的拟合结果相互比较，给出了单一对数正态分布和伽玛分布的尾部部分分位数拟合值，见表4。

表3 拟合优度检验表

表4 单一分布分位数拟合值比较表

在表4中，50%的百分比即为中位数，本案共36个观测值，排序以后，中位数位于(n+1)/2=18.5位置处，即第18和第19个观测值(6 500和6 700)之间的0.5位置处，取(6 500+6 700)/2=6 600。其余各个分位点上的观测值同样计算。

3.信度因子的计算

根据上文所述，使用信度因子进行分布加权。假设显著性水平α=0.05，指定小的数γ=0.1，则Zα/2=1.645，λ0=(Zα/2/γ)2=1 082.41，给定样本数据的均值为7 037，方差为27 380 605.7，完全可信条件下的最小观测个数为：

由于无法确定先验信息，可以构建的叠加分布模型有两个，分别如下：

模型(1)f(x)=0.245 0·f1(x)+

(1-0.245 0)·f2(x)

(11)

模型(2)f(x)=(1-0.245 0)·f1(x)+

0.245 0·f2(x)

(12)

模型中的f1(x)和f2(x)分别为对数正态分布和伽玛分布的密度函数。

(三)参数估计

将相应参数带入模型(1)和模型(2)，得到理论分布的一至四阶各阶原点矩解析式。以模型(1)为例说明。

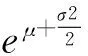
E(X2)=0.245 0·e2μ+2σ2+(1-0.245 0)·

α(α+1)θ2

α(α+1)(α+2)θ3

E(X4)=0.245 0·e4μ+8σ2+(1-0.245 0)·

α(α+1)(α+2)(α+3)θ4

(13)

计算样本分布的一至四阶各阶原点矩如下：

(14)

令样本分布的各阶原点矩等于理论分布的各阶原点矩，使用计算机数值计算方法得到四个参数α、θ、μ和σ的值。为便于比较，单一分布的参数拟合结果也列于表5中。

表5 信度加权的叠加分布的参数估计表

最终模型如下。单一对数正态分布密度函数：

x>0

(15)

单一伽玛分布密度函数：

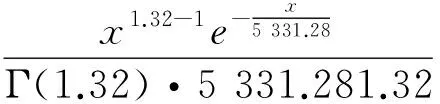
α>0，θ>0，x>0

(16)

由于估计值α=1，伽玛分布实际上退化为指数分布，信度加权的叠加分布密度函数如下：

(17)

(四)拟合效果比较

为了比较叠加模型对数据的拟合效果，令信度加权叠加分布密度函数分别等于相应的分位点概率值，得到分位点估计值见表6。

表6中，叠加分布分位数估计值的计算首先按照信度因子匹配相关的概率，如50%，分解为50%×0.245=0.122 5，50%×(1-0.245)=0.377 5。然后计算0.122 5对应的正态分布的分位点为-1.162 58，令Ln(x)=8.48+0.58×(-1.162 58)，取以e为底的指数求出x为2 430.14；令F(x)=0.377 5，容易求出指数分布对应的x为4 680，相加得到7 110.5。余下各个分位点的估计值同样可以求出。由表6结果可知由于反映均值和方差信息的信度权重修正，叠加模型的尾部拟合值更加接近观测值。相对于单一分布模型而言，使用叠加模型对厚尾特征的损失数据进行拟合研究结果将更加可靠。

表6 叠加分布模型分位点估计值表

在统计推断中，稳健性反映了现实样本数据与模型假定之间有偏差时算法结果的稳定性，度量了算法本身对其假定条件之偏差的敏感程度。本文提出的模型拟合方法使用的样本数据为具有显著非正态特征的医疗保险损失数据，因此模型拟合方法的分析结果对数据样本的分布形态(正态分布或者非正态分布)不敏感；并且信度因子计算中涉及的样本期望和方差的计算同样也不涉及数据分布形态，模型拟合方法的分析结果是稳健的。

五、结 论

准确判断与样本数据相匹配的理论分布的类型对于研究随机现象具有重要意义，确定理论分布的类型，可以运用统计分析方法估计理论分布中的未知参数，得到理论分布模型的解析表达式，即分布密度或者分布函数，计算随机变量的数字特征，完成统计推断并做出统计决策等一系列分析过程。

本文以医疗保险损失数据为样本研究了具有厚尾特征的观测数据的分布拟合问题，由于医疗保险损失数据的经验分布曲线很难用现有的单一常见分布拟合，经过多种方法的比较和计算，采用了由Lognormal分布和Gamma分布基于信度因子加权形成的Lognormal-Gamma叠加分布模型拟合医疗保险损失数据。数值计算的结果表明信度加权的叠加分布模型显著提高了拟合精度，这有助于精算师拟定精算假设，设计保险产品，合理厘定费率，形成正确的产品价格，即使是在制造业和工程应用等领域，本文提供的信度加权的建模思想也为分析数据的分布形态提供了有益借鉴。

[1] Jacques Rioux，Stuart Klugman.Toward a Unified Approach to Fitting Loss Models[J].North American Acturial Journal，2006,10(1).

[2] 吴岚,王燕.风险理论[M].北京:中国财政经济出版社,2006.

[3] 韩天雄.非寿险精算[M].北京:中国财政经济出版社,2010.

[4] 仇春涓,陈滔,吴贤毅.重尾分布下医疗保险保费合理性评估—基于上海市阂行区新农合的实证研究[J].数理统计与管理,2013,32(6).

[5] 孟生旺,徐昕.非寿险费率厘定的索赔频率预测模型及其应用[J].统计与信息论坛,2012,27(9).

[6] 赵桂芹,王上文.具有“双峰”现象损失数据的分布拟合[J].山西财经大学学报,2006,28(6).

[7] 刘家福,吴锦,蒋卫国,占文凤.基于泊松-对数正态复合极值模型的洪水灾害损失分析[J].自然灾害学报,2010,19(6).

[8] 卓志,王伟哲.巨灾风险厚尾分布:POT保险模型及其应用[J].保险研究,2011(8).

[9] 王明高,孟生旺.尖峰厚尾保险损失数据的统计建模[J].数学的实践与认识,2014,44(22).

[10] 肖争艳,孙佳美.精算模型[M].北京:中国财政经济出版社,2010.