基于相关熵的扩频周期估计方法
2018-01-15孙玖玲姬红兵
金 艳, 孙玖玲, 姬红兵
(西安电子科技大学电子工程学院, 陕西 西安 710071)
0 引 言
直接序列扩频(direct sequence spread spectrum, DSSS)信号采用扩频序列将信号频谱展宽,以满足传送带宽远远大于发送信息所需带宽的条件,降低了发射端信号的功率谱密度,使得信号能够在低信噪比情况下传播,因而直扩信号有很好的抗干扰性和抗截获性,广泛应用于军事通信、卫星通信和卫星导航等系统中。在非合作通信中,直扩通信的这些优点给信号的检测和参数估计带来了新的挑战。准确估计出接收信号的载频、码元速率、扩频周期及扩频序列等参数是完成信号的解调、解扩处理以及实现原始信号的捕获的前提。
其中,扩频周期的精确估计能够更好地完成后续扩频码的估计工作,因此实现扩频周期估计是非常重要的一步。针对扩频周期估计问题,文献[1]根据伪随机码良好的相关性和周期特性提出了相关检测法,由接收信号相关函数的峰值间隔即可估计出扩频周期;文献[2]基于自相关提出了波动相关法,选择合适的滑动窗对接收数据无重叠分段,由各段数据自相关二阶矩累加平均的峰值间隔可估计扩频周期。在国内研究中,文献[3]提出了基于四阶统计量的2-D切片法,高阶统计量可以很好地抑制高斯噪声,能达到较低信噪比容限,但其计算量较大;文献[4]提出的倒谱法,对输入信号的功率谱进行对数运算后再求其功率谱,在信噪比大于-12 dB的情况下能得到准确估计;文献[5-7]提出二次谱处理方法,即对信号的功率谱作二次功率谱处理,在周期处得到谱峰;文献[8]提出用四阶累积量与二次谱相结合的方法,利用接收信号的四阶累积量一维切片代替信号的相关函数做二次功率谱检测,对高斯白噪声有更好的抑制效果,但依然存在计算量大的问题。
文献[9]提出了相关熵理论,相关熵可以看成是基于Parzen核估计Renyi二次熵的一种退化表示,广泛应用于信道的盲均衡、时延估计等[10]领域。同时其又能够反映两个随机变量的相似度,因此相关熵也可用于估计由信号传输远近的不同而引起的信号时延。本文首先由相关熵定义,结合直扩信号模型分析了其隐含的周期性,据此提出一种估计扩频周期的相关熵法,然后针对信息码对扩频周期估计的影响,引入延时相乘处理,得到一种改进方法。仿真实验验证了基于相关熵的算法可在低信噪比下准确估计出扩频周期。
1 基于相关熵函数的扩频周期估计
1.1 信号模型
1.1.1 短码直扩信号
假设以扩频码速率Rc对信号采样得到离散时间短码直扩信号模型为
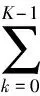
(1)
式中,A表示信号幅度;τ为传输时延对应的离散采样值;n表示采样时刻序号;b(k)、c(k)分别表示信息码和扩频码,取值均为1或-1;v(k)表示均值为零、方差为σ2的加性高斯白噪声;由于扩频码速率为Rc,则Tc=1/Rc为扩频码时宽;假设扩频周期T0等于L倍扩频码元宽度,即T0=LTc。此时,短码的每一位信息码对应一周期扩频码。
1.1.2 长码直扩信号
对接收的长码直扩信号以扩频码速率Rc采样后可表示为
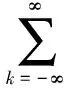
(2)
式中,A、n、L、c(n)、v(n)定义与短码直扩信号相同;b(n)表示离散的信息码波形,信息码元速率可以表示为Rb,信息码元宽度Tb=1/Rb,则b(n)可以表示为
(3)
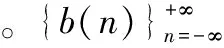

(4)
定义扩频调制比M=L/G,表示每周期扩频码对应调制的码元个数,当G
1.2 相关熵及其性质
相关熵是一种广义的相关函数,对于随机过程{Xt,t∈T},T为时间集合,则其相关熵可定义[11]为
Vσ(t1,t2)=E[kσ(Xt1,Xt2)]
(5)


(2) 相关熵函数是一个对称函数,Vσ(τ)=Vσ(-τ);
(3) 假设随机过程X和Y满足关系|Xt1-Xt2|>|Yt1-Yt2|,则Vσ(τX) (6) 1.3.1 短码情况 m=1,2,… (7) Vest(m)=E[kσ(d(n)-d(n+m))]= (8) (9) (10) 式中,P表示1倍周期长度L个扩频码元中有P个满足d(n)=d(n+m),另外的L-P个满足d(n)=-d(n+m)。所以,当N/2包含n0(n0≥2)个完整扩频周期时,有 (11) 式中,n1表示N/2个信息码元对应的n0个周期里有n1个信息码取值符号相同,同理n2表示符号相反个数,则满足n1+n2=n0;Q表示N个码元中有Q个满足d(n)=d(n+m)。 当n1≤n2时,有 (12) 当n1>n2时,有 (13) 1.3.2 长码情况 对式(2),若记 由以上理论分析可得出基于相关熵的直扩信号周期估计方法的步骤如下: 步骤1对采样后的信号进行相关熵计算,得到V(m); 步骤3整合得到的两组坐标,根据周期性对这些坐标做进一步修正调整,由相邻两坐标之间间隔即可求得扩频周期。 为了减弱信息码的影响,本文提出延迟相乘相关熵算法。取y(n)与延迟一个码元的y(n+1)相乘得到新的序列y′(n)。m序列具有移位相加性,即m序列和它的移位序列模二相加后所得序列的本原多项式与m序列本原多项式相同,只是初始相位不同。因此,经延时相乘后序列的扩频周期不会改变[12]。而信息码宽远大于扩频码元宽度,故延时相乘后信息码对扩频码的影响可忽略不计。 以短码直扩信号为例,即 y(n)×y(n+1)= (14) 假设噪声与信息码和扩频码均不相关,忽略n=kL(k=1,2,…)对应的少数点,可得 仿真实验扩频码采用m序列,扩频码周期L=63的短码直扩信号,采样速率为扩频码元速率。数据总长N=27L,SNR=-5 dB情况下,在σ取{0.01,0.1,1,5,10,20,50,100}时分别进行300次蒙特卡罗实验。 σ取值对相关熵值的影响可由相关熵定义式分析得到,σ越大,熵值越大;σ越小,熵值越小。图1(a)给出了扩频周期估计结果的相对误差随σ取值变化情况,图1(b)为对应局部放大图。由仿真结果可知σ≥1时都能较准确估计出扩频码周期。 图1 估计结果与σ取值的关系Fig.1 Relationship between the estimation result and the value of σ 图2是在扩频码采用m序列,扩频码周期L=63的短码直扩信号,采样速率为扩频码元速率,σ=10,不加噪声情况下进行300次蒙特卡罗实验的结果。可以看出,在扩频周期的整数倍处相关熵峰值的取值情况与第2节理论分析一致。 图2 不加噪声短码直扩信号的相关熵Fig.2 Correntropy of short-code DSSS signal without noise 图3给出了在与图2对应实验同等条件下,仅有扩频码的相关熵,可以看出不受信息码影响时扩频码相关熵在周期整数倍处有峰值,且峰值均大于非周期整数倍处取值。对比图2、图3及前面的分析可知,信息码的存在使得扩频码相关熵的取值在一定程度上减小了,并使其在扩频码整数倍处的取值出现小于均值(如式(12)所示)和大于均值(如式(13)所示)两种情况。 图3 不加噪声扩频码的相关熵Fig.3 Correntropy of spreading codes without noise 在与图2对应实验同等条件下,对新得到的序列作相关熵,得到结果如图4所示。与图2、图3对比可知,直扩信号经延时相乘处理后能有效消除信息码的影响。同时,峰值间隔没有发生改变,验证了延时相乘处理不会改变扩频周期。 图4 不加噪声直扩信号延迟相乘相关熵Fig.4 Delay-multiplied correntropy of DS/SS without noise 在已有的扩频周期估计方法中,目前最常用的有波动相关法[13]、倒谱估计法[14]和二次谱估计法[15],因此本文用这3种方法作为对比方法。 仿真实验扩频码采用周期L=63的m序列[10],信号分别为短码直扩信号,数据总长N1=27;扩频调制比M2=3的周期长码直扩信号,数据长度N2=81;扩频调制比M3=4.5的非周期长码直扩信号,数据总长N3=162。3种情况均取σ=10,采样速率等于扩频码元速率。不同信噪比下,分别采用相关熵方法、延时相乘相关熵方法和波动相关法估计,做300次蒙特卡罗实验。图5~图7分别为上述短码、周期长码和非周期长码3组实验在不同信噪比下对扩频周期估计的相对误差。 图5 短码直扩信号扩频周期估计Fig.5 PN sequence period estimation of short-code DS/SS signal 图6 周期长码直扩信号扩频周期估计Fig.6 PN sequence period estimation of periodic long-code DS/SS signal 图7 非周期长码直扩信号扩频周期估计Fig.7 PN sequence period estimation of non-periodiclong-code DS/SS signal 短码情况下,如图5所示,对于扩频码周期估计,相关熵法能在SNR=-18 dB时达到97%的估计准确率,延时相乘相关熵法、倒谱估计法和二次谱估计法在信噪比不小于-13 dB 时可达到准确估计,而相关波动法只有在SNR≥-12 dB时估计准确率才能达到90%以上。相关熵法对短码直扩信号扩频周期估计的信噪比容限比倒谱法和二次谱法低3 dB,比波动相关法低6 dB,可见相关熵法的估计性能相对最优,而延时相乘相关熵法估计性能与倒谱和二次谱估计性能相当。 数据长度N=81L的周期长码情况下,如图6所示,相关熵法在SNR≥-13 dB时能达到96%以上估计准确率,二次谱估计法在SNR >-11 dB 时,估计性能不如相关熵法;倒谱法和延时相乘相关熵法信噪比均为-10 dB,波动相关法在SNR≥-10 dB 情况下才能得到准确估计,可以看出在上述实验条件下5种方法的估计效果从信噪比容限角度分析差别不是很大,依然是相关熵法相对最佳,延时相乘相关熵法估计性能不如二次谱法,而较倒谱法和波动相关法好。 数据长度N=162的非周期长码情况,如图7所示,基于相关熵的两种新方法都能在SNR≥-14 dB 时得到准确估计,倒谱估计法和二次谱估计法均可达到-9 dB 的信噪比容限,但波动相关法只有在SNR≥-9 dB 时才能得到准确估计。结果表明在非周期长码直扩情况下,对于估计效果,基于相关熵两种方法明显优于常用的倒谱法、二次谱法和波动相关法。 对比图5~图7可以看出,对于相关熵法和延时相乘相关熵法,在短码直扩信号情况下,前者的估计性能明显优于后者,但在长码情况下,前者并没有显著优势。特别地,延时相乘相关熵法对非周期长码直扩信号扩频周期估计性能较相关熵法好。 针对高斯噪声环境下直接序列扩频信号的扩频周期估计问题,本文首先推导出相关熵隐含的周期性,在此基础上提出了相关熵法。然后分析了直扩信号中信息码序列对扩频周期估计的影响,对此提出一种能消除信息码影响的延迟相乘相关熵估计法。论文通过数值仿真确定了相关熵定义中核长参数σ在扩频周期估计中的最优取值范围。最后,将本文所提出的基于相关熵的两种方法与工程实际常用的倒谱法、二次谱法和波动相关法进行了比较。仿真结果表明基于相关熵的两种方法在短码和长码情况下对扩频周期的估计均有较好的性能。其中,在短码和周期性长码情况下,相关熵法估计性能明显优于其他方法。特别地,对于短码,相关熵法在信噪比低至-18 dB条件下都能准确估计出扩频周期;延时相乘相关熵法估计性能与倒谱估计法相当,虽一定程度增加了计算量,但对于长码,尤其是对非周期长码情况下的扩频周期估计性能优势较为明显。 [1] POLYDOROS A. Autocorrelation techniques for wideband detection of FH/DS waveforms in random tone interference[C]∥Proc.of the IEEE Military Communications Conference, 1983: 781-785. [2] BUREL G. Detection of spread spectrum transmissions using fluctuations of correlation estimators[C]∥Proc.of the IEEE ISPACA, 2000: 5-8. [3] GUAN M X, WANG L. A novel recognition method for low SNR DSSS signals based on four-order cumulant and eigenvalue analysis[J].Chinese Journal of Electronics, 2015,24(3): 650-653. [4] 刘聪峰, 陈鹏举, 王昌宝. 倒谱检测技术研究[C]∥中国电子学会电子对抗分会第十一届学术年会论文集, 2001: 143-146. LIU C F, CHEN P J, WANG C B. Research on the detection technology of the cepstrum[C]∥Proc.of the 11th Annual Conference of the Chinese Society of Electronic Warfare, 2001: 143-146. [5] ZHANG T Q, WU W J, SHI S, et al. The blind periodic estimation of the pseudo noise sequence in multi-rate DS/CDMA transmissions[C]∥Proc.of the Image and Signal Processing, 2014: 24-26. [6] 滕振宇, 耿欣欣, 周帆,等. 基于二次谱的直扩信号伪码周期估计方法研究[J]. 电子技术, 2015, 6(1): 17-20. TENG Z Y, GEN X X, ZHOU F, et al. Research on the periodic estimation method for PN sequence code in DS-SS signal based on the spectrum reprocessing algorithms[J]. Jounal of Electronic Technique, 2015,6(1): 17-20. [7] 王碧雯. 低截获直扩信号检测方法研究[D]. 成都:电子科技大学, 2016. WANG B W. Research on low probability intercept spread spectrum signal detection algorithm[D]. Chengdu: University of Electronic Science and technology, 2016. [8] 资晓军,谢丹,易克初. 基于四阶累积量的二次谱法检测DS-SS伪码周期[J]. 电子信息对抗技术,2006,21(1): 18-21. ZI X J, XIE D, YI K C. The duration estimation of the PN sequence of DS-SS signal based on fourth-order cumulant[J].Jounal of Electronic Information Warfare Technology, 2006, 21(1): 18-21. [9] IGNACIO S, PUSKAL P P, JOSE C P. Generalized correlation function: definition, properties, and application to blind equalization[J]. IEEE Trans.on Signal Processing, 2006, 54(6): 2187-2197. [10] OGUNFUNMI T, PAUL T. The quarternion maximum correntropy algorithm[J].IEEE Journals & Magazines,2015,62(6): 598-602. [11] 金艳,任航,姬红兵.脉冲噪声下及与相关熵的OFDM时域参数估计[J].系统工程与电子技术,2015,37(12):2701-2706. JIN Y, REN H, JI H B. OFDM Time-domain parameters estimation based on correntropy in impulsive noise[J]. Systems Engineering and Electronics, 2015, 37(12): 2701-2706. [12] 刘晓阳. 伪随机序列中本原多项式的研究[D]. 西安: 西安电子科技大学, 2008. LIU X Y. Research on primitive polynomial in pseudo random sequence[D]. Xi’an: Xidian University, 2008. [13] 熊伟杰. 直扩信号盲估计技术研究[D]. 成都: 电子科技大学, 2015. XIONG W J. Research on the technology of DS-CDMA signal blind estimation[D]. Chengdu: University of Electronic Science and Technology, 2015. [14] 王彪, 孙晓雯. 一种有效抑制窄带干扰的水声直扩信号检测方法研究[J]. 科学技术与工程, 2013, 13(7): 1784-1788. WANG B, SUN X W. A effective detection method of underwater acoustic DSSS signals based on narrowband interference suppression[J].Science Technology and Engineering,2013,13(7): 1784-1788. [15] 王绍威, 高勇. 窄带脉冲干扰环境下直扩信号伪码周期及序列的盲估计[J]. 电子信息对抗技术, 2015, 30(4): 8-14. WANG S W, GAO Y. Blind estimation for the pseudo-code sequence and its period of DSSS signals under narrowband impulse interference environment[J]. Electronic Information Warfare Technology, 2015, 30(4): 8-14.1.3 扩频周期估计
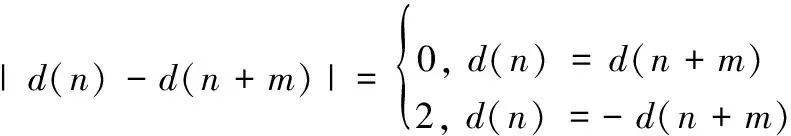



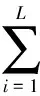


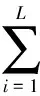
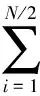

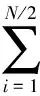

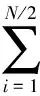




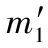
2 延时相乘相关熵法的扩频周期估计
2.1 信息码对相关熵法的影响
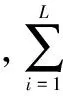
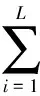

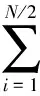
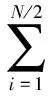
2.2 延迟相乘相关熵
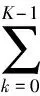
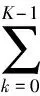
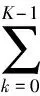

3 仿真实验及分析
3.1 相关熵核长参数σ的选取
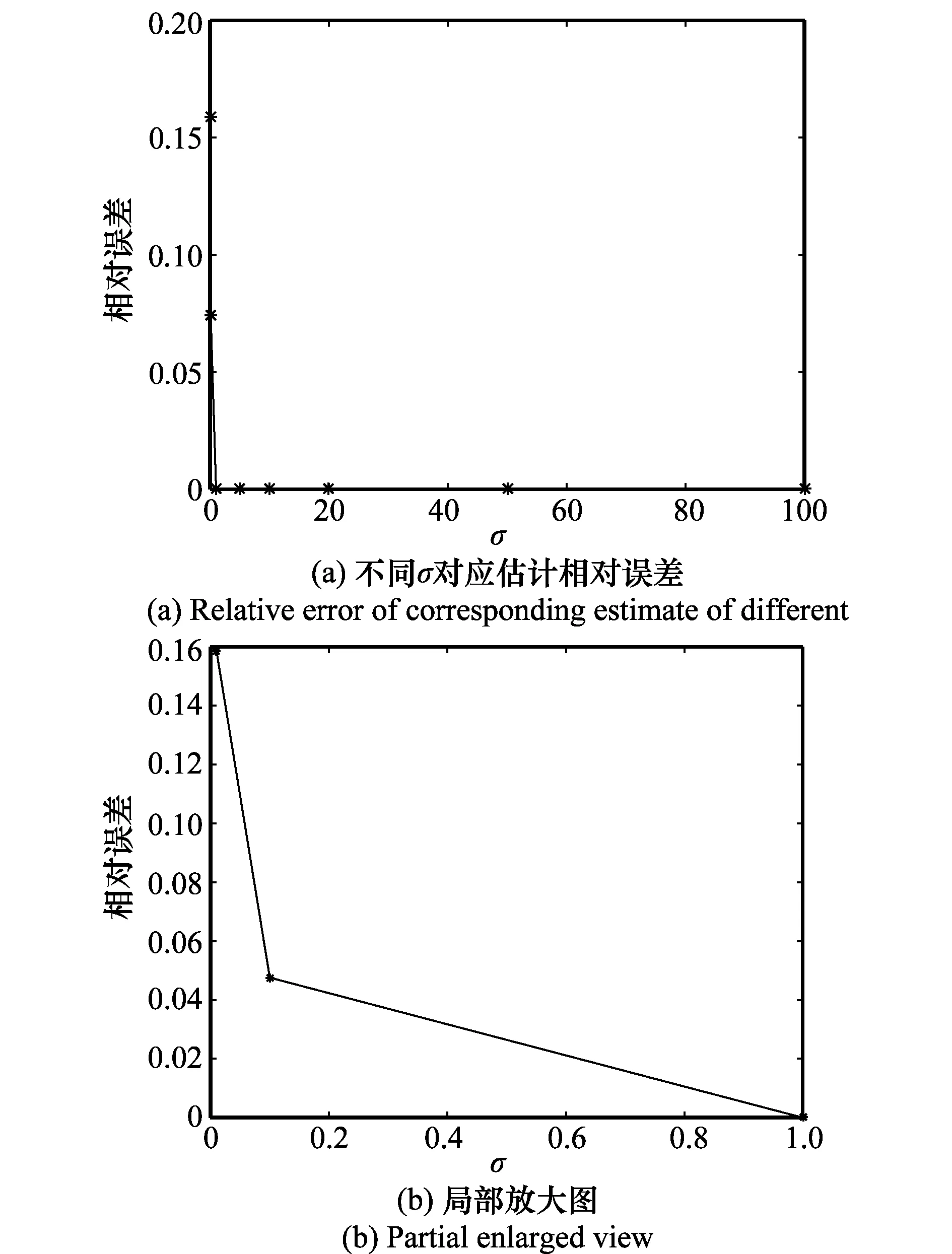
3.2 延时相乘相关熵仿真

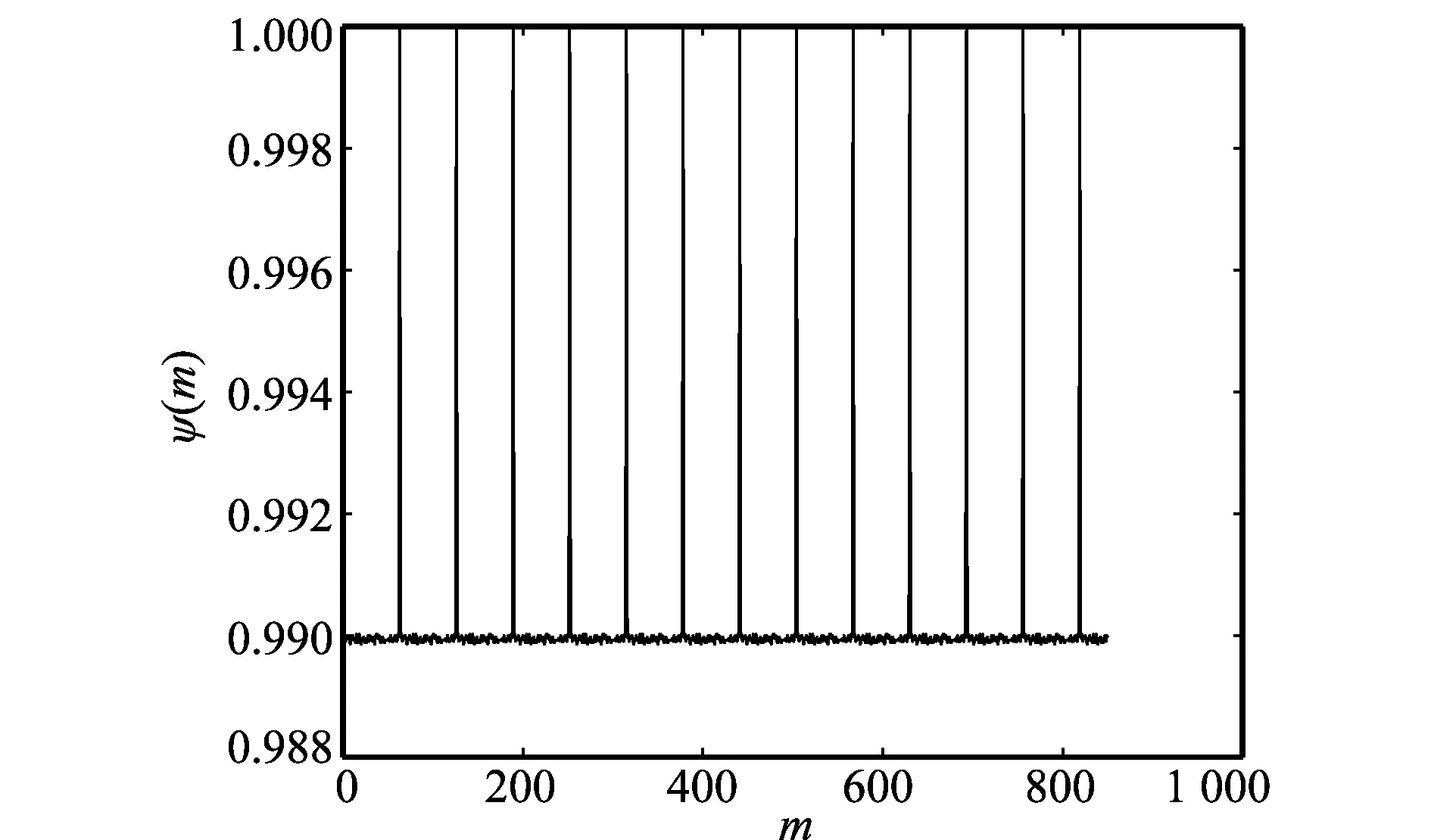

3.3 扩频码周期估计仿真
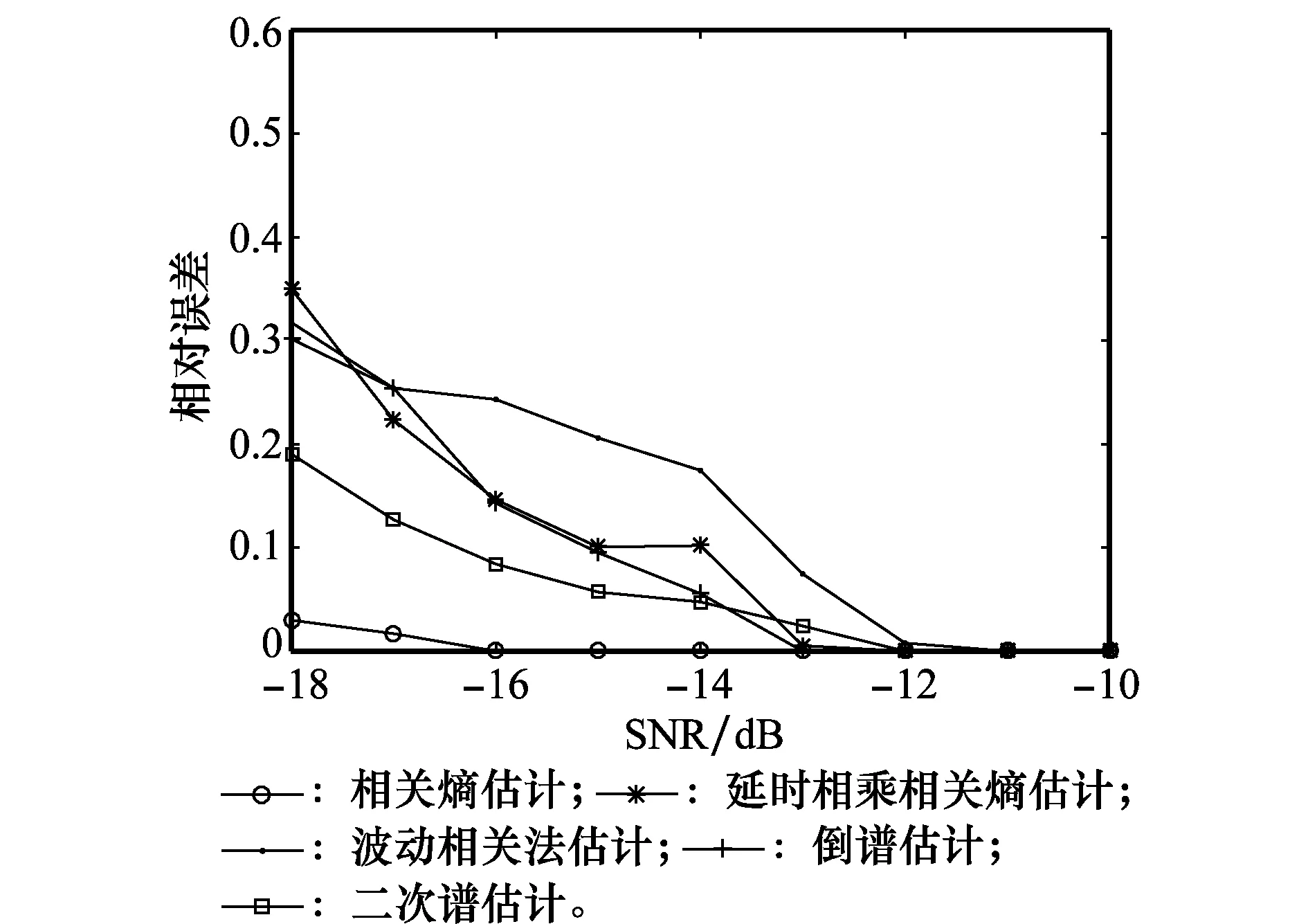
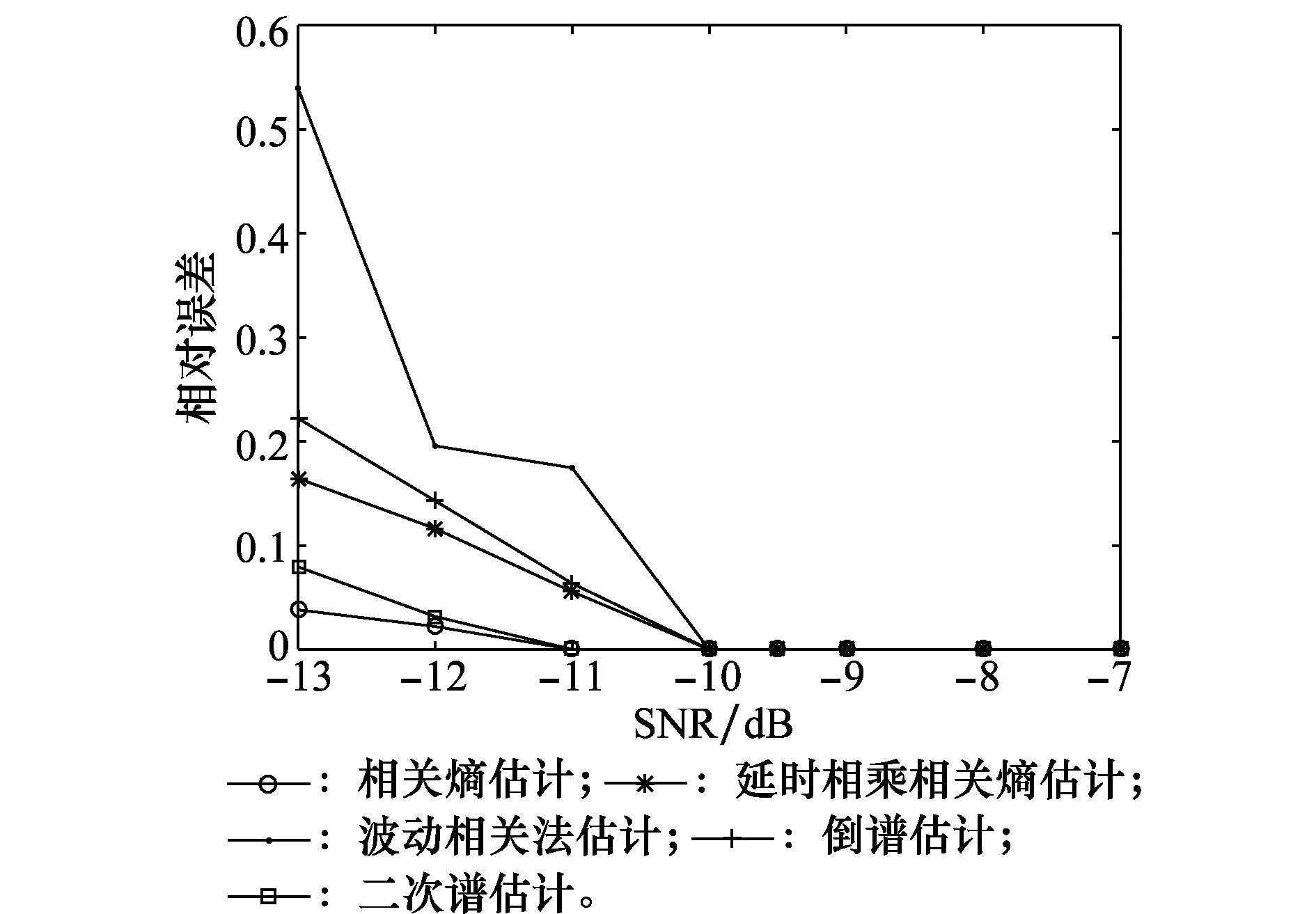
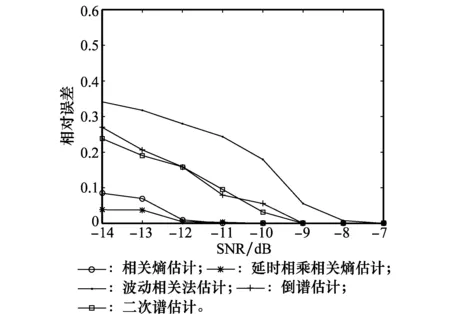
4 结 论
