固定多波束扩频测控信号同步实现技术

丁国栋, 韩月涛, 杨志群

(中国空间技术研究院山东航天电子技术研究所, 山东 烟台 264670)

0 引 言

由于低轨飞行器和地球同步轨道卫星之间的通信距离远,为满足传输速率的要求,收发天线需要具有较高的增益。多波束天线能够高增益地覆盖较大的区域,结合波束切换技术,用户终端跨波束可连续不中断通信,广泛应用于星地、星间数据通信[1-3]。

直接序列扩频(direct sequence spread spectrum, DSSS)由于抗干扰能力强,具有多址能力等优点,在现阶段卫星测控、卫星导航[4-7]方面应用广泛。用户飞行器上的固定多波束测控信号接收机首先需实现跟踪阵列信号的快速同步,然后通过跟踪阵列和切换阵列扫描检测更优波束,保证通信链路的增益最大化,同时保证波束切换过程中连续通信。

由于多普勒效应及收发信机本振不同源,使得接收信号载波与本地载波之间不可避免地存在一定的载波频率偏差及伪码速率偏差。实现相干解调必须获得接收信号伪码定时、码率偏差及载波频率偏差估计值,实现伪码同步和载波同步。文献[8-13]对几种代表性的捕获算法进行研究,解决单个波束扩频信号载波伪码二维捕获问题,通过频率域或者时间域串或并行搜索检测信号相关峰值,获得载波频率偏差、伪码定时和码率偏差估计值。文献[14-19]研究高动态接收机中锁频锁相环(frequency phase locked loop, FPLL)的优化问题和性能分析,并未对多波束信号处理的适应性进行分析。

现有针对固定多波束卫星扩频测控信号同步和波束扫描的研究较少,本文提出一种固定多波束DSSS-二进制相移键控(binary phase shift keying,BPSK)卫星测控信号的快速同步及波束扫描算法,可实现大频偏、低信噪比(signal-to-noise ratio, SNR)条件下快速初始同步、快速波束扫描及波束切换过程中连续通信。

1 问题建模

1.1 固定多波束通信设备组成

固定多波束测控通信设备由固定多波束阵列天线和端机组成。

(1) 固定多波束天线

固定多波束收发一体天线形成跟踪阵列和切换阵列各12个波束覆盖不同空域。发射天线集成功放,实现发射信号的放大。

(2) 端机

端机完成信号的同步、遥控遥测处理、波束扫描、切换控制等。射频通道采用两通道模式,分为跟踪波束阵列和切换波束阵列。经射频接收通道下变频、中频放大后输出两路接收中频信号(跟踪波束和切换波束)到基带模块,基带模块对两路中频采样后在现场可编程门阵列(field programmable gate array,FPGA)中进行基带信号处理及波束扫描选择与控制。

1.2 波束切换选择方法

接收机工作模式有4种,状态转移如图1所示。

图1 状态转换图Fig.1 State transition diagram

(1) 跟踪阵列初始扫描模式

链路尚未建立时,接收机工作在跟踪阵列初始扫描模式(仅码捕获电路工作),对跟踪阵列全部波束进行快速扫描,得到波束功率大小排序。

(2) 跟踪阵列捕获模式

按序依次在较强波束启动码同步、载波同步流程,如果接收机锁定,进入下一工作模式;否则返回上一工作模式。

(3) 跟踪波束解调+切换阵列扫描模式

跟踪阵列保持锁定当前波束,对数据相干解调。基于跟踪波束的载波相位、伪码相位、位定时估计信息辅助,启动切换阵列波束扫描,分时计算信号非相干功率值,比较获得当前最优波束。如果失锁则返回初始扫描模式。

扫描阵列各波束需分时工作:每个阵列扫描时元分为12个波束扫描时帧;每个时帧含8个基本时隙;每个时隙持续时间与符号周期一致。如图2所示,每个时帧的起始时隙作为保护间隔,其余时隙用于计算当前波束信号非相干功率值。

图2 波束扫描时隙设计Fig.2 Timeslot design of beam scanning

假设max(Ej)-Ei>ETh,进入跟踪阵列波束切换模式。其中,i代表当前跟踪阵列的跟踪波束号,j≠i；ETh代表设定的阈值。

(4) 跟踪阵列波束切换模式

切换阵列驻留在更优波束, 接收机同时对跟踪波束和切换阵列波束跟踪。通过相位差估计和补偿实现切换阵列波束快速锁相,并判断是否存在相位模糊。切换过程中保持切换阵列当前波束跟踪,直至跟踪阵列波束切换锁定后,完成本次热切换。

2 同步算法设计

2.1 伪码同步设计

发射端辐射的信号由载波、伪随机噪声(pseudo-random-noise,PRN)码、遥控数据3部分组成。信号采用BPSK调制,载波、伪码、调制数据持续发送。接收端信号用数学公式[6]表达为

r(t)=acos[2π(fn+fd)(t-τ)+φ]·

c(t-τ)d(t-τ)+n(t)

(1)

式中,a表示信号幅度;fn表示标称的信号载波中心频率;fd表示多普勒频率偏差;φ表示载波随机相位差;c(t-τ)表示随机延迟为τ的PRN码;d(t-τ)表示调制数据;n(t)表示白噪声。

接收机对中频信号进行正交下变频处理,得到同相、正交两路基带信号。经相干积分处理[6],以功率衡量的信号检测量表示为

(2)

式中,第1项为信号成分;第2项为滤波后的噪声部分;TC O为相干积分时间;fs为采样率;Rc为PRN码自相关函数;G=fsTC O,且

(3)

(4)

经W次非相干累积之后,得到判决变量为

(5)

进一步可以得到用于判决的统计量为

(6)

(7)

式中,L表示一次搜索码片数。码相位的估计值对应V出现的位置,于是,自适应门限[7]判决可表述为

(8)

式中,V为判决变量;T为根据第1类虚警概率要求预设的恒定常数;U为噪声统计量;H1和H0分别表示信号存在和信号不存在。

图3 码捕获设计框图Fig.3 Code acquisition architecture

所述码捕获算法相干积分时间Tco=L/fc,Tco短于符号周期和伪码周期,因此能忍受的频偏能力相比周期相关[9-10]或全比特积分[11]算法有优势。相比基于FFT的部分匹配滤波器(partial matched filter based FFT,PMF-FFT)算法[12-13],本方法只需一个PMF,降低了实现复杂度。且FFT频偏估计以伪码同步为前提,码同步误差影响更小。

采用改进的非相干延迟锁定环(delay locked loop, DLL)实现码跟踪,利用n路时分复用实现结构,将非相干DLL对初始跟踪码定时误差Δε容忍能力从Δε≤±1/2提高到Δε≤±n/2。即使载波频率偏差、伪码定时和码率偏差造成Δε偏大,在上述范围内仍可正常工作。设计结构框图如图4所示。

图4 多码片DLL结构Fig.4 Multi-chip DLL architecture

非相干DLL由积分器、延迟锁定鉴别器、环路滤波器等组成,采用二阶跟踪环路。鉴相算法采用归一化非相干超前功率减滞后功率的形式,延迟锁定鉴别器的输出为

(9)

式中,ε是t对Tc归一化值;λ是自相关函数峰值。码环误差源主要包括热噪声颤动误差和动态应力误差[6]。非相干前减后功率鉴别器热噪声颤动误差为

σtDLL=

(10)

式中,Bfe为射频前端带宽;码宽Tc=0.325 μs;前后相关器间距D=1;载噪比C/N0=56 dB/Hz;相干积分时间T=15.625 μs;环路滤波器带宽BL=50 Hz时,热噪声颤动误差为0.008 2 chip。

二阶码环在加速度为30g所受的动态应力误差Re表示为

(11)

阻尼因子ζ=0.707时,二阶码环在此动态应力下的稳态跟踪误差Re=0.000 34 chip。码环3σ跟踪误差3σtDLL+Re≤D/4,满足跟踪门限要求。

2.2 载波同步设计

由于初始残余频偏可能超过FPLL牵入范围,需要先进行前向频率估计缩小频率偏差。前向频率捕获算法采用基于FFT的并行频率搜索[9],实现框图如图5所示。

图5 基于FFT的并行频率搜索Fig.5 Parallel frequency search based on FFT

步骤1首先将解扩后持续时间为TPFS的采样数据按Nc点分段累积得到NFFT,S点,且满足TPFS/NFFT,s≪Tb,其中Tb表示比特周期。

步骤2通过复乘消除BPSK调制的影响,避免TPFS>Tb时利用多普勒滤波器组分析信号频谱受调制数据影响的问题。

步骤3对NFFT,S点数据补零后构成NFFT(NFFT=2n)点复数向量,计算NFFT点FFT,可对{-NFFT×fPFS/4,NFFT×fPFS/4}频率区间同时完成搜索,其中,fPFS=1/TPFS。

步骤4NFFT点FFT输出值计算的包络结果可进一步进行NNC次非相干累积。处理输出信号可表示为

k=0,1,…,Nfft-1

(12)

式中,d表示调制数据取值为+1或-1,复乘消除了数据的影响;ej(2π2Δfdt+2Δθ)代表信号频率成分。多比特积分提高了频偏估计精度,通过相干和非相干累积保证检测所需的信噪比(signal-to-noise ratio,SNR)。

载波跟踪采用二阶锁频环辅助三阶锁相环FPLL结构以提高动态应力的跟踪性能[14,16]。跟踪阵列波束切换过程中,需要同时保持两跟踪波束和切换波束载波跟踪,鉴别器和滤波器时分复用输出两路载波数控振荡器(numerically controlled oscillator, NCO)的控制字,设计结构如图6所示。

图6 载波跟踪环路结构Fig.6 Carrier tracking loop architecture

跟踪阵列波束切换模式下,首先以当前跟踪波束的环路输出辅助扫描波束信号跟踪,计算载波相位差;然后将其补偿到扫描波束环路跟踪快速锁定相位,共同跟踪两波束,并判断是否存在相位模糊;最后,切换跟踪波束信号,切换过程不间断输出解调结果,实现热切换。

FPLL环路带宽受载噪比、加加速度、晶振等因素影响,文献[17-19]针对环路参数设计和优化做了大量研究。由于不是本文讨论范围,仅分析本例设计参数的跟踪误差。包括相位抖动和动态应力误差,而造成相位抖动的误差源又主要分为热噪声、机械颤动引起的抖动及艾兰均方差3种。

PLL热噪声均方差σtPLL的估算公式为

(13)

式(13)与环路阶数无关,设计取环路噪声带宽BL=100 Hz,T=31.25 μs,C/N0=56 dBHz时σtPLL=0.93°。

由用户运动和接收装置的机械颤动引起接收机基准振荡频率的抖动,相位抖动方差σv与载波频率、晶振g灵敏度、单边频谱密度积分功率的均方值成正比,与环路带宽成反比,σv约等于2°。艾兰型晶振频率漂移随时间累积引入相位抖动噪声,均方差σA与晶振的h参数、载波频率成正比,与环路带宽成反比[17]。以典型温补晶振指标分析,环路带宽对应σA约等于 2°。

由式(14)计算出PLL相位抖动均方差σi约为3°。

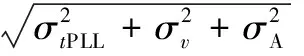
(14)

对于动态应力,三阶PLL可以无稳态误差的跟踪相位斜升信号,动态应力误差主要受加加速度造成。以30g/s的加加速度为例,由式(15),在此动态应力下的稳态跟踪误差θe为0.37°。

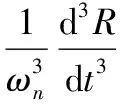
(15)

锁相环3σ跟踪误差3σPLL+θe≤ 45°满足PLL锁定门限要求。

锁频环(frequency locked loop,FLL)热噪声频率抖动均方差σtFLL公式为

(16)

式中,高载噪比F=1;低载噪比F=2[6]。

3σ动态应力误差fe公式为

(17)

以带宽5.2 Hz,波长0.14 m,其他参数同上,计算FLL 3σ跟踪误差3σtFLL+fe=184 Hz,满足FLL锁定要求。

3 仿真与分析

借助Matlab对码捕获算法建模并定点仿真,参数设置为fc=3.069 Mc/s,10阶PRN序列,L=64 chip,ros=2。仿真结果如图7所示。图7仿真比较本方法与PMF-FFT捕获[13]方法检测概率,并分析不同频偏对检测概率影响。仿真表明,码捕获阶段结合串行频率大步进搜索,可使相同检测概率条件下多普勒频偏造成性能损失约1 dB,且相比PMF-FFT捕获所需比特信噪比低1 dB,工程实现复杂度更低。

图7 检测概率比较Fig.7 Comparison of detection probability

按本文所述FPLL设计参数,通过Matlab定点化仿真实际载波跟踪性能。频率跟踪及相位跟踪均方根误差仿真结果如图8所示。仿真结果说明FPLL噪声性能相比PLL差,相位跟踪1σ误差15°对应门限载噪比为54 dBHz,即门限比特信噪比为9 dB。

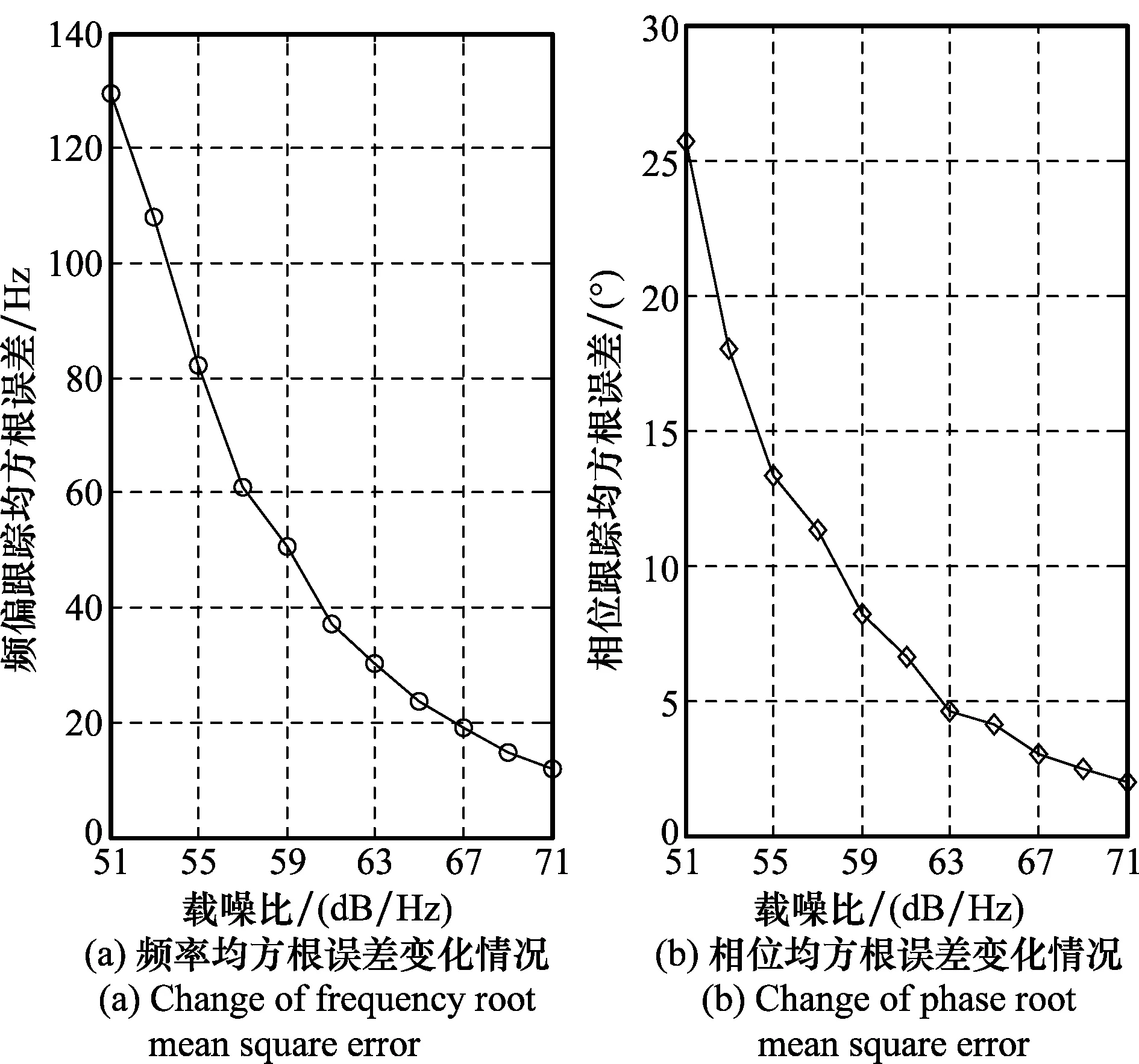
图8 载波同步误差分析Fig.8 Error analysis of carrier synchronization

采用Verilog 语言自顶向下方式描述,使用一片Xilinx公司FPGA(xc5vsx95t)实现本文所述算法,综合后资源占用情况如表1所示。

表1 芯片资源占用率

Modelsim仿真参数如下:Tb=1/32 ms,收发之间的多普勒频偏fd=100 kHz,RPN码速率偏差150 c/s,调制类型及RPN参数同上。跟踪阵列12波束信号样点表示为{rk/2,rk/4,rk-1/4,rk-1/2,rk,rk-2/2,rk-2/4,-rk/2,-rk/4,-rk-2/2,-rk-1/4,-rk-1/2},rk表示式(1)信号对应的中频采样点,通过不同的延迟和幅度差异模拟各波束样点。为简化分析,切换阵列各波束的载波相位与跟踪阵列波束相差角度为δ。

跟踪阵列初始扫描及跟踪波束伪码同步仿真如图9所示。跟踪波束载波同步和扫描阵列扫描仿真如图10所示。跟踪波束热切换仿真如图11所示。

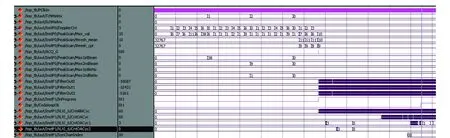
图9 大频偏下初始扫描及码同步仿真Fig.9 Initial scanning and code synchronization under largefrequency offset environment

图10 载波同步及切换阵列扫描仿真Fig.10 Carrier synchronization and switching array scan

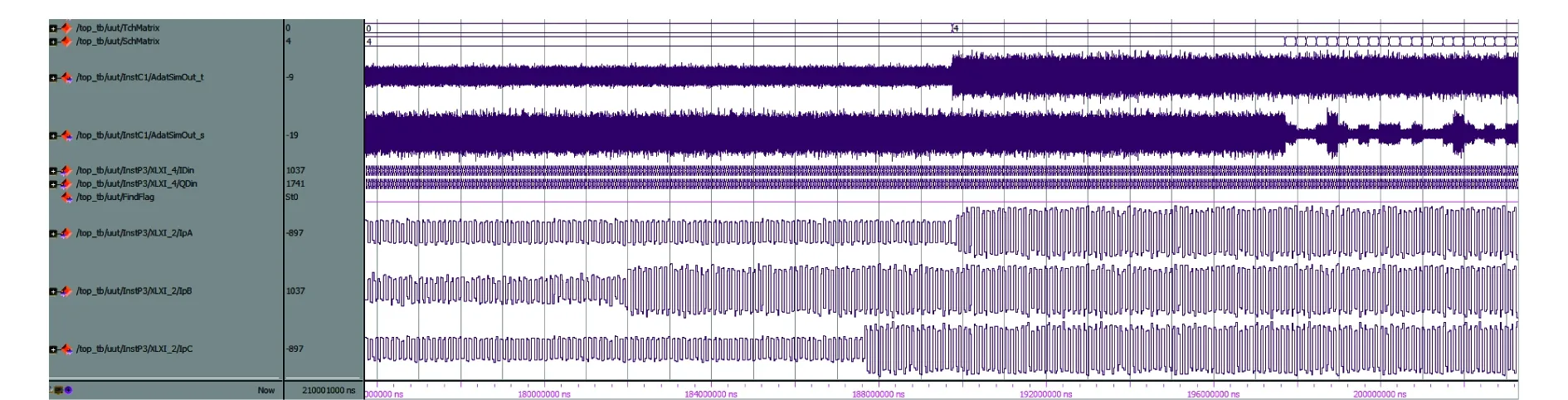
图11 波束切换过程解调仿真Fig.11 Data demodulation during beam switching

图9中设置初始扫描仅扫描前3个波束,因此得到功率最大波束号为0。跟踪阵列(TchMatirx=0)保持波束0启动码同步,当频偏-60 kHz(DopplerCnt=3)时完成码捕获产生ACQ_G脉冲,此时仍有约-40 kHz残余频差;然后3路时分复用DLL启动码跟踪,第0路锁定成功后CodeloopOk标志变为有效,此时FilterOut0输出值计算的码速率估计值约为-149.3 c/s。

图10中FFT峰值164换算为-40.039 kHz,已基本消除频差;后续FPLL跟踪频率和相位变化。载波锁定标志CarrLock有效后,切换阵列开始遍历扫描,AdatSimOut_s波形代表中频信号样点。扫描结束得到符合条件的最优波束,即波束4。

图11中波束切换过程同时对跟踪波束和切换波束解调(同相路基带信号分别见IpA、IpB,IpA和IpB分别代表波束切换和跟踪过程中同时对跟踪波束和切换波束的同相支路信号),以实现波束切换过程中连续解调(IpC的符号作为最终的解调结果，IpC是最终连续输出的同相支路信号，其符号对应调解结果0或1)。本次切换完成后继续下一轮切换阵列扫描。

4 结 论

提出了一种固定多波束扩频测控信号快速同步及波束切换实现方法,简化了载波、伪码、调制数据三维估计问题,并基于Xilinx公司FPGA进行了设计实现和仿真验证。首先,通过部分相关、非相干累积码捕获和多码片DLL获得伪码定时估计和载波频偏粗估计。其次,去调制的FFT前向频率估计完成载波频偏精细估计。最后,FPLL实现持续跟踪解调。时分复用实现形式在不显著增加资源开销情况下大大提高了同步性能,配合完成多波束扫描和切换。验证表明可在大动态、低SNR情况下实现多波束扩频测控信号快速同步、快速切换和连续解调。该方法也可用于突发扩频通信、星间通信、多站测量、卫星导航等领域的接收机同步。

[1] RAO S K.Advanced antenna technologies for satellite communications payloads[J]. IEEE Trans.on Antennas and Propagation, 2015, 63(4): 1205-1217.

[2] TOSO G, MANGENOT P, ANGELETTI P.Recent advances on space multibeam antennas based on a single aperture[C]∥Proc.of the 7th European Conference on Antennas and Propagation, 2013:454-458.

[3] 周乐柱,李斗,郭文嘉. 卫星通信多波束天线综述[J] .电子学报,2001,29(6):824-828.

ZHOU L Z, LI D, GUO W J. Review of multiple beam antennas for satellite communications[J]. Acta Electronica Sinica, 2001, 29 (6): 824-828.

[4] SIMONE L, DE TIBERIS F, BARLETTA F, et al.A X/X spread-spectrum transponder for secure communication[C]∥Proc.of the IEEE Aerospace Conference, 2006:1-11.

[5] EMMANUELE A, ZANIER F, BOCCOLINI G, et al.Spread-spectrum continuous phase modulated signals for satellite navigation[J].IEEE Trans.on Aerospace and Electronic Systems,2012, 48(4): 3234-3249.

[6] KAPLAN E, HEGARTY C. Understanding GPS: principles and applications[M]. Norwood, MA : Artech House,2006.

[7] YEOM S, JUNE Y, LEE S.An adaptive threshold technique for fast PN code acquisition in DS-SS systems[J]. IEEE Trans.on Vehicular Technology, 2011, 60(6): 2870-2875.

[8] DING G D, FANG Z G. An implementation method of partial correlation matched filter in the CDMA receiver[C]∥Proc.of the 2nd IEEE International Conference on Computer and Communications, 2016:2323-2327.

[9] LECLERE J, BOTTERON C, FARINE P, et al.Comparison framework of FPGA-based GNSS signals acquisition architectures[J]. IEEE Trans.on Aerospace and Electronic Systems, 2013, 49(3): 1497-1518.

[10] AKOPIAN D. Fast FFT based GPS satellite acquisition methods[J]. IEE Proceedings-Radar, Sonar and Navigation, 2005, 152(4): 277-286.

[11] 姜冰心,张中兆,孟维晓. 弱信号下软件GPS接收机全比特捕获算法[J].电子技术应用, 2008, 34(9): 99-102.

JIANG B X, ZHANG Z Z, MENG W X.Whole bit acquisition algorithm in software receiver in weak signal environment[J].Application of Electronic Technique, 2008, 34(9):99-102.

[12] LIU C, ZHANG J,ZHU Y B, et al.Analysis and optimization of PMF-FFT acquisition algorithm for high-dynamic GPS[C]∥Proc.of the 5th IEEE International Conference on Cybernetics and Intelligent System, 2011:185-189.

[13] LI Z, LI X,WANG H, et al.A new rapid acquisition and tracking technique for high-dynamic spread spectrum signals[C]∥Proc.of the 8th International Conference on Internet Computing for Science and Engineering, 2015:83-86.

[14] RONCAGLIOLO P A, DEBLASIS C E, MURAVCHIK C H. GPS digital tracking loops design for high dynamic launching vehicles[C]∥Proc.of the 9th IEEE International Symposium on Spread Spectrum Techniques and Applications,2006:41-45.

[15] WON J H, PANY T.Iterative maximum likelihood estimators for high-dynamic GNSS signal tracking[J]. IEEE Trans.on Aerospace and Electronic Systems, 2012, 48(4): 2875-2893.

[16] HUAN H, ZHAO Y M, TAO R, et al.Carrier tracking loop for high-dynamic spread spectrum signals aided by estimation of Doppler rate[C]∥Proc.of the 11th IEEE International Conference on Signal Processing, 2012:1378-1383.

[17] 张提升, 郑建生, 章红平, 等. GNSS接收机晶振参数对载波相位测量的影响分析[J].武汉大学学报信息科学版,2012,37(12): 1413-1416.

ZHANG T S, ZHENG J S, ZHANG H P, et al.Oscillator effects on carrier-phase measurements in GNSS receiver[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1413-1416.

[18] CURRAN J, LACHAPELLE G, MURPHY C.Digital GNSS PLL design conditioned on thermal and oscillator phase noise[J]. IEEE Trans.on Aerospace and Electronic Systems,2012,48(1): 180-195.

[19] JWO D J. Optimisation and sensitivity analysis of GPS receiver tracking loops in dynamic environments[J]. IEE Proceedings-Radar, Sonar and Navigation, 2001, 148(4):241-250.