基于线性调频步进信号的空间自旋目标时变三维成像方法
2018-01-15孙玉雪
孙玉雪, 罗 迎,3, 张 群, 胡 健
(1. 空军工程大学信息与导航学院, 陕西 西安 710077; 2. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071; 3. 信息感知技术协同创新中心, 陕西 西安 710077)
0 引 言
近年来,随着空间碎片、卫星、弹道导弹等空间目标的数量急剧增长,空间环境日益复杂,开展空间目标追踪、测量、分类、识别等对保障我国空间安全、促进国家空间技术发展以及空间和平利用均具有十分重要的意义。
雷达成像技术作为空间监视的重要手段,在目标分类和识别中发挥显著作用。由于空间目标大都具有自旋、进动、翻滚等多种微动形式[1],目标上的每一个散射点在相干积累时间内都会发生距离向和方位向的越距离单元走动,传统的距离-多普勒(range-Doppler, RD)算法难以实现逆合成孔径雷达(inverse synthetic aperture radar, ISAR)像聚焦。文献[2]提出基于Radon-Wigner变换(Radon-Wigner transform, RWT)的成像方法,对解正弦调频RWT结果通过设置阈值提取旋转微动散射点的位置,并对距离-慢时间域目标回波进行频域滤波,从而滤除目标旋转微动回波分量。文献[3]利用经验模式分解(empirical mode decomposition, EMD)将目标自旋部件的回波进行分离,实现对目标主体的聚焦成像。通过ISAR成像技术,能够获得空间目标的形状、径向尺寸、雷达散射截面(radar cross section, RCS)等特征信息[2-4]。相比于二维成像,三维成像技术能够提供更加丰富的目标特征,在获得目标的外形、体积、微动参数等方面具有显著优势。文献[5]利用自旋散射点回波在距离-慢时间域具有正弦包络的特点,在单基雷达条件下提出了基于广义Radon变换-Clean(generalized Radon transform-Clean,GRT-CLEAN)算法的空间自旋目标三维成像方法。但该方法由于受雷达观测视角所限,仅能观测到雷达径向上的微动分量,并不能获得目标实际的空间位置。文献[6]提出了双基雷达条件下的空间自旋目标三维成像方法。文献[7]利用多部雷达获取目标在不同视角下的回波信号,利用多视角观测的一维距离像序列提取进动目标的进动角和真实长度特征。但以上方法在获得目标真实三维成像结果和三维微动特征时,都需要通过对位于不同视角的多部雷达的回波进行联合处理,在实际应用中还面临着雷达同步、目标上散射中心各向异性、遮挡效应等问题,且系统实现较为复杂。为了解决以上空间目标三维成像方法中的问题,文献[8]提出窄带雷达中干涉式三维成像的方法,通过在时频域对不同散射点的回波进行干涉定标,但由于窄带雷达距离向分辨率低,无法获得各散射点在距离向的真实坐标。
目前,在空间目标微动特征提取中,为了能够获得更高的分辨率,宽带雷达已经成为发展趋势[9-11],因此研究宽带雷达中的空间目标三维成像具有重要的现实意义。同时,由于空间目标的轨道高度一般都在数百到数千千米以上,雷达的最大探测距离必须达到该条件才能够实现对空间目标的监视。窄带雷达由于具有较窄的带宽和较小的噪声系数,因此其系统敏感性较高,最大探测距离较远[12]。线性调频步进信号具有较窄的瞬时带宽,但同时又具有较大的合成带宽,可应用于窄带雷达以提高成像质量和降低硬件系统的负担。因此,研究线性调频步进信号体制雷达的空间目标三维成像有着重要的意义。
本文基于线性调频步进信号建立了时变三维成像的信号模型,对距离走动效应进行了详细分析。利用Hough变换将不同散射点在高分辨距离像序列中的自旋轨迹进行了分离。通过干涉处理获得各个散射点在方位向和俯仰向的时变坐标,并通过对高分辨距离像序列的峰值位置进行距离走动校正,获得距离向的时变坐标,进而得到目标散射点的时变三维成像结果。同时,进一步对影响该算法成像精度的因素进行了分析。仿真实验表明,该算法具有较好的鲁棒性。
1 时变三维成像基本原理
三天线三维成像系统如图1所示。3个垂直放置的天线A、B和C组成了地基成像雷达系统。以收发一体天线A为坐标原点构成雷达坐标系XYZ,接收天线B和C分别位于(L,0,0)和(0,0,L)。参考点O在雷达坐标系中的位置为(Xc,Yc,Zc),以O为原点建立目标本地坐标系,各个坐标轴分别平行于雷达坐标系的各坐标轴。目标本地坐标系有着与目标相同的平动速度。空间中一目标以旋转角速度ω绕旋转轴自旋,旋转角速度ω可沿x轴、y轴和z轴分解为角速度矢量(ωx,ωy,ωz)。
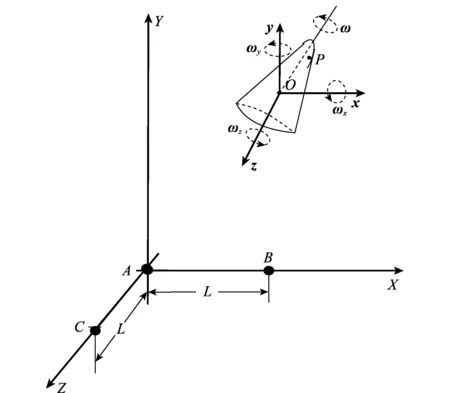
图1 三维成像系统和空间自旋目标几何模型Fig.1 Geometry model of three-dimensional (3-D) imaging system and space rotating target
由图1可知,目标到三天线的距离有差异。由于空间目标距离较远,即相当于处于远场条件,该距离差异很小,一般小于一个距离分辨单元。但该距离差异会反映在三天线回波的相位中,利用干涉处理的方法,提取干涉相位信息,结合空间几何关系,即可恢复出目标散射点的位置坐标。假设目标上一散射点P在目标本地坐标系中的坐标为(x,y,z),天线A和天线B回波的相位历程分别为
φA(t)=ρ·2ΔRA(t)
(1)
φB(t)=ρ·(ΔRA(t)+ΔRB(t))
(2)
式中,ΔRA(t)和ΔRB(t)分别是点P相对于参考点O到天线A和天线B的距离,ΔRA(t)和ΔRB(t)随慢时间t在不断变化。经过干涉处理,即对每一慢时间时刻的相位项作差可得
φB(t)-φA(t)=-ρ(ΔRA(t)-ΔRB(t))=-ρΔRAB(t)
(3)
进一步有
ΔRA(t)-ΔRB(t)=
(RA(t)-ROA(t))-(RB(t)-ROA(t))=
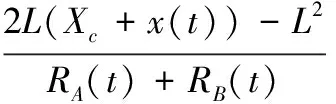
(4)
式中,ROA(t)为参考距离,即点O到天线A的距离。令ΔφAB(t)=φA(t)-φB(t),由于相位项以2π为周期,为避免相位模糊,应保证|ΔφAB(t)|<π[13]。根据式(3)和式(4)可得
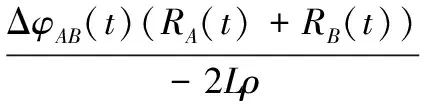
(5)
由式(5),可获得点P在方位向的时变位置。同理,通过对天线A和天线C回波进行干涉处理,可得点P在俯仰向的时变位置为
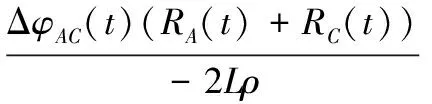
(6)
式中,ΔφAC(t)为天线A和天线C回波相位差;RC(t)为点P到天线C的距离。由此,散射点P在空间中方位向沿x轴和俯仰向沿z轴的时变位置坐标可被重构出来。由于宽带雷达的距离高分辨率,距离向沿y轴的位置可由高分辨距离像序列获得[14]。综合点P在x轴、y轴和z轴的时变坐标即可获得点P的时变三维像。当目标上包含多个散射点时,通过对每一散射点的回波分别进行干涉处理,就可得到目标的时变三维像。
2 信号模型及分析
假设雷达发射线性调频步进信号,每一个脉冲由M个子脉冲组成,步进频率为Δf,子脉冲时宽为τ,子脉冲间隔为T,则天线A接收到的第m个子脉冲回波为
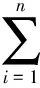
exp(j2π(fc+m·Δf)·(tk-mT-2RiA/c)+jθm)
(7)
式中,e(t)=rect(t/τ)·exp(jπμt2);tk为脉内时间即“快时间”;μ为调频率;θm为第m个子脉冲的初始相位;RiA为第i个散射点到天线A的距离;σi为第i个散射点的散射系数;c为波速;n为散射点个数。参考信号可表示为
E0(tk,m)=e(tk-mT-2ROA/c)·
exp(j2π(fc+m·Δf)·(tk-mT-2ROA/c)+jθm)
(8)
对子脉冲进行“dechirp”处理,结果为
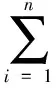
(9)
式中,t′=tk-mT-2ROA/c;ΔRiA=RiA-ROA。关于t′做傅里叶变换并去除“残余视频相位项”和回波包络“斜置”项,式(9)变为
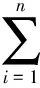
(10)
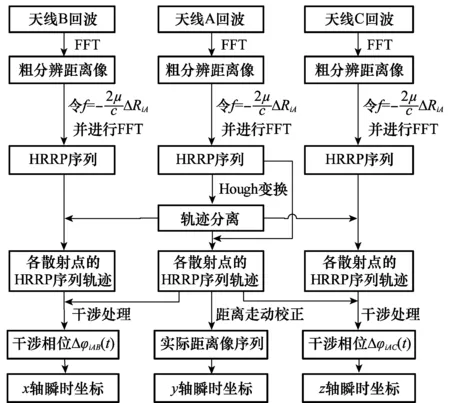
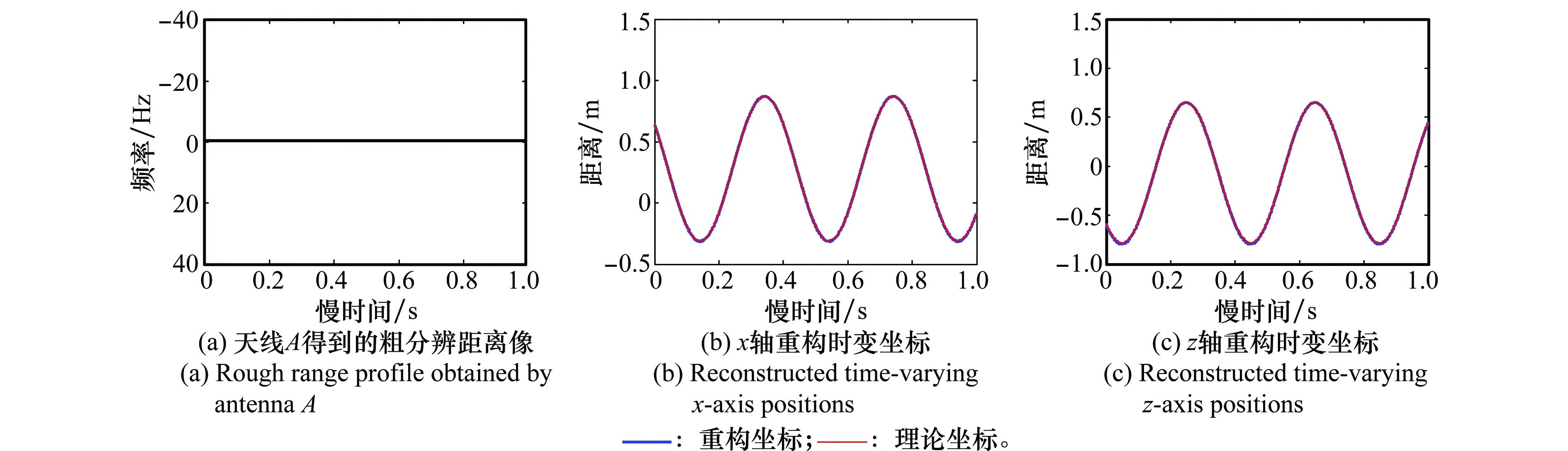
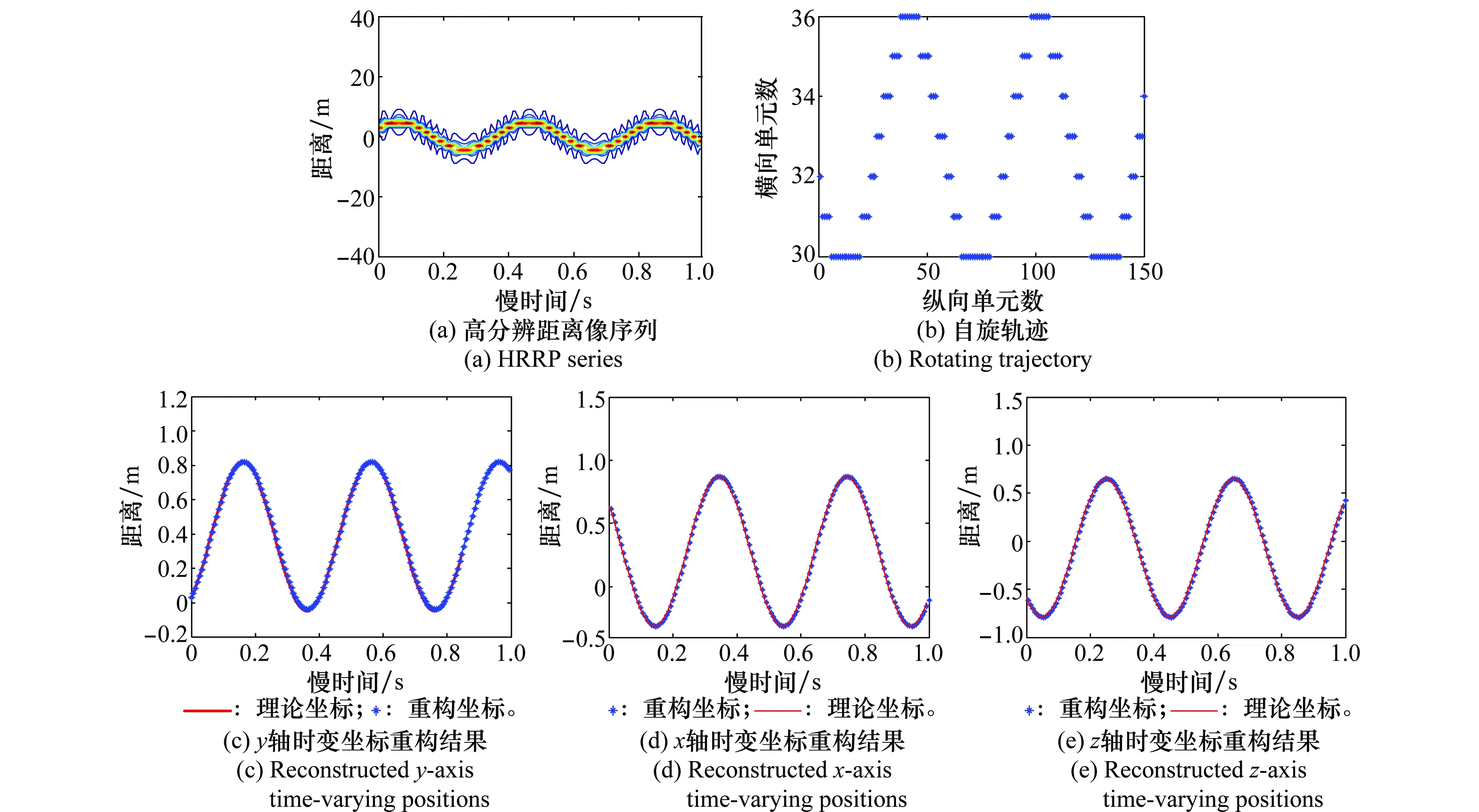
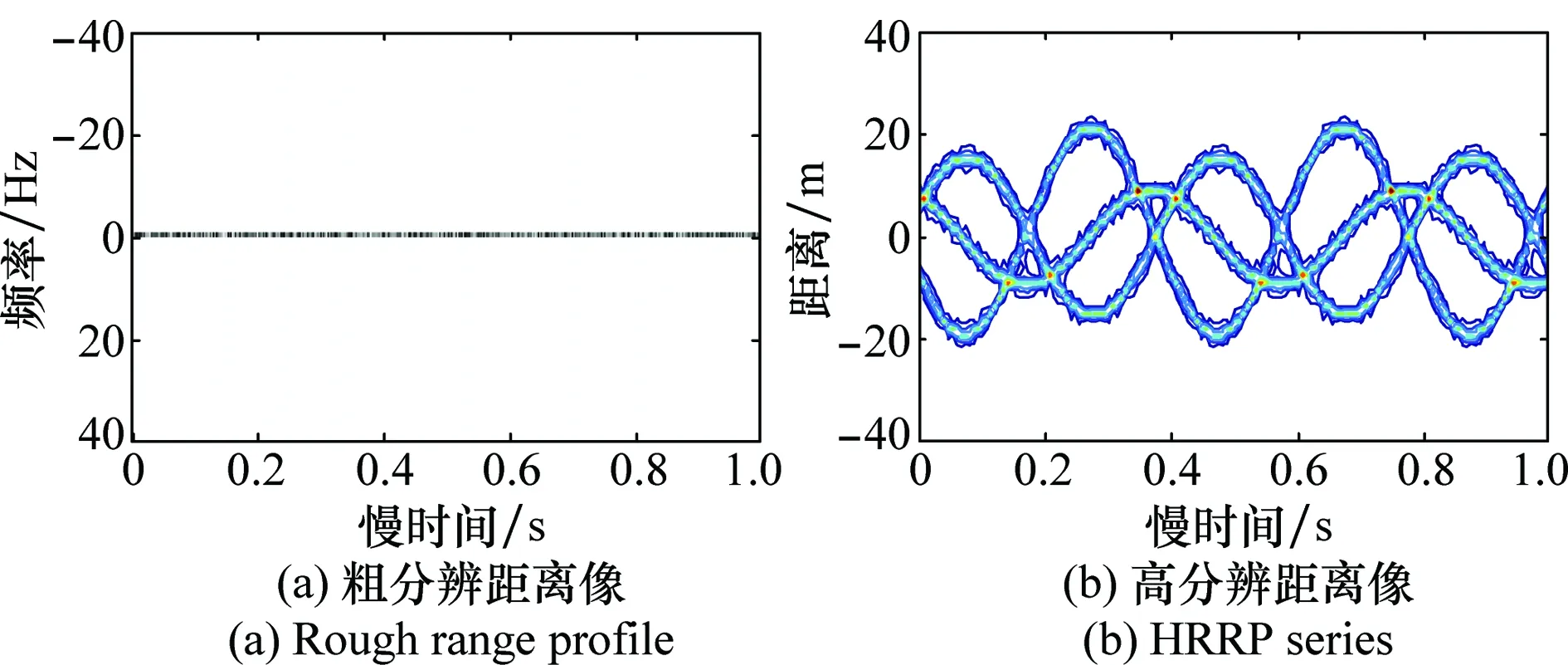
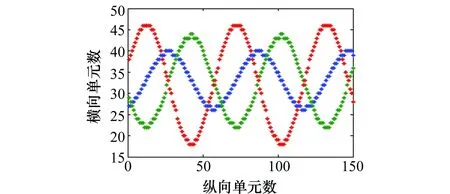
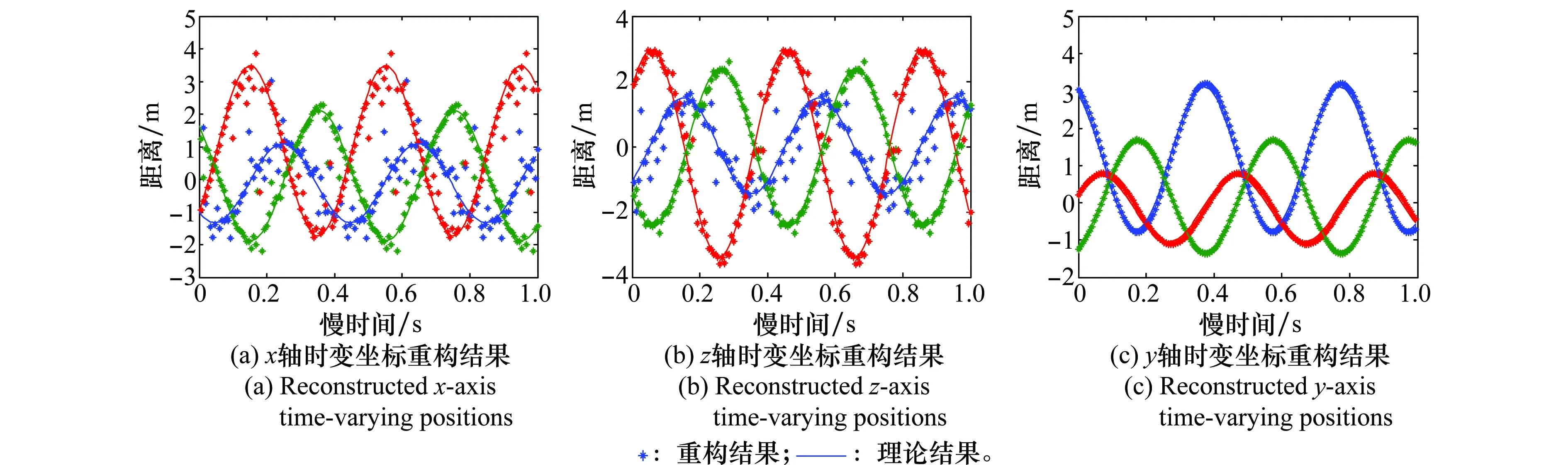
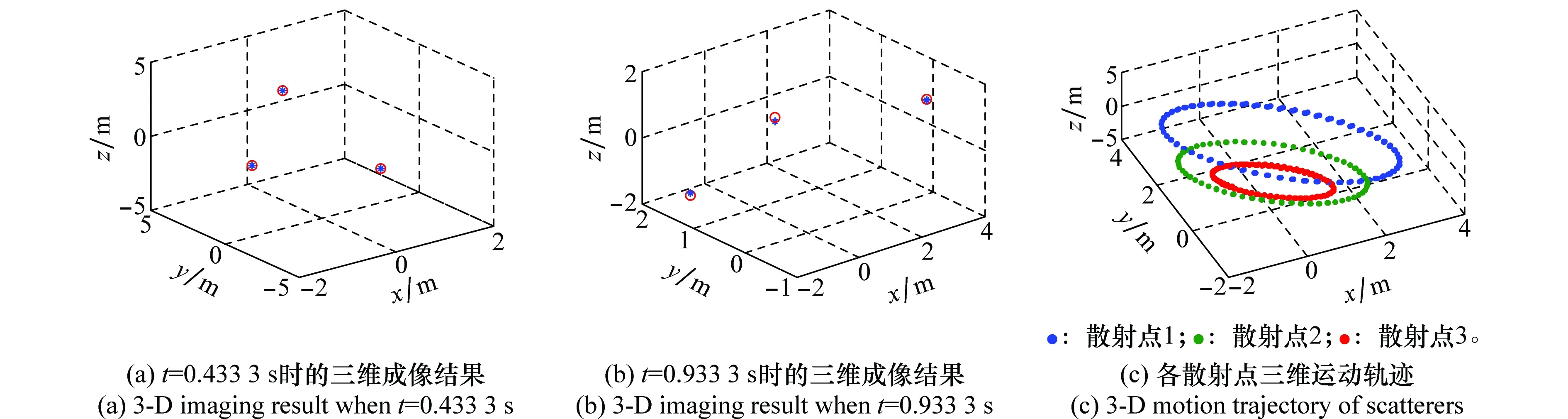
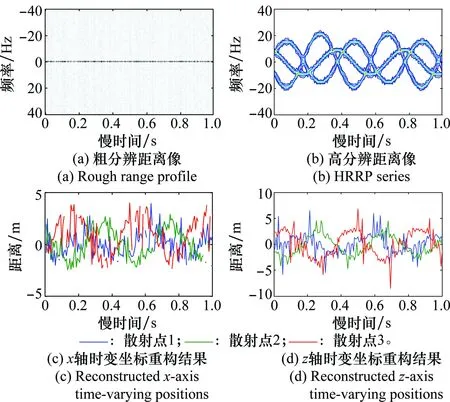
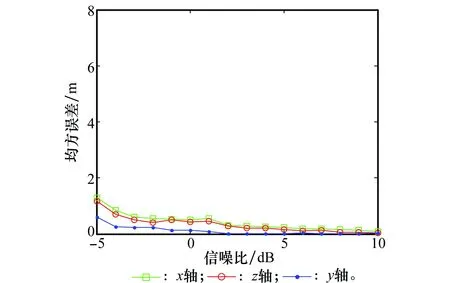
式(10)即为“粗分辨距离像”,假设目标平动已被精确补偿[15],则ΔRiA表示相对自旋运动距离。对于空间中尺寸较小的目标,自旋运动距离总是小于粗距离分辨单元的长度,即|ΔRiA| ΔR0iA(t)=RbA+ρiAcos(Ωt+φiA) (11) 式中,RbA为旋转中心到参考点的距离;Ω为旋转角速度;ρi和φi分别为第i个散射点的旋转半径和初始相位。由式(11)可得散射点在天线A视线方向的旋转速度为 viA(t)=-ρiAΩsin(Ωt+φiA) (12) 在一个脉冲持续时间内,第i个散射点的旋转速度viA近似不变,由于旋转散射点在脉冲串内同样产生位移,即脉冲串内距离走动,因此,第i个散射点在天线A视线方向的位移可重写为 ΔRiA(t,m)=ΔR0iA(t)+viA(t)mT (13) 抽取式(10)中的“粗分辨距离像”所在的行信号,即令f=-2μΔRiA/c,将式(12)和式(13)代入并做关于m的傅里叶变换可得 (14) 此即散射点的高分辨距离像序列,可见其峰值位于 (15) 式(15)通过两边同除以-2Δf/c可实现距离像定标,但由于脉内距离走动导致产生附加项,即式(15)中的第2项和第3项,第2项导致距离像走动,而第3项使距离像展宽。但从式(14)中可以看到,虽然高分辨距离像产生了走动以及展宽,但相位项并未受影响。因此,在后续进行干涉处理时可直接对相位项进行提取,无需考虑脉冲串内距离走动的影响。 采取与天线A回波相同的处理,可得到由天线B获得的高分辨距离像序列为 (16) 为了后续能够对目标散射点时变三维成像结果进行优化,在进行干涉处理之前需要对各个散射点在高分辨距离像序列中的自旋轨迹进行分离,即找出各个散射点在每一慢时间时刻的高分辨距离像峰值位置。由式(15)可知,尽管自旋散射点的高分辨距离像序列发生了走动,但仍然表现为正弦曲线的形式,如果能够将各条正弦曲线的参数提取出来,利用得到的正弦曲线就可以反映出散射点的自旋轨迹。Hough变换最早应用于图像边缘检测,用于检测直线和满足特定解析式的各类曲线[16],后被用于SAR/ISAR成像领域以进行目标识别[17-18]以及被用来进行目标微动特征提取[19]。本文采用Hough变换来提取高分辨距离像序列中的正弦曲线参数,从而获得各散射点的自旋轨迹。Hough变换方程可构造为 (17) 将获得的各条正弦曲线以慢时间采样间隔进行离散化处理,并将各离散值对应到高分辨距离像的距离分辨单元中,进而得到各个散射点在高分辨距离像序列中的自旋轨迹。 在获得各个散射点在高分辨距离像序列中的自旋轨迹的基础上,对每一散射点的高分辨距离像序列在各个干涉平面内分别进行干涉处理。假设第i个散射点由天线A、天线B和天线C获得的高分辨距离像序列分别为EAi(t,fm),EBi(t,fm)和ECi(t,fm)。对其进行干涉处理,可表示为 (18) (19) 式中,angle表示取复数的相角;上标“*”表示共轭运算。结合式(3)以及式(5)、式(6),即可获得各散射点在x轴和z轴的时变位置。 y轴的位置可由高分辨距离像序列来获得,但由于距离走动和展宽的影响,高分辨距离像序列不能直接反应目标散射点的距离向信息,需进行校正处理。由于三天线结构与目标距离之间的远场条件,散射点到三天线的距离差异一般小于一个精距离分辨单元的长度,因此三幅高分辨距离像序列反应的目标散射点的径向距离信息基本相同,可根据任意一幅高分辨距离像序列来重构y轴的时变位置,在此采用天线A获得的高分辨距离像序列。根据式(15),由于距离展宽项要远小于前两项,在确定高分辨距离像峰值位置时可将其忽略,将式(11)和式(12)代入并经距离定标后可得 cos(Ωt+φiA+φa) (20) 式中 式(20)即为产生距离走动的高分辨距离像序列峰值,与式(11)未发生距离走动的理论值相比,可见其幅度与相位均发生了改变,该结论在文献[18]中也得到证明。因此,目标散射点的实际距离向位置应表示为 (21) 散射点到雷达天线的距离和散射点y轴坐标之间满足2(yi(t)+Yc)≈RiA(t)+RiB(t),结合式(18)和式(19),式(5)和式(6)可以重写为 (22) (23) 根据各个散射点的空间三维坐标{xi(t),yi(t),zi(t)},i=1,2,…,n,就可重构出目标的时变三维像。完整的时变三维成像流程图如图2所示。图2中,HRRP表示高分辨距离像(high resolation range profile, HRRP);FFT表示快速傅里叶变换(fast Fourier transform, FFT)。 图2 时变三维成像流程Fig.2 Flow chart of time-varying 3-D imaging 目标的y轴坐标由于是通过高分辨距离像序列获得的,因此与高分辨距离像的分辨率以及信噪比有关。线性调频步进信号的合成带宽越大的情况下,距离分辨率就越高;而噪声过大的情况下,高分辨距离像被噪声淹没,Hough变换无法提取参数。x轴和z轴坐标是通过干涉处理得到的,二者处理过程完全相同,以x轴重构坐标为例进行分析。由式(22)可知,第i个散射点的x轴重构坐标是一个多变量函数,即 x(t)=f(Δφ(t),y(t),L,(Xc,Yc)) (24) x(t)的均方误差(mean square error, MSE)为 (25) 式中,σΔφ(t),σy(t),σL和σ(Xc,Yc)分别为Δφ(t),y(t),L,(Xc,Yc)的测量均方根误差(root mean square error,RMSE)。根据式(22)可得 (26) 由式(25)和式(26)分析可得以下结论:①式(25)右边的第4项与雷达测距精度有关,主要由距离探测设备的性能以及距离生成算法决定;②由式(26)可知,在测量RMSE一定的条件下,天线之间的距离L越大,x(t)的MSE就越小,但是L不可能无限增大,实际当中,当L过大时会造成三天线观测视角的差异,进而带来同步、散射中心各向异性等问题,并且当L增大到一定程度时,会引起干涉相位模糊,因此L的选择应视具体情况而定;③y轴坐标重构值的精度会对x轴的重构产生一定影响;④相位测量误差σΔφ(t)主要由噪声、距离旁瓣和高分辨距离像序列交叉引起。噪声直接叠加在干涉相位上,使得干涉相位失真,从而获得的x轴坐标偏离真实值,因此当信噪比过低的情况下,该算法不再适用;当目标上包含多个散射点时,某一散射点的高分辨距离像的主瓣必然会受到其他散射点距离旁瓣的影响,从而使主瓣的干涉相位产生一定偏差;高分辨距离像序列交叉是指两个或多个散射点的高分辨距离像在某一慢时间时刻落在同一个距离分辨单元中,即在高分辨距离像序列中有交叉点,因此该距离分辨单元中的回波相位为多个散射点的相位非线性叠加,导致相位失真,当用于进行干涉处理获取散射点坐标时,会产生坏值。 为验证算法有效性,首先建立单散射点目标模型。参考点在雷达坐标系中的位置为(0 km,500 km,0 km),一散射点在目标本地坐标系中的位置为(0.64 m,0.03 m,-0.59 m)。天线的基线长度L=100 m。雷达合成总带宽Bs=100 MHz,载频fc=10 GHz,距离分辨率Rresolution=1.5 m,脉冲重复频率为150 MHz。一个脉冲串内的子脉冲数M=64,步进频Δf=1.562 5 MHz,子脉冲时宽τ=9.765 6 μs,成像时间为1 s。单散射点模型中不需对散射点的自旋轨迹进行分离,可从粗分辨距离像中直接提取干涉相位信息。粗分辨距离像如图3(a)所示,取每一脉冲串中的第一个子脉冲对应的散射点所在距离单元,通过干涉处理获得的x轴和z轴时变坐标分别如图3(b)和图3(c)所示。通过与理论值的对比可见,由粗分辨距离像中相位的干涉结果能够精确地逼近目标散射点实际的位置坐标,重构的x轴和z轴坐标的MSE分别为8.276 1 μm和2.165 6 μm。 图3 粗分辨距离像和干涉处理结果Fig.3 Rough range profile and interferometric processing result 根据获得的粗分辨距离像合成高分辨距离像,结果如图4(a)所示。可以看出,高分辨距离像发生了一定的展宽效应。利用Hough变换提取高分辨距离像序列中的曲线参数,结果如表1所示,并将其离散化之后对应到高分辨距离单元中形成散射点自旋轨迹如图4(b)所示。沿着得到的自旋轨迹方向,进行干涉处理,可分别得到x轴和z轴时变坐标如图4(d)和图4(e)所示,其MSE分别为0.497 21 mm和0.703 26 mm。由此可见,高分辨距离像的展宽效应导致峰值点处的能量也会发生散焦,与粗分辨距离像相比,干涉结果受到了一定影响,但是仍然处于较为精确的范围之内,证明了本文所提算法的有效性。根据式(21),对Hough变换得到的高分辨距离像峰值位置进行校正后得到y轴时变坐标,如图4(c)所示,其MSE为0.151 52 mm。 表1 Hough变换提取的散射点参数 图4 由高分辨距离像序列重构坐标结果Fig.4 Reconstructed results by HRRP series 当目标上包含多个散射点时,距离旁瓣和高分辨距离像序列交叉都会对干涉结果产生一定影响。本节验证在多散射点条件下算法的有效性。假设目标模型中包含3个散射点。旋转频率均为2.5 Hz,旋转半径为(0.95 m,1.52 m,1.99 m),散射系数均为1,其他参数与第4.1节相同。经过处理得到的粗分辨距离像以及高分辨距离像序列分别如图5(a)和图5(b)所示。经过Hough变换提取高分辨距离像序列中的曲线参数,结果如表2所示。将提取到的曲线离散化并对应到距离分辨单元中,得到的各个散射点在高分辨距离像序列中的自旋轨迹如图6所示。 图5 回波处理结果Fig.5 Processing results of echo 参数RbCΩθ点11.20102.50.39点20.16162.5-1.18点3-0.16212.51.96 图6 自旋轨迹分离结果Fig.6 Rotating trajectory separation result 利用得到的各个散射点在高分辨距离像序列中的自旋轨迹,分别对天线A、天线B和天线A、天线C得到的高分辨距离像序列中的每一散射点沿轨迹方向分别进行干涉处理,天线A、天线B组成的干涉平面可获得x轴时变坐标,天线A、天线C组成的干涉平面可获得z轴时变坐标。由于高分辨距离像序列交叉的影响,在有交叉的时刻会出现重构坐标严重偏离坐标轨迹的情况,即出现坏值,需根据重构结果聚集的区域范围设置阈值,剔除坏值。在这里设置x轴重构结果阈值为[-2.5 m,4.5 m],z轴重构结果阈值为[-4 m,3 m],获得的结果分别如图7(a)和图7(b)所示,图中不同颜色分别代表不同的散射点的坐标。从图7(a)和图7(b)可以看出,由于距离旁瓣的影响,以及存在未被剔除的交叉点重构结果,重构坐标中某些时刻的位置出现在理论值附近波动的情况。根据Hough变换提取到的正弦曲线参数,可得到每一散射点的精分辨距离像序列峰值的具体数值,根据式(21)对其距离走动引起的幅度和相位变化进行校正处理,得到每一散射点y轴的时变坐标,重构结果如图7(c)所示。为了进一步优化坐标重构结果,对x轴和z轴重构坐标 进行拟合,得到平滑的时变坐标轨迹。拟合之后散射点的x轴和z轴以及y轴坐标值的MSE如表3所示。可见,重构坐标精确地逼近理论值。经过拟合之后,即可获得散射点目标的时变三维成像结果,图8(a)和8(b)分别是选取了t=0.433 3 s和t=0.933 3 s的三维成像结果。在成像时间内各个散射点的三维运动轨迹如图8(c)所示。 表3 重构结果均方误差 图7 散射点三维时变坐标重构结果Fig.7 Reconstructed time-varying 3-D positions results of scatterers 图8 散射点目标时变三维成像结果Fig.8 Time-varying 3-D imaging results of scatterers 由于回波干涉相位会受到噪声的影响,从而影响散射点坐标重构。为验证该算法在噪声环境下的性能,对第4.2节中的信号模型加入高斯白噪声,散射点模型及其他参数不变。由于高分辨距离像序列是经过两次傅里叶变换得到的,具有较好的抗噪性。当信噪比为5 dB时,如图9(b)所示,高分辨距离像受噪声影响很小,因此在利用Hough变换提取参数时,仍具有良好的鲁棒性,y轴坐标重构结果精确度不受影响。但噪声对干涉相位影响较大,x轴和z轴重构坐标发生明显波动,如图9(c)和图9(d)所示。采用拟合将x轴和z轴重构坐标平滑之后,得到三维重构坐标的MSE如表4所示。 表4 重构结果均方误差(5 dB) 可以看出,在5 dB的噪声条件下,该算法仍然能够较为准确地获得目标散射点的三维坐标信息。在不同信噪比条件下进行了17次蒙特卡罗仿真实验,散射点重构三维坐标的MSE随信噪比的变化情况如图10所示。由图10可以看出,随着信噪比的降低,各维坐标重构误差逐渐增大,在信噪比低于2 dB时,三维坐标的重构误差均明显增大,在信噪比高于2 dB时,重构误差基本较低。对于空间环境而言,噪声一般处于较低水平,因此该算法可适用于对空间目标进行三维成像。 图9 SNR=5 dB时的距离像以及干涉处理结果Fig.9 Range profile and interferometric result when SNR=5 dB 图10 不同信噪比下的成像误差Fig.10 MSEs with different SNRs 将干涉技术与微多普勒效应相结合,提出了一种基于线性调频步进信号的空间自旋目标时变三维成像方法。首先建立了时变三维成像的信号模型,并详细分析了基于线性调频步进信号的高分辨距离像序列走动效应。然后利用Hough变换提取高分辨距离像序列中各个散射点自旋轨迹的曲线参数,获得了其自旋轨迹。最后通过对每个散射点的高分辨距离像序列在不同干涉平面内沿自旋轨迹方向进行干涉处理,分别得到了时变的方位向和俯仰向坐标,距离像的坐标通过对高分辨距离像序列的距离走动效应进行校正之后可获得,从而实现了对散射点目标的时变三维成像。同时,还对时变三维成像精度的影响因素进行了分析,仿真实验验证了所提方法的有效性和鲁棒性。该方法能够利用一部多天线雷达实现对空间自旋目标的时变真实三维成像,为空间目标三维成像以及三维微动特征提取提供了新的思路。 [1] CHEN V C, LI F Y, HO S S, et al. Micro-Doppler effect in radar: phenomenon, model and simulation study[J]. IEEE Trans.on Aerospace and Electronic System, 2006, 42(1): 2-21. [2] 吴亮,黎湘,魏玺章,等. 基于RWT的旋转微动目标二维ISAR成像算法[J].电子学报,2011,39(6):1302-1308. WU L, LI X, WEI X Z, et al. 2D ISAR imaging algorithm for rotating micro-motion target based on RWT[J]. Acta Electronica Sinica, 2011,39(6):1302-1308. [3] BAI X R, XING M D, ZHOU F, et al. Imaging of micromotion targets with rotating parts based on empirical-mode decomposition[J]. IEEE Trans.on Geoscience and Remote Sensing, 2008, 46(11): 3514-3523. [4] BAI X R, ZHOU F, BAO Z. High-resolution three-dimensional imaging of space targets in micro-motion[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(7): 3428-3440. [5] WANG Q, XING M D, LU G Y, et al. High-resolution three-dimensional radar imaging for rapidly spinning targets[J]. IEEE Trans.on Geoscience and Remote Sensing,2008,46(1):22-30. [6] BAI X R, XING M D, ZHOU F, et al. Scaling the 3-D image of spinning space debris via bistatic inverse synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Letter,2010,7(3):430-434. [7] 艾小锋,李永祯,赵锋,等. 基于多视角一维距离像序列的进动目标特征提取[J]. 电子与信息学报, 2011, 33(12): 2846-2851. AI X F, LI Y Z, ZHAO F, et al. Feature extraction of precession targets using multi-aspect observed HRRP sequences[J]. Journal of Electronics and Information Technology,2011,33(12): 2846-2851. [8] 陈永安,罗迎,张群,等.基于多天线干涉处理的窄带雷达空间旋转目标三维成像[J].空军工程大学学报(自然科学版),2016,17(4): 46-51. CHEN Y A, LUO Y, ZHANG Q, et al. Three dimensional imaging of spinning space target based on multi-antenna interferometric processing[J]. Journal of Air Force Engineering University (Natural Science Edition), 2016, 17(4): 46-51. [9] CAMP W W, MAYHAN J T, O’DONNELL R M. Wideband radar for ballistic missile defense and range-Doppler imaging of satellites[J].Lincoln Laboratory Journal,2000,13(2):267-280. [10] ROTH K R, AUSTIN M E, FREDIANI D J, et al. The Kiernan reentry measurements system on Kwajalein atoll[J]. Lincoln Laboratory Journal, 1989, 2(2): 247-276. [11] AIDA S, PATZELT T, LEUSHACKE L, et al. Monitoring and mitigation of close proximities in low earth orbit[C]∥Proc.of the 21st International Symposium on Space Flight Dynamics, 2009. [12] 徐丹雷,杜兰,刘宏伟,等.基于复数因子分析模型的步进频数据压缩感知[J]. 电子与信息学报, 2015, 37(2):315-321. XU D L, DU L, LIU H W, et al. Compressive sensing using complex factor analysis for stepped-frequency data[J]. Journal of Electronics and Information Technology,2015,37(2):315-321. [13] 张冬晨, 王东进, 陈卫东. 基于联合互时频分布的InISAR三维成像方法[J]. 电子学报, 2009, 37(4): 833-838. ZHANG D C, WANG D J, CHEN W D. An InISAR imaging method based on joint cross-time-frequency distribution[J]. Acta Electronica Sinica, 2009, 37(4): 833-838. [14] 孙玉雪, 罗迎, 张群, 等. 空间自旋目标宽带雷达干涉三维成像方法[J]. 航空学报,2017,38(4): 227-239. SUN Y X, LUO Y, ZHANG Q, et al. Interferometric 3-D imaging for space rotating targets in wideband radar[J]. Acta Aeronautica et Astronautica Sinica, 2017,38(4): 227-239. [15] ZHAO Y Q, WANG G Z, BAI Y Q, et al. A new method of translational compensation for space spinning target based on EMD[C]∥Proc.of the IEEE International Conference on Signal Processing, 2013: 1-5. [16] DEANS S R. Hough transform from the radon transform[J].IEEE Trans.on Pattern Analysis and Machine Intelligence, 1981, 3(2): 185-188. [17] GUO K Y, HOARE E G, IASTEH D, et al. Road edge recognition using the stripe Hough transform from millimeter-wave radar images[J]. IEEE Trans.on Intelligent Transportation Systems,2015,16(2):825-833. [18] 刘剑, 赵艳丽, 罗鹏飞. 基于Hough变换的低可观测海面运动目标检测[J]. 系统工程与电子技术, 2004, 26(3):393-395. LIU J, ZHAO Y L, LUO P F. Detection of lowlying sea surface moving target via Hough transform[J]. Systems Engineering and Electronics, 2004, 26(3):393-395. [19] 罗迎,张群,柏又青,等.线性调频步进信号雷达微多普勒效应分析及目标特征提取[J].电子学报,2009,37(12):2741-2746. LUO Y, ZHANG Q, BAI Y Q, et al. Analysis of micro-Doppler effect and feature extraction of target in frequency-stepped chirp signal radar[J]. Acta Electronica Sinica, 2009, 37(12): 2741-2746.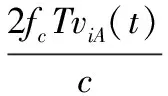
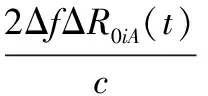
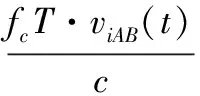
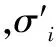
3 时变三维成像
3.1 散射点自旋轨迹分离
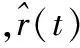
3.2 空间三维坐标重构
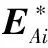
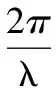
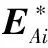
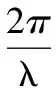
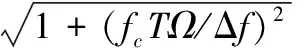
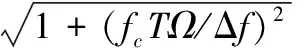
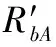
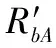
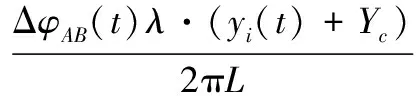
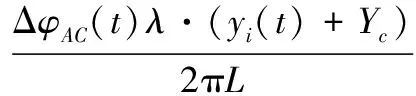
3.3 时变三维成像精度分析
4 仿真验证
4.1 理想条件下时变三维成像

4.2 多散射点时变三维成像


4.3 鲁棒性分析

5 结 论
