弹性基底粘接薄板起皱的非局部分析

彭香武,赵建中,郭兴明

微纳米薄膜/基底结构系统在纳机电系统(nano electro-mechanical system,NEMS)中有着十分重要的地位.在复合微纳电子组件(薄膜、基底、封装)生产过程中,由于热学与力学参量的失配,薄膜在各种成型工艺过程的加热冷却,会引起残余热应力或错位应变,从而使得NEMS失效.事实上,Bowden等[1]和Chen等[2]通过实验发现,弹性基底加热后粘合一层薄膜,待系统冷却后,未脱粘的薄膜会自发形成有序的结构(起皱或屈曲).对于薄膜/基底系统,薄膜发生起皱失稳但仍未脱粘.Allen[3]通过研究夹层板模型,得出临界薄膜力由基底的模量所决定的结论.Cerda等[4]对薄膜起皱的几何和物理原理进行了阐述.Chen等[5]和Song等[6]分别使用数值法和解析法对3种起皱模态所具有的势能进行了分析,其中基底被模拟为半无限空间.Huang等[7]和Li等[8]根据实际基底为有限厚的情况,分别对条纹形和棋盘形的起皱模态进行了非线性分析.Zhou等[9]研究了石墨烯圆片覆盖在球基体上的非局部起皱行为.通过与分子动力方法的模拟结果比较,Yakobson等[10]发现连续介质力学模型在微纳尺度器件的力学问题具有相当的有效性.关于微纳尺度的研究表明需要建立更为精确的理论.Eringen[11-12]通过取消“局部化假设”建立了非局部理论,认为一点处的应力应与整个变形物体的应变有关.Pradhan等[13-14]和Behfar等[15]利用非局部理论研究了纳米板和石墨烯的振动问题.Peng等[16]和刘亮等[17]利用非局部理论对复合粘接材料系统屈曲进行了尺度分析.

本工作研究了粘接在弹性基底上的薄板的单轴受压起皱问题,利用弹性屈曲理论和非局部理论分别对薄板和弹性基底进行了建模,其中界面条件遵循“位移连续”和“零剪切应力”,分析了弹性基底的下表面条件、泊松比以及弹性基底与薄板的厚度比、模量比对薄板系统起皱行为的影响.模型的计算结果对微纳尺度复合材料系统的构建具有参考意义.

1 理论模型与屈曲分析

薄板/弹性基底系统的条纹形起皱如图1所示.由图可以看出,厚度为h的薄板完全粘接在厚度为H的弹性基底上.薄板和弹性基底的弹性模量分别为Ep,Es,泊松比分别为µp,µs.单轴受压的薄板发生条纹形起皱,且起皱过程中薄板和弹性基底粘接完好.

图1 弹性基底上粘接薄板的条纹形起皱Fig.1 Stripes wrinkle of thin plate bonded on an elastic substrate

1.1 薄板的屈曲控制方程

由Kirchhoあ板假设可知,薄板上点(x,y,z)的位移场为

式中,u,v,w为中面上对应点的位移.

薄板的几何方程为

非局部本构方程可表示为[12,16]

薄板的内力和内力矩可表示为

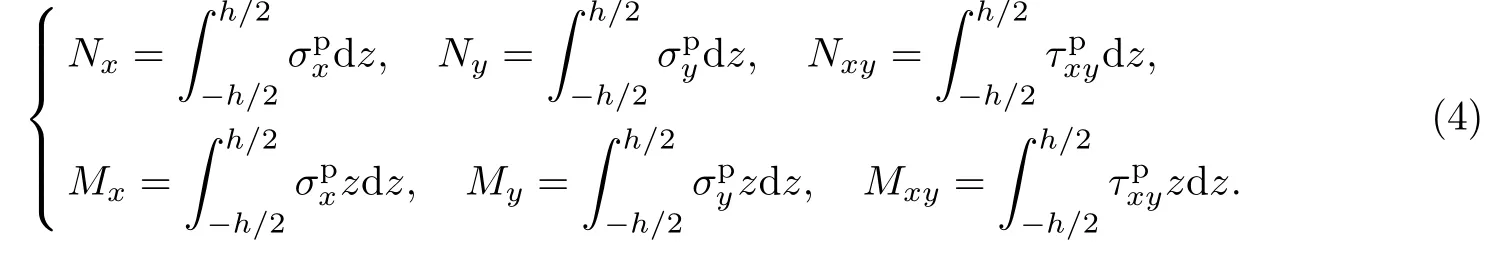
把式(3)代入式(4),则有

若不计体力,则薄板的力和力矩的平衡方程为

式中,q表示弹性基底对薄板的法向作用.

令Nx=N,Ny=0,Nxy=0,则其自然满足式(6)和(7).同时,弹性基底等效为Winkler弹性后,应有q=Kww,其中Kw为对应变形的Winkler弹性系数.薄板的非局部屈曲控制方程可表示为

若考虑薄板的条纹形模态屈曲,则有w=Acos(kx).将其带入式(9),可得

1.2 Winkler弹性系数的计算

当薄板发生条纹形模态起皱时,弹性基底也相应地发生变形,如图2所示.

图2 弹性基底的变形Fig.2 Deformation of elastic substrate

设弹性基底上点(x,z)的位移为(ux,uz),则其应变为

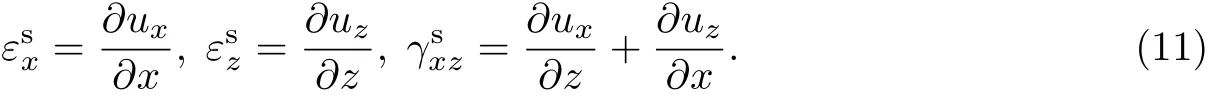
从而,应变协调方程可表示为

弹性基底的非局部本构方程为[12]

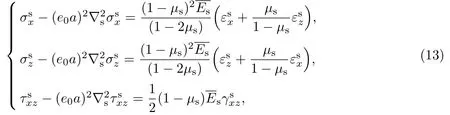
若忽略体力,弹性基底的受力平衡方程为

联立式(12),(13)和(14),可推得应力函数表示的相容方程为

相应的应力分量分别为

假设应力函数Φ(x,z)=F(z)cos(kx),将其代入相容方程(15),整理可得

特征方程为

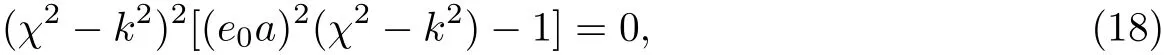
其特征根为

因此,方程(17)的解为

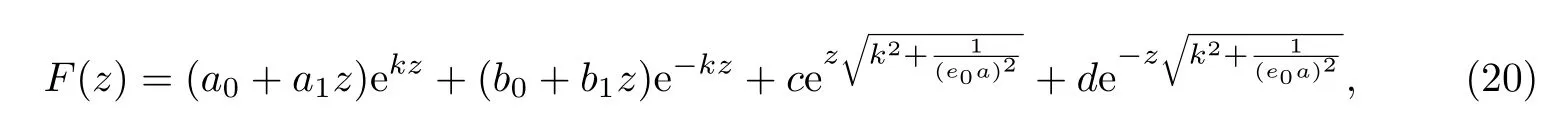
式中,a0,a1,b0,b1,c,d都是待定系数.

从而,所求的应力函数为

进而,相应的应力分量分别为

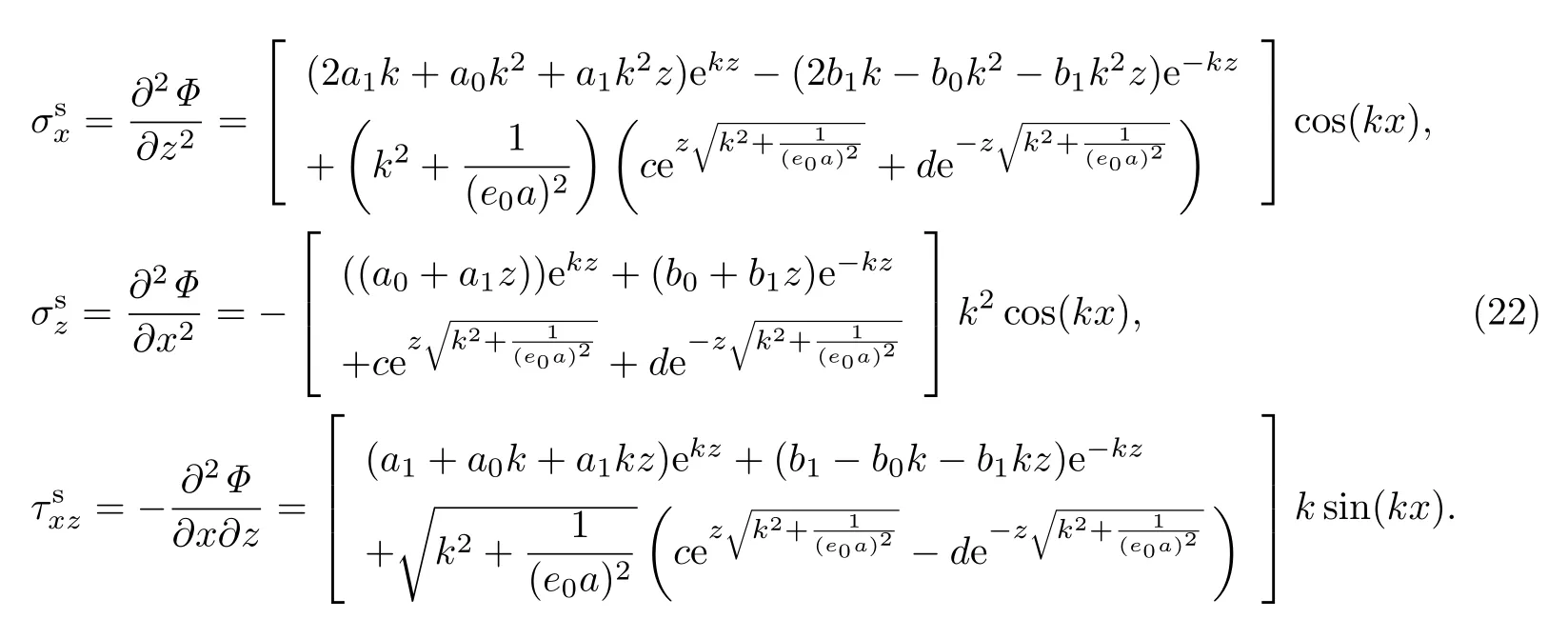
对应的位移分别为

下面考虑弹性基底的边界条件.若弹性基底下表面为完全粘接界面,此时弹性基底上表面与表层板粘结,其变形应与薄板的条纹形模态一致,且剪应力为0,下表面与刚性支撑完全粘接,其位移也为0,即有

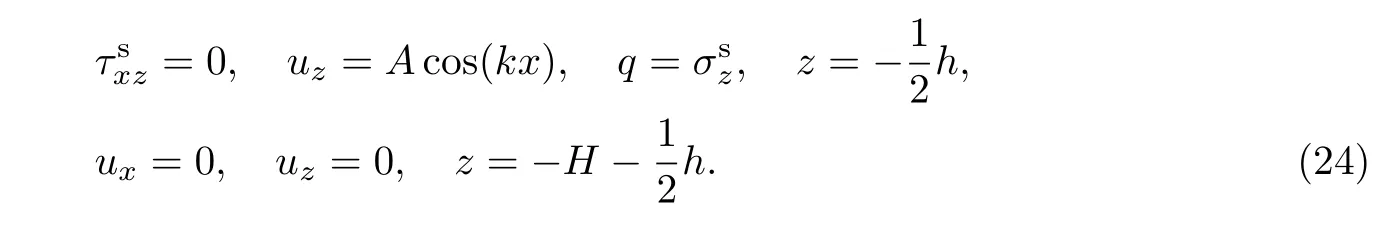
另外,当非局部参数退化为0时,应有

联立式(24)和(25),最终得到Winkler弹性系数为

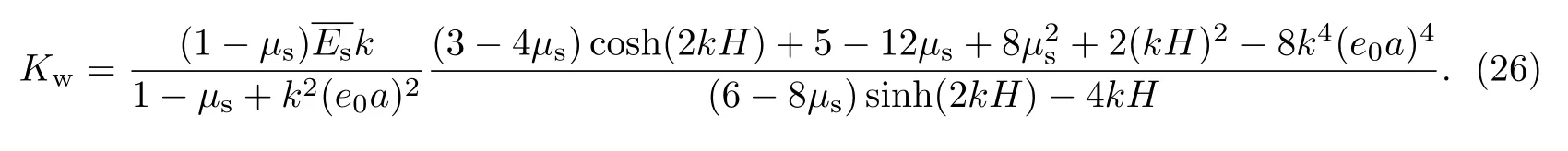
若弹性基底的下表面为滑动界面,则弹性基底的下表面所受剪应力为0.同时,弹性基底的上表面与薄板粘结,其变形应为条纹形,且剪应力为0.因此有

同样,式(25)也成立.

联立式(25)和(27),最终得到Winkler弹性系数为

2 算例与讨论

下面讨论非局部理论下各种参数对系统屈曲行为的影响,首先引进如下无量纲参数:

2.1 弹性基底的下表面

当弹性基地的下表面不同时,计算得到的Winkler弹性系数也不同,因此需要了解下界面条件对薄板起皱行为的影响.取薄板的厚度h=10 nm,弹性基底的泊松比µs=0.4,薄板与弹性基底的模量比=100,弹性基底与薄板的厚度比H/h=10,则可得到不同界面下非局部参数e0a对临界载荷的影响,结果如图3所示.

图3 非局部参数对临界载荷和波长的影响Fig.3 Eあects of nonlocal parameter on critical load and wavelength

由图3可以看出:不论是完全粘接界面还是自由滑动界面,起皱载荷Nc和波长λc均随着非局部参数e0a的增大而下降;与自由滑动界面相比,完全粘接界面下的临界载荷Nc更大,而波长λc更小.

2.2 泊松比µs

弹性基底决定了Winkler弹性系数,因此弹性基底的泊松比影响薄板起皱行为.图4为完全粘接界面下临界载荷比和波长比关于泊松比µs的变化,其中为经典连续介质力学(非局部参数e0a=0)中对应的临界载荷和波长.薄板的厚度h=10 nm,弹性模量比=100和厚度比H/h=10.

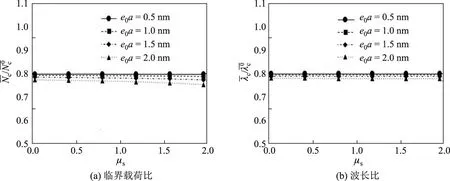
图4 临界载荷比和波长比关于泊松比的变化Fig.4 Curves of critical load ratio and wavelength ratio on Poission ratio

由图4可以看出:非局部参数e0a越大,临界载荷比随着泊松比µs的增大而下降的趋势越明显;波长比随着泊松比µs的变化基本不变.由此可见,引入非局部参数e0a后,薄板发生起皱时的临界载荷对弹性基底的不可压缩性变得敏感,而波长不受影响.

2.3 厚度比H/h

弹性基底和薄板的厚度比对Winkler弹性系数的影响较大,因此对薄板起皱行为也有影响.图5为完全粘接界面下临界载荷比和波长比关于厚度比H/h的变化,其中薄板的厚度h=10 nm,弹性基底的泊松比µs=0.4,弹性模量比=100.固定非局部参数e0a的情况下,临界载荷比和波长比均随着厚度比H/h的增大而增大,且趋于1.由此可见,弹性基底越薄,非局部效应越显著.另外,弹性基底的厚度远大于薄板时,非局部效应可忽略.

图5 临界载荷比和波长比关于厚度比的变化Fig.5 Curves of critical load ratio and wavelength ratio on thickness ratio

2.4 薄板与弹性基底的模量比

临界载荷和波长的表达式中均含有表示薄板和弹性基底的模量比的变量,因此模量比对薄板的起皱行为有影响.图6为完全粘接界面下临界载荷比和波长比关于模量比的变化,其中薄板的厚度h=10 nm,弹性基底的泊松比µs=0.4,厚度比H/h=10.由图6可以看出:随着模量比的增大,临界载荷比和波长比均增大,且趋于1;对于较小的模量比,非局部参数e0a越大,临界载荷比和波长比的数值越小.因此,对于粘接在弹性基底的薄板系统,弹性基底的模量比薄板更大时,薄板的起皱行为具有显著的非局部效应.

3 结束语

本工作基于非局部理论对弹性基底上粘接薄板的起皱问题进行了研究,分析了弹性基底的下表面、泊松比以及薄板与弹性基底的厚度比、模量比对薄板起皱行为的影响.研究结果表明,非局部参数的引入降低了薄板的有效抗弯刚度和弹性基底对薄板的法向作用,从而使得薄板发生起皱所需的载荷和起皱波长均减小.因此,对于厚软的弹性基底,薄板系统的非局部效应可忽略.

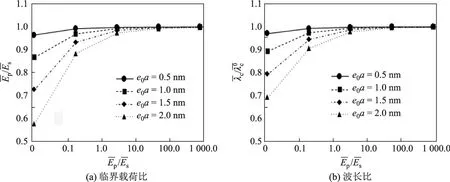
图6 临界载荷比和波长比关于杨模量比的变化Fig.6 Curves of critical load ratio and wavelength ratio on modulus ratio

[1]BOWDEN N,BRITTAIN S,EVANS A G,et al.Spontaneous formation of ordered structures in thin fi lms of metals supported on an elastomeric polymer[J].Nature,1998,393(6681):146-149.

[2]CHEN X,HUTCHINSON J W.A family of herringbone patterns in thin fi lms[J].Scripta Materialia,2004,50(6):797-801.

[3]ALLEN H G.Analysis and design of structural sandwich panels[M].Oxford:Pergamon Press Ltd,1969:38-132.

[4]CERDA E,MAHADEVAN L.Geometry and physics of wrinkling[J].Physical Review Letters,2003,90:074302.

[5]CHEN X,HUTCHINSON J W.Herringbone buckling patterns of compressed thin fi lms on compliant substrates[J].Journal of Applied Mechanics,2004,71(5):597-603.

[6]SONG J,JIANG H,CHOI W M,et al.An analytical study of two-dimensional buckling of thin if lms on compliant substrates[J].Journal of Applied Physics,2008,103(1):014303.

[7]HUANG Z Y,HONG W,SUO Z.Nonlinear analysis of wrinkles in a fi lm bonded to a compliant substrate[J].Journal of Mechanics and Physics of Solids,2005,53:2101-2118.

[8]LI B,HUANG S Q,FENG X Q.Buckling and postbuckling of a compressed thin fi lm bonded on a soft elastic layer:a three-dimensional analysis[J].Archive of Applied Mechanics,2010,80:175-188.

[9]ZHOU Y G,CHEN Y L,LIU B,et al.Mechanics of nanoscale wrinkling of graphene on a nondevelopable surface[J].Carbon,2015,84:263-271.

[10]YAkOBSON B I,BRABEC C J,BERNHOLC J.Nanomechanics of carbon tubes:instabilities beyond linear response[J].Physcial Review Letters,1996,76(14):2511-2514.

[11]ERINGEN A C.On diあerential equations of nonlocal elasticity and solutions of screw dislocation and surface waves[J].Journal of Applied Physics,1983,54(9):4703-4710.

[12]ERINGEN A C.Nonlocal continuum fi eld theories[M].New York:Springer-Verlag,2002:71-175.

[13]PRADHAN S C,PHADIkAR J K.Nonlocal elasticity theory for vibration of nanoplates[J].Journal of Sound and Vibration,2009,325(1/2):206-223.

[14]PRADHAN S C,MURMU T.Small scale eあect on the buckling analysis of single-layered graphene sheet embedded in an elastic medium based on nonlocal plate theory[J].Physica E:Lowdimensional Systems and Nanostructures,2010,42(5):1293-1301.

[15]BEHFAR K,NAGHDABADI R.Nanoscale vibrational analysis of a muti-layered grapheme sheet embedded in an elastic medium[J].Composites Science and Technology,2005,65(7/8):1159-1164.

[16]PENG X W,GUO X M,LIU L,et al.Scale eあects on nonlocal buckling analysis of bilayers composite plates under non-uniform loads[J].Applied Mathematics and Mechanics(English Edition),2015,36(1):1-10.

[17]刘亮,彭香武,王青占,等.粘接材料及结构在双轴受压和温度耦合作用下变形的尺度效应和非局部效应分析[J].上海大学学报(自然科学版),2015,21(4):422-431.

[18]LIM C W.On the truth of nanoscale for nanobeams based on nonlocal elastic stress f i eld theory:equilibrium,governing equation and static def l ection[J].Applied Mathematics and Mechanics(English Edition),2010,31(1):37-54.

[19]吴连元.板壳稳定性理论[M].武汉:华中理工大学出版社,1996:19-68.

[20]黄义,何芳社.弹性地基上的梁、板、壳[M].北京:科学出版社,2005:49-74.

[21]徐芝纶.弹性力学简明教程[M].3版.北京:高等教育出版社,2008:9-21.