典型松散体边坡滚石运动距离的运动学分析

张亚辉, 张孟喜,陈 强,王 东,罗康军

滚石运动是指物源区的石块由于受到某种扰动,由静止开始,通过下滑、碰撞弹跳、滚动等运动方式到达坡底,最后在平缓的地带静止下来的动力学过程[1-3].滚石灾害多发生于山区,具有破坏性强的特点,较大的滚石会堵塞甚至砸坏公路.因此,对于边坡上部物源区滚石较为丰富的公路路段需要进行合理绕避来防止滚石灾害,绕避距离便成了问题的关键.

对于滚石的运动轨迹和距离,国外学者进行了较为丰富的研究,如罗依尼维里教授提出的落石运动轨迹预测公式[4]和根据牛顿碰撞理论建立的计算公式[5],Dorren[6]提出了达角模型(reach angle model)、影锥角模型(shallow angle model)等.国内对滚石运动的研究起步较晚.刘丹等[7]通过落石的模型试验,讨论了落石的质量、形状和下滑高度等对落石水平运动距离的影响.俸锦福等[8]利用分段循环算法得到了滚动、抛物运动和坡面碰撞共3个运动阶段的运动速度计算公式.杨海清等[9]基于接触力学和运动学理论,将落石近似成椭圆形,提出了一种新的滚石运动轨迹预测公式.程强等[10]在实测汶川地震近400条崩塌滚石剖面的基础上,通过统计分析研究了滚石运动特征和危害范围参数.崔圣华等[11]通过现场试验,得到了总体平直、角度局部变化的直线型斜坡滚石速度估算公式,进而估算了滚石的运动速度和冲击能量.黄润秋等[12]通过现场试验分析了坡面特征对滚石停留位置、运动时间以及不同形状的滚石运动特征的影响.

目前,国内外滚石运动轨迹和距离的研究大多局限于影响因素的现场试验分析和经验公式,而对滚石运动距离精确计算以及影响因素分析等问题研究较少.因此,本工作从运动学的角度,结合震后公路松散体边坡滚石运动的过程和特点,通过理论分析建立了合理的数学模型,推导出考虑滚石自转影响的运动距离计算公式,并对影响因素进行了定量的分析,同时结合某边坡工程现场试验,构建了Rocfall动态数值模型,验证了计算公式的准确性和可行性.研究成果对山区道路绕避距离的确定具有指导意义.

1 滚石运动距离

1.1 计算图式

图1为汶川地震后都汶公路沿线的典型坡面,该坡面可分为3段:陡坡段、缓坡段和平直段.陡坡段基本上都是基岩裸露,坡角一般较大;缓坡段,由上部崩塌而堆积的松散堆积体构成,坡度一般较为平缓,恢复系数比较小.现场调查显示,这种坡型所占的比例较大.因此,本工作主要讨论滚石在该坡型上的运动.实际情况下,滚石可以从坡面上任一点脱落,但考虑到最不安全的情形,认为滚石在最高点由于受到某种扰动,从静止开始沿①段滚下,到达②段发生碰撞弹跳,产生自转角速度,之后沿坡面滚动,到达坡底,再次发生碰撞弹跳,当竖向速度小于某一值时开始滚动,直至静止.

图1 汶川地震后都汶公路沿线的典型坡面Fig.1 Typical slope along Duwen Road after Wen Chuan earthquake

另外,陡坡段中可能存在缓坡段,但是坡角一般较小,滚石滚下到达该缓坡段底端的速度较小,可以忽略不计.

对于其他不能简化为图1所示坡型的边坡,本工作不作考虑.

1.2 影响因素

滚石的最终运动距离,取决于滚石到达坡底的速度以及平直段的恢复系数.因此要确定滚石运动距离,只需考虑滚石到达坡底速度的影响因素.由运动学原理可知,滚石在坡面上运动一般是加速运动的,则到达坡底的速度与滚石在坡面上运动的时间、加速度有关系.坡高越大,滚石在坡面上运动的时间越长;坡角越大,滚石运动的加速度越大;坡面越光滑,滚石所受到的摩擦力越小,加速度越大.综上可得,滚石运动距离与坡高、坡角、坡面恢复系数以及坡面状态有关.

滚石运动的计算图式如图2所示,其中粗实线为滚石运动的轨迹.图2中:h1,h2分别为陡坡段和缓坡的坡高;θ1,θ2分别为陡坡段和缓坡段的坡角;ϕ1,ϕ2,ϕ3分别为等效坡面休止角.等效坡面休止角是滚石能够从坡顶静止下滑的最小角度,取值与滚石形状、运动状态和坡面的粗糙程度等有关.对于同一边坡,近似于球形的滚石的ϕ值比其他形状要小;对于相同的滚石,在光滑坡面上的ϕ值大于粗糙坡面;滚动时的ϕ值比滑动时小得多.RNi,RTi(i=2,3)为坡面各坡段的法向、切向恢复系数,值为该方向上碰撞后速度与碰撞前速度的比值.由于恢复系数在碰撞弹跳过程中才有意义,因此①段的恢复系数对于滚石运动距离几乎没有影响.坡面恢复系数的取值参考表1.S为滚石的最终运动距离,即滚石最终静止位置到C点的距离.

图2 滚石运动轨迹的计算图式Fig.2 Calculation chart of rockfall trajectory

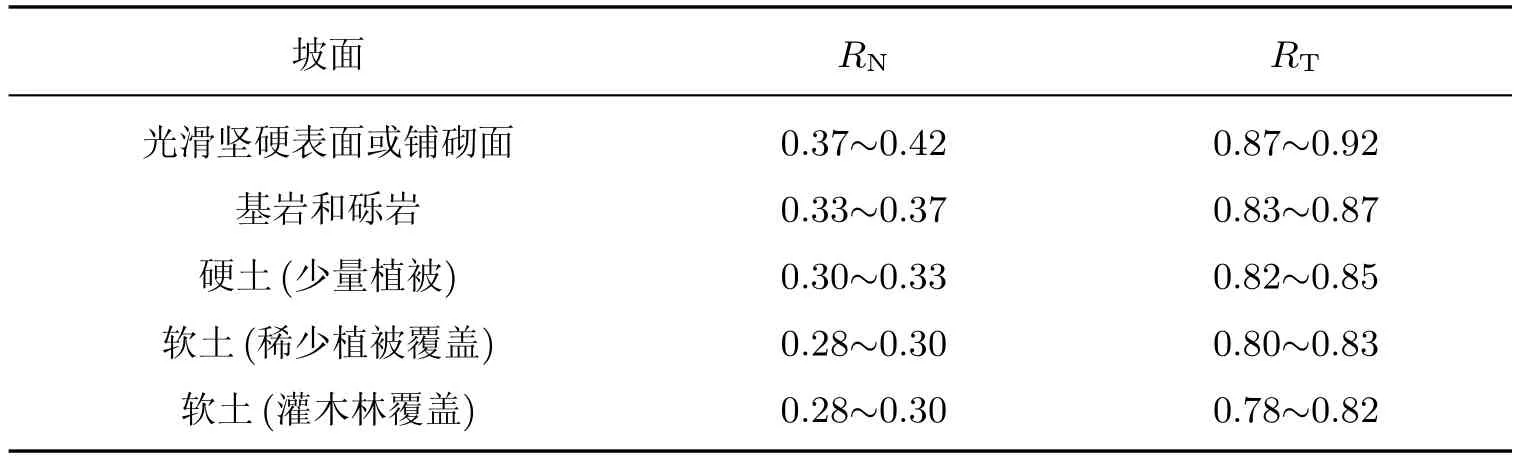
表1 不同坡面的法向、切向恢复系数Table 1 Coeきcients of restitution in normal and tangential directions of diあerent slopes

1.3 基本假定

从现场的观测和试验分析的结果可知,滚石在坡面上的运动是先在陡坡段滚动,然后在变坡点碰撞弹跳,接着在缓坡段滚动,之后又弹跳碰撞,最后滑动.但为了便于理论分析,做如下假设.

(1)计算过程中忽略滚石之间的相互影响,且运动过程中忽略空气阻力.

(2)考虑滚石平动时,将滚石简化为一个质点;考虑滚石转动时,将滚石简化为一刚性的均质球体.

(3)滚石的碰撞属于刚体碰撞,碰撞过程中动能的损失通过恢复系数来考虑,且各坡段的恢复系数为恒定值.

1.4 计算过程

为了便于分析滚石运动的整个过程,按照坡段把全过程分为陡坡段、缓坡段和平直段进行分析.

1.4.1 陡坡段

根据现场观测,陡坡段的坡角大多数小于60°,最大的也不超过65°.由文献[13]可知,边坡坡角小于60°时,滚石表现为滚动.滚石由A点静止开始沿坡面滚下,摩擦系数µ可以看作为tan ϕ.由于ϕ在取值时已考虑滚动的影响,故不再考虑自转.于是,由V2B=2aS,可得

1.4.2 缓坡段

滚石自转对于最终运动距离的影响不能忽略,因此在缓坡段需要考虑滚石的自转.首先引入摩擦函数F1和尺度函数F2,F1和F2的表达式分别为

式中,w为滚石的自转角速度,CF1=6.096 m/s,CF2=76.200 m/s为经验常数.

再令VB2T2=F1×F2×VB2T1.若不考虑自转影响,则无需引入F1和F2,而只考虑碰撞能量损失.

滚石以速度VB在B点发生碰撞,然后开始自转,并产生角速度.缓坡段滚石运动的计算图式和轨迹如图3所示.

滚石与缓坡面第一次碰撞前,有

第一次碰撞后,则由能量守恒定律可得

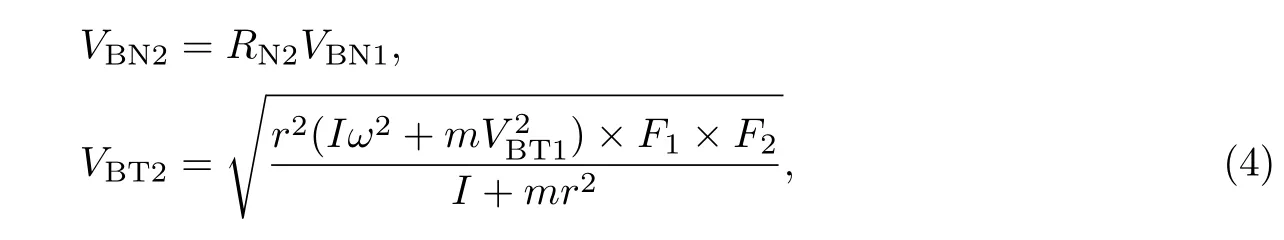
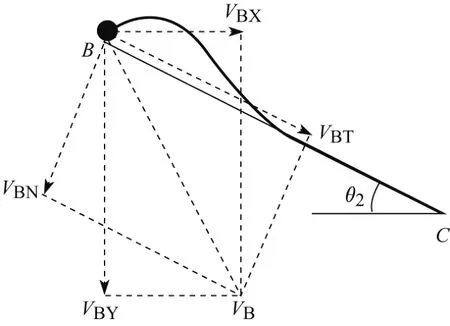
图3 缓坡段滚石运动轨迹的计算图式Fig.3 Calculation chart of rockfall trajectory on transition slope

将VBN2和VBT2分解至沿坡向和垂直于坡向,可得

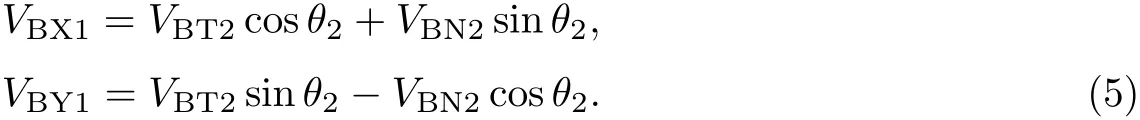
滚石在缓坡面碰撞后做抛物运动,由于一般情况下滚石不会直接到达坡面的平直段,故

滚石在缓坡面第二次碰撞前,有

将VBX2和VBY2分解至沿坡向和垂直于坡向,可得

第二次碰撞后,则有

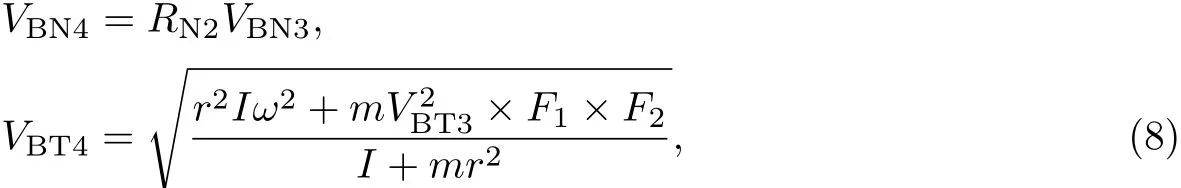
式中,F1,F2对应于第二次碰撞时的状态,即将VBN3,VBT3以及第二次碰撞前的角速度ω代入式(1)求得的结果.

由文献[14]可知,当落石与坡面碰撞后的法向速度为0而切向速度不为0时,落石会沿坡面滚动.由于缓坡段一般是松散堆积体,法向恢复系数RN较小,碰撞后切向速度比法向速度大得多,滚石的运动变为沿切向的滚动,于是有

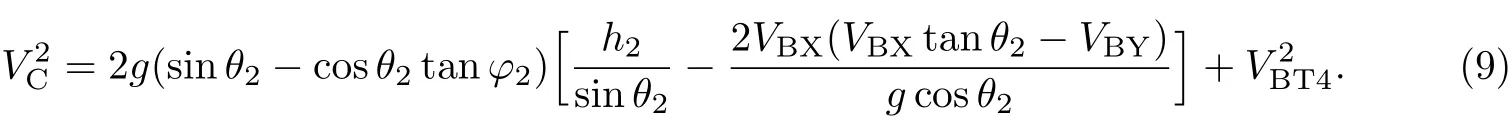
1.4.3 平直段

滚石以速度VC在C点发生碰撞,之后连续碰撞弹跳,当竖向速度减小到一定程度时,可认为滚石沿坡面运动.由表1可知,平直段坡面的法向恢复系数RN约为0.3,当碰撞两次之后,法向速度约为最初的10%,是一个比较小的值.按照3次碰撞、2次弹跳的情况来考虑,滚石运动的计算图式和运动轨迹如图4所示.

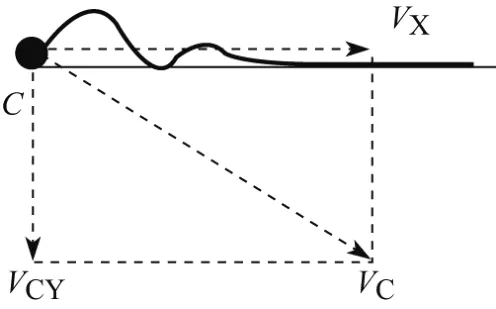
图4 平直段滚石运动轨迹计算图式Fig.4 Calculation chart of rockfall trajectory on straight section

滚石在平直段坡面第一次碰撞前,有

将VCT1,VCN1,ωC,RN3,RT3代入式(2)可以得出F1,F2.

第一次碰撞后,则有

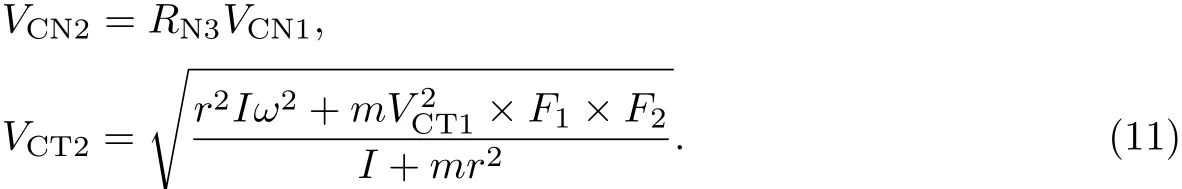
滚石在平直段坡面的第一段弹跳距离为

之后由于滚石的速度和角速度较小,自转对于弹跳距离的影响较小,可以忽略不计,因此只考虑碰撞的动能损失.

滚石在平直段坡面第二次碰撞后,有

第二段弹跳距离为

滚石在平直段坡面第三次碰撞后,有

之后滚石沿平直段坡面运动直至停止,运动距离为

综上可得,滚石的最终运动距离为

若以S′表示滚石停止点到下落点的距离,则

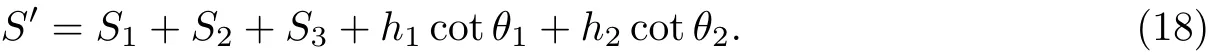
1.5 对比验证

选取文献[3]中球形滚石的4组现场试验(S9,S10,S11,S12),试验场地剖面如图5所示.坡面长度约为62.8 m;AB段坡角约为40°,垂直高度约为20.0 m;BD段坡角约为35°,垂直高度约为18.1 m;AC段坡面主要为石灰渣,胶结良好;CD段坡面主要为花岗岩石材碎渣,较松散.选取质量为11 kg的近似于球形的石块,到达坡面D点的速度为18.93 m/s,平台段的摩擦系数为0.48,最终滚动距离为11 m.据此,利用Rocfall软件建立边坡模型,模型的参数取值如表2所示.

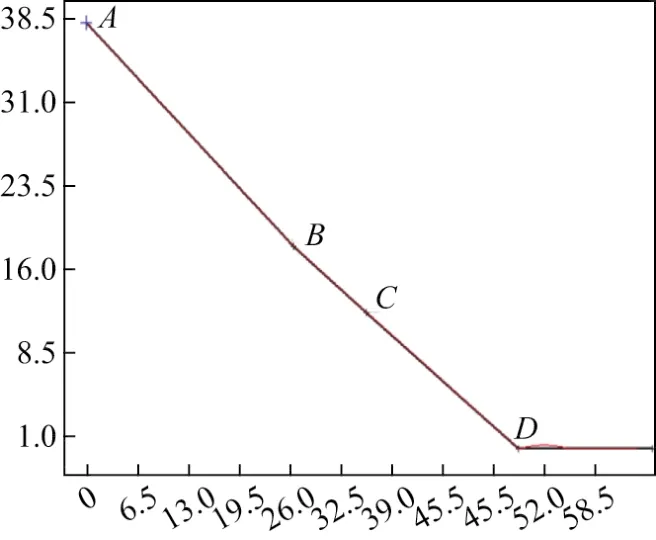
图5 Rocfall建立模型及轨迹Fig.5 Rocfall model and motion trail

表2 边坡模型参数的取值Table 2 Value of every parameter in program Rocfall

需要说明的是:RN2,RT2是根据表1选取的值,ϕ1,ϕ2取值是在合理的取值范围内使滚石到达坡底的速度最接近于所测得的速率所确定的,其余的数据均为文献[3]中所给出的数值,ϕ3是滚动摩擦系数所还原的角度值.另外,由于本工作研究的是单个滚石在固定的位置静止下滑的情况,因此在Rocfall软件中RN和RT的取值将标准差定为0,且得到的轨迹可以看做是单一的.

Rocfall是一款用于分析滚石运动轨迹及防治措施的软件,能够计算出滚石在运动过程中,各个位置的速度、动能、弹跳高度等的取值和分布,同时也能得到滚石最终静止的位置.

通过公式计算、Rocfall软件和现场实测三种方式分别得到的滚石运动距离如表3所示.

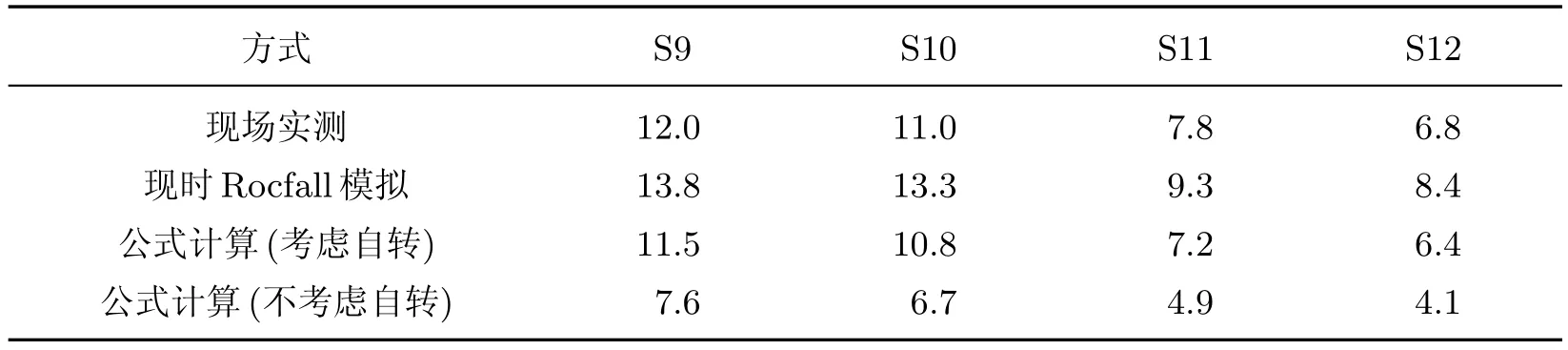
表3 三种方式求得滚石运动距离的比较结果对比Table 3 Comparison on the result of three methods for calculating distance of rockfall m

由表3可以看出,Rocfall软件模拟的结果比现场试验数据大,这是由于模拟并未考虑实际情况下中坡面凹凸不平的情况.公式的计算结果比现场试验结果要小,这是由于计算图式只考虑滚石在缓坡段和平直段的2次弹跳,与实际情况不符,其中不考虑自转的情况下,数据与实际相差较大,说明自转对于滚石运动距离的影响较大.综上可知,公式计算和Rocfall模拟的结果与现场试验结果相差不大,可用于指导工程实践,并且在公式计算中应该考虑滚石自转的影响.

2 滚石运动距离的影响因素

滚石运动距离的影响因素包括坡高、坡角、坡面还原系数、坡面形式和滚石运动形式、大小等.下面选取5个典型的影响因素进行分析.

2.1 陡坡段坡角

陡坡段坡角对滚石运动距离的影响主要是通过改变滚石到达缓坡段的速度来实现的.坡角θ1不同时滚石的运动距离S如表4所示,二者的关系曲线如图6所示.

表4 陡坡段坡角不同时滚石的运动距离Table 4 Distance of rockfall at diあerent slope angle of steep slope

图6 陡坡段坡角与滚石运动距离的关系Fig.6 Curvilinear relationship between slope angle of steep slope and distance of rockfall

由图6可以看出:曲线以45°左右为转折点,当陡坡段坡度小于45°时,滚动距离随陡坡段坡角增大而增大;当陡坡段坡角大于45°时,滚动距离随陡坡段坡度增大而减小.这主要是因为滚石的运动距离与水平速度和运动时间有关,而运动时间是由竖向速度决定的.随着坡角的增大,滚石的水平速度减小,竖向速度增加,运行时间增加.水平速度和运动时间两个因素综合影响,在陡坡段坡角为45°时滚石的运动距离取最大值.

2.2 法向恢复系数

法向恢复系数对于滚石运动距离的影响主要是通过改变滚石与坡面碰撞后的竖向速度,从而改变滚石空中的弹跳时间来实现的.由于陡坡段和缓坡段坡角相差不大,在交接点处发生碰撞的效果不明显,因此取平直段的恢复系数进行研究.由表1可知,坡面的法向恢复系数主要在0.25∼0.45取值.法向恢复系数RN3不同时滚石的运动距离S如表5所示,二者的曲线关系如图7所示.

表5 法向恢复系数不同时滚石的运动距离Table 5 Distance of rockfall at diあerent normal coeきcient of restitution

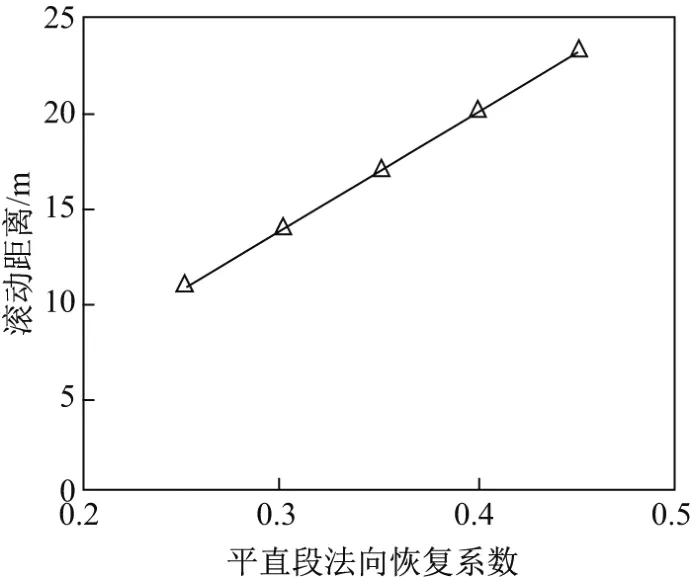
图7 法向恢复系数与滚石运动距离的关系Fig.7 Curvilinear relationship between normal coeきcient of restitution and distance of rockfall

由图7可以看出,运动距离随平直段法向恢复系数的增大而增大.这主要是因为随着法向恢复系数的增大,碰撞后滚石的竖向速度增大,滚石在空中运行的时间越长,因此在水平速度不变的情况下,滚石的运动距离也就越大.

2.3 切向恢复系数

切向恢复系数对于滚石运动距离的影响主要是通过改变碰撞后滚石的水平速度来实现的.由表1可知,法向恢复系数主要在0.75∼0.95取值.法向恢复系数RT3不同时滚石的运动距离S如表6所示,二者的关系曲线如图8所示.

表6 切向恢复系数不同时滚石的运动距离Table 6 Distance of rockfall at diあerent tangential coeきcient of restitution

图8 切向恢复系数与滚石运动距离的关系Fig.8 Curvilinear relationship between tangential coeきcient of restitution and distance of rockfall

由图8可以看出,运动距离随平直段切向恢复系数的增大而增大.这主要是因为随着切向恢复系数的增大,碰撞后滚石的水平速度增大,而竖向速度没有变化,即碰撞后滚石在空中运行时间不变,因此滚石的运动距离变大.

2.4 坡面休止角

坡面休止角对于运动距离的影响主要是通过改变滚石在坡面运动的加速度,进而改变到达坡角的速度来实现的.由于滚石到达缓坡段发生弹跳碰撞,在坡面运动的距离可能较短,而滚石在陡坡段是一直沿着坡面下滑的,因此选取陡坡段的坡面休止角作为研究对象.实际情况下滚石在坡面上滑动时,坡面休止角一般为15°∼40°.坡面休止角ϕ1不同时滚石的运动距离S如表7所示,二者的曲线关系如图9所示.

表7 坡面休止角不同时滚石的运动距离Table 7 Distance of rockfall at diあerent slope of repose

图9 坡面休止角与滚石运动距离的关系Fig.9 Curvilinear relationship between slope of repose and distance of rockfall

由图9可以看出,滚石的运动距离随着坡面休止角的增大而减小.因为随着坡面休止角的增大,滚石在坡面运动过程中受到的摩擦力越大,则滚石到达坡底的速度越小,因此滚石的最终运动距离越小.

2.5 坡高

坡高对于运动距离的影响也是通过改变滚石到达坡底的速度来实现的,但是与坡面休止角不同,坡高主要是改变滚石在坡面的运动距离和时间,进而影响滚石到达坡底的速度.同理,取陡坡段坡高作为研究对象,则坡高不同时滚石的运动距离S如表8所示,二者的曲线关系如图10所示.

表8 不同坡高及其对应的滚石运动距离Table 8 Distance of rockfall at diあerent height of slope

图10 坡高与滚石运动距离的曲线关系Fig.10 Curvilinear relationship between height of slope and distance of rockfall

由图10可以看出,滚石运动距离随着坡高的增大而增大.这主要是因为随着坡高的增大,在坡角不变的情况下坡面长度增加,即滚石在坡面加速运行的时间变长,因此到达坡底的速度增加,从而使得滚石的运动距离增大.

3 结论

本工作推导了考虑滚石自转的典型松散体边坡滚石运动距离的计算公式,并对其影响因素进行分析,主要得到以下结论.

(1)针对文献[3]中的算例,若不考虑滚石自转的影响,计算结果与试验测量结果相差较大,这表明滚石自转对于运动距离的影响较大.

(2)陡坡段坡角对于滚石运动距离的影响关系曲线近似于抛物线.在坡角小于45°时,滚石的运动距离随着坡角的增大而增大;当坡角大于45°时,滚石的运动距离随着坡角的增大而减小.

(3)切向恢复系数、法向恢复系数和陡坡段坡高均与滚石的运动距离正相关,即滚石的运动距离随着3种因素的增大而增大.

(4)陡坡段坡面休止角与运动距离负相关,即滚石运动距离随着坡面休止角的增大而减小.

[1]赵耀,王浩,龚匡周,等.边坡滚石运动轨迹分析及坡形坡率设计[J].土工基础,2014,28(4):82-85.

[2]黄雨,孙启登,许强.滚石运动特性研究新进展[J].振动与冲击,2010,29(9):31-35.

[3]黄润秋,刘卫华.滚石在平台上的运动特征分析[J].地球科学进展,2008,23(4):517-523.

[4]BOBBERT M,HUIjING P,Schenau G.Instantaneous torque-angular velocity relationships during jumping[J].Journal of Biomechanics,1985,18(6):553-553.

[5]CHAU K T,WONG R H C,WU J J.Coeきcient of restitution and rotational motions of rockfall impacts[J].International Journal of Rock Mechanics and Mining Sciences,2002,39(1):69-77.

[6]Dorren L.A review of rockfall mechanics and modelling approaches[J].Progress in Physical Geography,2003,27(1):69-87.

[7]刘丹,叶四桥,杨威.落石水平运动距离影响因素的模型试验研究[J].水文地质工程地质,2013,40(5):112-116.

[8]俸锦福,张俊红,朱彬,等.边坡滚石运动轨迹分段循环算法[J].中国地质灾害与防治学报,2011,22(3):96-101.

[9]杨海清,周小平.边坡落石运动轨迹计算新方法[J].岩土力学,2009,30(10):3411-3416.

[10]程强,苏生瑞.汶川地震崩塌滚石坡面运动特征[J].岩土力学,2014,35(2):772-776.

[11]崔圣华,裴向军,黄润秋.直线型斜坡滚石运动速度特征研究[J].工程地质学报,2013,21(5):912-919.

[12]黄润秋,刘卫华,周江平,等.滚石运动特征试验研究[J].岩土工程学报,2007,29(8):1296-1302.

[13]胡厚田.崩塌与落石[M].北京:中国铁道出版社,1989.

[14]吕庆,孙红月,翟三扣,等.边坡滚石运动的计算模型[J].自然灾害学报.2003,12(1):79-84.