超快激光脉冲作用下金薄膜温度和介电函数变化的研究

任世为，吴文智

(黑龙江大学 电子工程学院, 哈尔滨 150080)

近年来，基于贵金属纳米薄膜的光学性质，在提高太阳能电池效率[1]、荧光增强[2]、表面增强Raman散射(SERS)[3]、表面等离子体共振(SPR)[4]等领域有广泛研究及应用。当光波在导电介质中传播时，光波的能量不断损耗，或者说光波能量会被介质吸收，这是由于光与固体中的电子、激子、晶格振动以及杂质和缺陷的相互作用而产生的光的吸收。贵金属纳米薄膜将吸收的光能转化为热量，导致金属薄膜周围介质环境的温度升高，形成热传递。通常选用贵金属金(Au)作为研究对象，由于金薄膜紫外和可见光区反射率较低，但在红外区有很高的反射率，并且在空气中不易氧化，贵金属纳米薄膜通常还会作为生物蛋白质样品的载体用于测试，因此，研究贵金属纳米薄膜在温度变化环境中的光学性质，在光热治疗和热传导领域具有重要的意义。

物质的介电函数取决于物质在外场作用下的极化，极化一般可分为电子位移极化、离子位移极化和固有偶极矩的取向极化。由于金属大都属于原子晶体，且内部存在大量的自由电子，因而可将金属晶体想像为淹没在电子海洋中的正离子实列阵，通常不存在固有偶极矩，即使有的金属原子存在固有的偶极矩，但由于晶体结构比较紧密，固有偶极矩也不容易取向。同时考虑到原子核(离子实)的质量比电子大得多，离子运动速度甚微，故离子位移极化的贡献很小，亦可忽略不计。因此，金属的极化主要来自于电子的位移极化[5]。

介电函数是综合物质内部电极化行为的一个主要的宏观物理量。早在1973年Rosei R等[6]讨论了热调制实验中由于温度变化Au能级跃迁造成介电函数的变化。2013年Marini A等[7]使用自由电子模型考虑5个能级跃迁计算了电子温度变化对介电函数虚部和实部的影响。由于入射光可在金属薄膜表面产生很强的近表面等离子体共振效应[8]，近场SPR具备102～106倍的局域增强效果[9]。另外，金膜在表面增强拉曼散射中起到了重要作用，可以通过巯基附着分子，好的生物适应性以及化学稳定等特性，成为生物应用方面的优先选择。因为其独特的非线性光学和电学性质，金薄膜的在生物和纳米技术方面日益引起科学工作者的重视[12]。

基于金膜的基本跃迁性质，从基本的介电函数随入射光波长变化关系出发，讨论金膜的介电函数随温度和反射率的变化关系。通过理论模拟可以得到入射光脉冲加热薄膜的理论曲线，这为光脉冲加热金属表面的微观热传导机理研究提供了一个途径。

1 理论模型

1.1 介电函数随频率的变化

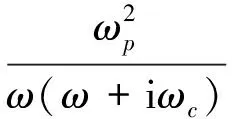
(1)

式中ω表示入射光的频率；ωc表示阻尼频率；ωp表示金属表面等离子共振频率。

该模型在低频情况下与实验数据吻合，在高频情况下有较大误差，在可见光以及更长波长范围，一般使用本模型进行简化计算。在高频波段金属内部的自由电子发生禁带跃迁，需要将式(1)中的1换成ε∞，进行某一特定波长的修正。传统Drude模型的3个假设过于简单，没有考虑自由电子与离子的相互作用，使得理论值与实验数据在近红外以及可见光波段存在较大的误差，根据电子的能带结构提出了基于阻尼振荡的Lorentz-Drude模型。

1.2 自由电子模型

Scouler W J[13]和Rosei R[6]第一次发现了金和铜从d能带到费米能级的带间跃迁形成的光谱调制，这一有趣的性质解释为Fermi smearing。由热导致的金银等金属费米能级以下的非占据态的增加和费米能级以上的非占据态的减少，这一现象称为费米拖尾。在不同波长激光辐照下，由于热调制或者温度变化引起的金介电函数实部和虚部的变化与温度之间的关系。为了更准确地描述金属的介电函数，需要考虑多个能级跃迁，从能级的角度解释，引起虚部ε2变化的原因随着温度的升高扩大了费米能级周围的电子分布和体积应变的展宽，改变了金膜的有效光学性质。虚部的变化可由5项洛伦兹函数来计算：

(2)

由Kramers-Krönig关系得出对应实部的变化，这里P是Cauchy积分主值。

(3)

由于热导致的介电函数实部和虚部变化是非线性的，光照射到金表面加热电子造成的介电函数的变化可以写为:

Δε(ω)=∂Te(Δε1+iΔε2)ΔTe

(4)

1.3 双温模型

超快激光脉冲与金属相互作用时，金属中由于存在的大量自由电子，可通过逆韧致吸收(焦耳加热)过程而吸收激光能量[14]。穿透深度内的自由电子吸收激光能量后，电子温度迅速升高,然后通过自由电子热扩散将热流传入到金属靶材内部,以及通过电子与晶格耦合过程传递给周围晶格。超快激光脉冲与金属相互作用过程可用一维双温模型来描述：

(5)

(6)

2 结果分析

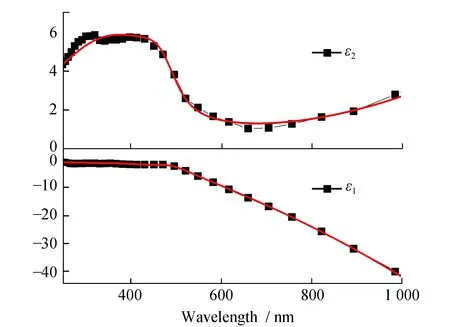
图1 金介电函数的实部和虚部随波长的变化Fig.1 Real (ε1) and imaginary (ε2) of the dielectric function of gold with the change of wavelength

常温下金膜的介电函数随波长的变化关系见图1。图1中实线是在Drude模型的基础上考虑两个带间跃迁的情况下[15-16]，即为Lorentz-Drude模型，所选择的拟合数据可以允许进行非对称线型的调整，使给出的拟合结果更接近于实验值。Lorentz-Drude模型的具体实验拟合参数参考文献[7]，能看到金膜在可见光谱区实部ε1和虚部ε2有较好的拟合结果。对于金，考虑到带间跃迁的影响，带间跃迁阈值能量约为2.2 eV，导致介电常数虚部在560 nm左右快速增大，虚部在500 nm左右变化大，对应一个强吸收过程。

从费米拖尾的能级跃迁定则出发，d能带到Fermi面的跃迁可用来解释Δε2的线型变化，进而通过Kramers-Krönig关系得到Δε1线型变化，由于d能带的跃迁引起的介电常数变化集中在500 nm附近，随着温度的升高，可见费米拖尾的区域不断扩大，向紫外和红外光谱区扩展。模拟中使用的具体参数参见文献[6]。Δε2和Δε1随温度变化的光谱线型见图2。由图2可见，在400～650 nm，介电函数的实部和虚部的变化不是线性的，正负值取决于温度和具体的波长位置。

图2 使用自由电子模型拟合温度变化引起的金介电函数实部和虚部的变化Fig.2 Change of real (ε1) and imaginary (ε2) of the dielectric function of gold under different temperatures using free-electron model

在实际应用中，测量薄膜表面和内部温度有一定难度，多采用光学测量的方法间接得到薄膜的温度分布，其中通过测量薄膜的反射率变化得到薄膜的温度分布就是一种常见的方法。反射率的变化与介电函数的变化关系，由基本的菲涅尔反射式可得[17]：

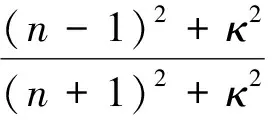
(7)

(8)

(9)

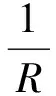
(10)

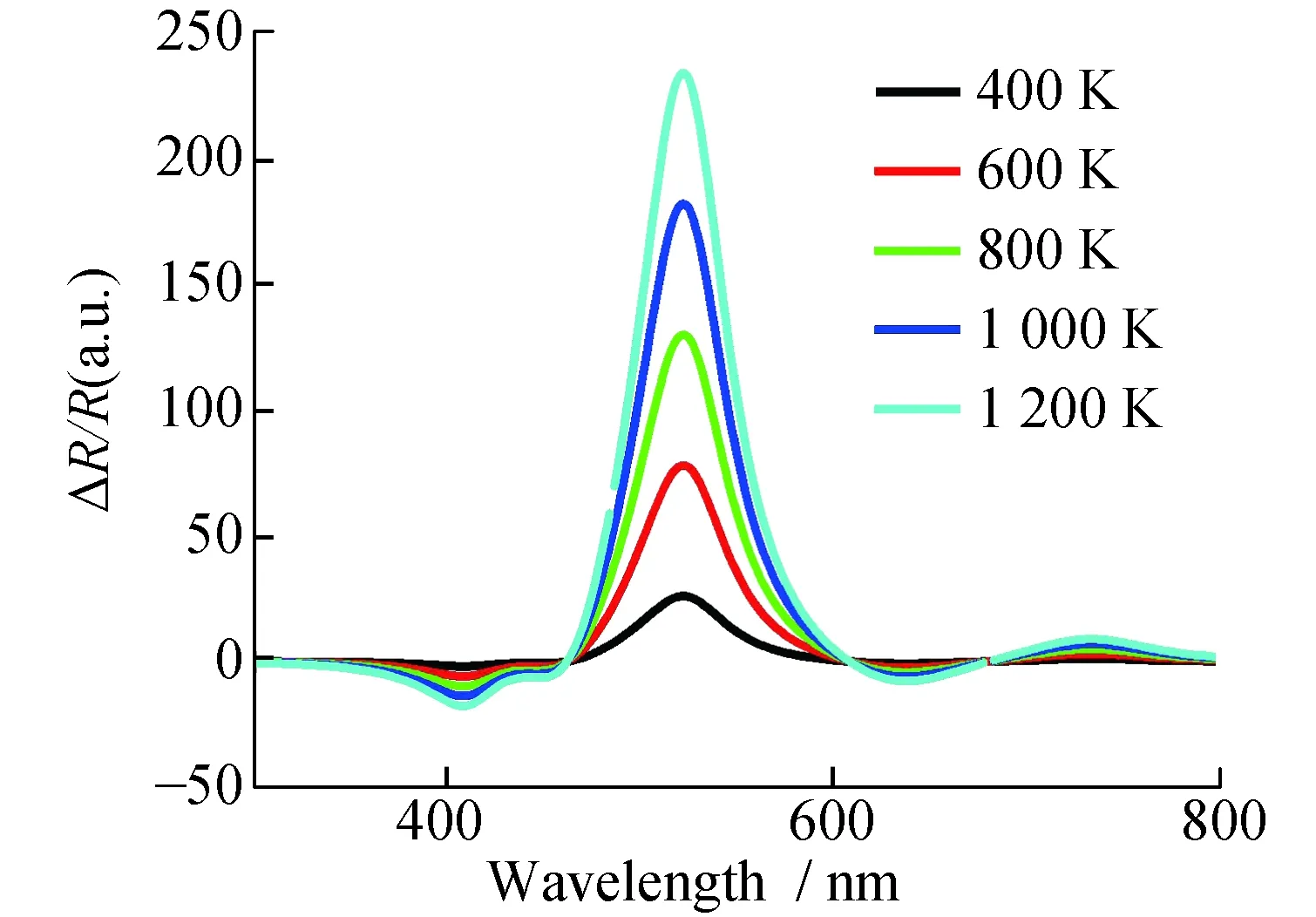
图3 不同温度下的金膜的反射率随波长的变化Fig.3 Wavelength dependence of the change of reflectivity of gold film at different temperatures

考虑介电函数的实部和虚部是波长的函数，利用图1中的实验结果可以直接计算得到式(9)和式(10)的结果，结合通过模拟得到的不同温度下介电函数实部和虚部的变化，能够得到不同波长处某一温度下反射率的变化曲线见图3。可以得到某一特定波长下的温度引起的瞬态反射率相对变化。结合热传导方程可以用于模拟计算某特定波长激光脉冲作用下金薄膜的反射率变化。再从双温模型出发，利用有限元差分法对激光脉冲与金属表面作用后的温度变化进行求解，得到不同作用时间的温度情况。不同激发光功率下的电子和晶格温度随时间的变化关系见图4(a)。分别以超快激光脉冲与金膜相互作用为例。在超快激光脉冲作用下，金薄膜处于非平衡态，由于电子比热容小和响应时间快，电子温度迅速升高，而晶格温度逐渐变高主要是由于自由电子与晶格发生碰撞导致升温。随着激发激光功率的增加，能够看到电子和晶格温度都持续升高，在这一过程中考虑到电子温度对介电函数占主要贡献，通过计算可以得到不同波长激光激发下的表面反射率的变化曲线，400 nm和520 nm激光激发下的表面反射率的变化见图4(b)。由于这里对介电函数影响大的是电子温度，在这一非平衡状态下笔者不考虑晶格温度对介电函数和反射率的贡献。由图4(b)可见，波长变化对热传导过程影响不大，但不同位置对应的反射率变化不同，即520 nm超快激光脉冲激发下金膜的反射率变化增加，而400 nm超快激光脉冲激发下金膜的反射率变化为负值。这与使用泵浦探测技术测量金膜得到的实验结果[16]相吻合，但具体的波长位置有所不同。

图4 (a)不同激发功率下金薄膜的电子和晶格的温度变化;(b)计算得到的不同波长激光激发下的反射率变化Fig.4 (a) With interaction time increasing, the change of surface electron and lattice temperature for gold film at different laser powers;(b) Normalized ΔR/R of gold film at different excited wavelength

3 结 论

从金薄膜的介电函数随波长变化模型出发，结合Lorentz-Drude模型，得到可见光和近红外区域不同温度下金纳米薄膜的介电函数的实部和虚部变化，推导得到不同温度下金纳米薄膜反射率的瞬时变化。通过超快脉冲与金膜作用过程中用到的双温模型，得到温度随着时间的变化，可以直接带入得到激光脉冲作用下的反射率随时间的变化关系，与实验测量结果比较可加深对激光脉冲加热金属薄膜方面研究工作的理解。

[1] Mei A， Li X，Liu L，et al. A hole-conductor-free, fully printable mesoscopic perovskite solar cell with high stability [J]. Science, 2014，345：295-298.

[2] Guidelli E J，Ramos A P，Baffa O. Enhancing and quenching luminescence with gold nanoparticle films: the influence of substrate on the luminescent properties [J]. Nanotechnology,2016，27：15503-15511.

[3] Hu X， Cheng W， Wang T， et al. Fabrication, characterization, and application in SERS of self-assembled polyelectrolyte-gold nanorod multilayered films [J]. The Journal of Physical Chemistry B 2005，109(41)：19385-19389.

[4] 高来勖，叶红安，刘书钢，等.基于显微物镜的表面等离子体共振 [J]. 光子学报，2013，42(9)：1113-1117.

[5] 邝向军. 关于金属介电常数的讨论 [J]. 四川理工学院学报：自然科学版，2006，19(2)：75-78.

[6] Rosei R， Antonangeli F，Grassano U M. D bands position and width in gold from very low temperature thermomodulation measurements [J]. Surface Science, 1973，37： 689-699.

[7] Marini A，Conforti M，Della Valle G，et al. Ultrafast nonlinear dynamics of surface plasmon polaritons in gold nanowires due to the intrinsic nonlinearity of metals [J]. New Journal of Physics,2013，15：013033-013051.

[8] Aigouy L，Boccara A C，Rivoal J C，et al. Experimental observation of localized optical excitations in random metal-dielectric films [J]. Phys. Rev. Lett, 1999，82(22)：4520-4523.

[9] Podolskiy V A，Grésillon S，Buil S，et al. Near-field optical studies of semicontinuous metal films [J]. Phys. Rev. B,2001，64(16)：165403-165417.

[10] Ma W G，Wang H D， Zhang X， et al. Theoretical and experimental study of femtosecond pulse laser heating on thin metal film [J]. Acta Physica Sinica,2011， 60(6)：868-870.

[11] 赵冰，臧思宁，平义和，等.基于正交基函数的超宽带昹冲设计方法研究[J].黑龙江大学工程学报，2017，8(2)：76-79.

[12] 韩亚萍，吴江，曾凡达.飞秒激光作用下单晶硅表面载流子的超快动力学研究[J].黑龙江大学自然科学学报，2017，34(2)：224-228.

[13] Scouler W J. Temperature-modulated reflectance of gold from 2 to 10 eV [J]. Phys. Rev. Lett., 1967，18(12)：445-447.

[14] 邓素辉，陶向阳，刘明萍，等. 飞秒-纳秒脉冲激光烧蚀金属热效应分析[J]. 激光技术， 2007，31(1)：4-7.

[15] Vial A，Laroche T. Comparison of gold and silver dispersion laws suitable for FDTD simulations [J]. Applied Physics B-Lasers and Optics，2008，93：139-143.

[16] Etchegoin P G， Le Ru E C， Meyer M. An analytic model for the optical properties of gold [J]. The Journal of Chemical Physics，2006，125：164705-164707.

[17] Guo L，Xu X F，Salvador J R. Ultrafast carriers dynamics in filled-skutterudites [J]. Appl. Phys. Lett.， 2015，106(23)：231902-231905.

[18] Guo L，Xu X F. Ultrafast spectroscopy of electron-phonon coupling in gold [J]. Journal of Heat Transfer-Transactions of the ASME， 2014，136(12)：122401-122406.