切换系统线性二次最优控制:动态规划方法
2018-01-12吕东方毕永利
吕东方,毕永利,丛 屾
(黑龙江大学 机电工程学院,哈尔滨 150080)
切换系统是若干具有相似属性的子系统在切换信号驱动下构成的动力学系统,根据切换信号的规律与作用,可以将其归结为下述情形:①切换信号具有可操作性,可视作逻辑控制器;②切换信号不具有可操作性,但是其随时间的演化规律是确定已知的,例如满足周期性与遍历循环性;③切换信号具有任意性,其规律完全未知;④切换信号随时间的演化规律满足一定的统计规律,Markov跳变系统即为这类切换系统。
数字控制技术广泛应用使得具有逻辑属性的控制规律与作用的研究日益重要,作为一种特殊的逻辑控制器,切换控制的机理及其对于系统控制性能的影响成为近年控制理论界研究的热点问题。理论分析表明,对于时变参数系统,非线性系统等复杂系统,切换控制可以取得了良好的效果。
考虑将切换作为逻辑控制变量,通过与连续控制器的协同作用实现切换系统的线性二次最优控制。文献[1-2]考虑了自治切换系统的最优控制问题,子系统之间的切换通过状态空间中的超平面触发。文献[3]试图从更为一般的角度分析切换控制系统的基本理论,将其归纳入“混杂控制系统”的理论范畴中:自治与可控的切换现象均被视为一种特殊的“状态转移”,为从更为广义的观点研究切换控制提供了可能性。文献[4]将优化控制的方法应用于切换系统镇定问题,给出了平面切换系统可镇定的充分必要条件。文献[5]给出了离散时间下最优控制的一个必要条件。文献[6]考虑的逐段线性系统具有与之相似的运行机理,其最优控制问题局限于构造子系统的状态反馈控制器以实现特定的控制性能,而切换的优化功能未能得到体现。文献[7]通过弱化经典最优控制理论中的一些假设条件,将Pontryagin最大值原理推广至切换控制系统的理论框架内,描述了最优切换控制的若干基本属性。文献[8]给出了一个定义在Lie群上的最优时间控制存在的必要条件。文献[9]通过引入向量值函数与“切换障碍算子”,利用动态规划方法分析了切换控制系统的最优控制问题,并将最优切换策略的存在性判别与设计问题归结为一组非线性Hamilton-Jacobi-Bellman方程解的存在性判别问题,同时利用“变分不等方程”与“粘性解”刻画解的存在性及其性态;这些数学工具较为复杂,其结论的实用性不强。对于由两个子系统构成的切换系统,文献[10]将切换时刻作为“控制参数”,通过计算控制性能指标的对于切换时刻的变分的灵敏度及传统的优化计算方式给出最优切换时刻的设计算法。文献[11-12]包含了切换系统最优控制发展的更为详尽的介绍。
对于完整的控制系统而言,逻辑控制通常是较之于反馈控制单元更高层面上结构单元,承担整个系统的协调与整合的任务,因此其控制规律的设计,对于系统运行性能具有至关重要的作用。针对时变线性子系统,利用动态规划的基本方法与原理,给出了最优反馈控制与切换控制联合设计的过程,同时论证了这种最优控制对的存在性准则,并且给出了次优控制设计方案。
由于切换系统最优控制的复杂性,现有结果一般只能得到次优控制方案。相对于此,基于动态规划方法给出的反馈控制设计可以达到理论上的最优化;在最优控制方案不可行时,给出了一个较为易于实现的次优控制方案。
1 问题描述
由若干非线性子系统:
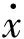
(1)
构成的切换控制系统描述如下:
s(t)=π(x(t),s(t-)),t≥0
(2)
其中x∈Rn,u∈Rm,s∈{1,…,N}分别为系统状态,连续控制输入及切换控制;从最优控制理论的角度出发,对于时变子系统:
fi:R+×Rn×Rm→Rn,i∈{1,…,N}
假设其对于各个变量具有一阶连续偏导数。
容许切换控制集与容许连续控制集分别定义如下:
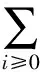
(3)
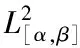
设yt,x(·)=yt,x(·,u(·),s(·))表示微分方程:
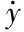
(4)
在初始条件(t,x),t≥0下的解。
对于指标i∈{1,…,N},其性能指标为可测函数:
Li:R+×Rn×Rm→R+
(5)
同时设h:Rn→R+为连续函数。
问题1 对于给定初始值x(0)=x0,是否存在最优控制对及相应的系统解{u(·),s(·),y0,x0(·)}使得性能指标:

(6)
达到最小值,并求出最优控制对及最优性能指标。
问题2 如果问题1的答案是否定的,那么寻求性能指标的次优解及相应的次优控制对。
注1 对于容许控制(3),微分方程满足所谓的Caratheodory条件,可以严格论证方程解的存在性,唯一性,以及对于初值的连续可微性,因此对于上述问题只要存在最优控制对(u(·),s(·))∈Ξ[t,T]×Ψ[t,T],则相应的系统最优解唯一确定。
2 初步结果
根据注1,利用动态规划的方法与基本原理分析问题1,为此引入值函数如下:

(7)
其边界条件V(T,x)=h(x)。下述定理是动态规划理论的主要理论体系。
定理1 值函数V(·,·)关于其自变量是连续的。
定理2 给定初始条件(t,x)∈[0,T]×Rn,对于∀θ∈[t,T],成立下述关系式:
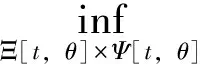
(8)
定理3 假定值函数具有一阶连续偏导数,那么其满足下列Hamilton-Jacobi-Bellman方程:
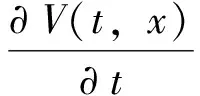
(9)
这里H:R+×Rn×Rm→R为Hamilton函数:

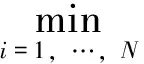
(10)
其中Hi(t,x,p),i∈{1,…,N}为相应子系统的Hamilton函数。
注2 对于比较特殊情形,比如线性二次最优控制问题,值函数(3)具有一阶连续偏导数;在一般情形下,值函数只满足连续性,因此HJB方程在经典意义下的解并不存在,为此需要在更为广泛的意义下讨论其解的存在性及相关性态(粘性解)。
3 主要结果
下面讨论切换系统线性二次最优控制问题,为此将分别考虑子系统为线性时变与线性时不变两种情形。
3.1 时变子系统的情形
时变线性切换系统描述如下:
s(τ)=π(x(τ),s(τ-)),τ≥0
(11)

考虑定义于有限区间[0,T]上的二次型性能指标:

(12)
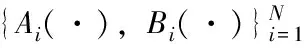
线性二次最优控制问题的值函数具有正定二次型的形式:

(13)
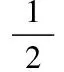
注3 对于切换线性控制系统,定义式(13)的值函数为连续逐段光滑函数,即其一阶偏导数几乎处处存在,并且逐段连续,因此其在经典意义下几乎处处满足HJB方程。
根据最优性原理(8),对于给定初始条件(0,x0)及任意指标i∈{1,…,N}与任意时刻0<θ (14) 注4 由此说明,合理的运用切换控制,可以达到较之于非切换控制系统更加优越性能指标。但是如果切换控制的运用不适当,则将恶化系统的控制性能。 下面论证切换系统线性二次最优控制的存在性、可解性以及最优控制对的构造。 对于每个子系统,在有限区间[0,T]上,由HJB方程导出的微分Riccati方程具有如下形式: τ∈[0,T],i∈{1,…,N} (15) 具有边界条件Pi(T)=KT,i∈{1,…,N}。 根据假设1,微分Riccati方程(15)存在有界正定解,并且具有一阶连续导数[4]。根据连续性,下述定义是有意义的: (16) 依据最优性原理,在末端区间[T1,T]上i1子系统可以实现性能指标的最小化。根据动态规划基本原理“全局最优解必定为局部最优解”,相应的连续反馈控制器设计为: (17) 从而,问题1可以归结为子区间[0,T1]上加以考虑。 类似地,对于每个子系统,在子区间[0,T1]上,由HJB方程导出的微分Riccati方程具有如下形式: τ∈[0,T1],i∈{1,…,N} (18) 具有边界条件Pi(T1)=Pi1(T1),i∈{1,…,N}。由此最优切换时刻确定如下: (19) 在末端区间[T2,T1]上i2子系统可以实现性能指标的最小化,相应的连续反馈控制器设计为: (20) 对于切换系统线性二次最优控制问题,重复上述过程,得到的最优控制对设计算法与构造方案。 算法1 ①在问题的原始区间[0,T]上,对于每个子系统,分别求解由HJB方程导出的具有边界条件的微分Riccati方程;②沿时间轴“逆向”比较微分Riccati方程的解,以确定切换时刻T1及最优的末端控制对;③将最优控制问题的定义区间缩小至[0,T1],并且根据②确定其边界条件;④重复②与③,并确定最优切换时刻及相应的最优控制对,直至上述过程到达零点。 依据(16,17;19,20;…),得到主要定理如下: (21) 注5 对于一维系统,由于存在自然序关系,因此算法1最终将到达零点,即一维切换系统线性二次最优控制问题存在最优控制对及相应的最优解。在高维状态空间中,由于缺少这种自然序关系,因此其最优控制对可能并不存在;在一般条件下,同时设计最优连续控制与切换控制未必可行。为此提出一种连续控制与切换控制分层独立构造的便于实现的次优控制方案。 (22) (23) 由此得到反馈闭环子系统: 切换控制设计为: (24) 较之于无切换控制的情形,在子系统反馈控制(23)与切换控制(24)作用下可以优化系统线性二次性能指标。 证明设由切换控制(24)所确定的切换序列如下: {(s(t0),t0),(s(t1),t1),…,(s(tM),tM):0=t0 (25) 对于线性二次性能指标,存在如下估计: (26) 结论得证。 注6 根据微分Riccati方程解的收敛性质,如果通过算法1构造最优控制对的条件成立,那么可知: (27) 因此,较之于定理7中构造的次优控制,定理6中构造的最优控制对可以得到更好的控制效果。但是定理7中次优控制不需要反复求解微分Riccati方程边值问题,因而更便于实现。 时变线性切换系统描述如下: s(τ)=π(x(τ),s(τ-)),τ≥0 (28) 考虑定义于无限区间[0,∞)上的二次型性能指标: (29) 为利用动态规划方法讨论相应的最优控制问题,引入以(29)为性能指标的值函数如下: (30) 由于在构造最优控制对时,不可能使切换无限次地进行下去,因此将无限时间区间上的最优控制问题转化为有限时间区间上的最优控制问题,但是其最优解可以任意地逼近原始问题的最优解。 定理6 给定初始值x0∈Rn及任意ε>0,存在T0(x0,ε)>0,使得(30)中定义的值函数满足如下估计: (31) 对于所有容许控制一致成立。 证明根据假设2,下列代数Riccati方程: (32) 注7 类似于时变子系统的情形,在无限区间上切换系统线性二次最优控制可以转化为有限区间[0,T0]上的最优控制问题,通过算法1重复计算一组微分Riccati边值问题,而得到最优控制对,其初始边界条件为PT0=0。 利用动态规划的基本原理与方法,分析切换系统线性二次最优控制问题的可行性,最优解的存在性,以及最优解的构造。通过“动态规划基本原理”实现了最优控制对存在性判别及其构造的算法,将其归结为一组微分Riccati方程边值问题的求解。论证了在一维情形下最优解的存在性,给出了连续控制与切换控制分层独立设计的次优控制方案。 [1] Anderson B D, Moore J B. Linear Optimal Control [M]. New York: Prentice-Hall, 1971. [2] Liu C, Gong Z. Optimal Control of Switched Systems Arising in Fermentation Processes [M]. Berlin: Springer, 2014. [3] Branicky M S, Borkar V S, Mitter S K. A unified framework for hybrid control: model and optimal control theory [J]. IEEE Trans. Automatic Control, 1998, 43(1): 31-45. [4] Cong S. Stabilising switching law to minimise return ratio with two linear planar subsystems [J]. International Journal of Control, 2014, 87(5): 976-986. [5] Hampel A B, Goulart P J, Lygeros J. Strong stationarity conditions for optimal control of hybrid systems [J]. IEEE Trans. Automatic Control, doi: 10.1109/TAC.2017.2668839. [6] Rantzer A, Johansson M. Piecewise linear quadratic optimal control [J]. IEEE Trans. Automatic Control, 2000, 45(4): 629-637. [7] Sussman H J. A maximum principle for hybrid optimal control problems [C]// Proc. of the 38th IEEE Conf. on Decision and Control. Piscataway, NJ: IEEE Press, 1999: 425-430. [8] Taringoo F, Caines P E. On the optimal control of hybrid systems on Lie Groups and the exponential gradient HMP algorithm [C]// Proc. of the 52nd IEEE Conf. on Decision and Control. Piscataway, NJ: IEEE Press, 2013: 2653-2658. [9] Yong J. The Dynamic Programming Approach and the Hamilton-Jacobi-Bellman Equations [M].Shanghai: Shanghai Scientific & Technical Publisher, 1992. [10] Xu X P, Antsaklis P J. Optimal control of switched system based on parameterization of the switching instants [J]. IEEE Trans. Automatic Control, 2004, 49(1): 2-16. [11] Zhu F, Antsaklis P J. Optimal control of hybrid switched systems: a brief survey [J]. Discrete Event Dynamical Systems, 2015, 25(3): 345-364. [12] 武国顺,陈良,魏永康,等.3-UPU并联机构运动学性能分析[J].黑龙江大学工程学报,2017,8(2):93-96.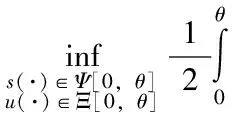




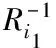


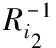










3.2 时不变子系统的情形





4 结 论
