基于地震属性差异的地层空间转换函数计算方法
2018-01-12范廷恩王宗俊张雨晴刘向南
聂 妍,范廷恩,王宗俊,张雨晴,刘向南
(中海油研究总院 开发研究院,北京 100028)
在油田开发阶段,地质模型的建立对部署井位,制定有效的开发方案和措施具有重要意义。基于地震数据的建模方法为重要的建模方法之一,前人已经有一些研究,如地震岩石物理建模方法[1],为模拟实际岩石弹性模量提供一个等效的介质模型。多层位约束的地震数据驱动建模方法,将地震解释得到的层位建立地层格架,在层位的约束下对该地层进行网格化,建立在多层位约束下的模型网格表征油藏模型格架。根据所建立的非均匀采样的模型网格,将地震数据和测井数据重采样之后离散化到模型网格里,分层位求取地层空间转换函数[2-4]。
地震数据是一个空间变化关系的数据载体,反映了地质体在空间上的变化。以地震信息为主体,以井信息为条件,基于地震信息本身所具有的确定的空间变化关系即空间转换函数,在已知空间转换函数的基础上推导出储层空间物性的变化特征,从而得出储层的物性参数数据,建立储层物性的高分辨率模型的确定性地质建模方法[5]。在已知地震数据的前提下,可得到它的空间变化特征,从而反推出地质储层的空间变化规律。地层空间转换函数代表了地震数据的空间变化特征,是地震信息驱动的确定性建模方法的核心[6-7]。因此,本文对如何基于地震属性差异求取地层空间转换函数开展了深入的研究。
1 基本原理
地震数据的变化反映了地质体在空间上的变化,在已知的石油或水资源井点位置,测井数据和地震数据反映的是同一地下情况,只是两者的数据形式不同。两者之间的转换关系可以用地层空间转换函数来表达。在已知地震数据和测井数据的前提下,可以得到地层空间转换函数,从而反推出未知点的地质储层的空间变化规律[8-10]。
若地震数据与测井数据相关性好,与测井数据的变化保持一致,则地震属性差异与测井数据差异也有一致性,即若待估点和井点地震属性差异性小,待估参数与井点参数差异也小,说明待估点和井点的物性较为相似,建模时此井的地层空间转换函数应给予较大值,反之亦然。
另外,由于反映地质体的地震属性和储层参数有很紧密的联系[11],因此储层状况的变化可以通过储层参数敏感的地震属性来分析[12],若能联合已知井可定量预测储层参数值。
假设已知有n口井,Li为已知井的物性参数值,Si为井旁道地震属性。Snew为待估点的地震属性,为了计算待估点的物性参数值Lnew,先根据地震属性差异求取各井地层空间转换函数φi,利用各井物性参数值权重ωi,计算待估点的物性参数值:
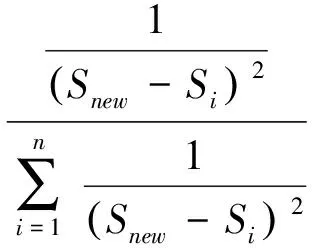
(1)
(2)
通过类似的迭代计算,可以计算出一系列物性参数值。基于地震属性差异的地层空间转换原理就基于此[13]。利用此算法计算的物性参数值与待估点地震属性差异较小的井点物性参数相近,从而建立的模型与地震属性的分布较为一致,便于后期分析实际的储层特征。
2 模型仿真与测试
对基于地震属性差异计算地层空间转换函数的可行性,根据实际数据建立一个二维模型进行试验。模型参数见表1。
模型主要有两个砂体组成,其余部分是泥岩,将砂泥岩的分界线作为层位进行约束,一共划分4个层位,并在层位的约束下进行模型网格化,建立了深度域的网格模型,模型的波阻抗分布见图1,孔隙度分布及井位分布见图2。
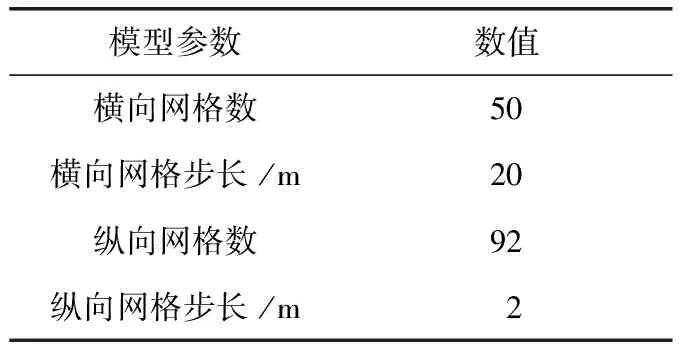
表1 模型参数

图1 模型波阻抗分布Fig.1 Map of impedance distribution
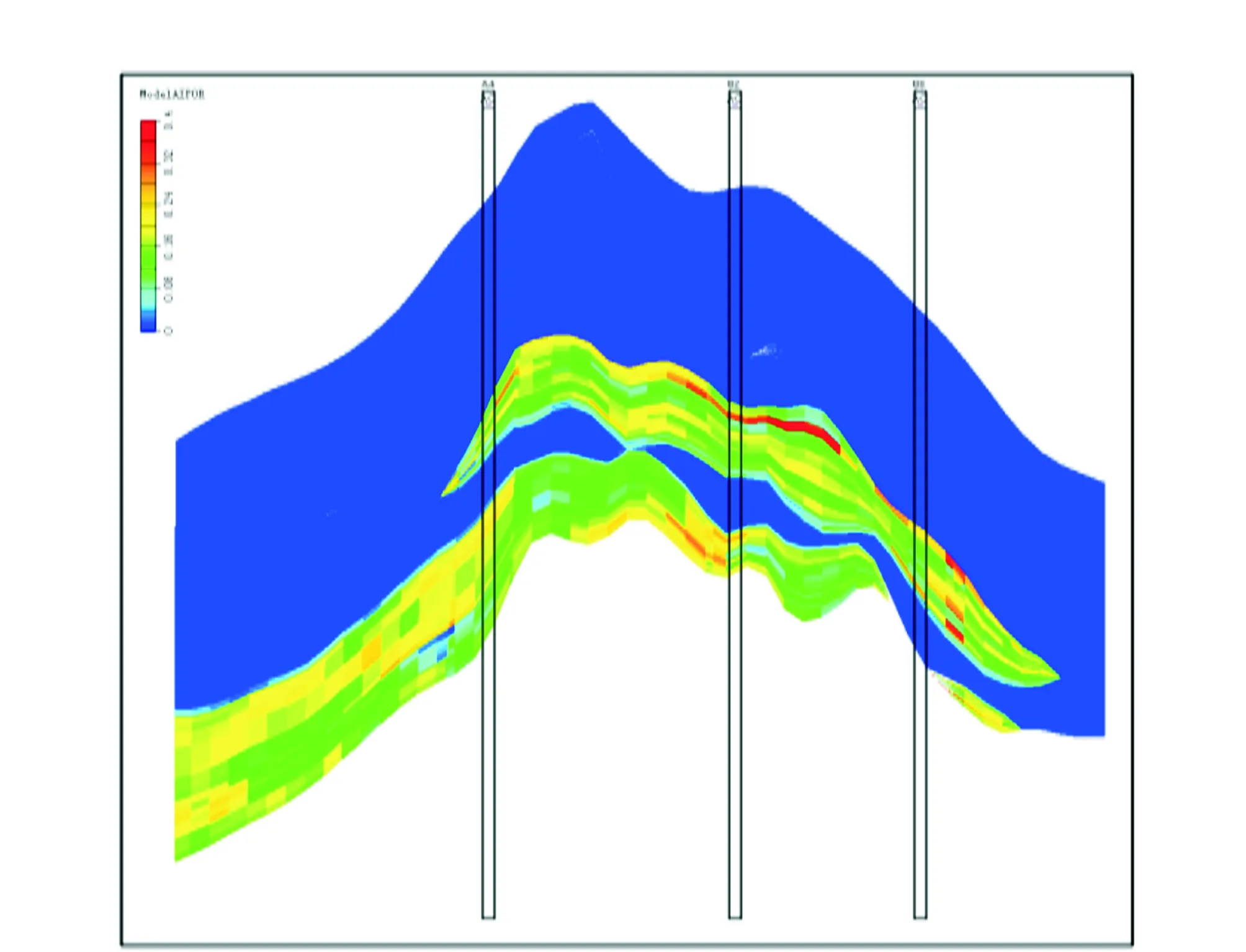
图2 模型孔隙度分布及井位分布Fig.2 Map of porosity distribution and well location
采用基于地震属性差异求取加权系数的方法计算地层空间转换函数,并通过建立孔隙度模型来检查方法的准确性。基于地震属性差异计算地层空间转换函数建立的孔隙度模型见图3。由图3可见,通过与图1和图2对比,采用本文提出的基于地震属性差异方法建立的孔隙度模型与在模型低孔隙度值的位置估计误差非常小。为了进一步分析所提方法的优越性,笔者从盲井检验分析。基于地震属性差异计算地层空间转换函数建立孔隙度模型的盲井检验方法见图4。由图4可见,与常规模型方法[11]比较,本方法建立的孔隙度模型更接近理论模型的孔隙度,精度更高。

图3 基于地震属性差异计算地层空间转换函数建立的孔隙度模型Fig.3 Porosity models obtaining by formation space conversion functions based on the difference of seismic attributes
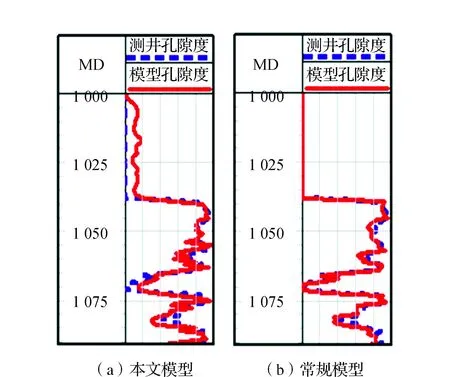
图4 地层空间转换函数建立孔隙度模型的盲井检验Fig.4 Blind wells check by formation space conversion functions
基于地震属性差异计算地层空间转换函数的误差分析见图5。由图5可见,误差控制在极小的范围内。其主要原因是基于地震属性差异的地层空间转换函数能更好地反映储层物性的变化,转换过程中引入误差更小,模型刻画精度更高,因此,基于地震属性差异的方法计算地层空间转换函数建立的孔隙度模型准确度较高。
3 实际应用与分析
通过以上的实验模型分析,基于地震属性差异计算地层空间转换具有较好的精度和准确度。笔者对Q油田进行实际应用开发分析。基于Q油田的实际资料,采用基于地震属性差异求取加权系数的方法计算地层空间转换函数,并建立孔隙度模型。Q油田应用地层空间转换函数建立的孔隙度模型见图6。

图5 基于地震属性差异计算地层空间转换函数误差分析Fig.5 Error analysis of formation space conversion based on the difference of seismic attributes

图6 基于地震属性差异计算地层空间转换函数建立的孔隙度模型Fig.6 Porosity model obtaining by formation space conversion functions
由图6可见,基于地震属性差异求取地层空间转换函数建立的模型孔隙度在砂体位置孔隙度值较高,孔隙度高值的分布较广,与测井孔隙度的分布一致。为了评价基于地震属性差异求取地层空间转换函数及建立的孔隙度模型是否合理、稳定,抽取评价井,利用评价井检验模型的合理性。建模过程中以A4井作为盲井,即A4井不参与建模,利用剩下的井建立孔隙度模型,再将在A4井处的模型孔隙度与A4井孔隙度进行对比,分析模型孔隙度与测井孔隙度的误差,据此评价该方法求取地层空间转换函数的精度。在A4井的井点处基于地震属性差异的模型孔隙度与A4井的测井孔隙度基本吻合,分辨率较高,证明该方法的建模效果较好。基于地震属性差异求取的地层空间转换函数分辨率较高,包含的信息比较丰富,说明该函数能够很好地表征物性参数的空间变化规律。
为了进一步量化分析地层空间转换的精度,对基于地震属性差异计算地层空间转换模型与实际对比,计算的误差见表2。误差变化曲线见图7。

表2 基于地震属性差异计算地层空间转换误差

图7 Q油田地层空间转换误差变化曲线Fig.7 Error variance of formation space conversion applied on Q oil field
由图7可见,基于地震属性差异计算地层空间转换误差能控制在一个很小的范围内。地层空间转变方法,可以推广应用于其它地质相关问题的研究中,如地下资源分析及地质灾害分析等[14-15]。
4 结 论
本文提出一种基于地震属性差异求取地层空间转变函数的方法。通过模型测试及实际应用证实,基于地震属性差异求取加权系数的方法计算地层空间转换函数建立的孔隙度模型精度较高,包含信息较丰富,其稳定性也较好,能较好地表征物性参数的空间变化规律。本方法作为地震信息驱动的确定性建模方法的核心,有效应用该转换函数可以更精确进行储层表征。在今后油田开发阶段的建模过程中,利用该方法计算地层空间转换函数,对地质建模意义重大。
[1] 张佳佳. 地震岩石物理建模方法及其在油页岩勘探中的应用[D]. 青岛:中国海洋大学, 2015.
[2] 马琳. 地震信息驱动的建模方法初探[D]. 东营:中国石油大学, 2010.
[3] 牟中海, 尹成. 地震地层学 [M]. 北京:石油工业出版社, 2013.
[4] 周建科, 印兴耀,曹丹平. 井震资料尺度匹配过程中声测井数据的精细分层方法研究[J]. 物探化探计算技术, 2015, 37(2):242-247.
[5] 乐靖. 多层位约束的地震数据驱动建模方法研究[D]. 东营:中国石油大学, 2011.
[6] 陈建阳,于兴河,李胜利. 多地震属性同位协同储集层地质建模方法[J]. 新疆石油地质, 2008,29(1):106-108.
[7] 左健扬. 地震驱动建模和地质统计学建模方法的比较和评价[D]. 东营:中国石油大学, 2011.
[8] 肖娟. 地震资料在三维地质建模中的应用[J]. 油气地球物理, 2011, 9(1):28-30.
[9] 李苗, 耿懿,李璇.地震约束降低储层建模中的不确定性—以委内瑞拉MPE3区块超重油油藏O-11a为目标层研究[J].西安石油大学学报:自然科学版, 2016,31(3):39-56.
[10] 张义, 尹艳树. 井震结合精细储层建模方法与实践[J]. 科技导报, 2015, 33(19):91-95.
[11] 刘伟, 尹成, 王敏,等. 河流相砂泥岩薄互层基本地震属性特征研究[J]. 石油物探, 2014, 53(4): 468-476.
[12] 张营革. 能量半衰时属性在浊积岩储层预测中的应用研究[J]. 石油物探, 2013, 52(6): 662-668.
[13] 乐靖, 王晖, 范廷恩,等. 基于地震等时格架的倾角导向储层静态建模方法[J]. 石油物探, 2017, 56(3): 449-458.
[14] 王思聪, 戴长雷, 张晓红,等. 不同视角的三江平原地下水资源量分析与评价[J]. 黑龙江大学工程学报, 2016, 7(4): 24-30.
[15] 石长金, 刘建新, 荆卉. 黑龙江省煤矿区地质灾害与防控措施研究[J]. 黑龙江水专学报, 2008,35(3):60-62.
