基于收敛性线性粒子群优化算法的1-SVM电力设备状态分析方法

2018-01-12林繁涛段永贤张建良齐冬莲

黑龙江大学工程学报 2017年4期

林繁涛，卢达，段永贤，张建良，齐冬莲，*

(1.中国电力科学研究院有限公司, 北京 100192;2．浙江大学电气工程学院, 杭州 310027)

随着电力系统数字化建设与信息化改造的进一步推进，电网设备状态的智能监控和有效分析成为实现电力系统智能化的迫切要求。由于新能源发电和微电网技术的快速发展和部署，电力系统尤其是配电网领域中电力二次设备的状态分析成为保证电网安全稳定运行的重要因素。

近年来，基于机器学习的电力设备状态分析技术发展极大地提升了通用物体的定位及识别能力,并逐渐应用于电力系统的安全可靠运行中，并取得了一系列的研究和应用成果。目前，电力系统设备状态的分析识别技术主要包括以特征匹配为特点的粗略分析方法[1-2]、以水平集为代表的精细分析法[3-4]和以支持向量机(Support Vector Machine，SVM)为代表的机器学习算法[5-6]。

在特征匹配方法方面，文献[1]基于尺度不变特征变换(SIFT)与霍夫(Hough)变换等算法，在变电站机器人上实现了断路器和各种隔离开关的位置状态的自动识别；文献[2]提出利用SURF算法对待测图像和数据库中的模板图像分别进行特征点检测并求出其描述子，通过特征点粗匹配与基于欧式距离的特征点精匹配实现对变电站开关分合状态识别。然而，以特征匹配的方法需要通过机器学习算法学习大量的训练样本才能生成目标模型，在训练样本数量较少的情况下识别效果不佳，同时计算量较大，结果受环境影响大。在水平集方法方面，文献[3]基于简化的Mumford-Sha水平集(Level Set)图像分割模型，提出一种紫外图像放电区域分割方法，可在不进行滤波预处理的情况下，有效地抑制泊松噪声和高斯噪声引起的干扰；文献[4]提出一种改进的Chan-Vese模型并采用二值函数代替距离函数初始化水平集函数，同时对Chan-Vese模型的梯度下降流提出改进，实现对含强噪声和边缘模糊的电力设备图像的有效分割。相比基于特征匹配的方法，基于水平集的方法可以有效地获取电力设备及边缘在内的精细状态信息，通过精确定位能够实现目标设备在整幅图像中的精确分割和连续跟踪，但是此类算法在处理目标设备出现形变和对齐问题上效果欠佳。支持向量机是建立在统计学习理论上的第一个成功算法，通过选择函数子集及子集中的判别函数，利用有限样本信息在模型复杂性和分类能力之间寻求最佳折衷，使得机器学习结果的实际风险达到最小，获得了较好的分类性能。单分类支持向量机(one-class Support Vector Machine，1-SVM)算法是对传统SVM算法的重要扩展，其中1-SVM将统计学习理论扩展到无指导学习领域，并在图像分析、模式识别和状态判断等领域得到了良好的应用[5-6]，然而在SVM方法中，支持向量模型中参数的选取是一个关键的问题，这对分类识别的结果有着至关重要的影响。

针对1-SVM在状态分类中存在的参数选取问题，本文提出基于粒子群优化算法(Particle Swarm Optimization，PSO)的一种扩展算法——线性粒子群优化算法(Linear Particle Swarm Optimization，LPSO)，该方法可以寻求1-SVM模型的最优参数[7-11]，以实现对目前电力系统中关键设备的运行状态进行分析和识别，并通过汇集电网运行和设备检测或监测数据，实现对采集的电力大数据进行系统的处理和分析，以有效降低值班人员的劳动强度，同时对电网运行进行进一步的诊断、优化和预测，从而为系统的安全稳定有效运行提供技术支持和保障。

1 基于收敛性线性粒子群优化算法的1-SVM学习方法

针对传统1-SVM模型在电力设备状态分类中的参数选择问题，提出基于粒子群优化算法的一种扩展算法——线性粒子群优化算法，应用到单分类支持向量机的训练模型中；同时，针对粒子群优化算法中固有的收敛性和最优性问题，通过改变全局最优粒子的运动轨迹，解决了LPSO中存在的过早收敛和局部最优现象，该方法称之为收敛性粒子群优化算法(Convergent Linear Particle Swarm Optimization，CLPSO)[5-6,10-12]。因此，CLPSO在训练1-SVM模型用来状态分类时具有明显优越性。

1.1 线性粒子群优化算法

粒子群优化算法是对每一个粒子的每一个维进行速度和位置的更新:

(1)

(2)

而线性粒子群优化算法是通过以下的公式对每一个粒子所有维进行更新：

(3)

(4)

其中，相同的随机数r1和r2被应用到更新每一个速度向量。线性粒子群优化算法要求粒子的初始速度为0，且粒子的初始位置满足约束条件AP=b，其中A为矩阵，b为向量，即通过向量的线性关系定义粒子的运动轨迹。

1.2 收敛性线性粒子群优化算法

为了避免粒子运行到群体最优而陷入停滞状态，避免算法限于局部最优而过早收敛的问题，需要改变群体最优粒子的速度更新方式。设τ是当前整体最优粒子的指标，则:

pbestτ=pg

(5)

则群体最优粒子τ的速度更新方程变为:

(6)

其中，ρt为收缩系数，ϑt∈UNIF(-1,1)n是区间(-1,1)上均匀分布的随机数，并且满足Aϑt=0，即υ(t)在矩阵A的零空间中。因此:

(7)

群体最优离子的新位置是其个体最优位置与一个随机向量的和值。仅群体最优粒子通过以上的方式更新，其他所有粒子的速度和位置更新方式不改变。

1.3 基于收敛线性粒子群优化算法的1-SVM学习方法

针对单分类支持向量机的对偶优化问题，支持向量的系数需要被求解出来。粒子可以编码为p=(α1,…，αn)，适应度函数选取为:

(8)

因此，求解1-SVM模型中的系数选取问题，本质上是一个具有线性约束条件的二次规划问题。利用收敛性线性粒子群优化算法优化1-SVM，粒子的位置必须满足1-SVM的约束条件:

(9)

因此，在每一步迭代中需要调整粒子运动后的位置，具体方法见算法1。

算法1粒子位置的调整算法：

delta=d-1;

while|delta|>ε

{ifdelta>ε

{s=delta/n;

ifpin+s0

{pij=pij-s;}

}

else

{s=-delta/n;

ifpij-s0

{pij=pij-s;}

}

delta=d-1;

}

具体做法为：利用收敛性线性粒子群优化算法实现1-SVM的参数选取，详细步骤如下：

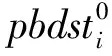
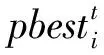
利用CLPSO实现1-SVM模型的参数选择，改变了群体最优的粒子位置变化方式，避免了粒子仅仅在群体最优位置附近运动的缺陷，促使粒子在附近领域搜索最佳位置。因此，CLPSO至少能够保证找到一个领域内的最优值，即CLPSO优于LPSO。

2 基于收敛性线性粒子群优化算法的1-SVM电力设备状态分析方法

在充分借鉴国内外现有研究成果的基础上，综合运用计算机视觉、机器学习、信息处理技术等领域的相关理论和技术，采用理论分析和实验研究相结合的方法，根据电力系统中关键设备(主要指隔离开关等)的状态分析类工程项目实施经验，提出包括模型学习、设备粗定位及对齐分割在内的电力设备状态识别主要技术框架，同时利用基于收敛性线性粒子群优化算法实现1-SVM分类模型中参数的选取，完成对电力设备状态精确对齐及分割，解决相应的关键技术和系统集成等问题。

图1 系统整体流程Fig.1 Flowchart of the designed system

本文提出的主要技术框架分为3大部分，分别为模型学习、设备粗定位及对齐分割，见图1。其中，模型学习对输入的几组表征不同开关状态的图像进行前期学习；开关定位部分主要利用模型中的特征匹配并应用广义Hough变换对开关设备进行粗定位；对齐分割部分应用本文基于收敛性线性粒子群优化算法的1-SVM方法，根据模型中的形状约束、颜色约束和前期粗定位获得的空间约束综合完成精确对齐及分割过程；最后通过精确对齐的结果即可分析出当前开关的状态信息。

2.1 模型学习

对于某一特定类型的开关设备(图2(a))，假定可以获得一组由原始设备为基础，并由较少图像构成的扩充模板图像样本组(图2(b))中3个灰度图像。其中的每张图像提供了不同状态下的开关形态，通过对这组图像进行模板图像的扩充，即对少量的样本组进行变换生成丰富的训练样本，为模型的进一步学习过程做好准备。然后，对于包含特定开关设备的前景图像部分，在每个学习样本上提取局部特征点，由于变换算法已知，通过计算相同特征点的方差，即可计算出每个特征点的稳定性匹配概率，该概率用于改善下一步的Hough投票过程，其中不稳定的特征点被直接剔除以降低系统计算量；对于背景图像部分，考虑综合利用颜色直方图和水平集方法提取开关所在图像的轮廓图像特征和直方图特征，以便进行进一步的分割处理，具体见图3。

图2 模板图像的扩充Fig.2 Expansion for template images

2.2 开关定位

在开关定位过程中，通过对全图部分进行密集特征点提取来获得特征点集合，见图4，并将该集合与模型组扩充图像特征点集合进行匹配。使用匹配相似度和模型组特征的稳定性概率进行定位投票，利用广义Hough变换获得多组目标区域，具体流程见图5。

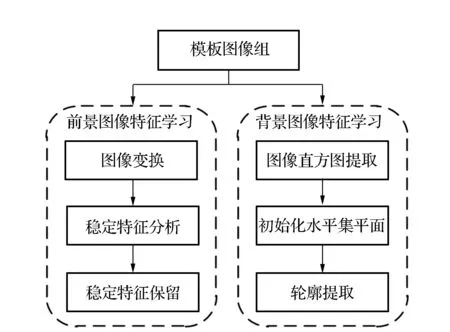
图3 模型学习过程Fig.3 Learning process for the image model

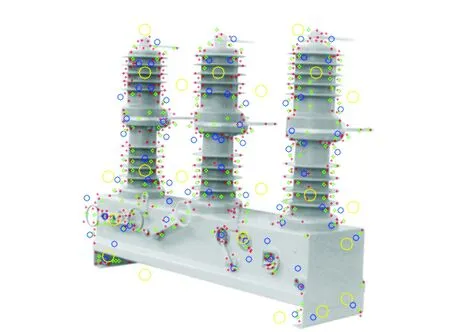
图4 稳定特征点提取Fig.4 Extraction of stable feature points

2.3 对齐分割

通过模型学习阶段(图3)提取开关的轮廓特征和颜色直方图特征，在对齐分割阶段，将位置区域特征、轮廓特征和颜色直方图特征组成的特征向量映射到1-SVM中的初始分类平面上。通过基于几何特征实现对原图像(图6)的粗定位结果(图7)，获得矩形框初始化仿射变换矩阵，利用基于收敛性线性粒子群优化算法的移动1-SVM中的分类平面，实现最优分类参数的选取，以获得最终的精确对齐及分割结果。具体的对齐分割流程见图8。

图5 开关定位过程Fig.5 Location process for disconnecting switches

图6 实拍原物Fig.6 Original picture

图7 粗定位结果Fig.7 Result of coarse location

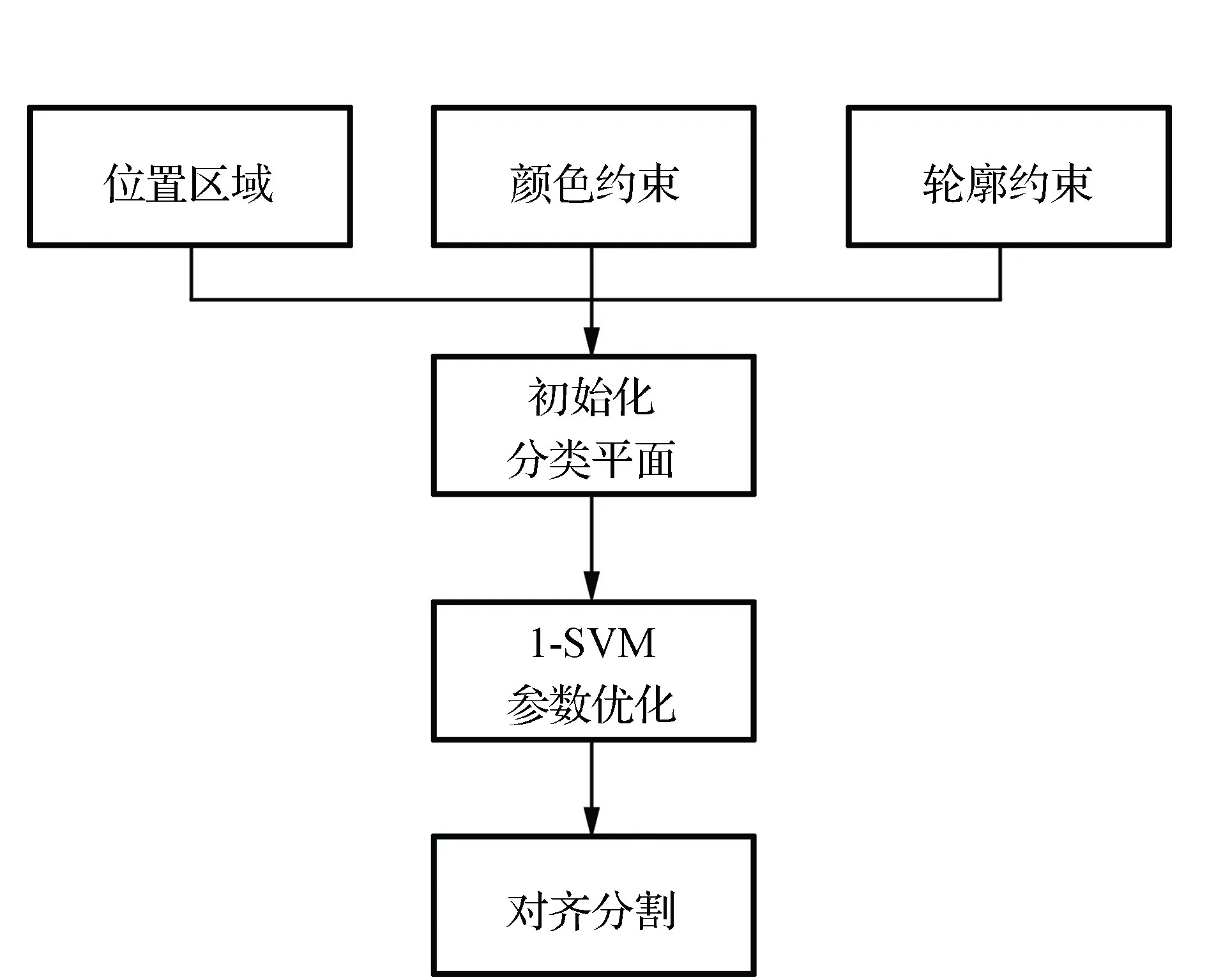
图8 对齐分割流程Fig.8 Process of alignment and segmentation

3 仿真实验

为了验证本文所提出方法针对电力系统设备状态分析的有效性，同时考虑到研究对象的重要性和代表性，仿真实验中的数据集对象选取来自在电力系统中占重要地位的变电站隔离开关，以此为主要对象对本文的方法进行进一步的验证分析。选取数据集是在不同环境下变电站隔离开关的图像数据集(图9)。

为了方便比较单分类支持向量机学习方法，实验统一选取核函数为高斯核函数:

K(xi,xj)=exp(-‖xi-xj‖2/σ2)

定义进行比较的分类算法正确率(Correct Rate，CR)为：

CR=correctlyclassified/TotalTesting

选取1-SVM的参数C=1，核函数参数σ=0.1。CLPSO的参数选取c1=2.8，c2=1.3，c=c1+c2=4.1，Vmax=0.5，Vmin=-0.5。此外，选取群体规模为s=50。

将CLPSO与基于序列最小化优化算法(Sequential minimal optimization，SMO)[13-14]和LPSO[15]的1-SVM模型学习方法的实验结果进行比较。

实验结果见表1，其中CLPSO能够得到与SVM的理想算法SMO相似的分类准确率，而比LPSO优越。LPSO使用了最少的支持向量，但是分类准确率最差，这也证明了LPSO容易陷入局部最优解，因此LPSO对精度要求高的分类问题并不适合。CLPSO避免了LPSO的缺陷，使用了较多的支持向量，提高了分类精度，而且训练时间并没有增加，提高了效率。CLPSO与SMO方法相比，分类精度优越性不明显，训练时间略有提高，但是却使用了少量的支持向量。对于SVM而言，少量的支持向量表示分类决策函数的复杂程度低，能够节省存储空间和降低计算量。出现这种情况的主要原因在于SMO需要复杂的分解机制和解决子问题的数值QP优化算法，随着分解步骤的增加，支持向量的个数也会随之增加。总之，本文提出的CLPSO方法是可行的，并且比SMO训练1-SVM更具有优越性。基于本文提出的CLPSO方法，针对图9的数据集对象，相应的隔离开关开关定位识别结果见图10。

表1 隔离开关图像数据集实验结果比较

图9 变电站隔离开关数据集Fig.9 Tested dataset of disconnecting switches in substation

图10 基于本文方法的隔离开关数据集分析定位结果Fig.10 Analysis and location results for disconnectingswitches by using the proposed method

4 结论

针对目前电力系统中关键设备运行状态的分析问题，提出了包括模型学习、设备粗定位及对齐分割在内的设备状态分析基本技术框架，同时提出了基于收敛性线性粒子群优化算法，解决了1-SVM学习方法在状态分类中的参数选取问题，实现对齐分割过程中准确性和快速性的良好平衡。通过仿真实验可见，提出的方法在以隔离开关为对象的设备分类识别中能够获得较快的处理速度，同时具备较好的分类性能。

[1] 陈安伟, 乐全明, 张宗益,等. 基于机器人的变电站开关状态图像识别方法[J]. 电力系统自动化, 2012, 36(6):101-105.

[2] 杨艳召, 王建平, 王库,等. 一种基于SURF的变电站开关分合仪表识别算法[J]. 自动化应用, 2015(8):21-23.

[3] 律方成, 马国明, 刘云鹏,等. 基于水平集模型的电气设备紫外图像放电区域分割[J]. 中国电机工程学报, 2008, 28(19):20-24.

[4] 顾鹏程, 黄福珍. 基于改进Chan-Vese模型的电力设备红外图像分割[J]. 计算机工程与应用, 2017(10):193-196.

[5] 王洪波. 单分类支持向量机的学习方法研究[D]. 杭州：浙江大学, 2012.

[6] Gu H, Zhao G, Zhang J. MMSVC: An efficient unsupervised learning approach for large-scale datasets[J]. Neurocomputing, 2012, 98(18):114-122.

[7] 陆宁, 武本令, 刘颖. 基于自适应粒子群优化的SVM模型在负荷预测中的应用[J]. 电力系统保护与控制, 2011, 39(15):43-46.

[8] 李磊, 高雷阜, 赵世杰. 基于神经网络的粒子群算法优化SVM参数问题[J]. 计算机工程与应用, 2015, 51(4):162-164.

[9] 韦忠善, 明鑫. 改进粒子群算法选择特征和神经网络参数的模拟电路故障诊断[J]. 内蒙古师大学报：自然汉文版, 2016, 45(1):55-59.

[10] 徐磊, 赵光宙, 顾弘. 基于作用集的一类支持向量机递推式训练算法[J]. 浙江大学学报：工学版, 2009, 43(1):42-46.

[11] 徐磊, 赵光宙, 顾弘,等. 成对耦合分类器的多球体预处理方法[J]. 浙江大学学报：工学版, 2010, 44(2):237-242.

[12] 杨帆，于鸣，李丹，等.基于粒子群算法优化BP神经网络的CO2通量预测[J].黑龙江大学自然科学学报，2017，34(4)：481-485.