气流激振压电发电机振动频率实验分析与估算

，，

(1. 常州机电职业技术学院机械工程学院，江苏 常州 213164；2.南京理工大学机械工程学院，江苏 南京 210094)

0 引言

引信用小型气流激振压电发电机是一种利用基于喷嘴-共振腔结构的气流致声激振机构，将弹丸飞行过程中的迎面气流转化为稳定声源，激励压电发电装置振动而产生电能输出的振动式压电发电机，该发电机具有结构简单、体积小、振动频率高且没有活动部件等特点，适合小口径引信弹载物理电源[1-2]。对于振动压电换能器来说：1)根据“频率泵浦”设计思想[3]，较高振动激励频率，有利于提高输出功率；2)为了最大限度地输出电能，设计时应该使激振力的频率与压电发电装置的固有频率较接近。因此，对气流激振压电发电机的振动频率进行研究具有重要的意义。

相关研究表明[4-7]，这类气流激振压电发电机的振动频率与激振力频率一致，且被共振腔声模态频率所俘获，也称之为共振腔的共振频率。因流声固耦合系统的振动模型复杂，至今还没有描述其耦合作用的精确数学表达式，所以，共振腔共振频率的计算一直是引用各种经验公式。Cain等[8]通过对哈特曼共振腔共振频率研究发现频率受喷嘴总压和喷嘴出口与共振腔口部的间距影响不大，其主要影响因素是共振腔长度，提出了基于共振腔长度的频率计算式。Kastner等[9]发现共振频率不仅与共振腔长度有关，还应考虑射流马赫数以及间距对近场和远场声压的功率谱的影响，于是修正了频率计算式。A. Hamed等[10]提出了考虑结构几何尺寸对不稳定流场特性以及质量流率的影响的频率修正计算式。国内，也有学者研究了共振腔长度、喷距、流压、喷腔直径等参数对频率的影响[11]，通过实验对哈特曼谐振管共振频率决定因素进行了研究，并对频率理论公式进行了修正[12]。

但是以上文献中所涉及的共振频率修正公式都是针对长共振腔的,而其用于短共振腔时，估算不准确(偏低)，因此，需要修正得到适合短共振腔的共振频率估算公式。本文针对此问题，提出了气流激振压电发电机振动频率实验分析与估算方法。

1 气流激振压电发电机工作原理

图1所示为气流激振压电发电机的结构示意图，由气流致声激振机构和压电换能器所组成。气流致声激振机构主要由环形喷口及共振腔(压电换能器封闭末端)组成，其中，环形喷口是由进气道和阻塞构成。喷注是弹丸飞行时的迎面气流(即入流)经喷口后得到的稳定涡流，喷注遇到共振腔口部的边棱(尖劈)产生扰动而形成边棱音[13]。由喷口发出的高速喷注在空腔内(共振腔前端)静止的空气中通过时，喷注的边界上因高速流与静止介质的接触，不断产生旋涡，并向前推动，因而喷注不断变宽，一部分遇到共振腔口部(边棱)时发生反射回到喷口，激发更多旋涡；一部分进入共振腔内激发其腔体振动，并在底部(刚性底部)反射回喷口。在声源处(共振腔口部)同时存在正、负向声波，如果它们同相则振动加强，即在共振腔内形成驻波，可以产生频率主要由共振腔长度决定的声波，共振腔底部声压最大(压力波的波腹)[4]。共振腔底部声压(即激振力)驱动压电换能器振动，输出电能，实现声能到电能的转换。

2 振动频率测量系统及实验装置

模拟弹丸飞行环境时，忽略了温度、湿度以及来流等因素的影响，仅模拟了管内流的压力或速度环境。实验系统主要由气源模拟系统、压力测量系统及实验试件等组成，如图2所示。气源模拟系统主要由气罐、减压阀和流量计组成，用于测量流速。压力测量系统主要由压力传感器和数据记录仪组成，用于测量共振腔底部M处声压(见图1所示)，经频谱分析后得到振动频率。

图3所示为实验照片。实验时，打开气罐，通过减压阀来调节进气口的气流大小，并通过流量计监测流量值；气流进入试件后，用压力传感器测量共振腔底部M处的声压(激振力)，并用数据记录仪对相应数据进行记录。然后，对声压曲线进行频谱分析就可得到激振力频率。

实验所选取的气源流量范围为100～300 L/min，对应试件入口处的气流速度V与流量Q之间的表达式为：

V=Q/S

(1)

式中，V为气流速度，Q为流量，S为截面积。

3 振动频率影响分析

本文在进行小型气流激振压电发电机振动频率影响分析时，主要考虑轴向2个结构参数，而不考虑尖劈角度大小，共振腔的壁厚、直径以及环形喷口大小，如图1所示。结构参数包括：1)共振腔长度L；2)共振腔直径D；3)间距X，即环形喷口到共振腔的距离；4)环隙H，即环形喷口的大小。本文中将共振腔直径与环隙喷口作为定值，即D=10 mm，H=1 mm，轴向结构参数L和X作为可变值。

3.1 共振腔长度对振动频率影响

分析共振腔长度对频率的影响时，分别选取L=8, 10, 15, 20, 30, 40, 50, 60 mm；X=3 mm；V=100 m/s。当长度为15 mm时，共振腔底部M处的声压曲线分别如图4所示。可以看出，声压曲线比较规律，近似正弦周期变化；频谱分析可知，频率峰值比较突出(约4.55 kHz)，说明声压的频率比较单一(基频)，不存在高阶频率的影响。因不同长度下所得到的曲线规律是一致的，故选取了代表性一组曲线，其他组用表列出数值，见表1所示。图5所示为振动频率与长度的关系，频率随着长度的增大而变小，且呈反比关系。

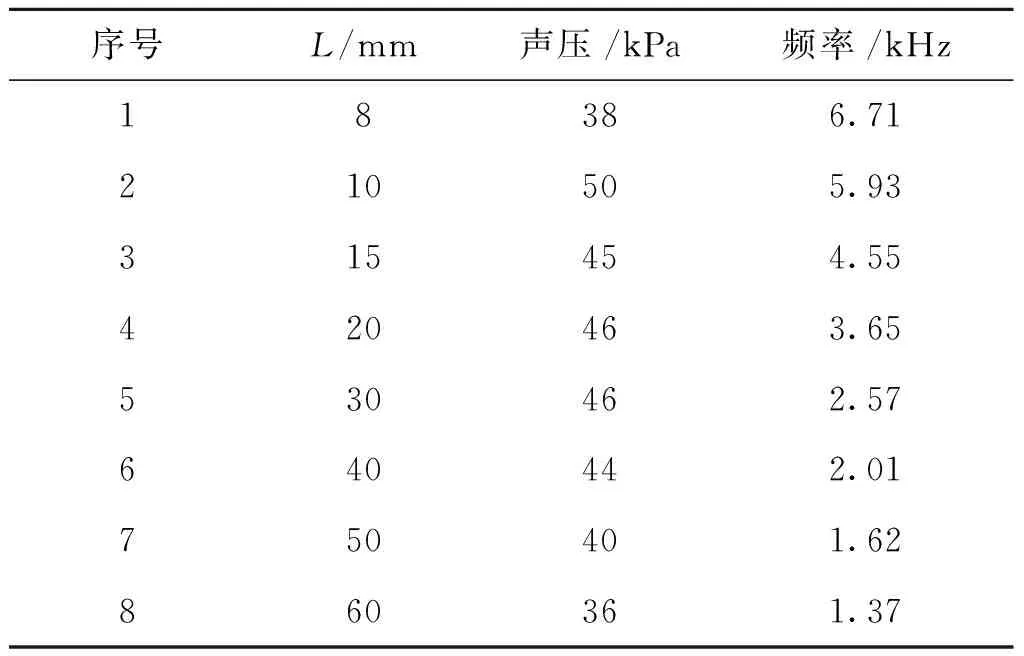
序号L/mm声压/kPa频率/kHz18386.71210505.93315454.55420463.65530462.57640442.01750401.62860361.37

3.2 间距对振动频率影响

分析间距对振动频率的影响时，分别选取L=10 mm；X=2，2.5，3，3.5，4 mm；V=100 m/s。当间距为3 mm时，共振腔底部M处的声压曲线分别如图6所示。其曲线变化规律与图4所示一致。因不同间距下所得到的曲线规律是一致的，故选取了代表性一组曲线，其他组用表列出数值，见表2所示。图7所示为振动频率与间距的关系，频率随着间距的增大而稍微变小。

序号X/mm声压/kPa频率/kHz12406.0522.5456.0133505.9443.5485.8554445.56

4 频率经验公式

根据以上分析结果可知，振动频率f随着共振腔长度L的增大而变小，呈反比关系，且随着间距X的增大而稍微变小，这与文献[14]中关于结构参数对共振腔共振频率的影响趋势是一致的。关于共振腔共振频率的理论公式有如下几种：

1)仅考虑共振腔长度的表达式[8]：

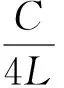
(2)

2)修正共振腔长度后的表达式[12]：

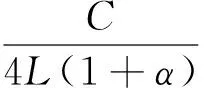
(3)

其中，α的取值范围为1.59%～3.2%。

3)修正共振腔开口端表达式[13]：

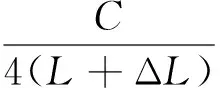
(4)

其中，ΔL为管开端口部的修正长度，ΔL=0.61R，R为共振腔的内径。

从以上3个公式可以看出，频率经验公式没有考虑到间距的影响，本文根据第3部分中关于频率与长度以及间距关系的研究结果，提出了如下的频率表达式：

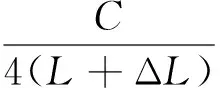
(5)

其中，ΔL=0.61R+αX，α约为0.4。

下面针对式(2)—式(5)所对应的频率理论值与实验值进行比较分析，验证本文所提出的频率表达式的有效性。

图8为频率与共振腔长度的关系，当长度相对较大(L=40, 50, 60 mm)时，不同公式所对应的频率理论值与实验值相差不大；但当长度相对较小(L=8, 10 mm)时，不同公式所对应的频率理论值与实验值相差较大；且长度越小，差距越大。

表3中对长度相对较小(L=8, 10 mm)时的频率理论值与实验值进行了比较，可以看出，长度L=10 mm时，式(2)的最大相对误差达43.33%，式(3)的相对误差为38.78%，式(4)的相对误差为9.78%，式(5)所对应的相对误差仅为0.51%。

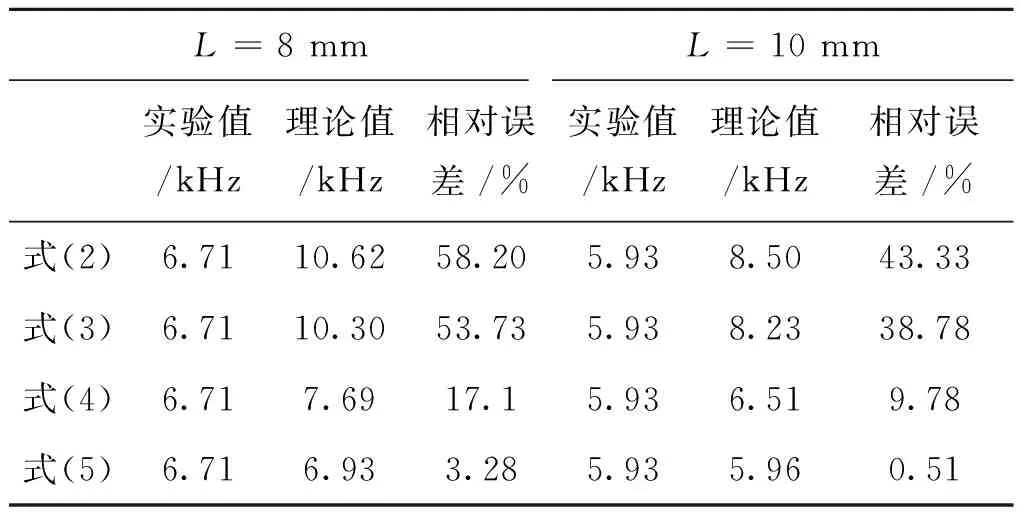
表3 长度较小时，频率理论值与实验值Tab.3 Theoretical value and experimental value of frequency under short resonator

另外，在不同长度下，式(5)所对应的共振频率理论值与实验值比较接近，其相对误差都在4.0%内，见表4所示。

表5为长度L=15 mm时，不同间距所对应的共振频率理论值与实验值。可以看出，式(2)—式(4)所对应的理论值与实验值的差距较大，式(5)所对应的理论值与实验值的差距最小。其中，式(2)的最大相对误差达35%，式(4)的最小相对误差也有5.4%，式(5)所对应的相对误差在1.1%内。

5 结论

本文提出了气流激振压电发电机振动频率实验分析与估算方法。该方法修正了现有频率表达式，适用于短共振腔的振动频率估算。结果表明，共振腔长度是影响频率的主要因素，随长度的增大而变小，且呈反比关系；间距对频率的影响不大，随间距的增大而稍微变小；修正后的频率经验公式理论值与实验值之间的误差较小，可作为估算振动频率的有效方法。为获得6 kHz以上高频稳定振动信号，可选择共振腔长度为8～10 mm以及喷口距共振腔距离不大于3 mm。因此，本文所得结论可作为设计振动频率的参考依据，从而确定关键结构参数。

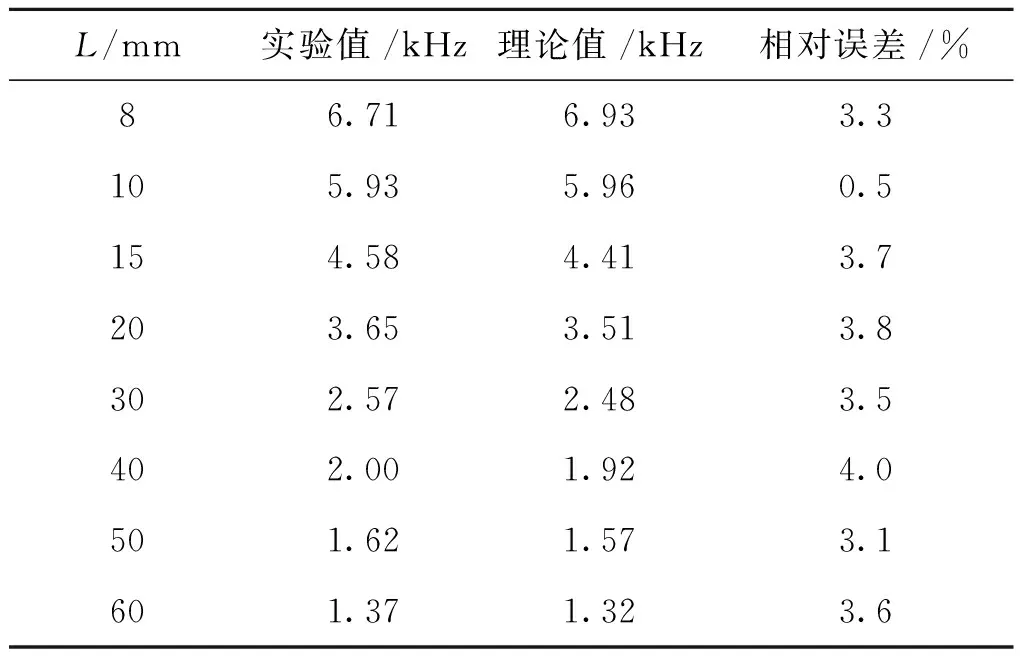
表4 不同长度下，式(5)理论值与实验值Tab.4 Theoretical value related to formula (5) and experimental value under different length

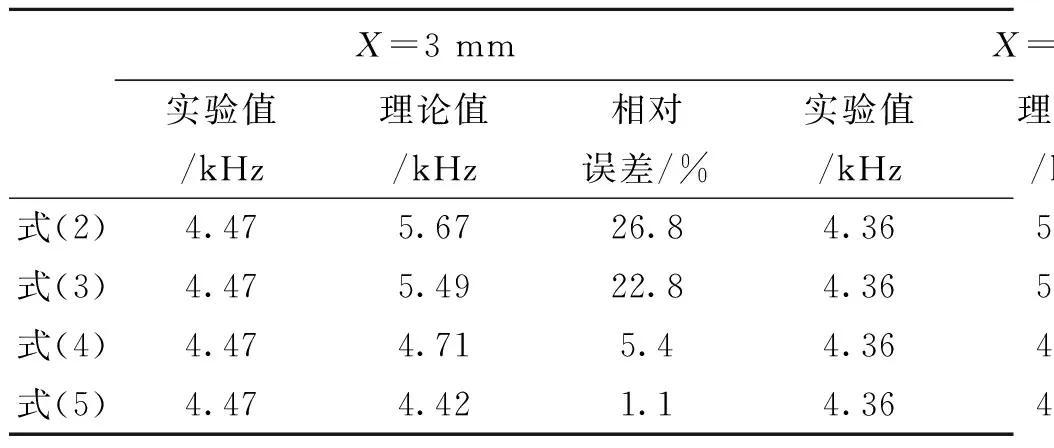
表5 不同间距下，频率理论值与实验值的相对误差Tab.5 The relative error between theoretical value and experimental value under different space

[1]李映平.引信压电发电机原理及试验研究[D].南京：南京理工大学，2006.

[2]Zou Huajie, Chen Hejuan, Zhu Xiaoguang. Piezoelectric energy harvesting from vibration induced by jet-resonator system[J]. Mechatronics, 2015, 26(2): 29-35.

[3] Priya S, Inman D J. Energy Harvesting Technologies[M]. Springer, 2009: 26-27.

[4] 邹华杰，陈荷娟，梁医.引信振动压电发电机气流致声振源特性研究[J].兵工学报，2015, 36(4)：610-618.

[5] Sun Daming, Xu Ya. A mean flow acoustic engine capable of wind energy harvesting[J]. Energy Convers Manage 2012, 63: 101-105.

[6] Wang DungAn, Chiu ChunYuan, Pham HuyTuan. Electromagnetic energy harvesting from vibrations induced by karman vortex street[J]. Mechatronics, 2012, 22: 746-756.

[7] Hernandez R, Jung S, Matveev KI. Acoustic energy harvesting from vortex-induced tonal sound in a baffled pipe[J]. J Mech Eng, 2011, 225: 1847-1850.

[8] Cain A B, Kerschen E J. Simulation of power resonance tubes-Effects of pressure ratio and freestream flow[J]. AIAA, 2002:2816-2821.

[9] Kastner Jeff, Samimy Mo. Development and characterization of Hartmann tube base fluidic actuators for high speed flow control[J]. AIAA,2002,40(10):1926-1934.

[10]Hamed A, Das K, Basu D. Numerical simulation and parametric study of a Hartmann springer tube based powered device[J]. AIAA, 2002:2003-2005.

[11] 路斌. 哈特曼声波发声器声学传播特性及应用研究[J]. 石油大学学报，2004, 28(6): 123-125.

[12] 张利杰，田章福，曾新吾. 哈特曼谐振管共振频率决定因素分析[J]. 声学技术，2008, 27(5)：212-213.

[13] 马大猷. 声学手册[M]. 北京：科学出版社，2004.

[14]ZOU Huajie, CHEN Hejuan, ZHU Xiaoguang. Characterization of acoustic excited power resonance tube for on-board piezoelectric generator [C]// 5thICMEM. Science Press USA Inc.,2014:589-594.