有源压制式干扰对MIMO引信测距测速的影响
2018-01-12,,,
,,,
(南京理工大学电子工程与光电技术学院,江苏 南京 210094)
0 引言
多发多收(MIMO)理念的提出有效改善了现代雷达的性能,而MIMO引信是一种基于MIMO理论的新型引信,是传统的无线电引信与MIMO理论相结合的产物。由于近几年干扰技术的逐步发展,MIMO引信测距测速等性能面临各种挑战,其中有源压制式干扰是应用极为广泛的一类干扰信号。有源压制式干扰通过发射高功率随机信号,在时域、频域及变换域上掩盖目标回波,破坏引信信息获取能力[1]。国内外学者对压制式干扰研究主要集中在压制式干扰抑制算法上,主要包括匹配滤波、动目标显示、自适应滤波、分形特征估计等[2-4]。基于相位编MIMO引信是近几年提出的新型体制MIMO引信,采用发射脉冲间相互正交或准正交的随机相位信号,具有良好的抗干扰性能[5-9]。本文针对目前对相位编码MIMO引信抗干扰分析不足的现状,分析了有源压制式干扰对基于相位编码的MIMO引信测距测速的影响。
1 MIMO引信测距测速算法
基于相位编码的MIMO引信发射信号间相互正交,MIMO引信接收端的信号都是各个通道的合成信号,因此需要将合成信号一一分离出来,因此MIMO引信将N个接收通道得到的回波信号与M个发射信号进行匹配,共得到M×N路匹配输出,这样就可以将不同发射信号所贡献的回波成分分离。根据阵元间相位差,对每个发射阵元和接收阵元的输出进行移相并加权求和,实现发射波束和接收波束形成。在匹配滤波和DBF后,需要对每个波束输出信号进行目标检测与参数估计。其信号处理流程与普通相控阵雷达的处理流程是类似的,经过多脉冲积累,然后经过动目标显示(MTI)、动目标检测(MTD)和恒虚警处理(CFAR)[10-12],根据匹配输出和MTD输出峰值位置可实现测距测速估算。
1.1 MIMO引信匹配滤波测距算法
设第n个接收阵元接收到的回波信号数学表达式为:
xn(t)=ae-j(n-1)φaT(θ)S(t)+Z(t)
(1)
发射信号相互正交,即:
(2)
式中,T为脉冲宽度,c为常数。
将该接收阵元接收的回波信号xn(t)与第i个发射阵元的发射信号si(t)作匹配滤波,匹配输出可表示为:
(3)
(4)
写成向量形式可以表示成:
Fn=a·e-j(n-1)φ·a(θ)·c+Un
(5)
所有接收阵元进行匹配滤波后,输出可表示成:
(6)
共M×N路输出,根据匹配后的波形的峰值可以算出延迟时间,估算出目标距离。
1.2 MIMO引信动目标显示测速算法
MIMO引信检测目标通常是运动目标,周围环境不可预料,各种干扰与回波混合给目标探测带来很大障碍,需要采取措施滤除回波中的某些杂波。通过MTI对消,将同一距离单元在相邻周期内的相检输出做相减运算,则固定目标回波将完全对消,慢杂波会得到大幅度抑制,仅有运动目标回波会被保留,故采用相邻脉冲相减就能滤除固定杂波。单脉冲对消器的幅频响应在零频附近的零值区间可能达不到要求,故采用双脉冲对消器,如图1所示。输出表达式为:
yn(m)=xn(m)-2xn1(m)+xn2(m)
(7)
图1 双脉冲对消器示意图
Fig.1 Schematic diagram of double pulse canceller
动目标检测利用多普勒滤波器组来抑制各种杂波。当运动目标和各种杂波的回波信号进入接收端时,在时域是很难区分的,需要根据它们多普勒频率的不同在频率进行区分。杂波和目标多普勒频率不同,设置一个窄带多普勒滤波器组,使其覆盖整个重复频率的范围,杂波和目标回波将出现在不同滤波器的输出端,从而达到从强杂波中检测目标的目的。
窄带滤波器可以用FFT来实现。重复周期数设为NCPI=2n+2,经过双脉冲MTI对消器后输出为Np=2n个周期,方便用FFT实现MTD。对同一距离单元、不同脉冲的输出信号yo(t)进行Np点DFT处理后:
(8)
分析上式知,当fdTr-k/Np=0时,输出有峰值。如果输出通道k有目标,则据此求得目标速度为:
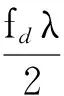
(9)
1.3 基于相位编码的MIMO引信系统
设引信采用收发共用天线,发射阵元Mt=4,接收阵元数Nr=4,一个脉冲周期内码字数目N=40,脉冲占空比p=2/5,脉冲数n=16,码频fm=105Hz,载频fc=2×105Hz,采样频率fs=108Hz。
4路发射端的相位编码采用QPSK调制,接收端采用正交解调方式,经过匹配滤波,DBF,MTI,MDT,CFAR等处理流程,图2(a)为MTD三维输出,图2(b)表示距离和幅度的二维MTD输出图,图2(c)表示速度和幅度的二维MTD输出图。
图2中坐标说明:距离门:此处距离门指采样点的序列号。速度门:速度门轴对应着MTD处理中多普勒滤波器组的序列号。幅度:此处幅度为MTD处理后的输出为标量。
图3给出了目标分别距离30 m,40 m,50 m时真实值与估计值的关系,可以看出,此算法可以精确地测量目标距离。
2 有源压制式干扰对MIMO引信干扰机理分析
MIMO引信的发射信号在频谱上的带宽一般不是连续的,甚至各个发射信号所占用的带宽没有重叠的部分(比如OFDM线性调频发射信号)。但是该课题研究的基于相位编码信号的MIMO引信每路信号的载频一样,频域分布基本一致,所以一般干扰机进行干扰时只需要使用单一的干扰带宽去覆盖所有信号即可。
2.1 干扰波形对MIMO引信影响分析
以噪声调频干扰为例,噪声调频干扰是遮盖性自卫干扰所使用的干扰中较为常见的手段,其干扰时域表达式为:
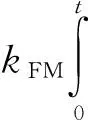
群众路线是我党取得革命胜利和社会经济建设大发展的核心方法,群众工作是我党最具特色的政治工作。从革命党到执政党的政治、历史地位的改变,党的执政根基始终是广大群众。党的智慧源于群众的智慧,党的发展依赖于群众的发展,党的领导植根于群众的支持。新时期,经济快速发展,社会矛盾凸显,党群关系恶化迹象明显,党的核心凝聚力受到严重的影响,社会稳定性也受到极大的冲击,我党必须进一步发展党的群众路线,强化党的核心凝聚力,构建新时期的社会凝聚力。
(10)
式中,调制噪声是零均值广义平稳随机过程;φ为[0,2π]均匀分布,并且是与un(t)相互独立的随机变量;Uj为噪声调频信号的幅度;fj为干扰中心频率,kFM为调频斜率[12]。
通常为了充分利用干扰机的发射功率,会采用瞄准式干扰,即将干扰信号通过一个指定带宽的滤波器之后发射出去,其表达式为:

(11)
假设MIMO引信信号所占频带已经被侦察设备测出,则干扰机发射的干扰信号表达式可由上式(2)表示,干扰频谱示意图如图4。
MIMO引信发射的信号为相位编码信号,数学表达式为:
S=[s1(t),s2(t),s3(t),s4(t)]=[a(t)ejφ1(t)ej2πf0t,
a(t)ejφ2(t)ej2πf0t,a(t)ejφ3(t)ej2πf0t,a(t)ejφ4(t)ej2πf0t]
(12)
式中,a(t)ejφi(t)表示复包络,φi(t)表示第i路的相位调制函数,f0表示载波信号的频率。由于引信使用的是四相编码,所以φ(t)有4个值,为0,π/2,π,3π/2。
假设引信离目标距离为r。目标的响应函数为:
r(t)=σδ(t-τ)ej2πfdt
(13)
其中,τ=2r/c,r是光速,fd是目标的多普勒频率。那么目标的回波可以表示成:
P=[p1(t),p2(t),p3(t),p4(t)]T=r(t)*
[s1(t),s2(t),s3(t),s4(t)]T=r(t)*S
(14)
所以,引信接收到了加入干扰的回波信号进行脉冲压缩,其匹配滤波所输入的信号是:
u(t)=p(t)+G(t)=r(t)*s(t)+J(t)*h(t)
(15)
U(f)=R(f)S(f)+J(f)H(f)
(16)
其中,U(f),R(f),J(f),H(f)分别为u(t),r(t),s(t),h(t)的傅里叶变换。
U(f)经过匹配滤波的输出为:
MF(f)=U(f)S*(f)=R(f)|S(f)|2+
J(f)H(f)S*(f)
(17)
与其对应的时域输出为:
mf(t)=r(t)·F-1[|S(f)|2]+
G(t)·F-1[S(f)]
(18)
其中,F-1[|S(f)|2]叫做点扩展函数(Point spread Function),可以将其看成一个增益。由此可见,相位编码信号和任何一个函数进行卷积,经过匹配滤波(脉冲压缩)后,这个函数的输出结果就是其本身与点扩展函数的卷积。这样,就说明该函数通过脉冲压缩获得了相应的增益。所以这种情况下可以认为这种充分利用噪声带宽相对于一般大带宽噪声调频干扰这种形式的干扰可以以较低的功率达到较好的干扰效果。从频域角度又可以将相位编码信号看作一个频带为[f0-B/2,f0+B/2]的滤波器,而用噪声通过这样一个滤波器。当干扰带宽与信号带宽重叠时,MIMO引信抗干扰能力是最弱的,即此时给干扰加一载频,那么它在频域的带宽分布就与其中心频率有关,干扰能力是最强的。
2.2 有源压制式干扰对MIMO引信信噪比影响分析
假设干扰机功率一定前提下,对比分析3种干扰对MIMO引信的影响。
噪声调幅干扰为:
J(t)=[Uj+un(t)]cos(2πfjt+φ)
(19)
式中,调制噪声un(t)是零均值广义平稳随机过程;φ为[0,2π]均匀分布,并且是与un(t)相互独立的随机变量;Uj为噪声调幅干扰信号的幅度;fj为干扰中心频率[12]。
噪声调幅信号的总功率为:
(20)
假设回波有用信号功率为Pr。则引信匹配滤波之前的输入信噪比为:
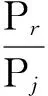
(21)
噪声调频干扰表达式如式(1)所示,其功率等于载波功率:
(22)
因此,调制噪声功率不对已调的功率发生影响。
假设回波有用信号功率为Pr。则引信匹配滤波之前的输入信噪比为:
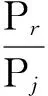
(23)
噪声调相干扰表达式为:
J(t)=Ujcos[2πfjt+kpmun(t)+φ]
(24)
式中,调制噪声un(t)是零均值广义平稳随机过程;φ为[0,2π]均匀分布,并且是与un(t)相互独立的随机变量;Uj为噪声调幅干扰信号的幅度;fj为干扰中心频率,kpm为常数[12]。
经计算,调相噪声的总功率为载波功率:
(25)
假设回波有用信号功率为Pr。则引信匹配滤波之前的输入信噪比为:
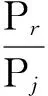
(26)
对比上面三种干扰,噪声调幅干扰在三者之中使得输入信噪比最小,经过匹配滤波后的输出信噪比最小。换言之,噪声调幅干扰在这三者中对MIMO引信影响是最大的,而调相和调频干扰对MIMO引信的影响基本是相同的。
3 仿真研究
3.1 干扰频率在载频处压制式干扰对引信影响分析
1)在发射过程中加入噪声调相干扰,当有效相移足够大时,适合作为遮盖性干扰信号,设置kpm=103,压制噪声的中心频率fj=fc=2×105Hz,调制噪声un(t)设为高斯白噪声,初始相位φ均设为0,在实验过程中为了符合实际,将理想高斯白噪声通过一个低通滤波器限制其带宽,由小到大地改变噪声调相干扰的幅度值Uj,当Uj=11.8,MTD输出如图5所示,不能正确得到距离和速度信息。计算出信噪比SNR=-4.352 dB,即当信噪比SNR<-4.352 dB时,此MIMO系统无法正确检测目标。
2)在发射过程中加入噪声调幅干扰,调制度m=0.5,调制噪声un(t)设为高斯白噪声,初始相位φ均设为0,当Uj=12,MTD输出如图6所示,MTD主峰几乎被干扰峰淹没,即SNR<-4.411 dB时,此MIMO系统已无法正确检测目标。
3)在发射过程中加入噪声调频干扰,调频斜率kfm=15,调制噪声un(t)设为高斯白噪声,初始相位φ均设为0,当Uj=11.3,MTD输出如图7所示,主峰已经淹没在干扰之中,即SNR<-4.117 dB时,此系统已无法正确检测目标。
采用Monte Carlo实验来衡量三种有源干扰对检测性能的影响。定义求根均方误差(Root Mean Square Error,RMSE)为:
(18)
由经过Monte Carlo实验后的RMSE结果可知,基于相位编码的MIMO引信系统对高斯白噪声的抗干扰性能明显高于其他三种干扰,噪声调幅干扰、噪声调频干扰、噪声调相干扰对回波信号作用时,把干扰频率对准载频,在干扰功率一样的前提下,噪声调幅干扰对MIMO引信检测性能影响最大。
3.2 干扰频率偏离载频压制式干扰对引信影响分析
从小到大地改变干扰信号频率与发射信号频率的差值,观察各种情况下,干扰对系统检测性能的影响。以噪声调幅干扰为例。
1)当加入噪声调幅干扰时,设置干扰频率fj=0.6fc,Uj=12,仿真结果如图9所示。
对比图6,发现当干扰信号到达接收端与引信发射信号频率相差较远时,干扰旁瓣明显降低,能从主峰位置提取出相关参数,此时干扰信号对MIMO引信系统影响较小。
2)当干扰信号到达接收机的频率与发射信号频率差,接近于多普勒频率时,设置fj-fc=fd,Uj=12,仿真图像如图10所示。
对比图6,当干扰信号到达接收端的频率与引信发射信号频率相差接近于多普勒频率时,干扰旁瓣比干扰频率在载频处时提高了,对MIMO引信系统的影响最大,此时的干扰信号类似于目标回波信号,干扰带宽完全覆盖回波信号,对MIMO引信测距测速影响最大。
4 结论
本文分析了有源压制式干扰对MIMO引信测距测速的影响。从干扰波形方面分析干扰机理,并从信噪比增益方面对比分析了三种常见有源干扰对基于相位编码MIMO引信测距测速的影响。理论分析及仿真结果均表明,功率一定前提下,干扰带宽与回波信号带宽重叠即干扰中心频率与回波信号一致时,对相位编码体制MIMO引信测速测距影响最大。噪声调频、噪声调相、噪声调幅这三种常见有源压制式干扰在干扰中心频率在载频处且干扰功率一致的前提下,噪声调幅干扰使输出信噪比最低,对测距测速影响最大。有源压制式干扰在低信噪比情况下,仍然能够有效地干扰相位编码体制的MIMO引信,今后可通过展宽干扰频谱或者通过增加输出信噪比等途径考虑抗干扰算法,在今后的研究过程中会跟进提出相关抗干扰算法。
[1]唐斌,赵源,蔡天一,等.雷达抗有源干扰技术现状与展望[J]. 数据采集与处理,2016, 31(4):623-639.
[2]赵晓燕. 噪声干扰对相位编码雷达干扰效果分析[J]. 中国科技信息,2014, 23(8): 42.
[3]Jiang Jiawei, Wu Yanhong, Wang Hongyan. Analysis of active noise jamming against synthetic aperture radar ground moving target indication[C]// China: CISP, 2015:1530-1535.
[4]Zhang Juan, Liu Nan, Zhang Linrang. Active jamming suppression based on transmitting array designation for colocated multiple-input multiple-output radar[J]. IET Radar, Sonar &Navigation, 2016,10(3):500-505.
[5]陈金立. 相位编码MIMO雷达信号处理技术研究[D]. 南京:南京理工大学,2010.
[6]Wang Xiaojing, Xiong Ying, Li Yuhao, et al. Modulation recognition of MIMO radar signal based on joint HOS and SNR algorithm[J].Journal of Systems Engineering and Electronics,2014, 5(2):226-236.
[7]Xu Hangrong, Liu Song, Liu Jingping, et al. Composite waveform set of phase coding and linear fm for MIMO Radar[J]. Applied Mechanics and Materials, 2013, 421:731-736.
[8]刘晓莉. MIMO雷达参数估计方法研究[D]. 西安:西安电子科技大学,2011.
[9]巩朋成. MIMO雷达波形优化与参数估计方法研究[D].成都:电子科技大学,2014.
[10]庞娜. MIMO雷达信号处理技术及实现研究[D]. 北京:北京理工大学,2015
[11]Li Jian, Peter Stoica. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007(5): 106-114.
[12]赵惠昌,张淑宁. 电子对抗理论与方法[M]. 北京:国防工业出版社,2010.
