OQAM/OFDM系统改进的预编码信道估计
2018-01-12,,,
,,,
(空军工程大学防空反导学院,陕西 西安 710051)
0 引言
偏移正交幅度调制的正交频分复用技术[1-3](Offset Quadrature Amplitude Modulation/Orthogonal Frequency Division Multiplexing,OQAM/OFDM)是近年来提出的一种基于滤波器组的多载波调制技术。与正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)系统相比,OQAM/OFDM系统采用了具有良好时频聚焦特性的原型滤波器,能够有效地降低带外辐射,提高系统的功率利用率;且OQAM/OFDM系统不需要采用循环前缀(Cyclic Prefix,CP)或者其他保护间隔,提升了系统的频谱利用率。相比于OFDM系统的优势,使OQAM/OFDM系统已经成为新一代无线通信系统和电力线通信(Power Line Communication,PLC)的备选方案之一,具有很强的发展潜力。
但是由于原型滤波器的使用,使OQAM/OFDM系统仅满足在实数域正交,使系统在传输过程中受到虚部干扰,传统的OFDM系统的信道估计技术不再适用于OQAM/OFDM系统,需要研究新的信道估计方法,目前OQAM/OFDM系统信道估计方法主要有基于导频序列的信道估计方法[4-6]和基于离散导频的信道估计方法[7-14]。
基于离散导频的信道估计方法常用的有辅助导频法[7]和预编码法[14](Auxiliary Pilot,AP)。AP法是通过在导频周围的任意时频格点放置辅助导频消除系统存在的虚部固有干扰,该方法在每个信道估计导频处使用两个实数符号,与OFDM系统在每个导频处使用一个复数符号占用的频谱资源相同,但是辅助导频处功率高。为了降低导频功率,文献[8]提出了在导频周围插入两个辅助导频的方法(Composite Pilot Pairs,CPP),该方法有效地降低了辅助导频处的功率,但是在一个导频处使用三个实数符号会降低频谱利用率。C.Lélé等在文献[14]中提出了一种在发送端导频周围采用预编码的方法对导频周围的干扰进行消除,该方法不需要额外的导频功率,但是在发送端需要计算编码矩阵C,计算的复杂度较高。本文针对上述问题,提出了OQAM/OFDM系统改进的预编码信道估计算法。
1 OQAM/OFDM系统模型
OQAM/OFDM系统发送端发送的信号为:
(1)

发送信号经过无线信道之后,接收端的信号表示为:
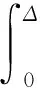
(2)
式中,Δ是多径信道的最大传播时延,h(t,τ)为多径信道的脉冲响应,n(t)表示均值为零,方差为σ2的高斯白噪声。将式(1)代入式(2)中:
(3)
g(t-τ-nτ0)选用具有良好时频聚焦特性的滤波器,当τ∈[0,Δ]时,可以近似认为g(t-τ-nτ0)≈g(t-nτ0),则式(3)可以表示为:
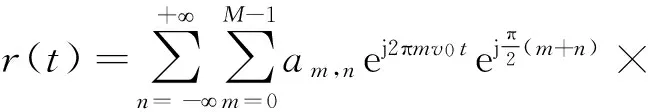
(4)
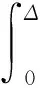
经过解调后的输出信号为:

(5)
式中,n′(t)=〈n(t),gm0,n0〉仍为服从高斯分布的白噪声信号。〈gm,n,gm0,n0〉R表示对gm,n和gm0,n0进行内积并取实部。
在OQAM/OFDM系统中,发送端和接收端滤波器满足在实数域正交,即:
〈gm,n,gm0,n0〉R=δm,m0δn,n0
(6)
δm,m0与δn,n0表示两个狄拉克函数。
由于发送端和接收端之间只存在实数域正交,接收到的经过复数信道的信号会引入虚部干扰。当采用具有良好时频聚焦特性的滤波器时,虚部干扰主要来自导频符号的一阶邻域,则式(6)可以表示为:
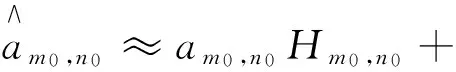
(7)
在慢衰落信道中,信道的频率响应在一阶邻域内基本不变,则上式可以表示为:
(8)
2 改进的预编码信道估计方法
2.1 离散导频预编码信道估计
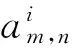
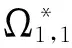
(9)
假设a=(a1,…,a8)T为对导频周围数据预编码后发送符号;d=(d1,…,d8)T为发送端实际数据符号;C=[c1,…,c8]为预编码矩阵,可以得到:
a=Cd
(10)
如果矩阵C为非奇异矩阵,则在接收端可以通过计算d=C-1a得到数据向量d。同时,如果C为正交矩阵,即CTC=I,那么可以得到:
‖a‖=aTa=dTCTCd=‖d‖
(11)
从式(11)可以看出,编码前后数据符号的功率相同,即采用预编码方法不会增加额外的功率消耗。设γk=〈gm,n,gm0,n0〉R表示相应位置的干扰系数,令γ=(γ1,…,γ8)T,则

(12)

(13)
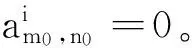
2.2 改进预编码方法
在上一节中假设d8=0,由式(9)可以得到:
a=Cd=Dd′
(14)
式中,d′=(d1,…,d7)T,D=(c1,…,c7)表示编码矩阵,则式(12)可以表示为:
(15)
γTD=0
(16)
上节中为保持编码前后符号功率不变,C为正交矩阵。因此,D应同样满足DTD=I。
由上面的分析可以得到,问题转化为求编码矩阵D。若对导频一阶邻域内的所有符号进行编码,则D为8×7矩阵,由上一节中求C的施密特正交化的方法可以求得,但是计算复杂度仍然比较大。为有效地减少算法的计算量,考虑降低D的维数。
由图1所示的导频周围数据结构示意图,只对格点位置k=1,2,3,4处的符号进行编码,使四位对导频符号的干扰和为零。此时,a=(a1,…,a4)T,d′=(d1,…,d3)T,γ=(γ1,…,γ4)T,D=(c1,…,c3)为4×3的编码矩阵。
对于使用IOTA原型滤波器的OQAM/OFDM系统,可以得到:γ=(-0.4411,0.4411,0.4411,-0.4411)T。选取编码矩阵D的前两列为:

第三列c3与γ,c1和c2正交的单位向量,可以得到
(17)
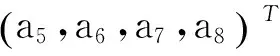
θ′=γ′Ts
(18)
为消除格点k=5,6,7,8处存在的干扰,对式(14)进行如下变换:
a=Dd′+χ
(19)
由上式可以得到,若选择合适的χ,使上式满足γTa=-θ′,则剩余格点处的干扰θ′将被抵消。由γTD=0可得γTχ=-θ′。为减少导频功率的消耗,通过最优化问题求解χ:
min|χ|2,满足γTχ=-θ′
(20)
通过拉格朗日乘子法可以求得:
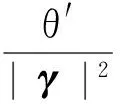
(21)
通过将式(14)变换为式(19),降低了计算矩阵的复杂度,同时消除一阶邻域内所有符号对导频的干扰。
3 性能分析
本节主要从频谱效率、能量效率、计算复杂度三个方面对上节两种方法和AP法三种方法进行分析。
3.1 频谱效率分析
在AP法中,除导频符号本身以外,仍需要一个辅助的实值符号用以消除干扰。对于预编码方法和本文提出的改进预编码方法同样需要一个额外的实值符号作为导频开销,并将其置为零。因此,三种方法的频谱效率相同。
3.2 能量效率分析


(22)
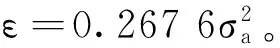
由上面的分析可以得到,本文比预编码法增加了额外的功率消耗,但是相比于AP法的功率消耗有很大的降低,在可以接受的范围之内。
3.3 计算复杂度分析
在实际的硬件实现过程中,乘法运算远比加法运算实现复杂。因此在本文中,只考虑三种方法的乘法运算复杂度,不考虑加法运算的复杂度。
在AP法中,辅助导频值的确定需要额外计算导频周围的数据。其计算公式如下:
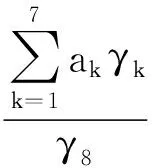
(23)
由公式可以看出,AP法需要7次乘法运算和一次除法运算(本质也是乘法运算),共需要8次实数乘法运算。计算复杂度为O(N0)。
在本文提出的改进预编码算法中,在发送端和接收端共需要矩阵运算4×4×2=32次,对于每一个OQAM/OFDM系统,由于滤波器函数已知,则干扰系数γ已知,则求χ共需要4+4+1=9次乘法运算,本文所提方法共需要41次乘法运算,计算复杂度为O(N1)。
在预编码算法中,在发送端和接收端共需要乘法运算8×8×2=128次,计算复杂度为O(N2)。
从以上分析中可以得到,本文所提方法在计算复杂度上比预编码法减少一个数量级,但比AP法增加一个数量级,但其整体复杂度能够满足实际应用的需求。
综上所述,本文所提的改进方法是辅助导频法和预编码方法的一个折中方案,以较小的导频功率消耗带来算法的计算复杂度的降低。
4 仿真分析

图2和图3分别表示本文所提的改进预编码法和文献[14]中提的预编码法对比以及改进预编码法与其他离散导频信道估计方法误比特率(Bit Error Rate,BER)比较。从图2可以看出,改进的预编码方法与编码数为8的预编码法BER性能相近,比编码数为3的预编码法性能有很大的提升。图3中为不同离散导频信道估计方法误比特率性能的比较分析,改进预编码法比AP法性能上有所提高,当信噪比(Signal-Noise Ratio,SNR)大于5 dB时,改进预编码法比成对导频序列(Pair of Pilot,POP)离散导频方法性能提高1 dB,SNR大于7时提高了2 dB。
归一化均方误差(Normalized Mean Square Error,NMSE)是反应信道估计准确度的一个重要指标,其计算公式可以表示为:
(23)
图4和图5展示了本文所提方法与其他离散导频信道估计方法NMSE仿真结果。图4仿真本文所提出的改进预编码法和不同数据编码数的预编码方法对比。从结果中同样可以看出,改进的预编码法与编码数为8的预编码法有相近NMSE性能;与编码数为4的预编码法有很大的性能提升,当SNR大于6 dB时,改进预编码法比其性能提升2 dB左右,当SNR大于8时,性能提升能够达到3 dB。
图5表示不同离散导频情况下NMSE性能对比,从图中可以看出,改进的预编码方法的NMSE性能比AP法性能有一定的提升,与预编码法的性能相近;当SNR大于6 dB时,改进的预编码方法比POP法性能提升3 dB,当SNR大于8 dB时,性能提升4 dB。
图6仿真AP法,预编码法和本文提出的改进预编码法复杂度分析。图中横轴表示导频在频域上的间隔,纵轴表示在一个时间点上三种不同的方法所需要进行的乘法次数。从图中可以看出,改进的预编码法的复杂度在AP法和预编码法之间,相比于预编码法,改进的预编码法复杂度降低了一半。
从仿真的结果中可以看出,本文提出的改进预编码方法与编码数为8的预编码法相比,在信道估计性能上相同,但是改进预编码法复杂度相比于传统的预编码法降低了一半,虽然增加额外的功率消耗,但功率消耗的增加在可接受的范围之内。在实际应用中,受功率设备和硬件速率的影响,信道估计的额外功率消耗和计算复杂度都不能过高,因此本文所提方法更适合于实际应用。
5 结论
本文研究改进的预编码离散导频信道估计算法,通过减少预编码法的编码数改进传统预编码法复杂度过高的问题,同时相比于AP法,本文所提的算法额外的功率消耗在可以接受的范围内。仿真结果表明,本文所提的算法在信道估计性能上与AP法和预编码法相近,但是在复杂度和额外的功率消耗上是两种算法的折中,因此相比于两种算法更具有实用价值。
[1]Farhang-Boroujeny B. OFDM Versus Filter Bank Multicarrier[J]. IEEE Signal Processing Magazine, 2011,28(3):92-112.
[2]Hanen B. Theoretical analysis of BER performance of nonlinearly amplified FBMC/OQAM and OFDM signals[J]. Journal on Advances in Signal Processing, 2014,2014(1):1-16.
[3]Saeedi-Sourck H. Complexity and Performance Comparison of Filter Bank Multicarrier and OFDM in Uplink of Multicarrier Multiple Access Networks[J]. IEEE Transactions on Signal Processing, 2011,59(4):1907-1921.
[4]Liu W. Preamble Overhead Reduction with IAM-C for Channel Estimation in OQAM-OFDM Systems[C]// IEEE China Summit and International Conference. US: IEEE,2015:1-5.
[5]ZHAO Y. Iterative Preamble-Based Time Domain Channel Estimation for OFDM/OQAM Systems[J]. The Institute of Electronics, Information and Communication Engineers, 2016,E99B(10):2221-2227.
[6]Savaux V, Louet Y, Bader F. Low-Complexity Approximations for LMMSE Channel Estimation in OFDM-OQAM[C]// International Conference on Telecommunications. Greece,2016:1-5.
[7]Javaudin J, Lacroix D, Rouxel A. Pilot-aided channel estimation for OFDM_OQAM[C]// IEEE Semiannual Vehicular Technology Conference. Orlando: IEEE,2003:1581-1585.
[8]Zhao Z, Vucic N, Schellmann M. A simplified scattered pilot for FBMC_OQAM in highly frequency selective channels[C]// International Symposium on Wireless Communications Systems. 2014:819-823.
[9]Choi J. Interference-dependent pair of pilots for channel estimation in FBMC systems[C]// IEEE International Symposium on Broadband Multimedia Systems & Broadcasting. US:IEEE, 2016:1-4.
[10]Nissel R, Rupp M. On pilot-symbol aided channel estimation in FBMC-OQAM[C]// IEEE International Conference on Acoustics. US:IEEE,2016:3681-3685.
[11]Mestre X, Kofidis E. Pilot-based channel estimation for FBMC-OQAM systems under strong frequency selectivity[C]// IEEE International Conference on Acoustics. US: IEEE,2016:3696-3700.
[12]Fuhrwerk M, Moghaddamnia S, Peissig J. Scattered Pilot based Channel Estimation for Channel Adaptive FBMC-OQAM Systems[C]// IEEE Transactions on Wireless Communications.US: IEEE, 2016:1-17.
[13]Cui W. Coded auxiliary pilots for channel estimation in FBMC-OQAM systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(5):2936-2946.
[14]Lélé C. Iterative scattered-based channel estimation method for OFDM/OQAM[J]. EURASIP Journal on Advances in Signal Processing, 2012,2012(1):1-14.
