基于积分渐进展开的气相色谱重叠峰快速解析法

2018-01-11高清维卢一相

色谱 2018年1期

柯庆, 高清维, 卢一相

(安徽大学电气工程与自动化学院, 安徽合肥 230601)

气相色谱学是20世纪后期分析化学领域的重大突破,它将分析化学与信号检测完美地结合在一起,定量测定物质的组分。色谱定量分析的手段是计算单个色谱峰面积或色谱峰高度,简称峰面积法或峰高法[1],因此色谱峰面积和峰高计算是色谱定量分析的核心技术。但是化学组分相近物质的色谱峰是重叠的[2],无法直接计算纯组分单峰面积和峰高,所以准确地将重叠峰解析就成为色谱研究的重点之一。

经典的重叠峰解析有垂线法、切线法、均线法和三角法等几何解析方法[2,3],这些方法的优点是直观易操作,便于色谱的实时处理;缺点是对峰底分离度(R)要求高,误差大。近年来,随着计算技术的发展,数值计算被广泛用于重叠峰解析[1,4,5],例如函数拟合法和最小平方曲线拟合法,这些方法对峰底分离度要求低,但是计算中需反复调整拟合参数,导致计算量大,耗时长,难以用于色谱的实时处理。另一类方法是非数值解析法,如神经网络解析方法[6]和傅里叶变换方法[7]。神经网络解析方法有较强的预测和容错能力,解析准确度高,缺点是收敛速度慢,不稳定,网络的初始值、学习率和网络结构都难以确定;傅里叶变换方法计算简便,但需要事先确定重叠峰中单峰的峰高、峰形和半峰宽,这在实际分析中难以实现。近年来小波变换被用于重叠峰解析[8,9],这个方法只做简单求和,故而运算速度快,但小波基选取困难、小波解析层数难以确定。这些结果表明非数值方法仍需进一步发展,数值方法仍是重叠峰解析的主流方法[10-12]。同时数值解析的方法本身也不断推陈出新,例如近年来出现的多元曲线分辨方法[13],这些新理论和新方法推动了色谱学的快速发展[14]。

很明显,单峰表达式对重叠峰的解析至关重要。理想情况下,色谱峰应当是高斯正态分布。但是,由于各种物理与化学原因,实际色谱峰偏离高斯分布,形成不对称的拖尾峰和前伸峰。多种色谱单峰函数用来表达不对称色谱峰,其中典型的是GPA(Gaussian peak adjustment)函数[15-17]或称AGD(asymmetric Gaussian distribution)函数[4]以及EMG(exponentially modified Gaussian)函数[12]。GPA函数用两个标准差不同的半高斯峰组合成不对称峰,具有参量少、计算快的优点;但是表示高度不对称的色谱峰误差较大[12,16,17]。EMG函数用卷积修正高斯对称函数,对曲线逐点匹配,形成非对称分布函数,其结果适用范围广,缺点是表达式复杂、不能准确表达对称性较好的色谱峰。同时,EMG函数解析得到的形状与初值选取有关,计算的鲁棒性差,效率低[4,12]。有多种修正的EMG函数,如GEMG (generalised exponentially modified Gaussian)函数和PMG1(polynomial modified Gaussian function 1)函数,但这些函数都比EMG函数更复杂,计算效率更低[12,15]。由于这些原因,GPA函数仍然被广泛地应用于LSV和CV(linear sweep and cyclic voltametry)系统以及色谱快速解析中[16,17]。这篇论文考虑气相色谱峰和一般色谱峰的在线处理,气相色谱单峰可用GPA函数表示,为了实时解析重叠峰,非气相色谱峰也选择了较为简单的GPA函数来近似表示它的单峰。

考虑到面积是一个积分过程,积分方程解积分问题的相对误差小,积累误差也小,能得到理想的结果,论文中用积分方程和积分渐进级数解析气相色谱重叠峰。论文将前伸或拖尾峰用GPA函数表示,列出重叠峰中GPA函数的积分方程和约束条件,再用积分渐进级数展开积分方程,进而得到计算单峰面积和峰高的代数方程。该法精度高,速度快,无需人工干预,既适合在线实时处理也适合色谱工作站。

1 重叠峰解析模型

1.1 单峰面积计算

图1是单组分非对称色谱示意图。从图1可知流出曲线的GPA函数表达式为[17]

(1)

式(1)中C(x)为色谱检测器的检测信号值,它可以是电压、电流等参量,通常称为信号强度[1];H0为峰高;xG对应于信号强度极大值点的位置(即保留时间);σ1和σ2为色谱峰的标准偏差。

图 1 非对称高斯色谱峰示意图Fig. 1 Schematic diagram of the asymmetric Gaussian chromatographic peak

不对称因子AS表示峰形状的不对称程度。如图1所示,定义峰高10%处,色谱峰上两点到中心垂线的距离分别是DL和DR,可得到[18]

(2)

AS>1称作前伸峰,AS<1称作拖尾峰。

由式(2)可导出GPA函数AS的计算公式是

(3)

σ1和σ2分别是图1中信号强度C(x)的左侧半峰和右侧半峰的标准偏差。

GPA峰的面积是

(4)

1.2 重叠峰的解析模型

纯组分样品在色谱图中对应的是单峰,色谱峰峰高和峰面积可分别用式(1)和式(4)计算。但是不同的纯组分样品在色谱图中重叠后,形成3种模式的重叠峰:谷峰模式、肩峰模式和完全重叠峰模式。这些模式里的纯组分色谱峰(以下简称单峰)在实验中不能提前获得。文献[1]和文献[15]提出气相色谱重叠峰的单峰相似原理:组分如果有非常类似的结构和性质,它们在色谱分离中将趋向类似分布,这将导致组分分离失败,形成重叠峰,因此同一重叠峰的纯组分色谱峰形状相似;重叠峰中的各纯组分色谱信号强度的单峰函数之间存在一个比例因子,某纯组分信号强度单峰函数乘以一个比例因子,再平移,它将与另一纯组分信号强度色谱单峰函数相同。虽然这两个函数之间可能有一些差异,但是这个差异很小。文献用相似原理解析了间二甲苯(m- xylene)和对二甲苯(p- xylene)混合溶液[1]、油酸盐(oleate)[2]等物质[15,18]的色谱重叠峰,结果与实验结果符合较好。

首先讨论两个纯组分物质组成的重叠峰解析模型。设单峰A和B如图2a所示,它们重叠成如图2b所示的谷峰。根据相似性原理,如果A峰和B峰的信号强度函数分别是CA(x)和CB(x),则有

CA(x)≡ηCB(x+x0)

(5)

图 2 重叠峰参数示意图Fig. 2 Schematic diagrams of overlapping peak parameters a. parameters of similar peak A and peak B; b. the overlapping valley peak.

式中η是比例因子,x0是平移坐标。将式(1)代入式(5),得到重叠峰中的两个纯组分色谱单峰的GPA函数[15]分别是

(6)

(7)

式中xA和xB分别是纯组分A峰和B峰的峰高的横坐标,HA和HB分别是它们的峰高;σ1和σ2分别是纯组分GPA函数的半峰标准偏差。式(6)和式(7)中只要令σ1=σ2,就是高斯峰。

从式(6)和式(7)可知,确定重叠峰中的单峰,除需σ1、σ2和峰高外,还要知道色谱峰的保留时间(峰高的位置)。3种重叠峰峰高位置的解法如下[2,11]: 1.重叠峰是谷峰,色谱图上重叠峰的2个极大值点的位置(重叠峰峰高位置)就是纯组分单峰的峰高位置xA和xB; 2.重叠峰是没有谷点的肩峰,色谱图上只能确定一个极大值点,这一点就是大峰的峰高位置。而小峰的峰高位置可以从色谱图的重叠峰拐点切线求出,详细算法见1.4节“肩峰的解析”;3.重叠峰是完全重叠峰,无法直接从色谱图上确定两个单峰的峰高位置,完全重叠峰一般用曲线拟合法解析,本文不考虑完全重叠峰解析。

1.3 谷峰解析算法

(8)

从1.2节可知谷峰的两个极大值点就是两个单峰的顶点,因此SⅠ由A峰的半单峰面积SAⅠ和B峰重叠在曲边形CA′A″的面积组成,于是有

(9)

式(9)中,令t=(x-xB)/σ1,可得

(10)

式(10)中的Φ(z)为正态分布的累积函数。由于SAⅠ和SBⅠ分别是GPA函数的半峰面积,对式(6)与式(7)积分,积分下限都取-∞,上限分别取两个GPA函数最大值点坐标xA和xB,得到

上两式带入式(10),可得

故有

(11)

其中的σ1为A峰左半峰的标准偏差。

从图2b和1.2节又知,HA′是A峰的峰高与B峰在点A″处的高度值之和;HB′是B峰的峰高与A峰在B″处的高度值之和。从图2b可求出A、B两峰峰高的约束方程分别是

(12)

(13)

综合上述结果可以得到两纯组分重叠谷峰解析的方程组为

(14)

1.4 肩峰的解析

肩峰只有一个极大值点,只能找到一个单峰的顶点,谷峰解析的方法不能直接应用。文献[2,19]介绍了如何用两纯组分肩峰拐点求单峰顶点,图3是该方法的示意图。图中峰A顶点A′的位置是A″。曲线A′C′之间有单峰B的顶点,过曲线A′C′之间的拐点P1(x1,y1)和P2(x2,y2)分别做两条切线,切线交点P0(x0,y0)的横坐标x0是未知单峰B的顶点的横坐标,这个新顶点位置是曲线A′C′之间的P0′点,见图3。连接点C、A′、P1、P0′、P2和C′组成新的谷峰。用A′和P0′作为两个峰的顶点,再用1.2节中的重叠谷峰方法列方程,其方程组与1.2节中所列的方程组相同,这里不再重复。

图 3 肩峰解析示意图Fig. 3 Schematic diagram of resolving a shoulder peak

2 峰分离方程的数值算法

2.1 重叠峰区域面积的计算

式(14)中的S和SⅠ分别是整个重叠峰的面积和区域Ⅰ的面积。S和SⅠ的值可以用数值积分从所给的重叠峰数据求出,这里用复化辛普森公式求面积的值。复化辛普森公式[20]是

(15)

其中L为积分的起点;R为积分的终点;h为步长。由式(1)可知,SⅠ积分的起点应在-∞处,故L=-∞。实际的积分无法找到-∞点,但对应于-∞点有

由图2b可知,SⅠ积分起点应当取f(x)=0的C点。同理可知,S积分的起点是点C,终点是点C′,这样就求出了SⅠ和S。

2.2 积分方程的简化与展开

解式(14),并利用误差函数

得到

因谷峰和肩峰的峰高位置xA和xB相距较远,exp[-(xA-xB)2/2σ2]<1是一阶小量,故o(xA,xB)是二阶小量,有o(xA,xB)≪1,将其略去。上式可写成

(16)

取erf(z)的渐进级数前4项[20],则有

(17)

将式(17)代入式(16),略去2阶小量o(xA,xB),得到

(18)

从式(14)可导出

从前面讨论可知,o(xA,xB)≪1,故略去,得

(19)

综合式(18)、式(19)和式(14)的第一式和最后一式,可得到方程组

(20)

式(20)中的σ1、σ2、HA和HB是待求解的未知数。

式(20)是非线性超越方程组,没有解析解,可用迭代法求解,这里用Gauss- Seidel迭代法求解,迭代格式是

(21)

其中k是迭代的次数。若式(21)收敛,则有

很明显式(21)的解就是式(20)的解。

多个单峰组成的重叠峰解析问题,其解析方法与两个单峰组成的重叠峰解析模型类似,都是列积分方程和约束方程,但是情况更复杂一些。比如多个纯组分的重叠谷峰解析:首先列出积分方程组,用积分渐进公式展开这个积分方程组为代数方程组,以便建立迭代方程求解;其次约束方程中,无法确定单峰峰高位置,因此要增加峰高位置作为未知变量,需要增加新的约束条件,重叠峰极大值点的一阶导数为零的条件是新的约束条件,因此约束方程组更复杂一些。这里不展开讨论这个问题。

2.3 峰高和峰面积的计算方法

可用峰底分离度[2]

(22)

评价重叠峰中纯组分单峰重叠情况。式(22)中xR1和xR2分别是两个单峰的峰高位置,其意义与图1的xG相同。Wt1和Wt2分别是两个单峰的平均宽度。在R从大到小变化时,重叠模式依次经历谷峰模式、肩峰模式和完全重叠峰模式。

两个纯组分单峰组成的重叠峰是谷峰模式,可以找到两个极大值点作为单峰的峰高位置。肩峰模式时,小峰所在的极大值点消失,但两峰曲线相加,小峰的顶点在峰的最大值一侧会形成一个拐点,大峰本身也有一个拐点,于是在峰高的一侧会有两个拐点。为了描述方便,称小峰峰高与大峰曲线叠加而成的拐点为小峰定位拐点,如图3所示,这两个拐点可以定位小峰顶点[2]。实际上,拐点描述了曲线的凹凸点,两峰若重叠的严重,曲线将变得平滑,不再有凹点和凸点,拐点也将消失。从图3可以看到,若定位拐点消失,仅有一个拐点,则无法确定小峰的峰高位置,实际上这时叠峰进入完全重叠模式,方程(20)成立的条件不再具备,文章提出的计算方法失效。因此在计算中,肩峰模式中是能找到两个拐点的,如果只能找到一个拐点则肩峰模式结束,就应结束计算。后继计算表明,在肩峰模式将要消失前,解析结果的误差常常很大。为此可以设定临界值∣f0″ ∣,在定位拐点值(二阶导数值)小于∣f0″ ∣后,就认为肩峰模式消失,结束计算。

完全重叠峰模式时,两峰重叠很严重,谱图上只有一个峰,峰两侧曲线光滑,仅有大峰自身的拐点,小峰峰高位置无法定位,本文所给出的算法失效。

综上所述,两个纯组分色谱重叠峰面积的计算过程如下:对于给定重叠峰的色谱图,首先判断是肩峰还是谷峰。若是肩峰应当根据1.4节的图3,先找出它的两峰峰高坐标和重叠峰的两个峰高,然后用方程组(21)求解两个单峰的峰高和标准偏差;否则直接解谷峰方程组(21)。有了两个单峰参数,可用式(4)求出它们面积。

3 结果与讨论

3.1 气相色谱峰的分离评价指标和仿真数据

峰底分离度R和峰高比(HR)两个参数可用于表示叠峰的分离程度。根据GPA函数定义式(1)和式(22),可导出峰底分离度是[2]

(23)

通常认为R=1.5时,两峰完全分离。

峰高比的定义式为[2]

HR=HA/HB

(24)

式中HA和HB分别表示A峰和B峰的峰高。

误差有面积误差和峰高误差两种。面积误差是

(25)

其中Strue是实际单峰的面积;Smodel是解析峰面积。

峰高计算误差为

(26)

式中Htrue是实际单峰的峰高,Hmodel是解析峰的峰高。

本文在不同的峰高比下,对不同峰底分离度的前伸和拖尾重叠双峰做了仿真验证,仿真程序用VS2010实现。实现过程如下:输入两个GPA函数在不同保留时间差下的重叠峰曲线参数,然后对混合曲线离散化,形成一组离散数据,或直接输入重叠峰的离散数据;再按照2.3节的计算过程,对这一组数据用式(14)、式(20)和式(4)计算解析后的两个峰的峰高和两个单峰面积,其值与真实峰高和峰面积相比较,可以得到它们的误差。

仿真解析了两组分样品重叠色谱峰。设有纯组分样品A、B(B根据峰高大小分为B1、B2和B3 3种情况),它们的峰高分别是HA=100.000 0、HB1=80.000 0、HB2=12.500 0和HB3=6.250 0,则峰高比分别为HR=HA/HB1=1.25,HR=HA/HB2=8.0,HR=HA/HB3=16。

样品A与样品B在不同的标准偏差σ1和σ2下,取AS=σ1/σ2或AS=σ2/σ1,可得到前伸单峰或拖尾单峰,表1是这些色谱峰的参数和面积。峰A与其他3个B峰可形成前伸或拖尾重叠峰。一般情况下,方程(20)迭代7～8次可求出其解,个别重叠峰解析的迭代次数达到20次。

表 1 两组分样品重叠峰里单峰的参数和面积真实值

3.2 前伸峰的仿真结果比较和分析

对表1列举的A峰和峰B1、B2、B3在不同的峰底分离度下解析了它们的前伸重叠峰的峰高和面积。峰高比HR=8.0和不对称因子AS=2.000 0的前伸重叠峰解析后得到的峰高和峰面积与峰底分离度的关系如表2所示,肩峰起始位置在峰底分离度R=0.600 0处。表2的SA和SB2分别是A峰和B2峰面积,其他参数前面已经定义。从表2中的误差可以看到:误差随峰底分离度减小而增大,即误差从谷峰到肩峰逐渐增大,最大误差位于肩峰模式结束处,峰高最大误差2.288 1% ,面积最大误差2.364 9% ;其次,小峰误差并不一定总大于大峰误差,但是峰高和面积的最大误差都是小峰误差。

图4是峰高比HR=HA/HB3=16和HR=HA/HB1=1.25的前伸重叠峰计算误差曲线图。图4 HR=16的b图中AS=1.428 6的A峰曲线与AS=2.500 0的B3峰曲线重合,图4 HR=1.25的b图中AS=1.428 6的B1峰曲线与AS=2.000 0的B1峰曲线重合。所以这两个图中只能见到5条曲线。前伸重叠峰的谷峰结束位置随着不对称因子AS而变,表3是图4以及表2的肩峰模式起点(谷峰模式结束点)的峰底分离度位置,由于同一图上每一条曲线的肩峰位置都不同,所以图中无法标出肩峰模式的起点(谷峰模式终点)。从这些图中可以看到,计算误差随着峰底分离度增加而减小,即误差随着重叠峰从谷峰模式进入肩峰模式而增大,最大误差在肩峰结束处。误差在肩峰模式结束处急剧增大的原因是,重叠峰即将进入完全重叠峰模式,在肩峰模式里找到的小峰峰高位置不再准确,误差增大,故式(20)计算的值误差也大。

表 2 HR=8.0和AS=2.0000的前伸重叠峰峰高和面积计算结果

图 4 峰高比HR=HA/HB=16和1.25的前伸重叠峰计算误差Fig. 4 Calculative errors of leading overlapping peaks with HR=HA/HB=16 and 1.25a. errors of peak areas; b. errors of peak heights.

ASRofHR=16RofHR=8.0RofHR=1.251.42860.50.70.72.00000.50.60.72.50000.50.50.6

3.3 拖尾峰的仿真结果比较和分析

对表1所列举的A峰和B峰,还解析了峰高比是1.25,不对称因子AS=0.500 0的拖尾重叠峰的峰高和面积,得到的结果列在表4,它们是计算结果中误差较大一组的拖尾峰数据。表4的拖尾峰峰底分离度R=0.500 0时,重叠峰进入肩峰模式。因肩峰模式所占的峰底分离度宽度较小,只有0.025,因此表4只列出了一个肩峰的计算结果。从表4中的数据可知,随着峰底分离度的减小,解析模式从谷峰模式进入肩峰模式,与前伸峰情况相同,峰高和面积的计算误差逐渐增加。在峰底分离度等于0.500 0时,解析模式进入肩峰模式。由于肩峰模式所占的峰底分离度宽度很小,因此R=0.500 0的数据也是肩峰最大误差值。虽然峰高计算误差较大,但面积误差仍然很小,面积最大误差是小峰的误差,为3.940 6% 。前面已经讨论过肩峰模式结束时,小峰的峰高位置无法准确定位,因此R=0.500 0处的峰高和面积误差急剧上升。

表 4 HR=HA/HB1=1.25和AS=0.5000的拖尾重叠峰解析峰高和面积计算结果

图5是峰高比HR=8.0的拖尾峰计算结果的误差曲线,图5b中所有A峰的误差曲线重合在一起,所以只看到4条曲线。从图5可见,AS不同但是峰高比相同的拖尾峰,它们的肩峰模式起点(谷峰模式结束点)相同。拖尾重叠峰和前伸重叠峰的解析误差规律类似,随着峰底分离度减小误差增大,肩峰模式的解析误差大于谷峰模式的解析误差。有一点差别的是,虽然最大误差都在肩峰模式里,但是有些拖尾峰,例如峰高比小的拖尾峰最大误差并不在肩峰模式的结束点,而在肩峰模式与谷峰模式的交界处附近。

图 5 峰高比HR=HA/HB2=8.0的拖尾重叠峰计算误差Fig. 5 Calculative errors of tailing overlapping peaks with HR=HA/HB2=8.0a. errors of peak areas; b. errors of peak heights.

图 6 从文献[4]图7中取得的离散数据Fig. 6 Dispersed date from the Fig. 7 in reference[4]

3.4 实验结果与计算值对比情况

图6是从文献[4]中异丙醇(isopropanol)与磷化氢(pH 3)溶液里二组分混合物5- 羟色胺(5- hydroxytryptamine,简称5ht)和5- 羟色胺酸(5- hydroxytryptophan,简称5htp)分离色谱图得到的离散数据,该数据取自文献中ED (electrochemical detection)系统的实验曲线。由于曲线拖尾过长,不能用EMG函数表示,文献[4]用GEMG函数表示单峰。

将这一组数据直接输入到作者设计的计算程序中,可得到解析后的单峰面积,计算结果见表5。表5里的计算值误差略大于GEMG解析的结果,原因如下:首先是从图上获得的数据与原始值存在一定误差;其次是数据点较少,仅有43组数据,所以数值积分有一定的误差。这两条原因增加了计算误差,但是考虑到GEMG方法需要用曲线拟合法,不能用于实时计算,而本文的算法可用于实时在线检测,这个误差还是可以接受的。

从前面的仿真与实验结果可知,解析的峰高和峰面积的误差都很小,峰面积的最大误差低于6.44% ,峰高的最大误差小于6.80% 。

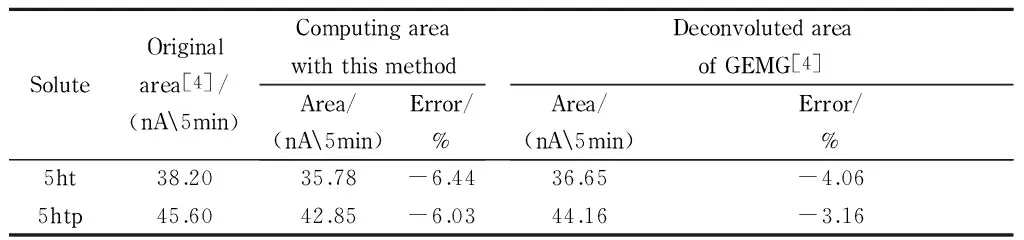
表 5 文献[4]的实验值与计算值的对比

5ht: 5- hydroxytryptamine; 5htp: 5- hydroxytryptophan. GEMG: generalised exponentially modified Gaussian function.

4 结论

本文提出了气相色谱前伸重叠峰和拖尾重叠峰的解析算法。该算法用积分方程和峰高的约束条件建立了重叠峰解析方程组,然后用数值积分和积分的渐近级数将这个方程组化成了代数方程组,再用Gauss- Seidel迭代求解了这个方程组。由于色谱解析计算时,解代数方程组的迭代次数少,解的精度高,计算效率高,所以这个算法可用于在线实时处理和色谱工作站。

[1] Liu H, Pang Z, Fan G. Chromatographia, 2016, 79: 1543

[2] Ye G Y, Xu K J. Chinese Journal of Scientific Instrument,2015, 36(2): 439

叶国阳, 徐科军. 仪器仪表学报, 2015, 36(2): 439

[3] Lin B, Lu P. J High Resolut Chromatogr Chromatogr Commun, 1987, 10(8): 449

[4] Nikitas P, Pappa Louisi A, Papageorgiou A. J Chromatogr A, 2001, 912: 13

[5] Johnsen L G, Amigo J M, Skov T, et al. J Chemometrics, 2014, 28: 71

[6] Collantes E R, Duta R, Welsh W J. Anal Chem, 1997, 69(7): 1392

[7] O’Halloran R J, Smith D E. Anal Chem, 1978, 50(9): 1391

[8] Mohammadpour K, Sohrabi M R, Jourabchi A. Talanta, 2010, 81: 1821

[9] Li B Q, Li C P, Huang Q B, et al. Journal of Chinese Mass Spectrometry Society, 2015, 36(3): 199

李宝强, 李翠萍, 黄启斌, 等. 质谱学报, 2015, 36(3): 199

[10] Dubrovkin J. Chemom Intell Lab Syst, 2016, 153: 9