基于Kolmogorov熵的边坡垂直位移预测精度研究

2018-01-10

福建质量管理 2018年1期

(1.青岛理工大学土木工程学院山东青岛 266033)

李聪明袁长丰

(1.青岛理工大学土木工程学院山东青岛266033)

针对边坡垂直位移预测效果好坏的问题，从边坡岩体的非线性特征出发，结合某岩质边坡变形监测资料，运用混沌理论分别求出各个岩体系统的Kolmogorov熵，得出了各处岩体垂直位移的有效预测的时间尺度。同时，运用混沌神经网络对各处岩体的垂直位移进行预测，通过比较各处岩体垂直位移的可预测性，分析其对边坡垂直位移预测精度的影响。结果表明：可预测性越好的岩体，其垂直位移预测精度越高，反之，预测精度越低。

Kolmogorov熵；可预测性；混沌神经网络；预测精度

一、基本理论

(一)可预测性

熵，热力学中表征物质状态的参量之一，其物理意义是体系混乱程度的度量。玻耳兹曼指出熵可以作为一个系统无序性的度量，普列戈金创立的非线性非平衡热力学得到了拓广。

Kolmogorov熵定义为信息的平均损失率：

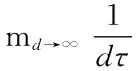
(1)

实践中，可利用K熵进行有效预测时间尺度的估计。设时刻t的信息量为I(t)，经过时间Δt后的信息量为I(t+Δt)，则有I(t+Δt)=I(t)-KΔt，取I(t)=1，则当I(t+Δt)=0时，系统的有效预测时间尺度T为

(2)

有效预测时间尺度T越短，系统的可预测性越差，反之，可预测性越好。

(二)K熵的计算

1.相空间重构

相空间重构的理论基础是Takens定理，用时间序列将系统的吸引子重建在一个未改变它拓扑结构的高维(m>D2)相空间里，其中D2为关联维数[9]。对于时间序列：x1,x2,…xn-1,xn,…，如果能适当地选定嵌入维数m和时间延迟τ，重构相空间

Y(ti)=[x(ti),x(ti+τ),x(ti+2τ),…,x(ti+(m-1)τ)](i=1,2,…)

(3)

按照Takens定理，就可以在拓扑等价的意义下保持重构m维空间中的轨线与原系统微分同胚，恢复吸引子的动力学特性[15]。

2.计算K熵

定义q阶广义熵为：

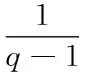
(4)

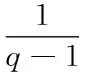
(5)

其中，K2为二阶Renyi熵，K2为Kolmogorov熵，K0为拓扑熵。已证明，K2≪K1≪K0，且通常情况下，K2是K1的一个很好的估计，故可用K2来估计K1的值。

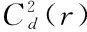
(三)混沌神经网络模型

混沌神经网络的关键步骤是将最佳嵌入维数m作为神经网络的输入层神经单元的数目，进行神经网络模型预测。

二、工程应用

(一)工程简介

某岩质边坡长约400米(道路桩号k0+000～k0+400)，坡高约10～50米。边坡岩体主要以燕山晚期粗粒花岗岩微风化带为主，边坡南部发育有后期侵入的细粒花岗岩及煌斑岩岩脉。本边坡安全等级为一级，考虑到地质条件和周边环境，采用二等边坡观测标准执行监测。

(二)边坡各监测点K熵的计算

在兼顾岩体类型的前提下，从所有的监测点中选取6个监测数据较为完整的测点作为研究对象(桩号为k0+240处边坡施工时间较晚，故其监测时间亦向后延迟)。它们的沉降监测变形曲线

进一步地通过计算坐标图m-K2中稳定的K2值，即可得到各处的K熵。图3中，计算嵌入维6-18所对应的K2值为0.013459，故K熵约为0.013459。同理，k0+80，k0+100，k0+240，k0+280，k0+320处的K熵分别约为0.012640，0.014833，0.011653，0.012269，0.013037。根据式(2)可得各监测点处边坡垂直位移的有效预测时间尺度，边坡垂直位移的有效预测时间尺度按照k0+100，k0+40，k0+320，k0+80，k0+280，k0+240的顺序依次增大，那么边坡垂直位移的可预测性也逐渐增强。

(三)边坡垂直位移的预测

利用混沌神经网络模型对边坡的垂直位移进行预测。由前文知，最佳嵌入维数m的值为12，故混沌神经网络输入层神经元的数目为12，输出层神经元数目为1，隐含层的数目通过试算最后确定为14。

预测结果误差的方差按照k0+100，k0+40，k0+320，k0+80，k0+280，k0+240的顺序依次减小，混沌神经网络模型的预测精度亦按照此顺序逐渐升高。从预测结果的平均相对误差来看，混沌神经网络模型的预测精度按照k0+100，k0+40，k0+80，k0+320，k0+280，k0+240的顺序依次升高。这里需要注意的是，k0+80的平均绝对误差略大于k0+320，而k0+80的误差的方差小于k0+320。由于预测误差的方差比平均绝对误差能更好地衡量预测的精确度，故仍然认为k0+80比k0+320的预测精度高。综上所述，混沌神经网络模型的预测精度按照k0+100，k0+40，k0+320，k0+80，k0+280，k0+240的顺序依次升高。对比上文的可预测性排序，可以看出二者的优劣程度表现出一致性，即可预测性越好，其预测精度越高，可信度也就越高。