基于ARIMA模型预测梅毒月发病率的价值

马晓梅，徐学琴，闫国立，施学忠，刘 颖，王瑾瑾，刘晓蕙，裴兰英(. 河南中医药大学公共卫生与预防学科，河南郑州 450046；. 郑州大学公共卫生学院卫生统计学教研室，河南郑州 45000)

基于ARIMA模型预测梅毒月发病率的价值

马晓梅1，徐学琴1，闫国立1，施学忠2，刘 颖1，王瑾瑾1，刘晓蕙1，裴兰英1
(1. 河南中医药大学公共卫生与预防学科，河南郑州 450046；2. 郑州大学公共卫生学院卫生统计学教研室，河南郑州 450001)

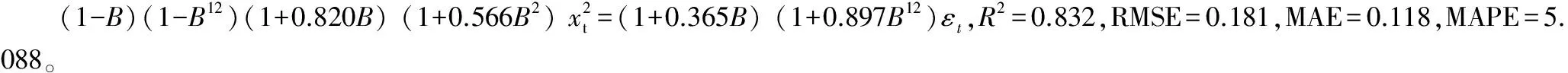
梅毒；ARIMA模型；月发病率；预测

梅毒(syphilis)是由苍白螺旋体感染引起的、主要经性接触传播的慢性传染性疾病。据国家卫生和计划生育委员会疫情最新公布信息显示，近年来，在全国报告法定传染病发病数中，梅毒始终是排前3位的病种。梅毒感染急剧增加，已成为严重的公共卫生问题，而控制该疫情发展的有效措施之一是早期预测其流行规律，给予有计划的干预管理[1]。随机时间序列分析方法中的求和自回归移动平均(auto-regressive integrated moving average, ARIMA)模型是早期预测某对象未来走势的常用方法。该模型的基本原理是利用观察值序列的自相关性，通过对模型进行定阶、检验、优化等，综合提取序列的趋势信息、周期性信息与随机波动信息等，预测其未来走势[2]。该法灵活简便、短期预测精确度高，已广泛应用于传染病的防控工作[3-5]。本研究以2009年1月-2016年6月全国梅毒月发病率数据为基础，基于ARIMA模型建模，采用实际数据验证并外推预测，分析其流行强度，以期为梅毒防控提供依据。

1 资料与方法

1.1资料来源2009年1月-2016年6月全国梅毒月发病人数资料来源于《疾病监测》和卫生部公报，2009年-2016年全国人口数来源于《中国统计年鉴》。月发病率=梅毒月发病人数/人口数×100 000。

1.2ARIMA模型ARIMA模型可以描述任何齐次非平稳时间序列，尤其适用于序列中同时存在长期趋势、周期效应和随机波动时。一般形式为：ARIMA(p,d,q)×(P,D,Q)s，其中，p和q分别为自回归和移动平均阶数，d为差分次数，P和Q为季节性自回归和季节性移动平均阶数，D为季节性差分次数，s为 季节周期和循环长度[6]。

1.3ARIMA模型的建立①平稳性检验。通过ADF(Augmented Dickey-Fuller)检验判断序列是否平稳。对于非平稳序列选择合适的差分运算使之成为平稳序列；②拟合ARMA模型。对差分后序列作相关图，考察样本自相关系数与偏自相关系数的性质对模型初步定阶，尝试确定ARMA(p,q)模型。对于含有周期变化的序列，尝试用以步长为单位的ARMA(P,Q)模型，而参数P和Q很少超过2阶，可逐个尝试；③模型检验。使用条件最小二乘法对模型参数进行估计并检验，判断参数是否有意义；对残差序列进行PortmanteauQ检验，判断是否为白噪声序列。如都满足，说明模型构建合理。如不满足任何一个，则返回第二阶段。④模型优化。根据最小信息量准则(AIC)和简洁准则，在所有通过检验的模型中AIC或BIC函数最小、拟合优度(R2)最大与参数最少的模型为相对最优模型。

1.4模型预测以2009年1月-2015年12月全国梅毒月发病率数据为基础，采用2016年1-6月实际数据验证，评定模型精度的指标为均方根误差(root mean squared error, RMSE)、平均绝对误差(mean absolute error, MAE)、平均绝对百分误差(mean absolute percentage error, MAPE)、平均相对误差(mean relative error, MRE)。之后以2009年1月-2016年6月观测值同法建模，外推预测2016年7-12月全国梅毒月发病率。限于篇幅，本研究仅列出2009年1月-2016年6月建模结果。

1.5统计学处理采用Excel 2010建立2009年1月-2016年6月全国梅毒月发病率数据库，使用Eviews 8.0软件进行ARIMA模型的识别、定阶、检验与优化，运用最优模型外推预测，检验水准α=0.05。

2 结 果

2.1梅毒月发病率(1/10万)基本情况2009年1月-2016年6月全国梅毒月发病率(xt)序列存在线性趋势和周期性波动，发病高峰集中在7-8月(图1)。

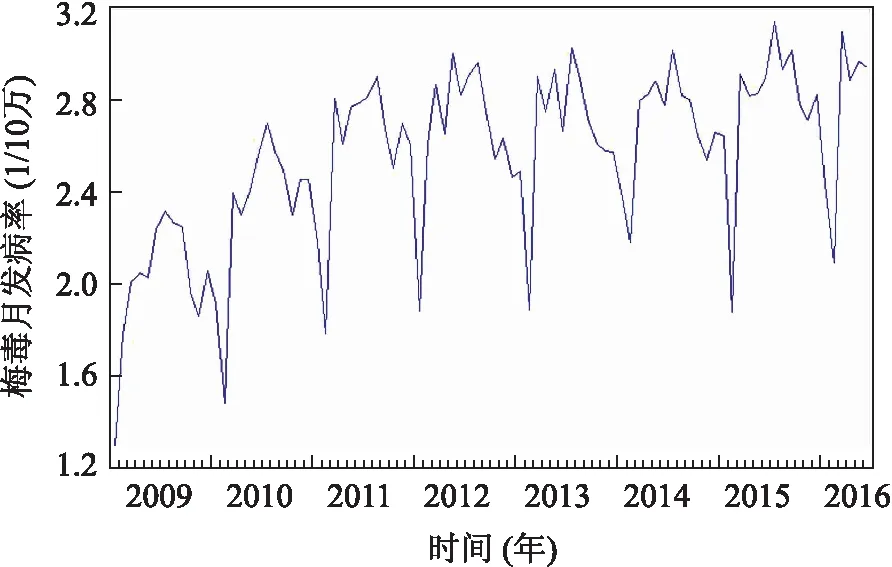
图12009年1月-2016年6月全国梅毒月发病率(1/10万)时序图

Fig.1 The sequence diagram of the monthly incidence of syphilis (1/100 000) in China from January 2009 to June 2016

2.2ARIMA模型的验证

2.2.1平稳性检验 由于存在方差波动，先对原序列进行幂转换。变换后序列经ADF检验后，2009年1月-2016年6月全国梅毒月发病率(1/10万)检验统计量为-2.610 1，P=0.277 2，该序列非平稳。1阶差分可提取趋势信息。12步差分提取周期性信息最为理想(表1)。差分后检验统计量是-11.298，P=0.000 1，为平稳序列。

2.2.2拟合ARIMA模型 该序列可以确定模型形式为ARIMA(p,1,q)×(P,1,Q)12。图2显示，自相关系数延迟1阶后衰减迅速，偏自相关系数拖尾，故尝试p=1或2，q=1。自相关系数延迟12阶非零、24阶落入2倍标准差范围，而偏自相关系数延迟12阶、24阶均落入2倍标准差范围，故P、Q尝试0或1。待拟合的备选模型：ARIMA(2,1,1)×(0,1,1)12，ARIMA(2,1,1)×(1,1,0)12，ARIMA(1,1,1)×(1,1,0)12，ARIMA(1,1,1)×(0,1,1)12。

表12009年1月-2016年6月全国梅毒月发病率(1/10万)1阶p步差分后结果

Tab.1 The one order andpstep difference results of the monthly incidence of syphilis (1/100 000) in China from January 2009 to June 2016

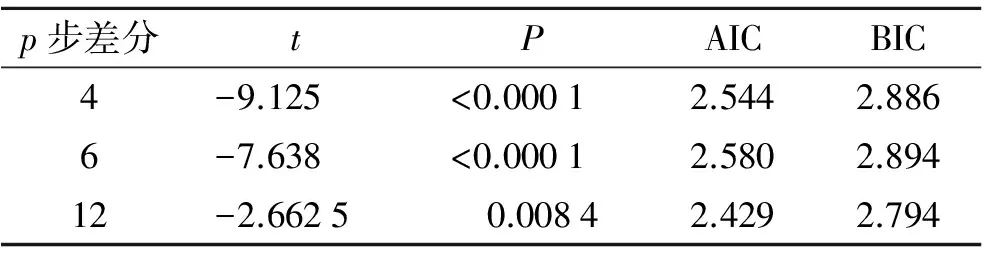
p步差分tPAICBIC4-9．125<0．00012．5442．8866-7．638<0．00012．5802．89412-2．6625 0．00842．4292．794

2.2.3模型检验 对备选模型进行参数检验，结果表明参数均有意义(表2)。对其残差进行PortmanteauQ检验，结果表明仅ARIMA(2,1,1)×(0,1,1)12和ARIMA(2,1,1)×(1,1,0)12通过白噪声序列，可用于预测(表3)。

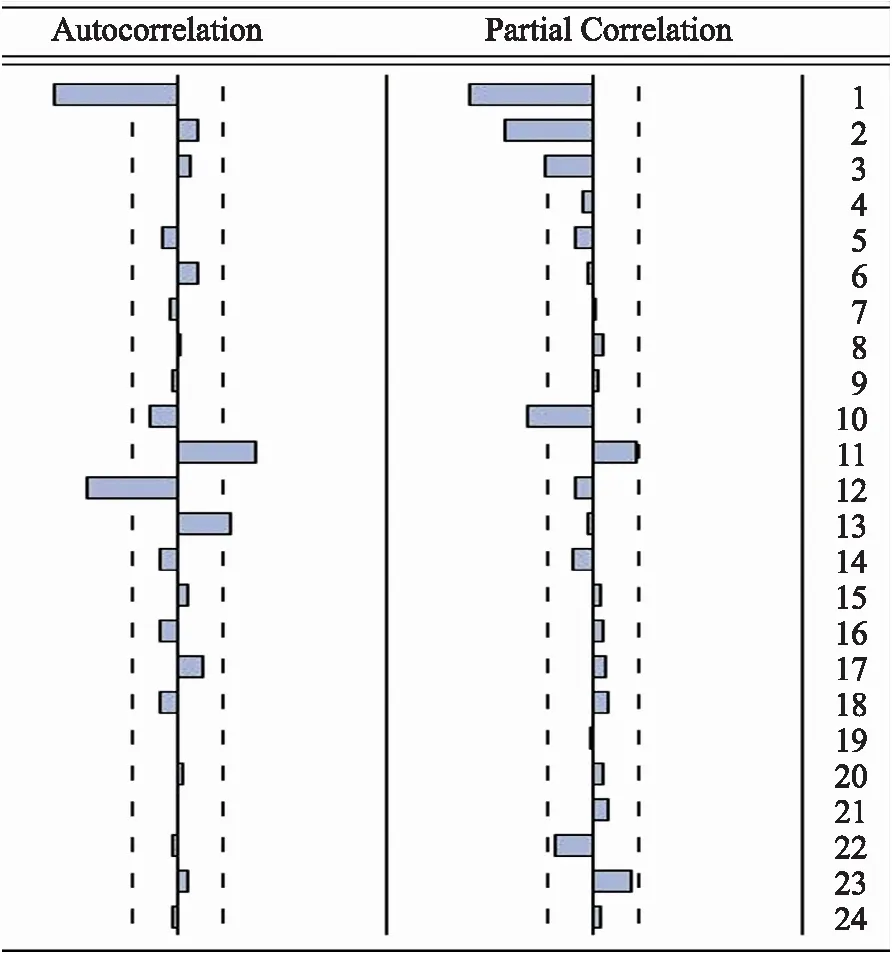
图22009年1月-2016年6月全国梅毒月发病率(1/10万)差分后序列相关图

Fig.2 The sequence diagram of the differential treatment to the monthly incidence of syphilis (1/100 000) in China from January 2009 to June 2016

表22009年1月-2016年6月全国梅毒月发病率(1/10万)备选模型检验结果

Tab.2 The estimation results of the alternative model of the monthly incidence of syphilis (1/100 000) in China from January 2009 to June 2016

表32009年1月-2016年6月全国梅毒月发病率(1/10万)备选模型PortmanteauQ检验结果

Tab.3 The alternative model estimation results of the Portmanteau Q test of the monthly incidence of syphilis (1/100 000) in China from January 2009 to June 2016

延迟阶数ARIMA(2，1，1)×(0，1，1)12QPARIMA(2，1，1)×(1，1，0)12QPARIMA(1，1，1)×(1，1，0)12QPARIMA(1，1，1)×(0，1，1)12QP6阶2．5810．2752．3390．31021．435<0．00128．538<0．00112阶10．3960．23813．1110．10831．359<0．00144．398<0．00118阶15．3470．35518．3910．19043．199<0．00157．597<0．001

2.3序列预测将最优模型以2016年1-6月实际月发病率验证，结果见表5。可见，该模型拟合值较接近于实际值，MRE=0.042，拟合效果较好。以2009年1月-2016年6月数据同法建模，外推预测2016年7-12月梅毒月发病率及其95%CI，结果见表6和图3，RMSE=0.181，MAE=0.118，MAPE=5.088。图3显示，该模型的拟合值和实际值较为吻合，且变化规律一致。

3 讨 论

近年来，时间序列分析因具有预测未来走势的应用而迅速活跃于医学和公共卫生领域[6-8]。其中，ARIMA模型是最常用、最经典的随机时间序列预测和控制的方法，其建模基本思想是利用合适差分运算实现序列平稳，然后拟合ARMA模型提取序列有效信息。该法无需考虑客观事物之间的关系及影响预测对象因素的多少，仅依据连续收集预测对象过去的统计数据，即可找到其随时间变化的规律，建立时序模型，对未来进行预测。同时可将各种影响预测对象的相关因素(包含未知因素)统一蕴含于模型之中，综合性提取序列的确定性信息(长期趋势、季节变动、循环变动等)和随机性信息，并能将其综合作用关系借助模型参数量化于具体的函数表达式中，弥补了传统回归分析法和传统时间序列分析法的不足[9]。整个建模过程步骤清晰，操作简便，短期预测结果可靠，目前广泛应用于传染病发病率的预测[10-13]。

表42009年1月-2016年6月全国梅毒月发病率(1/10万)备选模型拟合优度统计量结果

Tab.4 The alternative model estimation results of the goodness of fit test of the monthly incidence of syphilis (1/100 000) in China from January 2009 to June 2016

模型ARIMA(2，1，1)×(0，1，1)12ARIMA(2，1，1)×(1，1，0)12R20．8320．785校正R20．8250．774AIC1．8452．250BIC1．9692．386

表52016年1-6月全国梅毒月发病率(1/10万)ARIMA模型预测验证结果

Tab.5 The model of ARIMA estimation results of the monthly incidence of syphilis (1/100 000) in China from January 2016 to June 2016

月份1月2月3月4月5月6月实际值2．4322．0893．1002．8892．9662．943预测值2．4382．1703．0432．9013．0142．973绝对误差0．0060．0810．0570．0120．0480．030相对误差0．0020．0390．0180．0040．0160．010

表62016年7-12月全国梅毒月发病率(1/10万)ARIMA模型外推预测结果及95%CI

Tab.6 The model of ARIMA estimation results and 95% confidence intervals of the monthly incidence of syphilis (1/100 000) in China from July 2016 to December 2016

月份7月8月9月10月11月12月预测值3．1243．0082．9062．6912．7142．71795%CI上限3．4063．3023．2073．0153．0383．04795%CI下限2．8422．7132．6042．3682．3902．387

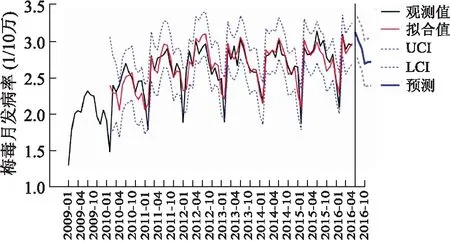
图32009年1月-2016年12月全国梅毒月发病率(1/10万)ARIMA(2,1,1)×(0,1,1)12模型拟合及预测结果

Fig.3 The predicated results of model of ARIMA (2,1,1)×(0,1,1)12of the monthly incidence of syphilis (1/100 000) in China from January 2009 to December 2016

诚然，ARIMA模型仅作为一种数学预测工具，所依据资料的样本含量有限，得到的也仅是理论值，难免会带有局限性。且随着预测时间的延长和未知信息的增多，估计的精度也会越低。因此，为达到有效预测的目的，在使用时应结合动态监测，不断更新数据对模型动态拟合，从而保持较高的预测精度，更加有效指导我国梅毒的防控工作。

[1] ZHANG X, ZHANG T, PEI J, et al. Time series modelling of syphilis incidence in China from 2005 to 2012[J]. PLoS One, 2016, 11(2):1-18.

[2] 王燕. 应用实践序列分析[M]. 第三版. 北京：中国人民大学出版社, 2014:149-197.

[3] WANG T, ZHOU Y, WANG L, et al. Using an autoregressive integrated moving average model to predict the incidence of hemorrhagic fever with renal syndrome in Zibo, China, 2004-2014[J]. Jpn J Infect Dis, 2016, 69(4):279-284.

[4] ZHANG X, PANG Y, CUI M, et al. Forecasting mortality of road traffic injuries in China using seasonal autoregressive integrated moving average model[J]. Ann Epidemiol, 2015, 25(2):101-106.

[5] LOCH H, JANCZURA J, WERON A. Ergodicity testing using an analytical formula for a dynamical functional of alpha-stable autoregressive fractionally integrated moving average processes[J]. Phys Rev E, 2016, 93(4):1-10.

[6] 范引光，吕金伟，戴色莺，等. ARIMA模型与灰色预测模型GM(1,1)在HIV感染人数预测中的应用[J]. 中华疾病控制杂志, 2012, 16(12):1100-1103.

[7] CHEN B, SUMI A, TOYODA S, et al. Time series analysis of reported cases of hand, foot, and mouth disease from 2010 to 2013 in Wuhan, China[J]. BMC Infect Dis, 2015, 15(3):1-15.

[8] 王小丽，杨永利，施学忠，等. 几种预测模型对中国梅毒发病率预测效果的比较[J]. 郑州大学学报(医学版), 2015, 50(2):164-167.

[9] 易丹辉. 统计预测：方法与应用[M]. 第二版. 北京：中国人民大学出版社, 2014:177-216.

[10] SONG X, XIAO J, DENG J, et al. Time series analysis of influenza incidence in Chinese provinces from 2004 to 2011[J]. Medicine (Baltimore), 2016, 95(26):1-7.

[11] SONG Y, WANG F, WANG B, et al. Time series analyses of hand, foot and mouth disease integrating weather variables[J]. PLoS One, 2015, 10(3):1-18.

[12] ZHANG X, ZHANG T, YOUNG AA, et al. Applications and comparisons of four time series models in epidemiological surveillance data[J]. PLoS One, 2014, 9(2):1-16.

[13] 马殿梅，王永斌，刘晓坤，等. 四种模型在我国梅毒发病率预测中的应用[J]. 中国艾滋病性病, 2016, 22(3):189-193.

ApplicationofARIMAmodelinpredictingmonthlyincidenceofsyphilis

MA Xiao-mei1, XU Xue-qin1, YAN Guo-li1, SHI Xue-zhong2, LIU Ying1, WANG Jin-jin1, LIU Xiao-hui1, PEI Lan-ying1
(1. Department of Public Health and Prevention, Henan University of Traditional Chinese Medicine, Zhengzhou 450046; 2. Department of Health Statistics,College of Public Health of Zhengzhou University, Zhengzhou 450001, China)

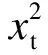
syphilis; autoregressive integrated moving average model (ARIMA); monthly incidence; prediction

2016-09-18

2017-03-15

国家“十二五”科技重大专项(No.2012ZX10004905)；河南省医学科技攻关计划项目(No.201303003)

Supported by the National “12th Five-Year Plan” Science and Technology Major Project (No.2012ZX10004905) and Henan Medical Scientific and Technological Research Project (No.201303003)

闫国立，副教授，硕士生导师. E-mail: 13937187109@qq.com

优先出版：http://kns.cnki.net/kcms/detail/61.1399.R.20171205.1811.030.html(2017-12-05)

R195.1

A

10.7652/jdyxb201801028

(编辑 卓选鹏)