筒仓中稻谷的空隙率分布研究

唐福元 许 倩 程绪铎

(南京财经大学食品科学与工程学院;江苏省现代粮食流通与安全协同创新中心, 南京 210046)

筒仓中稻谷的空隙率分布研究

唐福元 许 倩 程绪铎

(南京财经大学食品科学与工程学院;江苏省现代粮食流通与安全协同创新中心, 南京 210046)

采用LHT-1粮食回弹模量仪测定稻谷(南粳5055)堆的表层密度及压缩密度，建立筒仓中稻谷堆的密度、应力与粮层深度关系的微分方程组，用数值方法计算筒仓中稻谷密度与粮层深度关系。采用粮食孔隙率测量仪测定表层稻谷(无压缩)孔隙率，由表层孔隙率，表层密度及筒仓深处的密度计算出筒仓中稻谷孔隙率与粮层深度关系。计算结果表明：在直径20米的筒仓中，在30米的筒体部分，南粳5055空隙率变化范围为61.00%～56.32%，在10 m的锥斗中，空隙率变化范围为56.32%～59.77%；在带锥斗筒仓的筒体部分，稻谷堆孔隙率随着粮层深度的增加而减小；到锥斗部分，稻谷堆孔隙率随着粮层深度的增加而逐渐增大。在不同直径的筒仓的筒体部分，在同一深度，稻谷堆孔隙率随着筒仓直径的增大而减小。

筒仓 稻谷 孔隙率 密度

稻谷是我国单产最高、总产最多的粮食作物，在国家粮食供应与安全中具有重要的地位[1]。筒仓是储粮仓型中机械化程度最高的一种仓型，被广泛应用于稻谷的储藏[2-3]。稻谷储藏在筒仓中，受到自重、内摩擦力以及仓壁的支持力，稻谷堆的各处产生压应力与切应力，从而产生体积应变与形状应变，体积缩小，密度增大，孔隙率减小。随着粮层深度的增加，稻谷的密度增大[4-5]，孔隙率减小。准确地计算出筒仓中粮堆孔隙率的分布值能给筒仓中粮堆各处的通风阻力的计算提供技术参数。 粮堆的孔隙率的分布还影响粮堆中的热量与水分的迁移。因此，计算出筒仓中孔隙率的分布值对粮食安全储藏具有重要意义。

粮食孔隙率的测定始于二十世纪六十年代[6]。早在1967年Thompson等[6]使用气体比重瓶测定了燕麦、小麦、高粱、大豆、黑麦、大麦、玉米和紫花苜蓿种子的孔隙率，但是他们测定的样品容积只有50 mL。Gustafson[7]使用气体比重瓶测定了玉米的孔隙率。 Chang[8]使用气体比重瓶测定了不同含水率的玉米、小麦和高粱的孔隙率。目前测定粮食孔隙率的方法是气体置换法，其测定装置主要有定容型[9]、变容型[10]和比较型[11]。这些装置的容积都很小(5 L以下)，只能测量小粮堆(5 L以下)的孔隙率，不能测定粮仓内粮堆孔隙率。郝倩等[12]自制小仓测定了仓内小麦、玉米的孔隙率，该仓的容积只有50 L，测定的只是小麦和玉米的平均孔隙率。测定孔隙率还有光学法[13-18]、声学法[19]等，这些方法也不适合用来测定粮仓内粮堆孔隙率。

由于筒仓中的粮堆结构的复杂性，揭示粮仓中粮堆的孔隙率的分布是个难题。到目前为止，粮仓中粮堆的孔隙率分布的理论与试验成果鲜有报道。本研究采用LHT-1粮食回弹模量仪来测定出稻谷堆压缩密度，建立筒仓中稻谷堆的密度、压应力与粮层深度关系的微分方程组，用数值方法计算得到筒仓中稻谷密度随粮层深度变化关系，再由表层孔隙率，表层密度及筒仓深处的密度计算出筒仓中稻谷孔隙率与粮层深度关系。

1 材料与方法

1.1 试验材料

南粳5055稻谷，原始含水率为12.95% (湿基)，2016年产于南京。2016年11月至12月进行压缩试验。

试验时，将其含水率调节为11.77%、12.95%、14.47%、15.75%、17.58% w.b.。稻谷籽粒的最大直径、中直径、最小直径的平均值分别为6.8、3.4、2.3 mm，对应的标准差分别为0.2、0.2、0.1 mm。(随机取样100粒稻谷粒，用游标卡尺测得其3个粒径，精确到0.1 mm，最后求其平均值。)

1.2 试验仪器

LHT-1型粮食回弹模量测定仪：南京土壤仪器厂有限公司；LKY-1型粮食孔隙率测定仪：南京土壤仪器厂有限公司；HG202-2(2A/2AD)电热干燥箱：南京盈鑫实验仪器有限公司。

1.3 试验方法

1.3.1 稻谷堆压缩密度的测定

将稻谷装入LHT-1粮食回弹模量仪的圆筒中，顶部施加压力，筒壁对稻谷产生向上的摩擦力，装样筒内各粮层所受到的竖直应力与侧向应力不同。 本试验用圆筒中稻谷的平均竖直应力与侧向应力表示筒仓中某一粮层的竖直应力与侧向应力。

采用微元法对装样筒内粮堆样品进行受力分析，假设装样筒内半径为Rc，压缩样品高度为Hc，取距离粮面深度为y，高度为dy的微元体进行受力分析[5]，微元体在竖直方向的受力分析见图1：

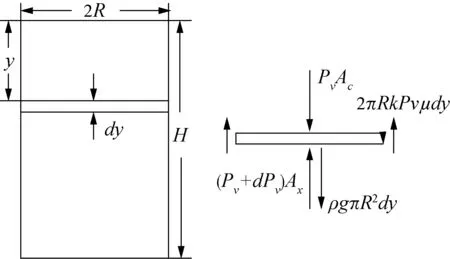
图1 回弹模量仪装样筒中粮堆微元层受力图

稻谷在装样筒内受压时处于主动应力状态，根据Rankine理论，侧向应力与竖直应力的比为：

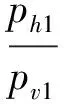
(1)

式中：ph1为圆筒中粮堆所受侧向应力/kPa；pv1为圆筒中粮堆所受竖直应力/kPa；φ为稻谷内摩擦角/°。

粮堆微元体在竖直方向上受力平衡，可得平衡方程为：

(2)

式中：ρ为稻谷密度/kg/m3；μc为稻谷与装样筒筒壁的摩擦系数；Ac为装样筒的横截面积/m2。

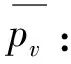
(3)

式中：p0为粮堆顶部压应力/kPa。

在装入稻谷的圆筒顶部逐级加载，测定每次加载后稻谷样品的高度，计算出对应的稻谷密度，并根据式(3)计算出对应的竖直应力，即可得到稻谷样品密度与其所受竖直应力(最大主应力)的关系:

ρ=F(pmax)

(4)

将回弹模量仪放在实验室中，室内温度设置为20 ℃。将样品匀速倒入装样筒中，并将其表面铺平，放上传压板，保证传压板上表面与装样筒上端齐平。保持横梁杠杆垂直，转动平衡锤调整杠杆至水平以上，用M16螺母固定平衡锤。旋转传压螺钉与传压板接触，调整0～30 mm位移传感器的触头位置，调零百分表。根据试验要求，对试样进行加载。随着试样的下沉，杠杆向下倾斜，为防止杠杆倾斜影响加载精度，调节调平手轮，使杠杆处于水平位置。试验进行3 d后记录样品高度，计算样品压缩后的体积，结束试验，倒出装样筒内的稻谷样品，称重并记录稻谷质量。稻谷堆的密度即为稻谷的质量除以压缩后的体积[5]。

1.3.2 稻谷堆表层孔隙率测定

粮食孔隙率ε为粮食中孔隙与粮堆体积之比。本试验使用LKY-1型粮食孔隙率测定仪(见图2)测定表层稻谷的孔隙率。

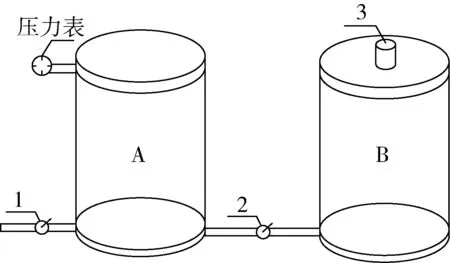
图2 孔隙率测定仪示意图

如图2所示，两个容积相等的压力容器A和B，在容器B中装满样品并将其密封。关闭阀门2，打开阀门1、3，用空气压缩机向容器A中鼓入一定压力的气体。当压力表指针达到一定数值时，关闭阀门1，当压力值稳定后，记下压力表读数P1；关闭阀门3，然后打开阀门2，当容器A和B中压力平衡时，记下此时压力表读数P2。视空气为理想气体，由理想气体等温过程的特性推出孔隙率如下：

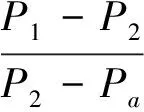
1.4 筒仓内稻谷密度、压应力与粮层深度关系的微分方程组的构建

设带锥斗筒仓的直径为D，圆筒高为H，锥斗高为h，锥斗壁与水平面夹角为α，稻谷的内摩擦角为φ，仓墙与稻谷间的摩擦系数为μ，设水平压应力与竖直应力大小不随半径的大小和方向而变化。带锥斗的筒仓和稻谷表面下深度y处稻谷的微元层受力示意图如图3所示。

筒体部分，其微元层的受力如图3b所示。微元层在竖直方向上合力为零，则得到：

(pv+dpv)A+μphCdy-pvA-ρgAdy=0

(5)

式中：pv为稻谷竖直应力/kPa；ph为侧应压力/kPa；ρ为稻谷的密度/kg/m3；g为重力加速度/m/s-2；A为圆筒的横截面面积/m2；C为圆筒的周长/m；且

C=A/R

(6)

式中：R为水力半径/m；R=D/4。

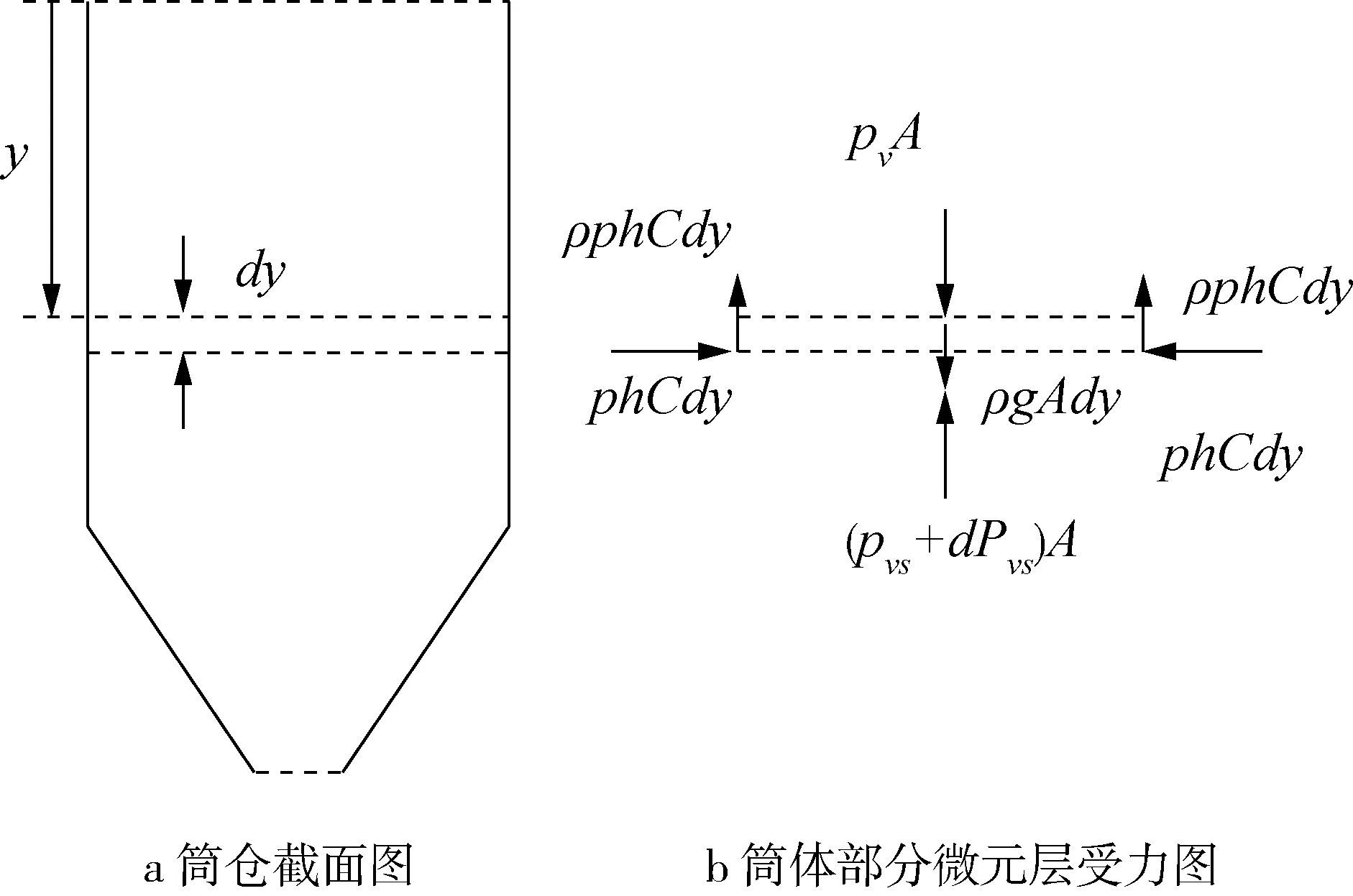
图3 筒仓的筒体中微元体受力图

稻谷储藏在筒仓中，稻谷处于主动应力状态，稻谷最小主应力(即筒壁侧压力ph)和最大主应力(即竖直应力pv)之比k为：

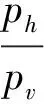
(7)

结合式(5) ～ (7)得到筒体部分最大主应力pv的微分方程：

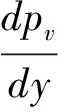
(8)

锥斗部分，其截面图和微元层受力如图4所示。在同一水平面上的锥斗部分微元层，其粮堆的最大主应力的大小与方向都是变化的。在锥斗壁处稻谷处于被动应力状态，此处最大主应力方向垂直于锥斗壁。筒体底层中心的最大主应力与锥斗顶面中心最大主应力是相等的。锥斗内的任一水平微元层,中心竖直应力(pvc)是该处的最大主应力，边缘竖直应力并不是该处的最大主应力，也不是该处的最小主应力，在锥斗壁处(微元层边缘处)取一微元体如图4b、4c 所示，微元体受到的最大和最小压应力分别为phmax和phmin，phmax为锥斗壁侧压力，且微元体的最小压应力和最大压应力之比为k。

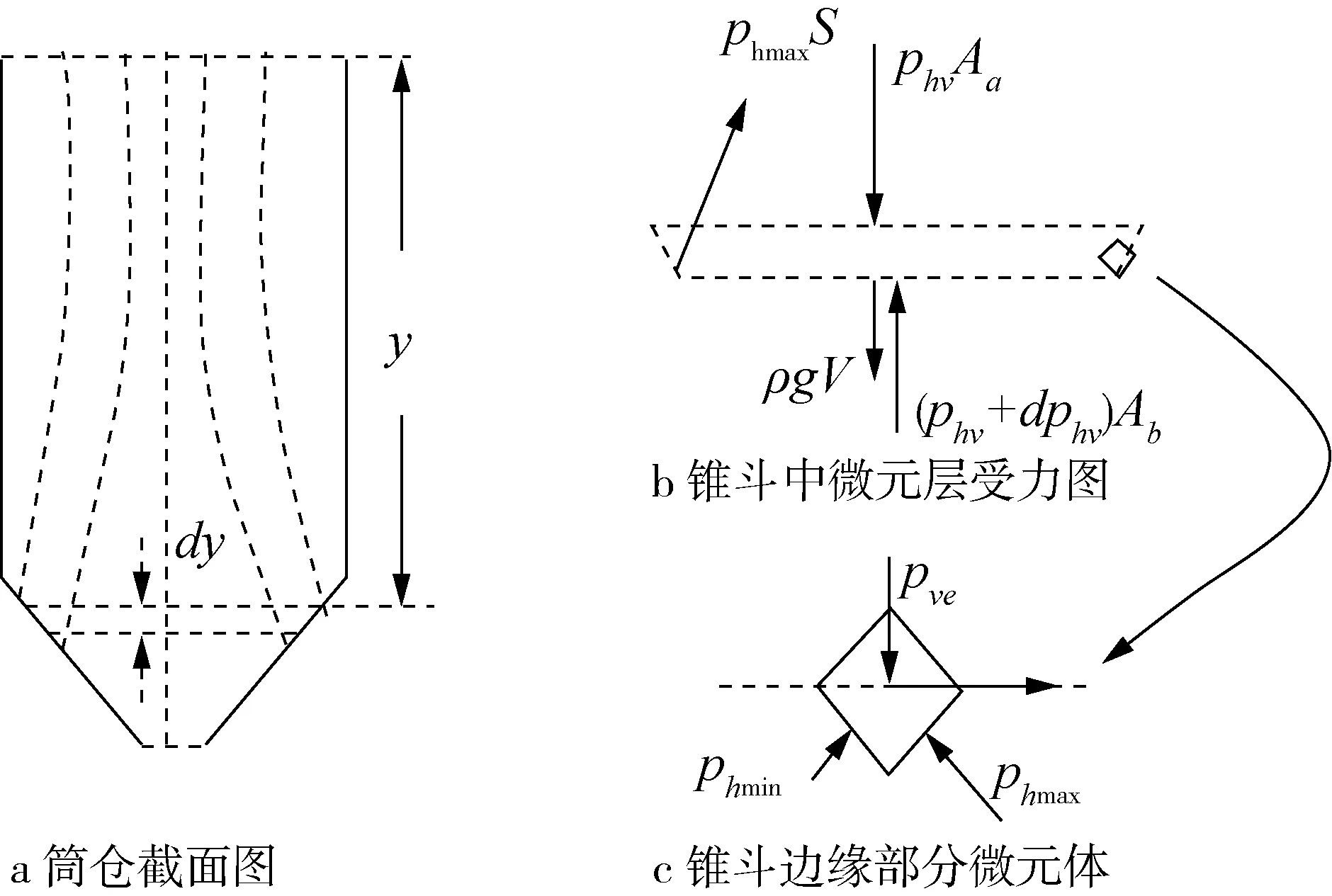
图4 筒仓锥斗部分微元体受力图

根据Rankine压力理论得到水平稻谷薄层边缘处竖直应力pve：

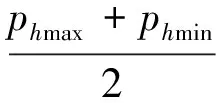
(9)

令

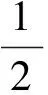
(10)

同一水平微元层的竖直应力取平均值phv：

phv=(pve+pvc)/2=(λ+1)phmax/2

(11)

作用于微元层上竖直方向的合力等于0：

phvAa+ρgV-(phv+dphv)Ab-phmaxScosα=0

(12)

式中：Aa为上底面的面积/m-2；Ab为下底面的面积/m-2；S为侧表面积/m-2；V为微元体的体积/m-2。

设水平面上稻谷薄层的半径为r，则

Aa=πr2

(13)

Ab=π(r-dycotα)2=π(r2-2rcotαdy)

(14)

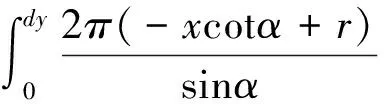
(15)

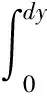
(16)

结合(9) ～ (16)式并化简得到锥斗部分最大主应力(锥斗壁侧压应力)方程：

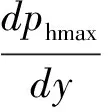
(17)

结合式(7)、(8)、(4)得到筒体部分压应力、密度与粮层深度关系的方程组：

(18)

结合式(10)、(11)、(17)、(4)得到锥斗部分压应力、密度与粮层深度关系的方程组：

(19)

式中：phv为锥斗中粮堆竖直应力/kPa；phmax为锥斗壁侧压应力/kPa。

方程组(18)、(19)的连续条件为：

pv(H)=phmax(H)

(20)

方程组(18)、(19)的边界条件为：

(21)

1.5 方程组(18)～(21)数值计算步骤

1.5.1 筒仓中稻谷堆分层

筒仓中稻谷堆分为n层, 筒体中n1层，漏斗中n2层。每层的厚度(高)为dy, 层数为：n1=H1/dy;n2=H2/dy; n=n1+n2。其中，H1为筒体的高，H2为锥斗的高。

1.5.2 第一层密度与竖直压应力

依据方程21得，ρ1=ρ0(表层密度),pv,1=0 (表层竖直压应力)。

1.5.3 计算筒体中第2层到第n1的压应力与密度

a.由方程组18的第3式计算压应力增量dp；

b.计算下一层压应力：(pv)next layer= (pv)current layer+dp；

c.由方程组18的第1式计算该层密度。

1.5.4 计算漏斗中各层的压应力与密度

a.由方程(20)知，漏斗中第1层的最大主应力等于筒体中最下层的竖直压应力；

b.由方程组19的第2式计算压应力增量dphmax；

c.计算下一层主应力：(phmax)next layer= (phmax)current layer+dphmax

d.由方程组19的第1式计算该层密度。

1.6 粮食孔隙率与密度的转换关系

粮堆表层孔隙率为：

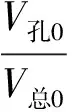
(22)

由(22)可得:

(23)

粮堆深层密度为：

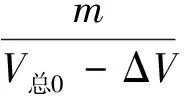
(24)

由(24)得：

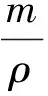
(25)

粮堆深层孔隙率为：

(26)

式中：e0为表层孔隙率，e为粮堆孔隙率，V孔为孔隙的体积/m3；m为粮堆质量/kg；V总0为粮堆总体积/m3；ρ为粮堆密度/kg/m3；ρ0为粮堆表层密度/kg/m3。

2 结果与分析

2.1 稻谷堆竖直压应力与压缩密度

2.1.1 稻谷堆竖直压应力

由直剪仪测得南京5055稻谷的内摩擦角和摩擦系数的试验结果见表1。

表1 不同竖直压应力下稻谷的内摩擦角和摩擦系数

使用回弹模量仪通过逐级加载的方式对稻谷堆进行压缩试验，加载的顶部竖直应力分别为50、100、150、200、250、300 kPa。根据表1中的参数与试验测定的样品压缩的顶部压力与样品高度，根据式(3)计算得到稻谷堆所受的平均竖直应力，结果见表2。

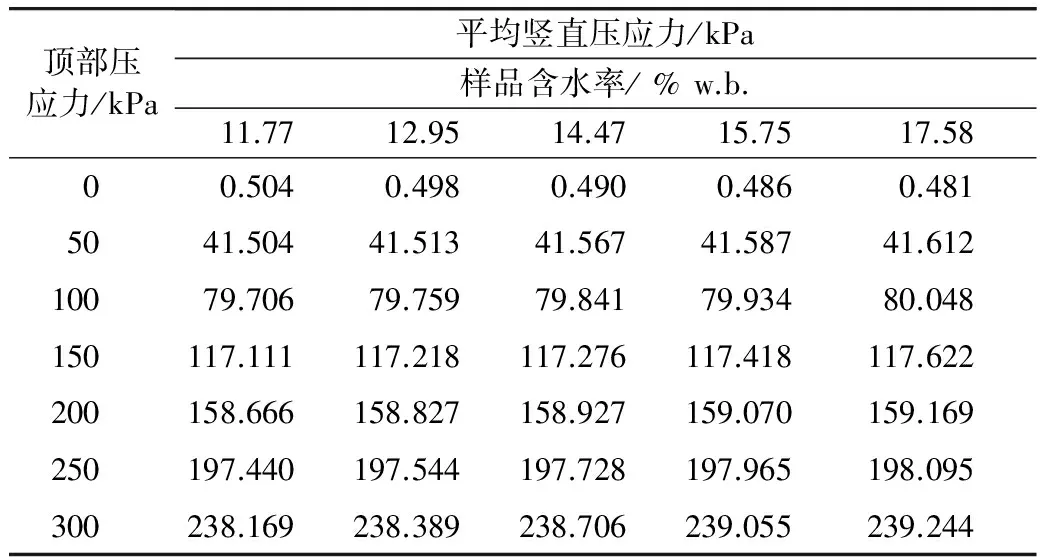
表2 不同含水率、不同顶部压力下的稻谷堆所受的平均竖直压应力

2.1.2 稻谷堆的压缩密度

不同含水率、不同顶部压应力下的稻谷堆压缩后测定的密度见表3。

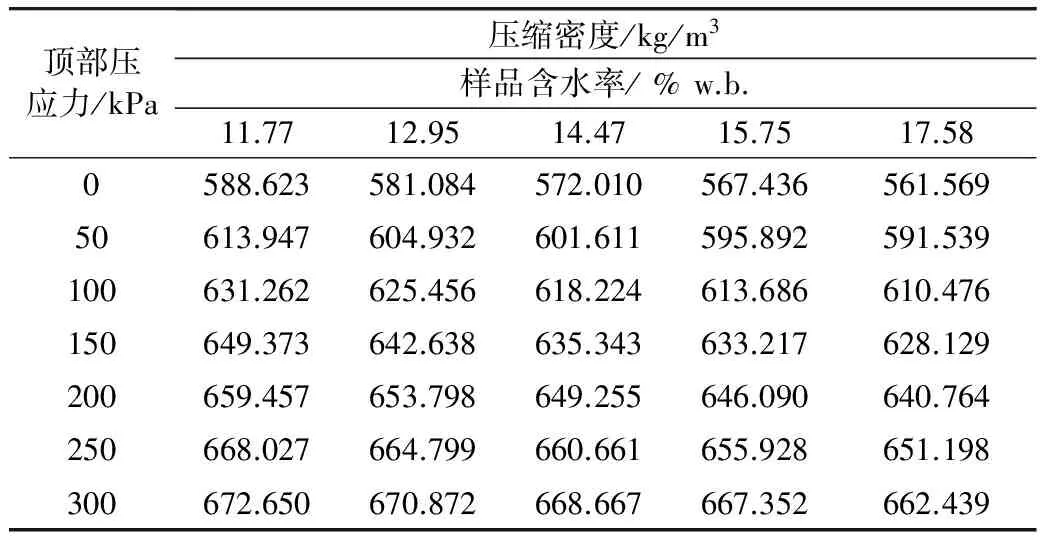
表3 不同含水率、不同顶部压力下的稻谷堆的压缩密度

2.2 表层稻谷孔隙率

粮食孔隙率测定仪测定出南粳5055(含水率12.95% w.b.)表层稻谷孔隙率e0为0.610 0，标准差为0.000 3。

2.3 稻谷堆压缩密度与平均竖直应力的关系

由表2和表3拟合稻谷堆密度与平均竖直应力的关系方程为ρ=apv2+bpv+c[ρ=F(pmax)]，其中，pv为竖直压应力，为压缩密度，pmax为最大主应力，方程系数a、b、c随含水率的变化而变化，结果见表4。

表4 稻谷堆密度与平均竖直压应力的拟合方程系数

2.4 筒仓中稻谷堆密度与粮层深度的关系

设筒仓的参数条件如表5所示。

表5 筒仓的参数

储藏稻谷的含水率为12.9%，内摩擦角为40°，与仓壁的摩擦系数为0.4，表面密度为560 kg/m3。顶部粮面水平，选择粮堆的每一薄层为0.1 m。数值法求解微分方程组(18) 和(19)，从而计算得到不同粮层深度下稻谷堆的密度,如表6所示。

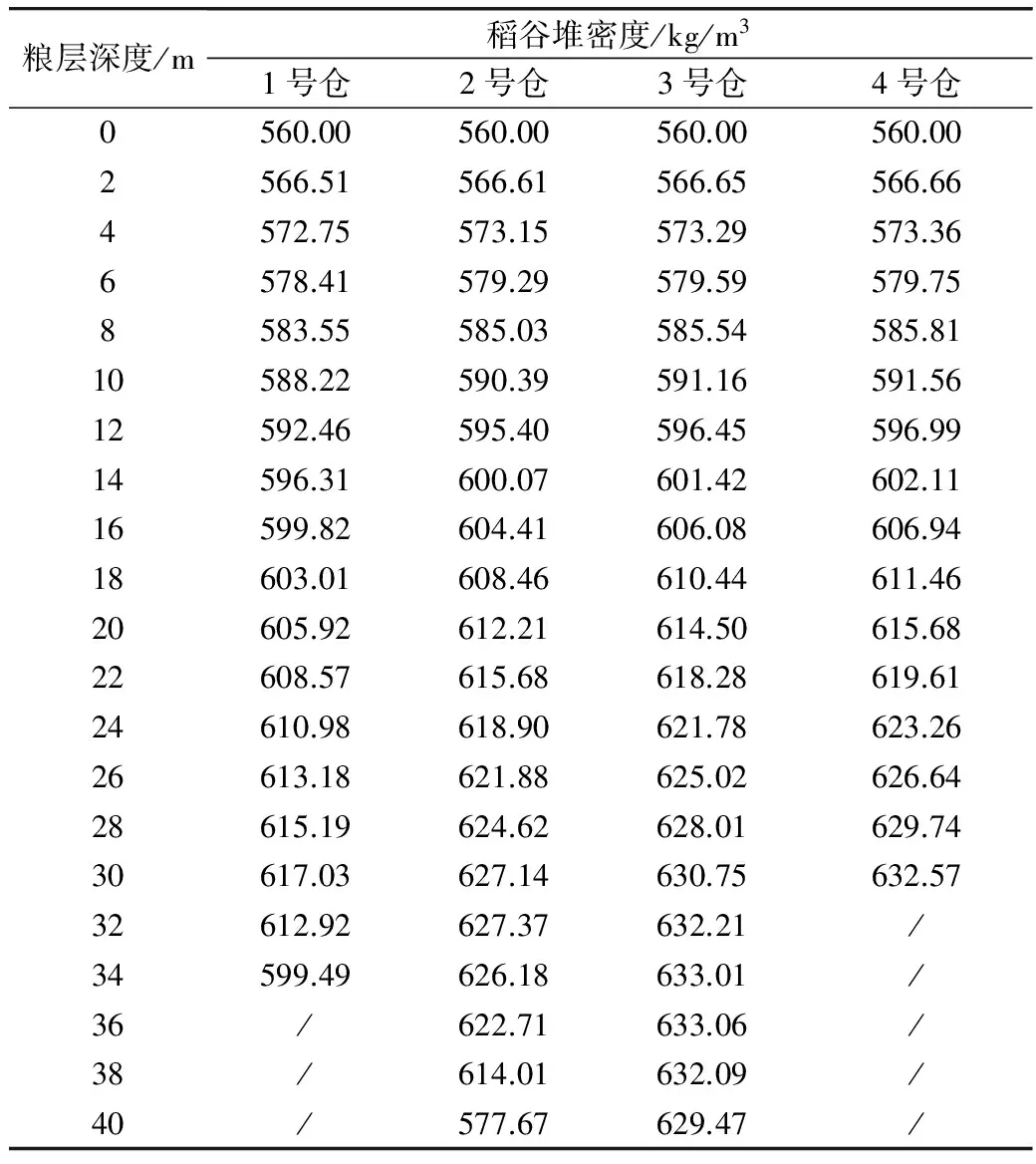
表6 不同粮层深度下稻谷堆的密度

由表6知，在筒仓的筒体部分，稻谷密度随着粮层深度的增加而增增加；在锥斗部分，随着粮层深度的增加，稻谷堆密度逐渐减小。

2.5 筒仓中稻谷堆孔隙率与粮层深度的关系

选定筒仓的参数如表5所示，选定稻谷是南粳5055，2015年产于南京，稻谷的含水率为12.9% w.b.，其内摩擦角为40°，与仓壁的摩擦系数为0.4，稻谷的表面密度为560 kg/m3。

表层孔隙率e0可按1.2试验方法测得，表层密度ρ0可按1.1试验方法测得，经过公式(26)的转换可以由稻谷堆密度(表6)计算出筒仓内稻谷堆孔隙率与粮层深度的关系，如表7所示。表6与表7的结果密切相关，密度大处孔隙率就小。

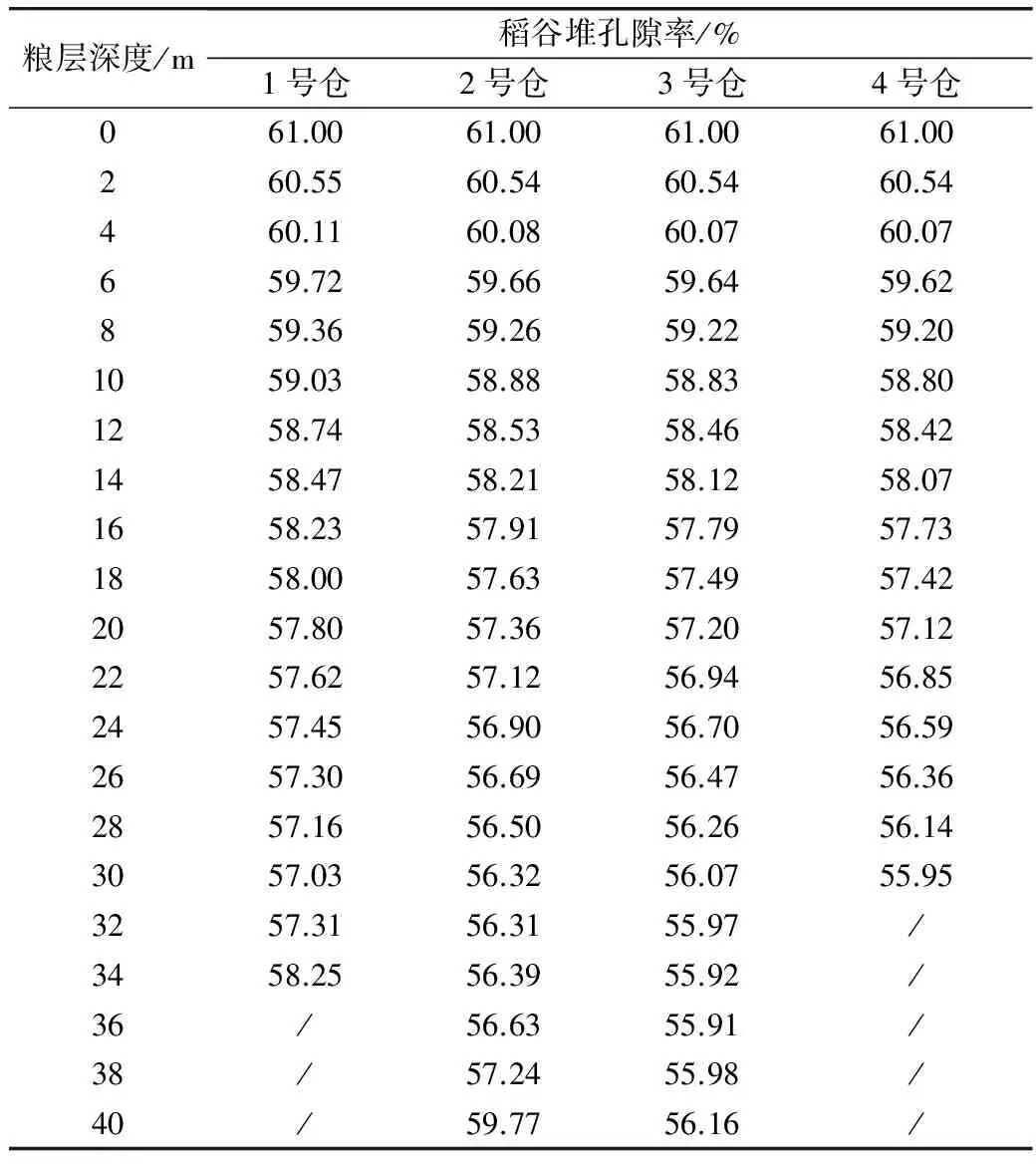
表7 不同粮层深度下稻谷堆的孔隙率

由表7可知，在直径10米的筒仓中，在30米的筒体部分，南粳5055空隙率变化范围为61.00%～57.03%，在5米的锥斗中，空隙率变化范围为57.03%～58.25%；在直径20米的筒仓中，在30米的筒体部分，南粳5055空隙率变化范围为 61.00%～56.32%，在10米的锥斗中，空隙率变化范围为56.32%～59.77%；在直径40米的筒仓中，在30米的筒体部分，南粳5055空隙率变化范围为61.00%～55.95%。

在筒仓的筒体部分，稻谷堆孔隙率随着粮层深度的增加而增减小，这是由于压应力随着粮层深度的增加而增加的缘故。在锥斗部分，随着粮层深度的增加，稻谷堆孔隙率逐渐增大；这是由于压应力随着粮层深度的增加而增加的缘故。在不同直径的筒仓的筒体部分，在同一深度，稻谷堆孔隙率随着筒仓直径的增大而减小。这是由于在同一深度，稻谷堆压应力随着筒仓直径的增大而增大的缘故。

3 结论

3.1 在筒仓的筒体部分，稻谷密度随着粮层深度的增加而增增加；在锥斗部分，随着粮层深度的增加，稻谷堆密度逐渐减小。

3.2 在直径20 m的筒仓中，在30米的筒体部分，南粳5055空隙率变化范围为61.00%～56.32%，在10米的锥斗中，空隙率变化范围为56.32%～59.77%。

3.3 在筒仓的筒体部分，稻谷堆孔隙率随着粮层深度的增加而增减小；在锥斗部分，随着粮层深度的增加，稻谷堆孔隙率逐渐增大。

3.4 在不同直径的筒仓的筒体部分，在同一深度，稻谷堆孔隙率随着筒仓直径的增大而减小。

[1]王瑞元，朱永义，谢健，等. 我国稻谷业加工现状与展望[J]. 粮食与饲料工业, 2011 (3): 1-5

Wang Ruiyuan, Zhu Yongyi, Xie Jian, et al. Present situation andprospect of rice processing in China [J]. Food and Feed Industry, 2011 (3): 1-5

[2]张承光. 现代化储粮仓型的选择[J]. 粮油仓储科技通讯, 2002 (2): 42-44

Zhang Chengguang. Selection of modern granary type [J]. Grain and Oil Storage Science and Technology, 2002 (2): 42-44

[3]曾丁,黄文彬,华云龙. 筒仓壁压的有限元分析[J].农业工程学报, 1998, 14 (2): 44-48

Zeng Ding, Huang Wenbin, Hua Yunlong. Finite element analysis of silo wall pressure [J]. Journal of Agricultural Engineering, 1998, 14 (2): 44-48

[4]石翠霞. 筒仓内小麦、玉米堆的压缩特性、仓壁压应力及储粮总重量的研究[D].南京:南京财经大学, 2011

Shi Cuixia. Compression characteristics of wheat and corn pile，compressive stress of silo wall and total weight of stored grain in silo [D]. Nanjing: Nanjing University of Finances and Economics, 2011

[5]严晓婕.稻谷堆与籽粒的压缩特性及其在筒仓中密度与应力分布的研究[D].南京:南京财经大学, 2014

Yan Xiaojie. Compression characteristics of rice paddy and grain and their density and stress distribution in a silo [D]. Nanjing: Nanjing University of Finances and Economics, 2014

[6] Thompson R A, Isaacs G W. Porosity determination of grains and seeds with an air-comparision pycnometer [J]. Trans. ASAE, 1967, 10(2):693-696

[7] Gustafson R J. Density and porosity changes of shelled corn during drying[J]. Trans. ASAE, 1972, 15(2):523-527

[8] Chang C S. Measuring Density and Porosity of Grain Kernels Using a Gas Pycnometer [J]. Cereal Chemistry.1988,65(1):13-15

[9] 张淑珍，巴卫国，徐宝江，等． 散粒物料孔隙率测定装置的研制[J]. 农业工程学报，1996,12(1):187-191

Zhang Shuzhen, Ba Weiguo, Xu baojiang, et al. granular material porosity determination device [J]. Journal of Agricultural Engineering, 1996,12 (1): 187-191

[10] Marinder B O. A simple apparatus for determining the density of solids[J]. Measurement Science & Technology,1996,7(11) :1569-1573．

[11] Bielders C L，Debacker L W，Delvaux B. Particle density of volcanic soils as measured with a gas pycnometer[J]. Soil Science,1990,54(3) : 822-826

[12] 郝倩，陈弘毅，平学文，等. 一种新型粮食孔隙度就仓测量系统研究[J]. 农机化研究，2015,9:180-184

Hao Qian, Chen Hongyi,Ping Xuewen, et al. Research on a new grain porosity measurement system [J]. Agricultural Mechanization Research, 2015,9:180-184

[13] Cheng J, Sun W. Automatic measurement of pores and porosity in pork ham and their correlations with processing time,water content and texture[J]. Meat science,2006,72(2) : 294-302

[14] Mang J T, Hjelm R P, Francois E G. Measurement of porosity in a composite high explosive as a function of pressing conditions by ultra-small-angle neutron scattering with contrast variation[J]. Propellants, Explosives,Pyrotechnics,2010,35(1): 7-14

[15] Yao Y, Liu D. Comparison of low- field NMR and mercury intrusion porosimetry in characterizing pore size distributions of coals[J]. Fuel,2012,95: 152-158

[16] Nippolainen E, Tuomas E, Ketolainen J, et al. Measuring tablet porosity using multispectral imaging system[J]. Optical Review,2010,17(3) : 323- 326

[17] Podymova N, Karabutov A, Kobeleva L, et al. Laser optoacoustic method of local porosity measurement of particles reinforced composites[J]. Journal of Physics Conference Series,2011, 278(1) : 12-38

[18] Hogekamp S, Pohl M. Porosity measurement of fragile agglomerates[J]. Powder Technology, 2003,130(1-3):385-392

[19] Umnova O, Chul H, Cummings A. Deduction of tortuosity and porosity from acoustic reflection and transmission measurements on thick samples of rigid-porous materials[J]. Applied Acoustics,2005,66(6):607-624.

Research on Porosity Distribution of Paddy in Silos

Tang Fuyuan Xu Qian Cheng Xuduo
(College of Food Science and Engineering, Nanjing University of Finance and Economics/Collaborative Innovation Center for Modern Grain Circulation and Safety, Nanjing 210046)

The LHT-1 rebound modulus tester was used to determine the compression density of paddy(South japonica5055). The differential equations of density，pressure and depth in a silo was built. Numerical method was used to obtain the relationship of density and depth. The porosity of surface layer of paddy (no compression) was measured by grain porosity meter. According to the porosity of surface layer, the density of surface layer and densities calculated in the silo, the relation between grain porosity and grain depth in silo was calculated. Calculation results show that in the 30 meter cylinder part of a silo with a diameter of 20 meters, the change range of the porosity of South japonica5055 paddy is 61.00%～56.32%, and in the cone hopper of 10 meters of the silo, the change range of porosity is 56.32%～59.77%; in a silo with a cone hopper, porosity of paddy in cylinder of silo decreased with the paddy depth, the porosity of paddy in cone hopper increased with the increase of depth. At the same depth, the porosity of paddy decreases with the increase of silo diameter.

silo, paddy, porosity, density

TS210.4

A

1003-0174(2017)12-0110-07

时间：2017-12-20 17:02:53

网络出版地址：http://kns.cnki.net/kcms/detail/11.2864.TS.20171220.1702.002.html

国家自然科学基金(31371856)，江苏高校优势学科建设工程(PAPD)

2017-06-22

唐福元,男,1962年出生,副教授,粮食储藏工程

程绪铎,男,1957年出生,教授,粮食储藏工程