非金属非粘结软管拉伸性能的数值模拟分析
2018-01-10,,,
,,,
(1.国家海洋局第二海洋研究所 工程海洋学重点实验室,杭州 310012;2.中国海洋大学 山东省海洋工程重点实验室,山东 青岛 266100)
非金属非粘结软管拉伸性能的数值模拟分析
周阳1,黄维平2,张艳君2,俞亮亮1
(1.国家海洋局第二海洋研究所 工程海洋学重点实验室,杭州 310012;2.中国海洋大学 山东省海洋工程重点实验室,山东 青岛 266100)
针对非金属非粘结软管在拉伸状态下的力学特性,采用ABAQUS对其进行有限元分析并充分考虑了对层与层之间的摩擦接触。研究表明,提高抗压层扁带的环向强度、抗拉层扁带的轴向拉伸强度及环向拉伸强度可以提高软管的抗拉性能;抗拉层螺旋缠绕角和抗拉层厚度对软管拉伸刚度的影响较大,而内外压、抗拉层扁带数量和摩擦系数对软管拉伸刚度的影响很小。
非金属非粘结软管;有限元分析;摩擦接触;ABAQUS;拉伸刚度
海洋软管按制造工艺,可以分为粘结软管和非粘结软管。按增强层所用材料区分,海洋软管也可以分为金属软管和非金属软管,其中金属软管的增强层采用金属材料,以碳钢居多,而非金属软管的增强层则采用纤维增强树脂基复合材料。目前对非粘结软管的研究主要采用有限元数值模拟、模型试验和理论模型解析分析。研究内容一般包括单一荷载和组合荷载作用下软管的力学特性分析[1-5],对金属软管的研究,一般采用数值模拟和解析模型相互验证的方法,也有引入实验进行验证的[6-9],而对非金属软管的理论分析、设计、生产及建造的相关研究工作非常少,尤其对于力学性能的研究更不完善[10-14],很少对非金属软管结构的各种设计参数对力学性能的影响进行研究。为此,考虑采用数值模拟和解析模型相互验证的方法,分析非金属软管的拉伸性能。
1 数值建模
1.1 有限元模型
图1是一个非金属非粘结软管的有限元模型,共分为5层,螺旋扁带层的缠绕角为α,见图2。内衬层和外套层都采用尼龙PA11,在深水环境中,PA11优于HDPE等其他材料,可作为内衬层和外套层使用,同时具有耐高温和耐低温性,而且有不错的抗磨损和抗疲劳性能[15]。抗拉层螺旋扁带和抗压层螺旋扁带都采用玻璃钢(纤维增强树脂基复合材料)。软管的几何尺寸见表1,材料常数见表2。

图1 软管模型
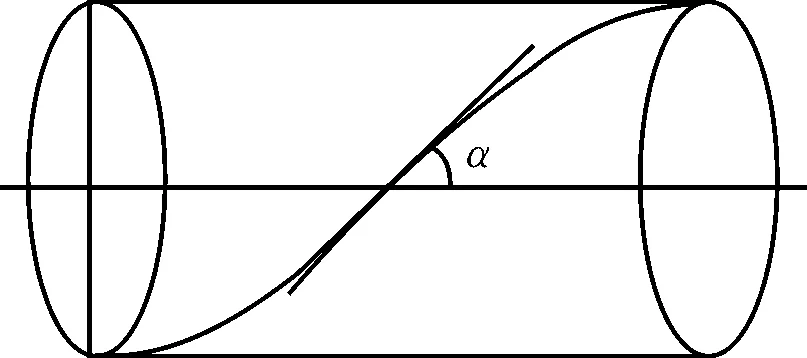
图2 螺旋扁带缠绕角
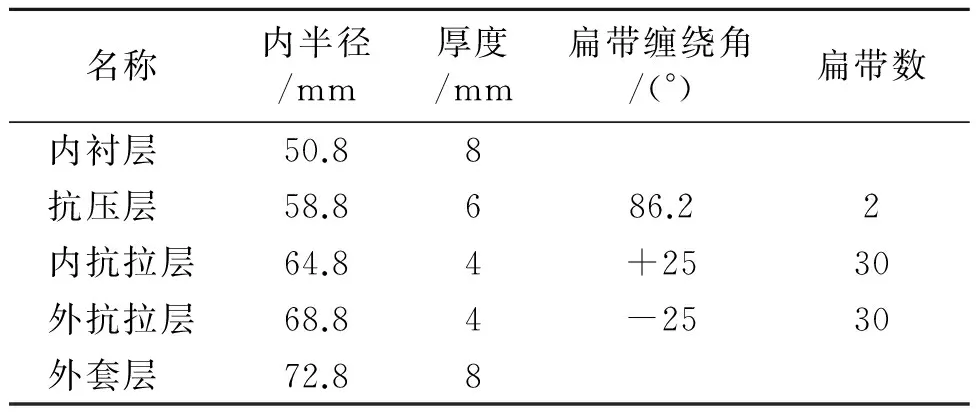
名称内半径/mm厚度/mm扁带缠绕角/(°)扁带数内衬层 50.88抗压层 58.8686.22内抗拉层64.84+2530外抗拉层68.84-2530外套层 72.88

表2 材料参数
ABAQUS是一款多功能的有限元数值模拟软件,能够解决很多复杂的工程实际问题,适用于本文中提及的非金属非粘结软管的接触问题,这是一个十分复杂的非线性问题。
使用ABAQUS软件对上述软管进行有限元数值模拟,模型长度取螺旋扁带的2倍导程,取值为1.86 m[15],导程计算公式如下。
L=(2πRi·cotαi)max
(1)
式中:Ri为扁带层内半径;αi为螺旋缠绕角度。
有限元模型的外套层和内衬层所用材料属于各向同性,而螺旋扁带层所用材料属于正交各向异性,但可以把它看成横观各向同性体,认为横向面是各向同性面。
该模型各层之间、扁带之间均存在摩擦接触问题,允许相互滑动。由于有大量的接触面,采用显示动力求解器,将稳定时间增量控制在Δtstable=3.0×10-7s范围内,分析步时间设为0.08 s,保证最后的结果中动能和内能的比值维持在3%以内,这样便能够较为准确地模拟一个准静态加载过程。采用显式算法计算模型各层之间、扁带之间的接触问题,为了更逼真地模拟接触面之间的相互作用关系,接触面法向采用硬接触,可以分开。库伦摩擦系数根据GB10006—88实验得到,且PA11与玻璃钢之间,玻璃钢与玻璃钢之间摩擦系数接近,故取较小保守值μ=0.2。
在软管模型两端的横截面中心取2个参考点,并将它们同管两端的横截面刚性连接,使得截面的运动与参考点的运动相联系起来,所有的边界条件与荷载都将施加在相应的参考点上。该模型将软管的一端设为固定端,另一端设为自由端,为了防止软管发生绕纵轴的旋转运动,限制自由端绕纵轴的自由度。在自由端施加Ft=300 kN的管轴向拉力,为了更真实地模拟准静态加载过程、方便控制加载速率,采用比较平滑的加载曲线[16],见图3,荷载时程表达式如下。
Ft=3.0×105ξ3(10-15ξ+6ξ2)
(2)

(3)
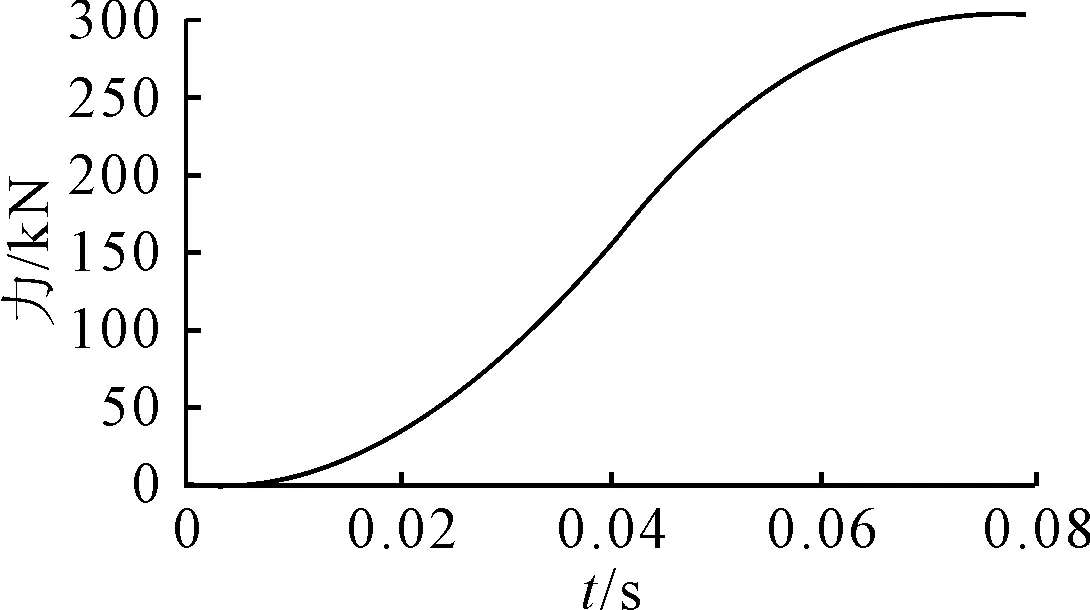
图3 加载时程曲线
由于考虑最一般的情形,不采用任何假设,因此软管模型各层全部采用8节点线性6面体单元,为了保证计算精度,需要有足够密的网格,本文模型的单元数量为152 536。为了避免数值模拟过程中“沙漏”(hourglass)带来的问题,ABAQUS引入“沙漏刚度”来限制沙漏模式的扩展,这种方法对单元多的模型十分有效。本模型的沙漏控制参数设置为stiffness[16-17],通过初步计算可以得到沙漏能与内能的比值总是小于5%,可见该模型基本可以解决沙漏问题。
非金属非粘结软管的数值模拟是一个比较复杂的问题,尤其是摩擦接触中存在的诸多非线性问题,因此其建模比较复杂,需要考虑的因素很多。采用上述设置参数可以在较短的计算时间内得到较高精度的计算结果,统筹兼顾计算效率和计算精度。
1.2 解析模型
对于在拉伸荷载作用下的非粘结软管,岳前进等提出了一种解析模型,并且给出了拉伸刚度的解析解,其通过该解析模型对一实际软管进行了计算分析,并得到了模型试验的验证,因此认为该解析方法是切实可行的。
该解析方法认为,软管的抗拉层在拉伸荷载作用下起主要的承拉作用,外套层和内衬层也能提供一定的轴向刚度,但是抗压层只起径向支撑作用。由于抗压层扁带缠绕角为90°,因此其轴向刚度可以忽略不计,并假设如下:①各层轴向变形一样;②材料是线弹性的;③各层之间无缝隙;④缠绕角的变化忽略不计;⑤拉伸过程中软管的变形和位移非常小;⑥摩擦接触忽略不计;⑦抗拉层扁带只考虑轴向变形。
岳前进等提出的受拉非粘结软管拉伸刚度的解析表达式如下。

(4)
(5)
(6)

(7)

(8)
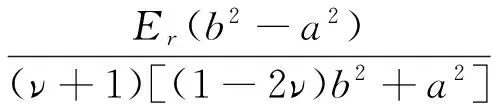
(9)
式中:EI、EO分别为内衬层和外套层的弹性模量;AI、AO分别为内衬层和外套层的横截面面积;nL为抗拉层层数;Ei、Ai、αi、ni分别为第i层扁带沿扁带轴向的弹性模量、横截面面积、缠绕角度和扁带数量;Ri、ti分别为第i层的内半径和厚度;Er为抗压层扁带垂直扁带轴向的弹性模量;ν为抗压层的主泊松比;a、b分别为抗压层的内、外半径。
1.3 2种模型结果比较与误差分析
图4为ABAQUS软件求得的非金属非粘结软管拉力-应变关系。
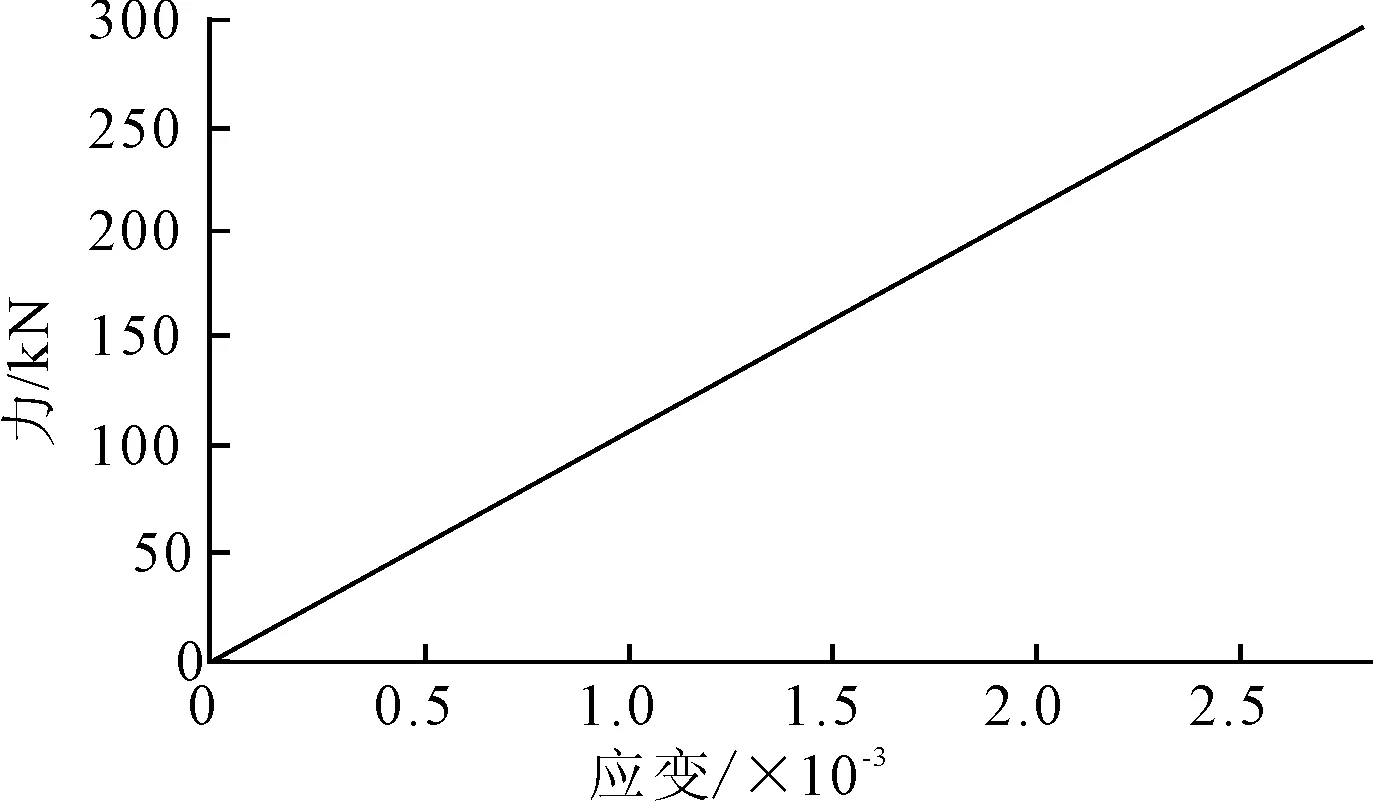
图4 ABAQUS求得的软管拉力-应变关系
(Kt)abaqus=107 719 928 N。
将软管的几何尺寸数据和工程弹性常数代入式(4)~(9),可以求得拉伸刚度的解析解:
(Kt)analytical=92 158 867 N。
因此,本文所建立的有限元数值模型与现有的解析模型之间的误差为
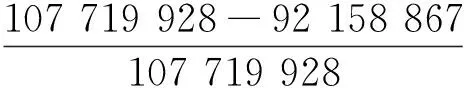
与解析法相比,ABAQUS软件的计算结果偏大,这是因为解析法引入了大量的假设。
1)忽略抗压层的抗拉作用,认为其只提供径向刚度。
2)认为抗拉层扁带缠绕角在拉伸过程中始终不变,但实际上是有所减小的。
3)认为抗拉层引起的径向压力完全由抗压层承担,这会导致抗压层所受压力偏大,导致径向刚度偏大,最终使得计算所得的拉伸刚度偏小。
以上3点是引起解析法计算所得的拉伸刚度偏小的主要原因。由于该解析模型已通过试验验证其合理可行,可以认为本文所建立的有限元数值模型是较为合理和可靠的,其方法和计算结果可以使用推广。
2 计算结果
2.1 应力计算分析
图5、图6、图7为软管在拉伸荷载Ft=300 kN作用下抗压层的径向应力、环向应力、轴向应力分布云图。
最后,财税预算管理人员要及时了解新技术。随着信息技术的革新与发展,很多新兴的管理模式或理念,如财务共享管理中心、财务共享管理理念等,已经逐渐运用到财税管理的工作中,如果财务人员不能及时转变观念,掌握一些新的财务理念和技术,那么就不能对各类财务数据资源进行整合与分析,也无法得出科学准确的预算结果。

图5 抗压层径向应力分布云图

图6 抗压层环向应力分布云图

图7 抗压层轴向应力分布云图
抗压层径向应力为负值,说明径向受压,最大压应力为2.3 MPa;环向也表现为受压状态,压应力在23.2~25.7 MPa之间;轴向应力有正有负,最大拉应力为0.5 MPa,最大压应力为1.3 MPa,可见环向应力远大于径向应力和轴向应力。分析数据可得,软管在拉伸荷载作用下,抗压层的主要承载方式是环向受压,这是由于扁带的螺旋缠绕角接近90°,径向也表现为受压状态,压力来自于抗拉层。轴向应力较小,但是同时存在拉应力和压应力,这是由于软管受拉时抗压层扁带间相互挤压,故拉应力和压应力同时存在。因此,提高抗压层扁带的环向强度能有效提高软管的抗拉性能,扁带径向强度也会影响软管的抗拉性能。同时还验证了螺旋扁带能充分利用复合材料各向异性的特点,使得玻璃钢的纵向压缩强度可以得到充分利用。
软管各层环向应力分布见图8,2层抗拉层环向应力为正,大小在15.9~19.7 MPa之间;抗压层环向应力为负,大小在23.2~25.7 MPa;内衬层和外套层的环向应力很小,低于0.4 MPa。所以软管在拉伸作用下,抗拉层环向受拉,抗压层环向受压,而外套层和内衬层应力值较小,可认为软管环向承载主要依靠抗压层受压和抗拉层受拉,内衬层和外套层没有承载作用。
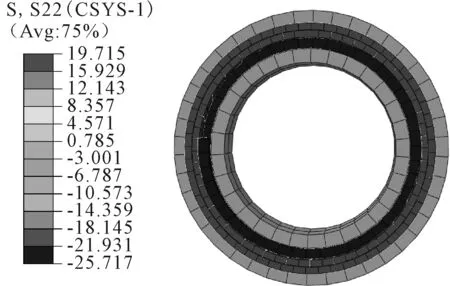
图8 软管各层环向应力分布
软管在拉伸荷载Ft=300 kN作用下内、外抗拉层的轴向应力分布见图9、10。

图9 内抗拉层轴向应力分布

图10 外抗拉层轴向应力分布
内抗拉层的最大轴向应力84.9 MPa,外抗拉层的最大轴向应力85.4 MPa,2层的轴向受力几乎相同。图11是软管各层轴向应力分布云图,内衬层和外套层应力为正,值为2.7~3.0 MPa;抗压层最大拉应力为0.5 MPa。可见软管在拉伸作用下,几乎是由内外抗拉层承受所有轴向荷载,并且内抗拉层与外抗拉层轴向受力相同。

图11 软管各层轴向应力分布
通过图8、图11可见,提高抗拉层的轴向拉伸强度和环向拉伸强度,可以提高软管的抗拉性能,即提高玻璃钢扁带沿纤维方向上的纵向拉伸强度和垂直于纤维方向的横向拉伸强度,都有利于软管拉伸性能的提高。
2.2 拉伸刚度影响参数分析
本节同样利用ABAQUS软件进行数值模拟分析,并采用上述软管的所有参数与设置,依据单因子变量法,分别改变抗拉层扁带螺旋缠绕角、抗拉层厚度、抗拉层扁带数量以及摩擦系数,还考察了不同内外压作用下的拉伸刚度。依据计算结果分别给出了软管拉力和应变关系图,得出各影响参数对拉伸刚度的影响,拉力和应变关系式如下。
F=Kt·ε
(10)
2.2.1 内外压影响分析
对软管施加轴向拉力F=300 kN,同时对软管分别施加不同的内压和外压pint=0、3、5、7 MPa,pext=0、0.2、0.4、0.6 MPa,分别进行有限元计算,最终得出自由端的拉力-应变关系,见图12、13。由图12、13可见,内外压作用下软管的拉伸刚度有所增加,但不同内外压作用下,软管的拉伸刚度变化并不明显,可认为内外压对软管拉伸刚度的影响较小。
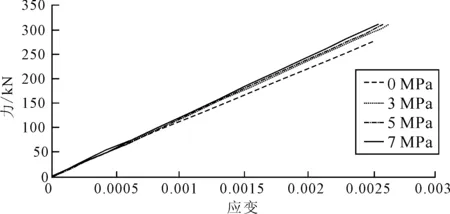
图12 不同内压作用下软管拉力-应变关系
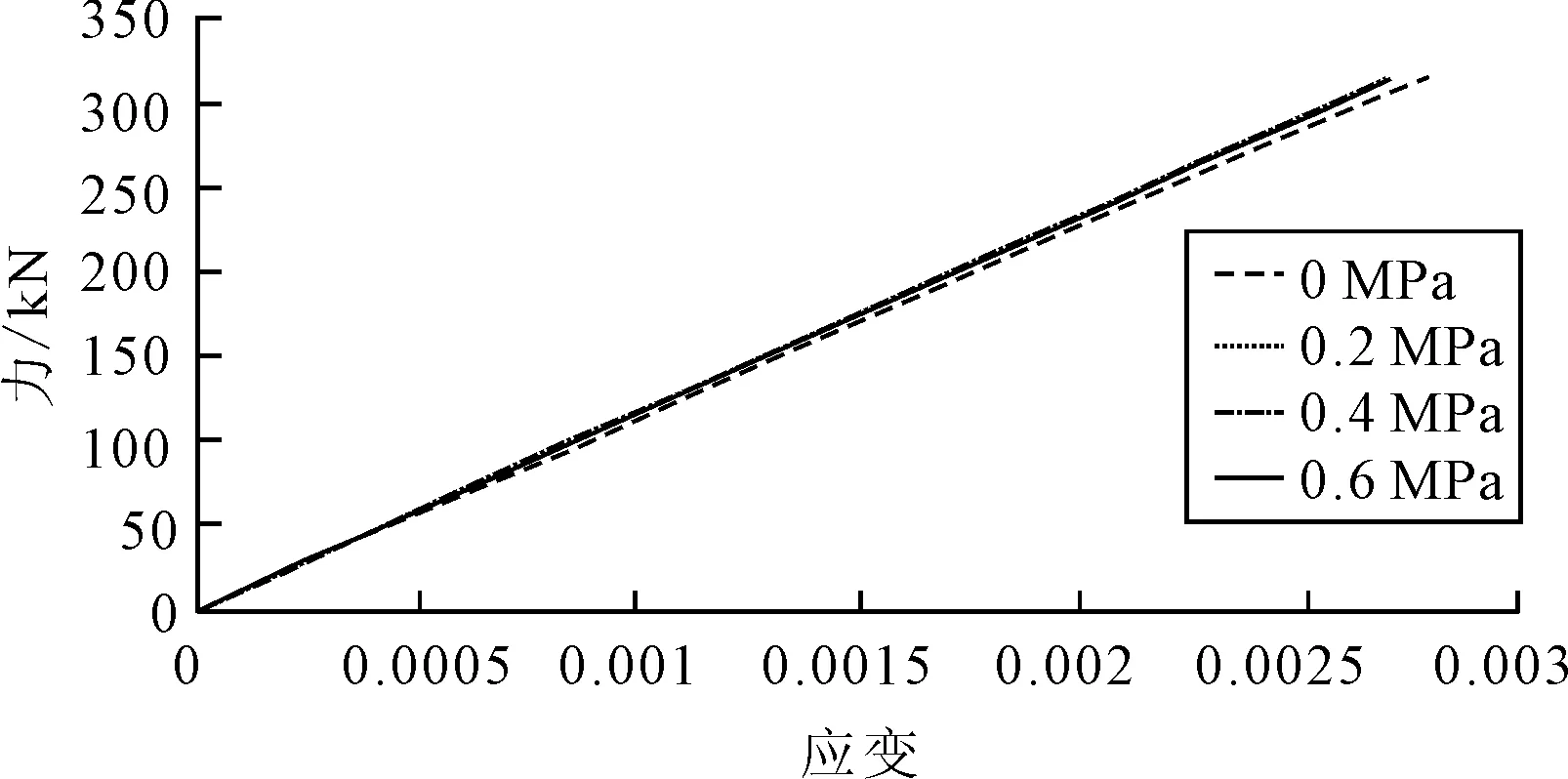
图13 不同外压作用下软管拉力-应变关系
2.2.2 抗拉层扁带数量影响分析
为了研究抗拉层扁带数量对软管拉伸刚度的影响,软管的其他参数不变,每层的扁带数分别设置为26,28,30,32,计算并绘制每个类型软管所对应的自由端拉力-应变关系图,见图14。可见软管在拉伸荷载作用下,扁带数量的变化,对拉伸刚度影响不大,故可以忽略扁带数量对拉伸刚度的影响。
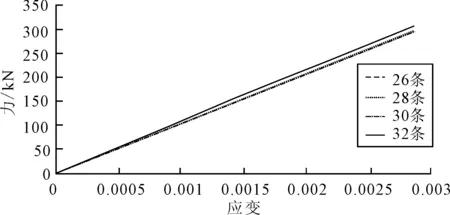
图14 抗拉层不同扁带数量下拉力-应变关系
2.2.3 抗拉层螺旋缠绕角度影响分析
API规范中建议抗拉层的螺旋缠绕角度为20°~55°,现将抗拉层的螺旋缠绕角度分别设为25°、35°、45°、55°,进行有限元计算,拉力-应变关系见图15。由图可知,软管在拉伸荷载作用下,抗拉层的螺旋缠绕角对软管拉伸刚度影响较大,随着缠绕角度的增大,拉伸刚度明显减小。因此降低抗拉层螺旋缠绕角可以大幅度地提高软管拉伸刚度。

图15 抗拉层不同缠绕角下拉力-应变关系
2.2.4 摩擦系数影响分析
软管的其他参数仍旧不变,将摩擦系数分别设为0.05、0.10、0.15、0.20进行计算,最终得到的拉力-应变关系图见图16。可见不同摩擦系数下的拉力-应变图几乎一致,故认为摩擦系数对软管拉伸刚度的影响可以忽略不计。

图16 不同摩擦系数下拉力-应变关系
2.2.5 抗拉层厚度影响分析
API规范建议抗拉层厚度不超过8 mm,现将抗拉层的厚度分别设为2,3,4,5 mm,进行有限元计算。图17为对应的拉力-应变关系图,由图可知,软管在拉伸荷载作用下,其拉伸刚度受抗拉层厚度影响较大,随着抗拉层厚度的增加,拉伸刚度也随之增加。可见增加抗拉层厚度可以有效提高软管的拉伸刚度。

图17 抗拉层不同厚度下拉力-应变关系
3 结论
1)抗压层的主要承载方式是环向受压,提高抗压层扁带的环向强度能提高软管的抗拉性能,而在沿软管环向方向上,外套层和内衬层几乎没有承载作用;内、外抗拉层几乎承受所有轴向荷载,沿环向方向也表现为受拉状态,提高抗拉层扁带的轴向拉伸强度和环向拉伸强度,可以提高软管的抗拉性能。
2)受内外压作用时,软管的拉伸刚度有所增加,但在不同内外压作用下,软管的拉伸刚度变化不明显,认为内外压对软管拉伸刚度的影响较小。降低抗拉层螺旋缠绕角、增加抗拉层厚度,都可以大幅度提高软管的拉伸刚度,而抗拉层扁带数量、摩擦系数对拉伸刚度的影响可以忽略不计。
3)非金属非粘结软管的抗拉性能主要与抗拉层有关,但与抗压层也有一定关系,其中抗拉层的螺旋缠绕角、厚度对软管的拉伸刚度有显著影响,这对将来非金属非粘结软管的实际应用有重要参考价值。
海洋软管的实际受力除了拉伸,还包括弯曲、扭转、轴向受压以及组合等多种情况。在以后的研究中,还应考虑这些受力情况,在必要时可以加入相应的物理模型实验进行验证。
[1] KEBADZE E. Theoretical modeling of unbonded flexible pipe cross-sections[D]. London, UK.: South Bank University,2000.
[2] RAMOS Jr R, PESCE C P, MARTINS C A. A comparative analysis between analytical and fe-based models for flexible pipes subjected to axisymmetric loads[C]. Seattle, USA.: Proc. of 10th 2000 Int. Offshore and Polar Eng. Conference, ISOPE,May 28-June 2,2000.
[3] RAMOS J R, PESCE C P. A consistent analytical model to predict the structural behavior of flexible risers subjected to combined loads[J]. Offshore mech. arct. eng.,2004,126:141-146.
[4] ELTON J B, JOSE R M, GILBERTO B, et al. On the tension-compression behaviors of flexible risers[C]. Proceedings of ISOPE,2003.
[5] KRAINCANIC I, KEBADZE E. Slip initiation and progression in helical armoring layers of unbonded flexible pipes and its effect on pipe bending behavior[J]. Journal of strain analysis for engineering design,2001,236:265-275.
[6] BAHTUI A, BAHAI H, ALFANO G. A finite element analysis for unbonded flexible risers under torsion[J].Offshore mech. arct. eng.,2008,130(4):1-4.
[7] BAHTUI A, BAHAI H, ALFANO G. Numerical and analytical simulation of unbonded flexible risers subjected to combined modes of loading[C]. San Fran-cisco, USA: Ninth US National Congress on Computational Mechanics,2007.
[8] BAHTUI A, BAHAI H, ALFANO G. A finite element analysis for unbonded flexible risers under axial tension[C]. Estoril, Portugal: Proceedings of the OMAE2008 27th International Conference on Offshore Mechanics and Arctic Engineering, Jun.15-20,2008.
[9] BAHTUI A, BAHAI H, ALFNO G. Constitutive modeling of un-bonded flexible risers under tension[C]. Venice, Italy:Eighth World Congress on Computational Mechanics,Jun.30-Jul. 5,2008.
[10] YUE Qianjin, LU Qingzhen, YAN Jun, et al. Tension behavior prediction of flexible pipelines in shallow water[J]. Ocean engineering,2013,58:201-207.
[11] 肖少洋.海洋柔性管道拉弯组合疲劳试验机设计研究[D].大连:大连理工大学,2016.
[12] 宫治鹏.海洋柔性管缆水下浮力模块的设计研究[D].大连:大连理工大学,2016.
[13] 曹淑刚,黄维平,周阳,等.并列双立管涡激振动特性的数值和实验研究[J].船海工程,2015,44(2):130-135.
[14] 安世居,杨强,白海洋,等.柔性软管弯曲限制器的设计[J].油气储运,2016,35(5):551-554.
[15] ANSI/API RECOMMENDED PRACTICE 17B, Recommended Practice for Flexible Pipe[S].2008.
[16] Abaqus Analysis User′s Manual[Z]. USA:Version 6.10,2010.
[17] Abaqus Keywords Reference Manual[Z]. USA: Version 6.10,2010.
Numerical Simulation of Mechanical Property of Un-bonded Flexible Fiber Reinforced Pipe under Tension
ZHOUYang1,HUANGWei-ping2,ZHANGYan-jun2,YULiang-liang1
(1.Key Laboratory of Engineering Oceanography, The Second Institute of Oceanography, SOA, Hangzhou 310012, China; 2.Shandong Key Laboratory of Ocean Engineering, Ocean University of China, Qingdao Shandong 266100, China)
In order to study the mechanical property of un-bonded flexible fiber reinforced pipe (FFRP) under tension, a detailed finite-element analysis (FEA) of un-bonded FFRP was presented in ABAQUS considering the frictional contact between all layers. It was shown that the tensile property of the flexible pipe can be enhanced when the hoop strength of compression resistance armor layer, the tensile strength and hoop tensile strength of tension resistance armor layer are enhanced. The lay angle and the thickness of tension resistance armor layer have a great influence on the tension stiffness of the flexible pipe, while the influence of internal and external pressure, tendon number of tension resistance armor layer and friction coefficient is little.
un-bonded flexible fiber reinforced pipe; FEA; frictional contact; ABAQUS; tension stiffness
P754;TV756.2
A
1671-7953(2017)06-0136-06
10.3963/j.issn.1671-7953.2017.06.031
2017-03-17
2017-04-21
国家高技术研究发展计划(863计划)(2013AA09A218);国家自然科学基金(51179179、51239008)
周阳(1987—),男,博士,工程师
研究方向:海洋结构物设计及海洋立管的涡激振动
