融合内外场退化数据的可靠性评估方法

吴晓辉, 蔡忠义, 李全祥

(1.中国飞行试验研究院,陕西 西安 710089; 2.空军工程大学 装备管理与安全工程学院,陕西 西安 710051)

融合内外场退化数据的可靠性评估方法

吴晓辉1, 蔡忠义2, 李全祥1

(1.中国飞行试验研究院,陕西 西安 710089; 2.空军工程大学 装备管理与安全工程学院,陕西 西安 710051)

针对性能退化过程服从Wiener过程的产品,文章运用贝叶斯统计推断法,提出了一种融合内场加速退化试验(accelerated degradation test,ADT)与外场退化信息的可靠性评估方法。考虑到内外场应力环境差异,提出了基于修正系数的Wiener过程双参数修正模型;建立了退化数据模型,得到各应力下分布参数估计值;将各加速应力下分布参数估计值折算到正常工作应力下,构成未知参数先验分布的数据样本;构建了外场退化数据下未知参数的后验分布函数,采用马尔科夫链蒙特卡洛(Markov chain Monte Carlo,MCMC)方法,得到参数的后验分布均值。实例分析结果验证了该文方法的正确性。

Wiener过程;退化数据融合;贝叶斯推断;应力环境差异

0 引 言

高可靠产品在外场正常工作应力环境下很难获取足够多的失效数据,导致传统基于寿命数据的评估方法不能适用,但在外场通过测量产品关键性能参数随时间的变化情况,收集外场退化信息,可以外推出产品寿命与可靠性水平[1]。同时,为了丰富产品退化数据样本、提高评估精度,可以借助于同类产品在加速退化试验(accelerated degradation test,ADT)中的性能退化数据,但是从实验室收集到的数据与外场实测数据之间存在一定的差异。若将产品外场退化信息与同类产品ADT退化信息进行融合评估,则需解决如下问题:

(1) 考虑外场与实验室之间的应力环境差异[2]。文献[2]在产品退化过程服从Wiener过程的场合下,提出了基于广义加速模型的退化过程参数修正模型来度量外场与实验室之间的应力环境差异。

(2) ADT中同类产品个体之间的退化差异[3-8]。文献[5]对Wiener过程的双系数都进行了随机化处理,假定了扩散系数服从逆伽玛分布的前提下漂移系数服从正态分布,但假定的分布类型未经分布假设检验,可能出现与实际退化数据拟合不一致的情况;文献[7]认为个体退化速率之间的差异主要在于漂移系数,仅将Wiener过程的漂移系数看作服从正态分布的随机变量,计算相对简便,但是忽略了扩散系数对性能退化的影响。

(3) ADT与外场退化信息之间的融合方法。这类研究的主要解决方法是采用贝叶斯方法对多源信息进行统计推断,建立未知参数的估计模型,运用最大期望法(expectation maximization,EM)[9-10]或马尔科夫链蒙特卡洛(Markov chain Monte Carlo,MCMC)方法[11],得到未知参数估计值。如文献[10]采用加速因子,将加速应力下样本数据折算到正常工作应力下,并以此推断出未知参数的先验分布并加以检验,使得未知参数先验分布具有良好的拟合适应性。

因此,本文针对退化过程服从Wiener过程的产品,提出了融合ADT信息与外场退化信息的评估方法。首先,提出考虑外场差异的分布参数修正模型;其次,分别建立了步进ADT数据与外场退化数据模型及分布参数估计函数;然后,确定了未知参数的先验分布,建立了未知参数后验分布函数;最后,通过实例分析验证了该方法的正确性。

1 考虑外场差异的Wiener模型

假设产品在t时刻的性能退化量为X(t),X(t)为一元连续随机过程且服从Wiener过程,可记为:

X(t)=μt+σB(t)+x0

(1)

其中,μ为漂移系数;σ为扩散系数;B(t)为标准布朗运动;x0为性能退化初值。

对于加速试验,一般认为Wiener过程的漂移系数μ与应力S(本文应力只讨论大小)有关,而扩散系数σ与S无关,则加速模型一般可以表示为:

μ=exp[a+bφ(S)]

(2)

其中,a、b为待定常数;φ(S)为S的函数。

与内场(实验室)应力环境相比,产品在外场工作环境所发生的失效机理更加复杂,通常是由多方面应力共同作用而出现的。因此,对于外场工作环境中产品分布模型的参数进行一定的修正,则有:

μf=μAk1

(3)

其中,k1、k2为修正系数;μf、μA为外场和试验应力环境下的漂移系数;σf、σA为外场和试验应力环境下的扩散系数。

经推导可知,首次达到l时的寿命服从逆高斯分布,则外场应力环境下产品的可靠度、概率密度函数分别为:

2 退化数据建模

(1) 步进加速退化数据。现有m个试样在n个加速应力下进行步进ADT。由于每个新应力下的退化量初值等于上一步应力下的退化量末值,则步进ADT中各应力下的性能退化量可表示为:

X(t)=

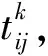
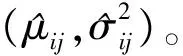
(2) 外场退化数据。对于外场应力环境下的某待估产品,通过测量得到该产品的性能退化数据Xf,其表达式如下:

Xf=[Xf(t1),Xf(t2),…,Xf(tK′)]，

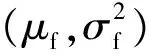
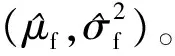
3 贝叶斯参数估计

采用贝叶斯方法,以外场实测的性能退化数据Xf为评估对象,建立似然估计函数;将ADT退化信息作为先验信息,推断出参数集Θ的先验分布类型及其超参数估计,表达式如下:

π(Θ|Xf)∝L(Xf|Θ)f(Θ)

(10)

其中,π(Θ|Xf)为待估参数集Θ的后验分布函数;L(Xf|Θ)为似然估计函数;f(Θ)为先验分布函数。

3.1 参数先验分布确定

(1) 确定先验分布的类型。由文献[11]推导出的加速应力与Wiener过程参数之间的关系可知,加速因子Apq与漂移系数、扩散系数之间满足如下关系式:

将(2)式代入(11)式可知:

Apq=exp{b[φ(Sp)-φ(Sq)]}

(12)

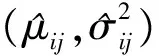
(2) 确定先验分布的超参数估计。确定参数的先验分布类型后,可得各参数的先验分布密度函数,建立似然估计函数,估计出先验分布密度函数中的未知超参数。

3.2 参数后验分布确定

确定所有待估参数的先验分布后,由(10)式可知,外场退化数据Xf下参数集Θ的后验分布形式为:

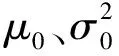
4 实例分析

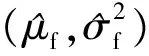
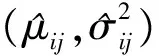
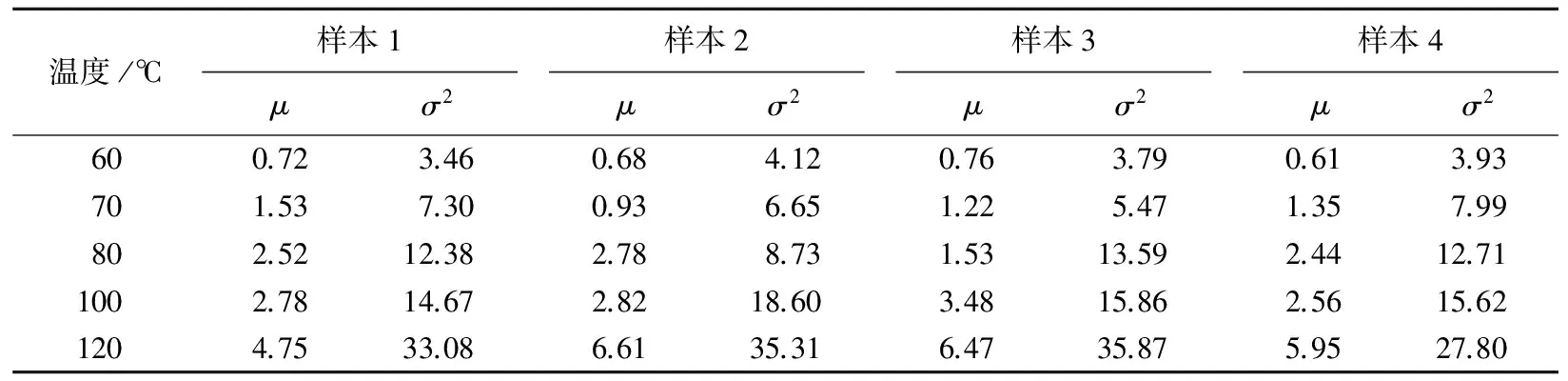
表1 ADT应力下分布参数的估计值 10-4

表2 ADT应力下分布参数估计值折算到正常应力下的估计值 10-4

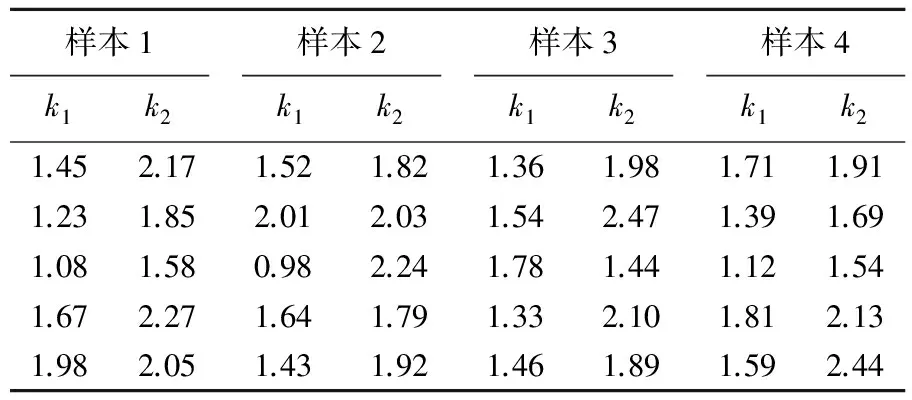
表3 外场修正系数k1、k2的数据样本

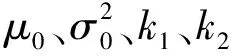
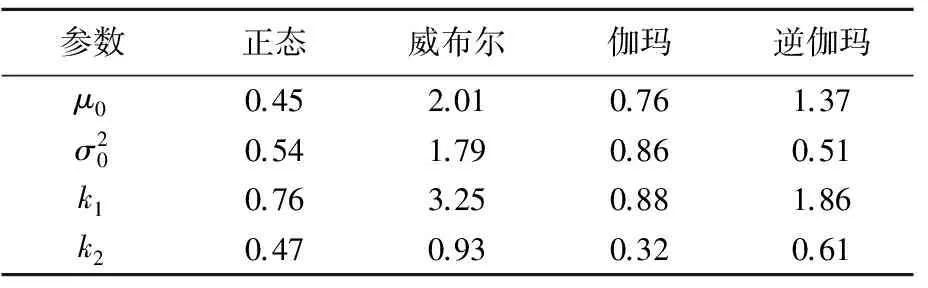
表4 备选分布下参数的检验统计量

k2～Γ(ak2,bk2)=Γ(49.15,24.95)。

(3) 参数后验分布确定。根据(14)式和求得的未知参数分布模型,采用WinBUGS软件对上式进行基于Gibbs抽样的MCMC仿真计算,得到马尔科夫链收敛时的参数集Θ后验均值。同时,根据待估产品外场退化数据情况,估计出不同采样次数t下参数后验均值并与文献[2]中的参数真值进行比较,结果见表5所列。

表5 不同采样次数下参数后验均值

由表5可知,随着外场采样退化数据的不断丰富,融合先验ADT与外场退化数据的参数后验均值越接近于真实值,估计精度越高。

(4) 评估结果分析。将本文采用贝叶斯方法来融合ADT与外场退化数据的评估方法记为M1,将只利用外场退化数据的评估方法记为M2。将两者得到的参数Θ后验均值代入(9)式、(10)式,得到产品在外场工作环境下的分布参数估计值,见表6所列。

表6 外场环境下不同方法的分布参数估计

将表6中的外场应力环境下的分布参数估计值代入(5)式、(6)式,得到M1的可靠度,并与M2值、真值进行对比,结果如图1所示。

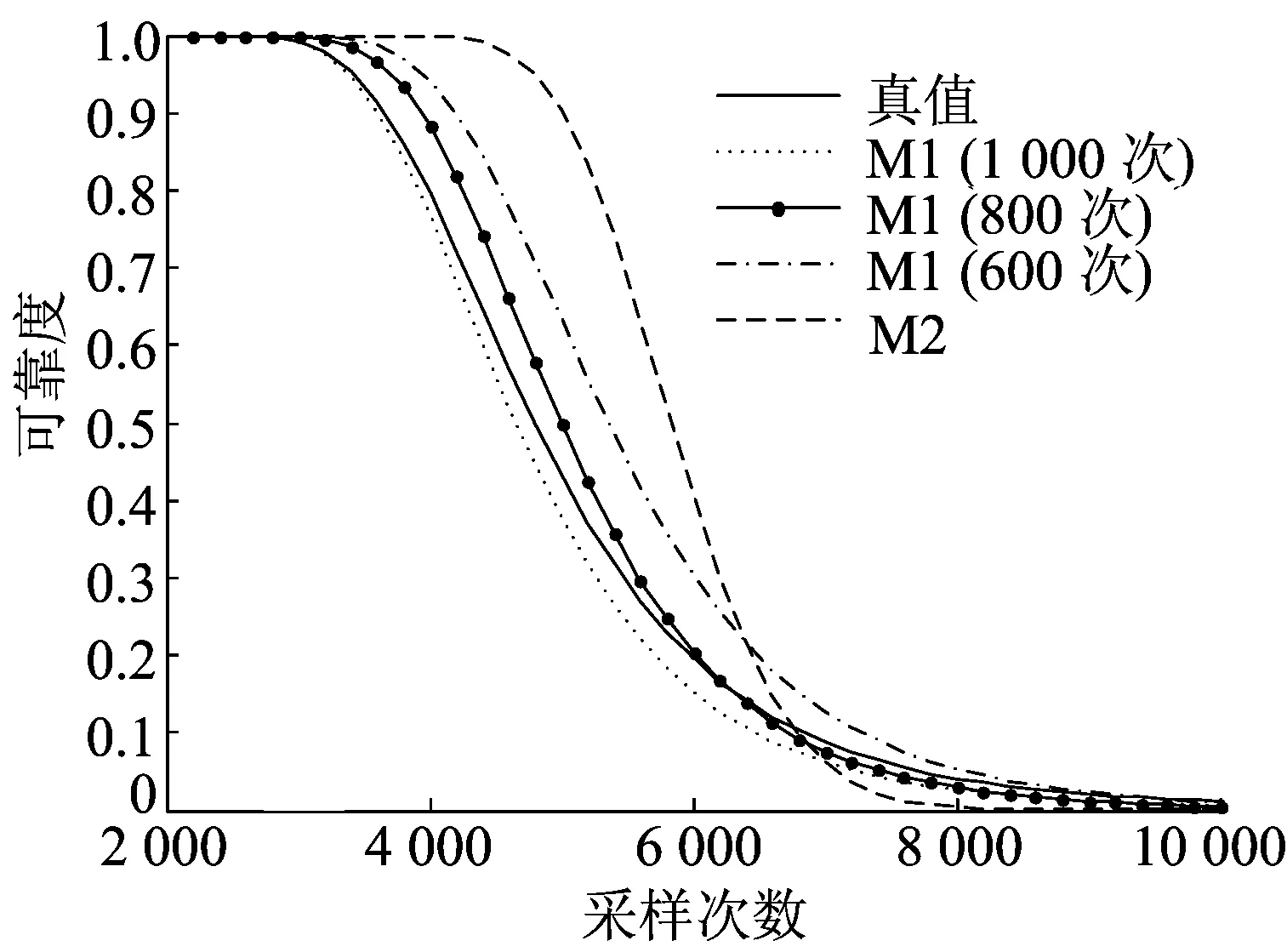
图1 不同方法的可靠度曲线

由图1可以看出:① M1与真值之间的拟合程度要明显优于M2与真值之间的拟合程度;② 随着外场采样次数的不断增多,M1拟合曲线逐渐向真值曲线接近。这是由于M1采用贝叶斯方法,对ADT与外场信息进行了融合处理,将ADT信息作为参数估计的先验信息,使得参数的后验估计值与真值更加接近,且随着外场信息的不断充实,参数后验估计值不断接近真值,产品外场可靠性评估结果也不断接近外场实际水平。

5 结 论

(1) 本文考虑到外场与内场之间的应力环境差异,提出了基于修正系数的Wiener过程双参数修正模型,从总体上对同类产品ADT下分布参数进行修正。

(2) 考虑到同类产品个体之间的退化差异,将Wiener过程参数进行随机化处理,利用加速因子,将各加速应力下分布参数估计值折算到正常工作应力下,构成未知参数先验分布的数据样本;采用CvM检验法,从备选分布中确定未知参数最优的先验分布类型。

(3) 采用MCMC法,仿真得到未知参数集的后验分布均值,并通过不断丰富外场采样数据来及时更新后验分布均值,实现产品外场可靠性的实时评估。

[1] 姜同敏.可靠性试验技术[M].北京:北京航空航天大学出版社,2012.

[2] 王立志,姜同敏,李晓阳,等.融合加速试验及外场使用信息的寿命评估方法[J].北京航空航天大学学报,2013,39(7):947-951.

[3] WHITMORE G A.Normal-gamma mixtures of inverse Gaussian distribution [J].Scandinavian Journal of Statistics,1986,13(1):211-220.

[4] WANG X.Wiener processes with random effects for degradation data [J].Journal of Multivariate Analysis,2010,101(2):340-351.

[5] 王小林,郭波,程志君.融合多源信息的维纳过程性能退化产品的可靠性评估[J].电子学报,2012,40(5):977-982.

[6] PENG C Y,TSENG S T.Mis-specification analysis of linear degradation models [J].IEEE Transactions on Reliability,2009,58(3):444-455.

[7] 唐圣金,郭晓松,周召发,等.步进应力加速退化试验的建模与剩余寿命估计[J].机械工程学报,2014,50(16):33-40.

[8] TANG S J,YU C Q,WANG X,et al.Remaining useful life prediction of lithium-ion batteries based on the Wiener process with measurement error [J].Energies,2014,7(2):520-547.

[9] 彭宝华,周经论,孙权,等.基于退化与寿命数据融合的产品剩余寿命预测[J].系统工程与电子技术,2011,33(5):1073-1078.

[10] 徐廷学,王浩伟,张鑫.EM算法在Wiener 过程随机参数的超参数估计中的应用[J].系统工程与电子技术,2015,37(3):707-712.

[11] 王浩伟,徐廷学,赵建忠.融合加速退化和现场实测退化数据的剩余寿命预测方法[J].航空学报,2014,35(12):3350-3357.

Reliabilityassessmentmethodwithintegrationofinfieldandoutfielddegradationdata

WU Xiaohui1, CAI Zhongyi2, LI Quanxiang1

(1.Chinese Flight Test Establishment, Xi’an 710089, China; 2.College of Equipment Management and Safety Engineering, Air Force Engineering University, Xi’an 710051, China)

Aiming at the degradation process of products which obeys Wiener process, reliability assessment method with accelerated degradation test(ADT) data and field degradation data is put forward by using Bayesian statistical inference. Given the difference between field and laboratory stress environment, Wiener process double-parameters modified model with the correction factors is constructed. Degradation model is built to obtain estimated values of distribution parameters under each stress. Estimated values under accelerated stress are converted into those under regular stress, which constitute the data sample of prior distribution of unknown parameters. Posterior distribution function of unknown parameters under field degradation data is built and Markov chain Monte Carlo(MCMC) method is used to obtain mean values of posterior distribution. The accuracy and practical applicability of the presented method is verified by an example.

Wiener process; degradation data integration; Bayesian inference; stress environment difference

2016-06-07；

2016-10-17

国家自然科学基金资助项目(71601183);陕西省自然科学基金资助项目(2014JQ2-7045)

吴晓辉(1981-),男,陕西咸阳人,中国飞行试验研究院高级工程师.

10.3969/j.issn.1003-5060.2017.12.002

TB114.3

A

1003-5060(2017)12-1589-05

文献[2]中的数据,根据其所提出的评估方法,融合先验ADT与外场退化信息,对待估产品外场寿命与可靠性进行评估,具体分析如下:

(责任编辑胡亚敏)