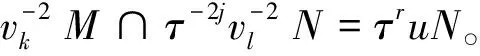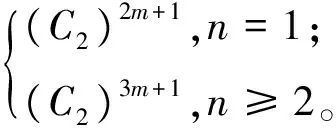广义二面体群的Burnside环之增广商群

温亚男, 常 山

(合肥工业大学 数学学院, 安徽 合肥 230009)

广义二面体群的Burnside环之增广商群

温亚男, 常 山

(合肥工业大学 数学学院, 安徽 合肥 230009)

设H是具有循环Sylow 2-子群的有限交换群,D是H的广义二面体群。记D的Burnside环为Ω(D),Ω(D)的增广理想为Δ(D)。文章对任意正整数n,具体构造了Δn(D)作为自由交换群的一组基,并确定了商群Δn(D)/Δn+1(D)的结构, 其中Δn(D)表示Δ(D)的n次幂。

广义二面体群;Burnside环;增广理想;增广商群

0 引 言

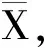
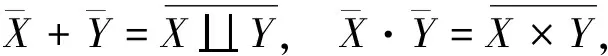
设H是具有循环Sylow2-子群的有限交换群,D是H的广义二面体群。本文对任意正整数n, 具体构造了Δn(D)作为自由交换群的一组基, 并确定了Qn(D)的结构。

1 预备知识

本文列出Ω(G)、Δn(G)、Qn(G)以及自由交换群的若干基本性质。

设X是G-集,x,y∈X。若存在g∈G,使得gx=y,则称x与y相关。易见相关关系是X上的等价关系, 其等价类称为轨道, 显然x所在的轨道为Gx={gx|g∈G}。若X只有一个轨道, 则称X是传递G-集。显然x所在的轨道Gx本身是一个传递G-集。此外, 若K是G的子群, 则K的左陪集类G/K在作用g(hK)=(gh)K下也是一个传递G-集。

引理1[1]设X是传递G-集,x∈X,则

Gx≅G/Gx,

其中,Gx={g∈G|gx=x}是x的稳定子群。

引理2[1]设K、L是G的子群, 则G/K≅G/L当且仅当K与L在G中共轭,记作K～L。

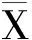
其中,dK为X中同构于G/K的轨道的个数。

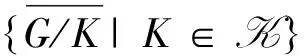
由计算可知,|#(G/G)|=1且对G的任意真子群K总有|#(G/K)|=0, 于是立得如下推论。

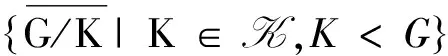
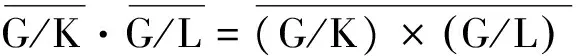
引理3[5]设K是G的子群,L是G的正规子群, 则

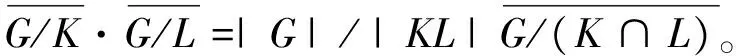
引理4[5]对任意正整数n,Δn(G)的自由秩都等于Δ(G)的自由秩。

最后给出一个关于自由交换群的经典结论。

引理5[16]设F是秩为r的自由交换群, 若F中有r个元可以生成F, 则这r个元构成F的一组基。

2 D的子群及其共轭类

本文确定广义二面体群的子群及其共轭类, 进而给出广义二面体群的Burnside环及其增广理想作为自由交换群的基。

设H是有限交换群,H的广义二面体群D是H与2阶循环群的半直积。具体地,D可划分为H与σH的不交并, 其中,σ为该2阶循环群的生成元;D中运算由等式σ-1hσ=h-1决定，h∈H。

引理6 设H是有限交换群,D是H的广义二面体群,K是D的子群。

(1) 若K⊆H,则K是D的正规子群。

(2) 若K⊄H,则存在h∈H,使得K=N∪σhN, 其中N=K∩H。

证明(1)由D的定义直接可得。

(2) 注意到K=N∪(K∩σH),因此仅需证明存在h∈H,使得K∩σH=σhN。

由K⊄H可知,K∩σH≠∅。于是存在h∈K,使得σh∈K∩σH, 立得σhN∈K∩σH。

另一方面,设σg∈K∩σH,其中h∈H。经计算可知,σhσg=h-1g∈K∩H=N,从而σg=σh(h-1g)∈σhN,即得K∩σH=σhN。

设H的Sylow 2-子群是2m阶循环群, 则H有直积分解H=〈τ〉×U,其中，τ的阶为2m；U为奇数阶交换群。设N是H的子群, 则N=〈τ2q〉×T,其中，0≤q≤m;T为U的子群。

引理7 设H、N如上定义,h=τru,u∈U,则在H的广义二面体群D中,有

(1)N∪σhN～N∪στrN～

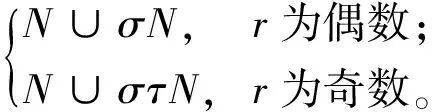
(2)N∪σN～N∪στN当且仅当q=0。

证明(1) 注意到u是奇数阶元, 设u的阶为2i+1,经计算可得:

u-i(N∪σhN)ui=u-iNui∪u-iσhNui=

N∪σhu2iN=N∪στrN,

即得N∪σhN～N∪στrN。类似地, 对任意整数j, 经计算可得:

τj(N∪στrN)τ-j=τjNτ-j∪τjστrNτ-j=

N∪στr-2jN,

立得结论。

(2) 易见,当q=0时,τ∈N。于是τN=N, 从而N∪στN=N∪σN。反之, 假设存在g∈D,使得g-1(N∪σN)g=N∪στN,则

g-1(N∪σN)g=g-1Ng∪g-1στNg=

N∪g-1σgN。

再设g=σkτlv,其中,0≤k≤1;0≤l≤2m-1;v∈U。经计算可得:

g-1σg=(σkτlv)-1σ(σkτlv)=

v-1τ-lσ-kσσkτlv=v-1τ-lστlv=στ2lv2,

于是τ2lv2N=τN, 故τ2l-1v2∈N, 立得τ2l-1∈〈τ2q〉。 注意到,当q≥1时,〈τ2q〉中没有τ的奇数次幂, 因此必有q=0。

应用引理7可构造Ω(D)和Δ(D)作为自由交换群的一组基。为了表达简便起见, 约定如下记号:

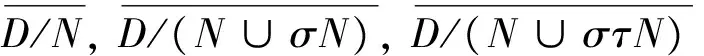
(2) 简记[q,U]0,[q,U]1,[q,U]2为[q]0,[q]1,[q]2。

(3) 对Ω(D)的任一子集Π,用ZΠ表示Π中元素的所有整系数线性组合构成的集合。

定理3 设H=〈τ〉×U, 其中,τ的阶为2m;U为奇数阶交换群。D是H的广义二面体群, 则Ω(D)在加法下是以{[q,T]0|0≤q≤m;T≤U}∪{[0,T]1|T≤U}∪{[q,T]t|1≤q≤m;T≤U;t=1,2}为基的自由交换群。

推论2 Δ(D)在加法下是以{[q,T]0|0≤q≤m;T≤U}∪{[0,T]1|T

3 Δn(D)与Qn(D)的结构

本文先证明Ω(D)中的若干乘法等式, 进而具体构造Δn(D)作为自由交换群的一组基并确定Qn(D)的结构。以下总假设H=〈τ〉×U, 其中,τ的阶为2m;U为奇数阶交换群;D为H的广义二面体群。注意到,当m=0时,H为奇数阶交换群, 此情形文献[5]已解决, 因此不妨假设m≥1。

引理8 设0≤p,q≤m,S、T是U的子群。

(1) 若p≤q,则

(2) 对t=1,2,总有

[p,S]0[q,T]t=

(3) 若p≤q,则对任意s,t∈{1,2},总有

[p,S]s[q,T]t∈Z{[q,S∩T]0,

[q,S∩T]1,[q,S∩T]2}。

证明(1)、(2)是引理3的直接推论。对于(3), 这里仅证明s=t=1的情形, 其他情形类似可证。记为：

M=〈τ2p〉×S,N=〈τ2q〉×T,

易见D/(M∪σM)中的元可表示为τiu(M∪σM),D/(N∪σN)中的元可表示为τjv(N∪σN)。其中,0≤i≤2p-1;0≤j≤2q-1；u,v∈U。令

x=(τiu(M∪σM),τjv(N∪σN))∈

D/(M∪σM)×D/(N∪σN)。

经计算可得x的稳定子群如下：

Dx=(τiu(M∪σM)τ-iu-1)∩

(τjv(N∪σN)τ-jv-1)=

(M∪στ-2iu-2M)∪(N∪στ-2jv-2N)=

(M∩N)∪σ(τ-2iu-2M∩τ-2jv-2N),

从而

Dx∩H=M∩N=

(〈τ2p〉×S)∩(〈τ2p〉×T)=

(〈τ2p〉∩〈τ2p〉)×(S∩T)=〈τ2p〉×(S∩T)。

由引理6和引理7可知,x所在轨道的同构类为[q,S∩T]0、[q,S∩T]1或[q,S∩T]2,即得结论。

命题1 设0≤q≤m,T是U的子群,M=〈τ〉×T,N=〈τ2q〉×T,u,v∈U,j是任意整数,则u-2M∩τ-2jv-2N≠∅的充要条件是uT=vT。

证明经计算可得:

u-2M=u-2(〈τ〉×T)=〈τ〉×(u-2T),

τ-2jv-2N=τ-2jv-2(〈τ2q〉×T)=

(τ-2j〈τ2q〉)×(v-2T)。

于是有：

u-2M∩τ-2jv-2N=(τ-2j〈τ2q〉)×

(u-2T∩v-2T)。

因此,u-2M∩τ-2jv-2N≠∅。当且仅当u-2T∩v-2T≠∅, 即u-2T=v-2T。当uT=vT时,结论显然成立。反之, 若u-2T=v-2T, 则u2v-2∈T。注意到U是奇数阶交换群, 因此可假设uv-1的阶为2t+1, 于是

uv-1=(u2v-2)-t∈T,

即得uT=vT。

引理9 设0≤q≤m，T是U的子群,t=1,2,则

证明这里仅证明t=1的情形,t=2的情形类似可证。设

M=〈τ〉×T,N=〈τ2q〉×T,

其中vl∈U,则

D/(M∪σM)=

同理,D/(N∪σN)可表示为:

令

z=(vk(M∪σM),τjvl(N∪σN))∈

D/(M∪σM)×D/(N∪σN),

经计算可得z的稳定子群:

注意到M∩N=N=〈τ2q〉×T,若

∅,

则z所在轨道的同构类为[q,T]0。若

∅,

引理10 设1≤p,q≤m,则

[p]1[q]2=2min{p,q}-1[max{p,q}]0。

证明令

M=〈τ2p〉×U,N=〈τ2q〉×U,

易见D/(M∪σM)中的元可表示为τi(M∪σM),D/(N∪στN)中的元可表示为τj(N∪στN),其中,0≤i≤2p-1;0≤j≤2q-1。令

y=(τi(M∪σM),τj(N∪στN))∈

D/(M∪σM)×D/(N∪στN),

经计算可得y的稳定子群:

Dy=(M∩N)∪σ(τ-2iM∩τ1-2jN),

且

τ-2iM∩τ1-2jN=

τ-2i(〈τ2p〉×U)∩τ1-2j(〈τ2q〉×U)=

(τ-2i〈τ2p〉∩τ1-2j〈τ2q〉)×U。

由p≥1可知,τ-2i〈τ2p〉中全是τ的偶数次幂；由q≥1可知,τ1-2j〈τ2q〉中全是τ的奇数次幂, 因此

τ-2i〈τ2p〉∩τ1-2j〈τ2q〉=∅。

于是Dy=〈τ2max{p,q}〉×U,故y所在轨道的同构类为[max{p,q}]0。分别计算[p]1、[q]2和[max{p,q}]0的基数可知[p]1[q]2中的轨道个数恰为2max{p,q}-1, 立得结论。

引理11 设1≤p≤q≤m,t=1,2，则

[p]t[q]t=2[q]t+(2p-1-1)[q]0。

证明这里仅证明t=1的情形,t=2的情形类似可证。设M=〈τ2p〉×U,N=〈τ2q〉×U,则

D/(M∪σM)={τi(M∪σM)|0≤i≤2p-1},

D/(N∪σN)={τj(N∪σN)|0≤j≤2q-1}。

令

x=(τi(M∪σM),τj(N∪σN))∈

D/(M∪σM)×D/(N∪σN),

经计算可得x的稳定子群:

Dx=(M∩N)∩σ(τ-2iM∩τ-2jN)。

易见M∩N=N, 于是由引理9的证明可知, 如果τ-2iM∩τ-2jN=∅,那么x所在轨道同构类为[q]0, 否则为[q]1。计算可得：

τ-2iM∩τ-2jN=(τ-2i〈τ2p〉∩τ-2j〈τ2q〉)×U。

再由1≤p≤q可知:

τ-2i〈τ2p〉∩τ-2j〈τ2q〉≠∅ ⟺

〈τ2p〉∩τ2i-2j〈τ2q〉≠∅ ⟺

τ2(i-j)∈〈τ2p〉 ⟺ 2p-1|(i-j)。

因此,在D/(M∪σM)×D/(N∪σN)中,共有2p+1个元所在轨道的同构类为[q]1, 这些元恰好组成2个轨道。余下的元所在轨道的同构类均为[q]0, 计算相关D-集的基数可知,余下元组成轨道的个数恰为2p-1-1, 立得结论。

推论3 设

Λ={[q,T]0|0≤q≤m;T

{[0,T]1|T

{[q,T]t|1≤q≤m;T

则

(1) 对任意正整数n,总有Λ⊆Δn(D)。

(2)Λ·Δ(D)⊆ZΛ。

证明(1) 对n归纳。当n=1时, 由定理3的推论即得。假设n≥2且Λ⊆Δn-1(D), 由引理8可知:

[q,T]0=[0]0[q,T]1∈Δ(D)Δn-1(D)=Δn(D)。

再由引理9可知,对s=1,2,总有:

[q,T]t=[0,T]t[q,T]t-

立得Λ⊆Δn(D)。

(2) 由引理8即得。

定理4 对任意n≥2,Δn(D)在加法下是以Λ∪Γn为基的自由交换群, 其中,

Γn={2n-1[0]0}∪{2n-2[q]0|1≤q≤m}∪

{2n-1[q]t|1≤q≤m;t=1,2}。

证明由引理4和定理3的推论知,当n≥2时,Δn(D)的自由秩总是等于Λ∪Γn的基数。因此由引理5可知,仅需证明Λ∪Γn是Δn(D)的生成元集。

对n归纳。当n=2时, 由定理3的推论可知,Δ(D)在加法下是以

Λ∪{[q]0|0≤q≤m}∪

{[q]t|1≤q≤m;t=1,2}

为基的自由交换群。再应用引理8、引理10、引理11及其推论,经计算可得:

Δ2(D)=Δ(D)Δ(D)=

ZΛ+Z{[p]0[q]0|0≤p≤q≤m}+

Z{[p]0[q]t|0≤p≤m;1≤q≤m;t=1,2}+

Z{[p]t[q]t|1≤p≤q≤m;t=1,2}+

Z{[p]1[q]2|1≤p,q≤m}=

ZΛ+Z{2p+1[q]0|0≤p≤q≤m}+

Z{2min{p,q}[max{p,q}]0|0≤p≤m;

1≤q≤m}+Z{2[q]t+

(2p-1-1)[q]0|1≤p≤q≤m;t=1,2}+

Z{2min{p,q}-1[max{p,q}]0|1≤p,q≤m}=

ZΛ+Z{2[q]0|0≤q≤m}+Z{[q]0|1≤

q≤m}+Z{2[q]t+(2p-1-1)[q]0|1≤p≤

q≤m;t=1,2}+Z{[q]0|1≤q≤m}=

ZΛ+Z{2[0]0}+Z{[q]0|1≤q≤m}+

Z{2[q]t|1≤q≤m;t=1,2},

即Λ∪Γ2是Δ2(D)的生成元集。假设结论对n成立, 即Λ∪Γn是Δn(D)的生成元集, 经计算可得:

Δn+1(D)=Δ(D)Δn(D)=

ZΛ+Z{2n-1[p]0[0]0|0≤p≤m}+

Z{2n-2[p]0[q]0|0≤p≤m;1≤q≤m}+

Z{2n-1[p]0[q]t|0≤p≤m;

1≤q≤m;t=1,2}+

Z{2n-1[p]s[0]0|1≤p≤m;s=1,2}+

Z{2n-2[p]s[q]0|1≤p,q≤m;s=1,2}+

Z{2n-1[p]s[q]t|1≤p,q≤m;

s,t∈{1,2}}=

ZΛ+Z{2n[p]0|0≤p≤m}+

Z{2n+min{p,q}-1[max{p,q}]0|0≤p≤m;1≤

q≤m}+Z{2n+min{p,q}-1[max{p,q}]0|0≤p≤m;

1≤q≤m}+Z{2n[p]0|1≤p≤m}+

Z{2n+min{p,q}-2[max{p,q}]0|1≤p,q≤m}+

Z{2n-1[p]t[q]t|1≤p≤q≤m;t=1,2}+

Z{2n-1[p]1[q]2|1≤p,q≤m}=

ZΛ+Z{2n[p]0|0≤p≤m}+

Z{2n-1[q]0|1≤q≤m}+Z{2n-1[q]0|1≤

q≤m}+Z{2n-1(2[q]t+(2p-1-1)[q]0)|1≤

p≤q≤m;t=1,2}+

Z{2n+min{p,q}-2[max{p,q}]0|1≤

p,q≤m}=

ZΛ+Z{2n[0]0}+Z{2n-1[q]0|1≤

q≤m}+Z{2n[q]t|1≤q≤m;t=1,2}+

Z{2n-1[q]0|1≤q≤m}=

ZΛ+Z{2n[0]0}+Z{2n-1[q]0|1≤q≤m}+

Z{2n[q]t|1≤q≤m;t=1,2},

立得Λ∪Γn+1是Δn+1(D)的生成元集, 定理得证。

定理5 对任意正整数n,

其中,C2表示2阶循环群。

证明由定理3的推论和定理4即得。

[1] MAGURN B A.An algebraic introduction to K-theory [M].Cambridge：Cambridge University Press，2002：135-141.

[2] 武海波，唐国平.有限交换群的Burnside环的增广理想的连续商群的结构[J].数学进展，2007，36(5)：627-630.

[3] WU H B,TANG G P.The structure of powers of the augmentation ideal and their quotients for the Burnside ring of a dihedral group [J].Adv Math (China)，2017，46(3)：380-386.

[4] 武海波，唐国平.循环群的极大子群作用下的Burnside环的连续商群[J].中国科学院大学学报，2016，33(2)：302-305.

[5] CHANG S.Augmentation quotients for Burnside rings of generalized dihedral groups[J].Czechoslovak Mathematical Journal，2016，66(4)：1165-1175.

[6] TANG G H，LI Y，WU Y S.On the consecutive quotients for Burnside ring of some nonabelian 2-groups [J].广西师范学院学报(自然科学版)，2016，33(2)：1-7.

[7] PARMENTER M M.A basis for powers of the augmentation ideal[J].Algebra Colloq，2001，8(2)：121-128.

[8] TANG G P.Presenting powers of augmentation ideals of elementary p-groups [J].K-Theory，2001，23(1)：31-39.

[9] TANG G P.On a question of Karpilovsky [J].Algebra Colloq,2003，10(1)：11-16.

[10] BAK A，TANG G P.Solutions to the presentation problem for powers of the augmentation ideal of torsion free and torsion abelian groups [J].Adv Math，2004，189(1)：1-37.

[11] TANG G P.Structure of augmentation quotients of nite homocyclic abelian groups [J].Sci China Ser A，2007，50 (9)：1280-1288.

[12] CHANG S，TANG G P.A basis for augmentation quotients of nite abelian groups [J].Journal of Algebra，2011，327:466-488.

[13] CHANG S，CHEN H，TANG G P，Augmentation quotients for complex representation rings of dihedral groups [J].Front Math China，2012，7(1)：1-18.

[14] 常山.点群的复表示环之增广商群[J].安徽大学学报(自然科学版)，2014，38(4)：13-19.

[15] CHANG S，Augmentation quotients for complex representation rings of generalized quaternion groups [J].Chinese Annals of Mathematics Ser B，2016，37(4)：571-584.

[16] LANG S.Algebra [M].3 rd.New York：Springer，2005：42-46.

AugmentationquotientsforBurnsideringsofsomegeneralizeddihedralgroups

WEN Yanan, CHANG Shan

(School of Mathematics, Hefei University of Technology, Hefei 230009, China)

LetHbe a finite abelian group whose Sylow 2-subgroup is cyclic,Dbe its generalized dihedral group. Denote the Burnside ring ofDand its augmentation ideal byΩ(D) andΔ(D), respectively. This paper constructs an explicit basis ofΔn(D) as a free abelian group and determines the isomorphism class of then-th quotient groupΔn(D)/Δn+1(D) for each positive integern, whereΔn(D) is then-th power ofΔ(D).

generalized dihedral group; Burnside ring; augmentation ideal; augmentation quotient

2016-08-24；

2017-04-20

国家自然科学基金青年科学基金资助项目(11401155)；安徽省自然科学基金青年资助项目(1308085QA01)

温亚男(1993-),女,安徽淮北人,合肥工业大学硕士生;

常 山(1983-),男,安徽合肥人,博士,合肥工业大学副研究员,硕士生导师，通讯作者,Email:changshan@hfut.edu.cn.

10.3969/j.issn.1003-5060.2017.12.026

O152.1

A

1003-5060(2017)12-1719-06

(责任编辑朱晓临)